北师大版七年级数学下册第二章相交线与平行线1两条直线的位置关系 学案(含答案)
文档属性
| 名称 | 北师大版七年级数学下册第二章相交线与平行线1两条直线的位置关系 学案(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 323.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-08-26 00:00:00 | ||
图片预览



文档简介
第二章
相交线与平行线
1
两条直线的位置关系
第1课时
相交线与平行线
自主学习知识梳理快乐学习
1.两条直线的位置关系
在同一平面内,两条直线的位置关系有__________和__________两种,若两条直线只有一个公共点,我们称这两条直线为__________.在同一平面内不相交的两条直线叫做__________.
【答案】相交,平行,相交线,平行线
【解析】
2.对顶角
()定义:如图所示,直线与相交于点,与有__________,它们的两边互为__________,这样的两个角叫做对顶角.
()性质:对顶角__________.
【答案】()公共顶点,反向延长线;()相等
【解析】
3.补角、余角
()定义:如果两个角的和是__________,那么称这两个角互为补角;如果两个角的和是__________,那么称这两个角互为余角.
()性质:同角或等角的补角__________,同角或等角的余角__________.
【答案】();()
【解析】
当堂达标
活学巧练
巩固基础
考点一:相交线与平行线
1.在同一平面内,两条直线的位置关系有(
).
A.重合、相交、平行三种
B.相交、重合两种
C.相交、平行两种
D.重合、平行两种
【答案】C
【解析】
2.同一平面内不重合的三条直线,其交点个数有(
)个.(数学思想链接:分类讨论思想)
【答案】或或或
【解析】
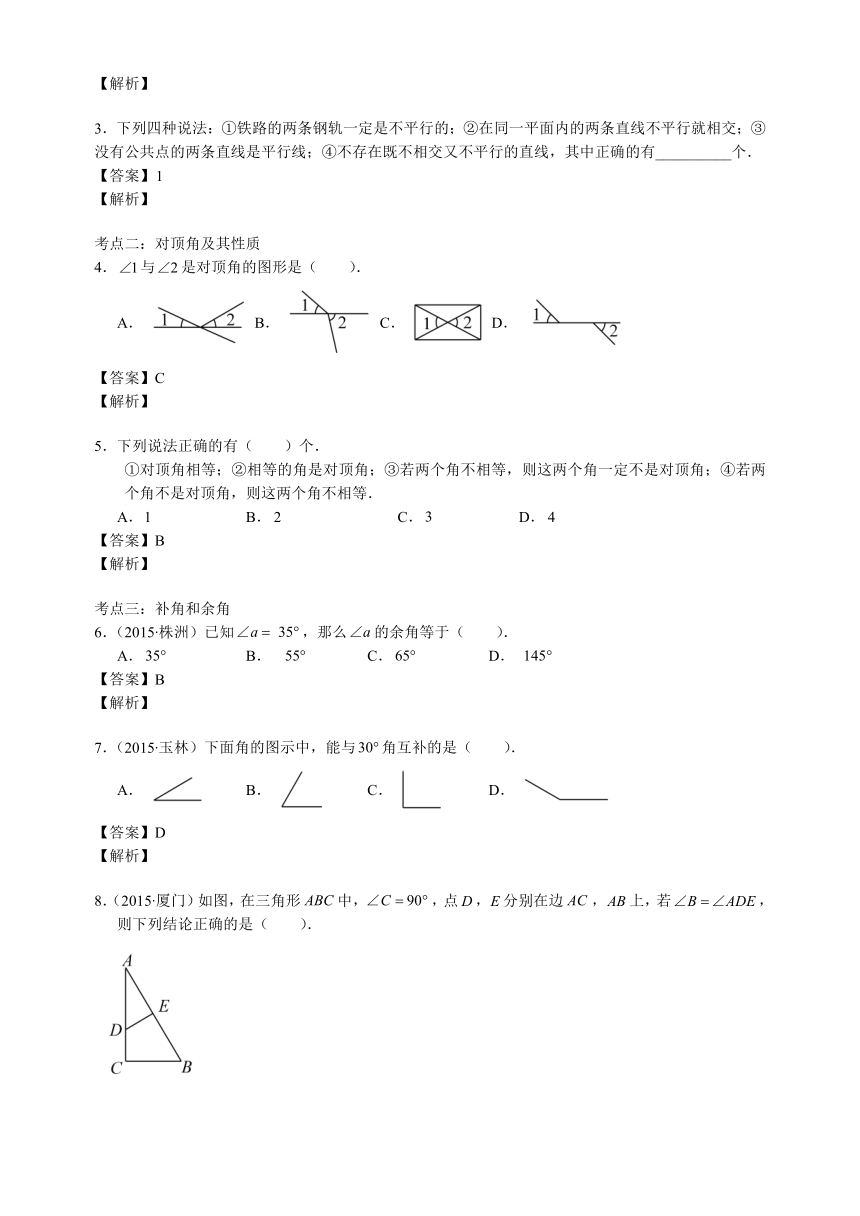
3.下列四种说法:①铁路的两条钢轨一定是不平行的;②在同一平面内的两条直线不平行就相交;③没有公共点的两条直线是平行线;④不存在既不相交又不平行的直线,其中正确的有__________个.
【答案】
【解析】
考点二:对顶角及其性质
4.与是对顶角的图形是(
).
A.B.C.D.
【答案】C
【解析】
5.下列说法正确的有(
)个.
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A.
B.
C.
D.
【答案】B
【解析】
考点三:补角和余角
6.(2015 株洲)已知,那么的余角等于(
).
A.
B.
C.
D.
【答案】B
【解析】
7.(2015 玉林)下面角的图示中,能与角互补的是(
).
A.
B.
C.
D.
【答案】D
【解析】
8.(2015 厦门)如图,在三角形中,,点,分别在边,上,若,则下列结论正确的是(
).
A.和互为补角
B.和互为补角
C.和互为余角
D.和互为余角
【答案】C
【解析】
9.如图,直线与相交于点,,则图中与的关系是(
).
A.互补
B.互余
C.相等
D.无法确定
【答案】C
【解析】
10.若,,则__________,理由是__________.
【答案】=,同角的余角相等
【解析】
11.已知与互补,与互余,试说明:.
【答案】见解析
【解析】解:因为与互补,与互余,
所以.
强化训练
综合演练
强化能力
1.(分)(2016 潍坊市潍城区期中)如果点在直线已上,也在直线上,但不在直线上,且直线,,两两相交,符合以上条件的图形是(
).
A.
B.C.D.
【答案】D
【解析】
2.(分)(2016 黔东南州期末)如图是对顶角量角器,则图中等于(
).
A.
B.
C.
D.
【答案】C
【解析】
3.(分)(2016 市北区期中)如图,,,在一条直线上,,,则图中互余的角共有(
).
A.对
B.对
C.对
D.对
【答案】B
【解析】
4.(分)如果和互补,且,则下列表示的余角的式子:①;②;③;④;其中正确的有(
).(数学思想链接:转化思想)
A.个
B.个
C.个
D.个
【答案】B
【解析】
5.(分)(2015 绥化)将一副三角尺按如图方式进行摆放,,不一定互补的是(
).
A.B.C.D.
【答案】D
【解析】
6.(分)(2016 青岛39中期末)一个角的补角的倍与它的余角的和为,则这个角的度数为___________度.
【答案】
【解析】
7.(分)如图所示,三条直线,,相交于同一点,则___________.(数学思想链接:转化思想)
【答案】
【解析】
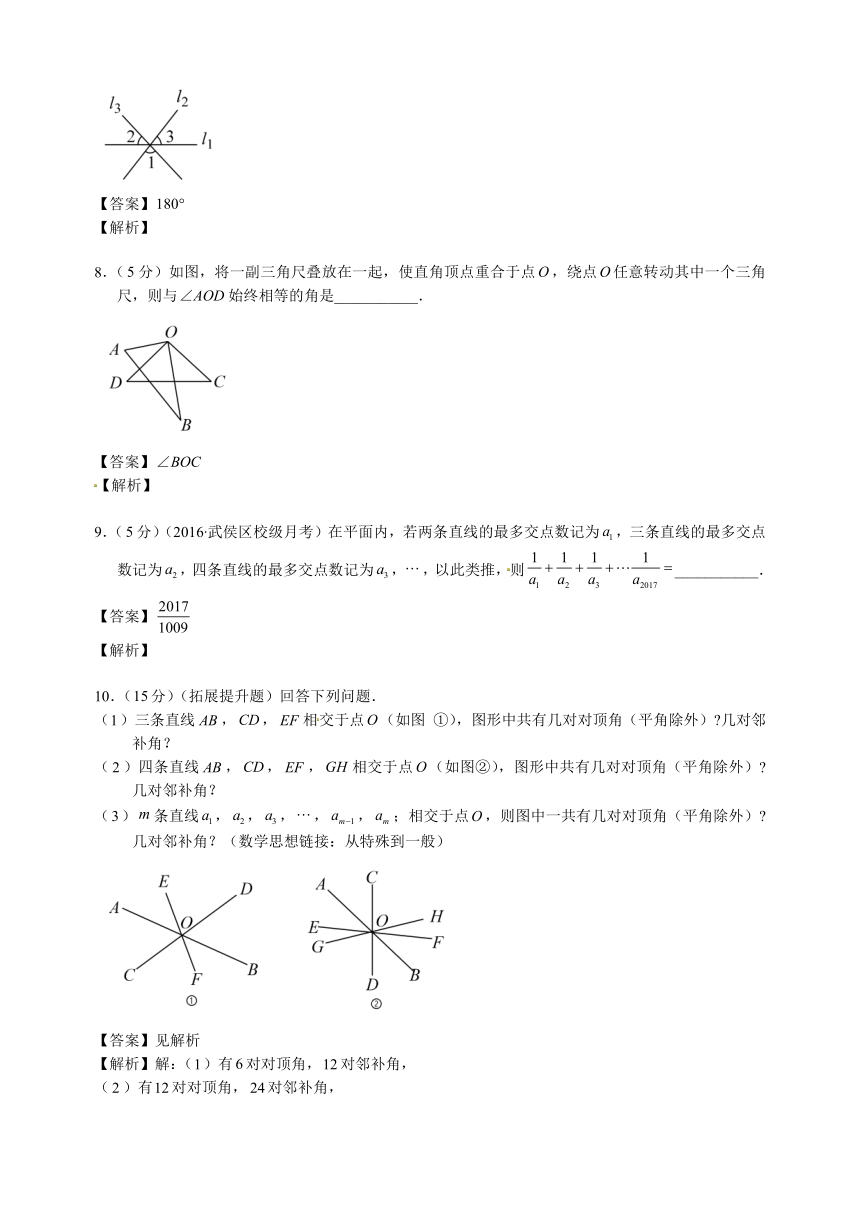
8.(分)如图,将一副三角尺叠放在一起,使直角顶点重合于点,绕点任意转动其中一个三角尺,则与始终相等的角是___________.
【答案】
【解析】
9.(分)(2016 武侯区校级月考)在平面内,若两条直线的最多交点数记为,三条直线的最多交点数记为,四条直线的最多交点数记为,,以此类推,则___________.
【答案】
【解析】
10.(分)(拓展提升题)回答下列问题.
()三条直线,,相交于点(如图
①),图形中共有几对对顶角(平角除外) 几对邻补角?
()四条直线,,,相交于点(如图②),图形中共有几对对顶角(平角除外) 几对邻补角?
()条直线,,,,,;相交于点,则图中一共有几对对顶角(平角除外) 几对邻补角?(数学思想链接:从特殊到一般)
【答案】见解析
【解析】解:()有对对顶角,对邻补角,
()有对对顶角,对邻补角,
()有对对顶角,对邻补角.
第2课时
垂线
自主学习
知识梳理
快乐学习
1.垂线的概念
两条直线相交成四个角,如果有一个角是__________,那么称这两条直线互相垂直,其中的一条直线叫做另一条直线的__________,它们的交点叫做垂足.通常用符号“”表示两条直线互相垂直.
【答案】直角,垂线
【解析】
2.垂线的性质
()平面内,过一点有且只有__________直线与已知直线垂直.
()直线外一点与直线上各点连接的所有线段中,__________最短.
【答案】()一条;()垂线段
【解析】
当堂达标
活学巧练
巩固基础
考点一:垂线的定义及画法
1.下列说法正确的是(
).
A.在同一平面内,过直线外一点向该直线画垂线,垂足一定在该直线上
B.在同一平面内,过线段或射线外一点向该线段或射线画垂线,垂足一定在该线段或射线上
C.过线段或射线外一点不一定能画出该线段或射线的垂线
D.过直线外一点与直线上一点画的一条直线与该直线垂直
【答案】A
【解析】
2.如图所示,.若,则的度数是(
).
A.
B.
C.
D.
【答案】C
【解析】
3.(2015·即墨28中期末)如图,,,,则__________.
【答案】
【解析】
4.如图,直线,相交于点,,分别是,上的点.用三角尺或量角器画图.
()经过点画直线的垂线.
()经过点画直线,的垂线.
()经过点分别画直线和的垂线.
【答案】略
【解析】
考点二:垂线的性质
5.在同一平面内,下列语句正确的是(
).
A.过一点有无数条直线与已知直线垂直
B.和一条直线垂直的直线有两条
C.过一点有且只有一条直线与已知直线垂直
D.两直线相交,则一定垂直
【答案】C
【解析】
6.如图,在一张透明的纸上画一条直线,在外任取一点并折出过点且与垂直的直线.这样的直线能折出(
).
A.条
B.条
C.条
D.条
【答案】B
【解析】
考点三:点到直线的距离
7.点到直线的距离是指(
).
A.直线外一点到这条直线的垂线的长度
B.直线外一点到这条直线上的任意一点的距离
C.直线外一点到这条直线的垂线段
D.直线外一点到这条直线的垂线段的长度
【答案】D
【解析】
8.如图是一名跳远运动员跳落沙坑时的痕迹,则表示该运动员成绩的是(
).
A.线段的长
B.线段的长
C.线段的长
D.线段的长
【答案】B
【解析】
9.如图所示,已知,,垂足分别是,,那么以下线段大小的比较必定成立的是(
).
A.
B.
C.
D.
【答案】C
【解析】
10.如图,,,,,则的长度(
).
A.大于
B.小于
C.大于或小于
D.大于且小于
【答案】D
【解析】
11.(2016 超银中学期中)如图,要在渠岸上找一点,在点处开沟,把水渠中的水引到点,要使沟最短,线段与渠岸的位置关系应是__________,理由是__________.
【答案】互相垂直,垂线段最短
【解析】
强化训练
综合演练
强化能力
1.(分)(2015 厦门)已知直线,,在同一平面内,若,垂足为点,,垂足也为点,则符合题意的图形可以是(
).
A.B.C.D.
【答案】C
【解析】
2.(分)(2016 淄博)如图,,,垂足分别为,,则图中能表示点到直线距离的线段共有(
).
A.条
B.条
C.条
D.条
【答案】D
【解析】
3.(分)如图,于点,于点,下列说法正确的是(
).
A.的余角只有
B.的补角是
C.是的余角
D.与互补
【答案】D
【解析】
4.(分)(2016 河北模拟)如图,直线与直线相交于点,,垂足为,已知,则的度数为(
).
A.
B.
C.
D.
【答案】C
【解析】
5.(分)(2016 常州)已知在三角形中,,,,垂足为,则的长可能是(
).
A.
B.
C.
D.
【答案】A
【解析】
6.(分)在直线上任取一点,过点作射线,,使,当时,
的度数是(
).(数学思想链接:分类讨论思想)
A.
B.
C.或
D.或
【答案】D
【解析】
7.(分)如图所示,已知直线,相交于点,于点,且比大,则
__________.(数学思想链接:方程思想)
【答案】
【解析】
8.(分)如图所示,河流在两个村庄,的附近,可以近似地看成是两条折线段(图中),,分别在河的两旁.现要在河边修建一个水泵站,同时向,两村供水,为了节约建设的费用,就要使所铺设的管道最短,甲提出了这样的建议:从向河道作垂线交于点,则点为水泵站的位置.
()你是否同意甲的意见?__________(填“是”或“否”).
()若同意,请说明理由;若不同意,那么你认为水泵站应该建在哪?请在图中作出来,并说明作图的依据.
【答案】见解析
【解析】解:()否;
()如图,连接,交于点,则水泵站应该建在处,依据为两点之间,线段最短.
9.(分)(拓展提升题)如图,点为直线上一点,为一射线,平分,平分.
()若,试探究,的位置关系,并说明理由.
()若为任意角,()中,的位置关系是否仍成立?请说明理由,由此你发现了什么规律?(数学思想链接:从特殊到一般)
【答案】见解析
【解析】解:().理由,
所以.
因为平分,平分,
所以,,
所以,
所以.
()成立.理由:因为,
所以.
因为平分,平分,
所以,,
所以,
所以.规律:邻补角的两条角平分线互相垂直.
相交线与平行线
1
两条直线的位置关系
第1课时
相交线与平行线
自主学习知识梳理快乐学习
1.两条直线的位置关系
在同一平面内,两条直线的位置关系有__________和__________两种,若两条直线只有一个公共点,我们称这两条直线为__________.在同一平面内不相交的两条直线叫做__________.
【答案】相交,平行,相交线,平行线
【解析】
2.对顶角
()定义:如图所示,直线与相交于点,与有__________,它们的两边互为__________,这样的两个角叫做对顶角.
()性质:对顶角__________.
【答案】()公共顶点,反向延长线;()相等
【解析】
3.补角、余角
()定义:如果两个角的和是__________,那么称这两个角互为补角;如果两个角的和是__________,那么称这两个角互为余角.
()性质:同角或等角的补角__________,同角或等角的余角__________.
【答案】();()
【解析】
当堂达标
活学巧练
巩固基础
考点一:相交线与平行线
1.在同一平面内,两条直线的位置关系有(
).
A.重合、相交、平行三种
B.相交、重合两种
C.相交、平行两种
D.重合、平行两种
【答案】C
【解析】
2.同一平面内不重合的三条直线,其交点个数有(
)个.(数学思想链接:分类讨论思想)
【答案】或或或
【解析】
3.下列四种说法:①铁路的两条钢轨一定是不平行的;②在同一平面内的两条直线不平行就相交;③没有公共点的两条直线是平行线;④不存在既不相交又不平行的直线,其中正确的有__________个.
【答案】
【解析】
考点二:对顶角及其性质
4.与是对顶角的图形是(
).
A.B.C.D.
【答案】C
【解析】
5.下列说法正确的有(
)个.
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A.
B.
C.
D.
【答案】B
【解析】
考点三:补角和余角
6.(2015 株洲)已知,那么的余角等于(
).
A.
B.
C.
D.
【答案】B
【解析】
7.(2015 玉林)下面角的图示中,能与角互补的是(
).
A.
B.
C.
D.
【答案】D
【解析】
8.(2015 厦门)如图,在三角形中,,点,分别在边,上,若,则下列结论正确的是(
).
A.和互为补角
B.和互为补角
C.和互为余角
D.和互为余角
【答案】C
【解析】
9.如图,直线与相交于点,,则图中与的关系是(
).
A.互补
B.互余
C.相等
D.无法确定
【答案】C
【解析】
10.若,,则__________,理由是__________.
【答案】=,同角的余角相等
【解析】
11.已知与互补,与互余,试说明:.
【答案】见解析
【解析】解:因为与互补,与互余,
所以.
强化训练
综合演练
强化能力
1.(分)(2016 潍坊市潍城区期中)如果点在直线已上,也在直线上,但不在直线上,且直线,,两两相交,符合以上条件的图形是(
).
A.
B.C.D.
【答案】D
【解析】
2.(分)(2016 黔东南州期末)如图是对顶角量角器,则图中等于(
).
A.
B.
C.
D.
【答案】C
【解析】
3.(分)(2016 市北区期中)如图,,,在一条直线上,,,则图中互余的角共有(
).
A.对
B.对
C.对
D.对
【答案】B
【解析】
4.(分)如果和互补,且,则下列表示的余角的式子:①;②;③;④;其中正确的有(
).(数学思想链接:转化思想)
A.个
B.个
C.个
D.个
【答案】B
【解析】
5.(分)(2015 绥化)将一副三角尺按如图方式进行摆放,,不一定互补的是(
).
A.B.C.D.
【答案】D
【解析】
6.(分)(2016 青岛39中期末)一个角的补角的倍与它的余角的和为,则这个角的度数为___________度.
【答案】
【解析】
7.(分)如图所示,三条直线,,相交于同一点,则___________.(数学思想链接:转化思想)
【答案】
【解析】
8.(分)如图,将一副三角尺叠放在一起,使直角顶点重合于点,绕点任意转动其中一个三角尺,则与始终相等的角是___________.
【答案】
【解析】
9.(分)(2016 武侯区校级月考)在平面内,若两条直线的最多交点数记为,三条直线的最多交点数记为,四条直线的最多交点数记为,,以此类推,则___________.
【答案】
【解析】
10.(分)(拓展提升题)回答下列问题.
()三条直线,,相交于点(如图
①),图形中共有几对对顶角(平角除外) 几对邻补角?
()四条直线,,,相交于点(如图②),图形中共有几对对顶角(平角除外) 几对邻补角?
()条直线,,,,,;相交于点,则图中一共有几对对顶角(平角除外) 几对邻补角?(数学思想链接:从特殊到一般)
【答案】见解析
【解析】解:()有对对顶角,对邻补角,
()有对对顶角,对邻补角,
()有对对顶角,对邻补角.
第2课时
垂线
自主学习
知识梳理
快乐学习
1.垂线的概念
两条直线相交成四个角,如果有一个角是__________,那么称这两条直线互相垂直,其中的一条直线叫做另一条直线的__________,它们的交点叫做垂足.通常用符号“”表示两条直线互相垂直.
【答案】直角,垂线
【解析】
2.垂线的性质
()平面内,过一点有且只有__________直线与已知直线垂直.
()直线外一点与直线上各点连接的所有线段中,__________最短.
【答案】()一条;()垂线段
【解析】
当堂达标
活学巧练
巩固基础
考点一:垂线的定义及画法
1.下列说法正确的是(
).
A.在同一平面内,过直线外一点向该直线画垂线,垂足一定在该直线上
B.在同一平面内,过线段或射线外一点向该线段或射线画垂线,垂足一定在该线段或射线上
C.过线段或射线外一点不一定能画出该线段或射线的垂线
D.过直线外一点与直线上一点画的一条直线与该直线垂直
【答案】A
【解析】
2.如图所示,.若,则的度数是(
).
A.
B.
C.
D.
【答案】C
【解析】
3.(2015·即墨28中期末)如图,,,,则__________.
【答案】
【解析】
4.如图,直线,相交于点,,分别是,上的点.用三角尺或量角器画图.
()经过点画直线的垂线.
()经过点画直线,的垂线.
()经过点分别画直线和的垂线.
【答案】略
【解析】
考点二:垂线的性质
5.在同一平面内,下列语句正确的是(
).
A.过一点有无数条直线与已知直线垂直
B.和一条直线垂直的直线有两条
C.过一点有且只有一条直线与已知直线垂直
D.两直线相交,则一定垂直
【答案】C
【解析】
6.如图,在一张透明的纸上画一条直线,在外任取一点并折出过点且与垂直的直线.这样的直线能折出(
).
A.条
B.条
C.条
D.条
【答案】B
【解析】
考点三:点到直线的距离
7.点到直线的距离是指(
).
A.直线外一点到这条直线的垂线的长度
B.直线外一点到这条直线上的任意一点的距离
C.直线外一点到这条直线的垂线段
D.直线外一点到这条直线的垂线段的长度
【答案】D
【解析】
8.如图是一名跳远运动员跳落沙坑时的痕迹,则表示该运动员成绩的是(
).
A.线段的长
B.线段的长
C.线段的长
D.线段的长
【答案】B
【解析】
9.如图所示,已知,,垂足分别是,,那么以下线段大小的比较必定成立的是(
).
A.
B.
C.
D.
【答案】C
【解析】
10.如图,,,,,则的长度(
).
A.大于
B.小于
C.大于或小于
D.大于且小于
【答案】D
【解析】
11.(2016 超银中学期中)如图,要在渠岸上找一点,在点处开沟,把水渠中的水引到点,要使沟最短,线段与渠岸的位置关系应是__________,理由是__________.
【答案】互相垂直,垂线段最短
【解析】
强化训练
综合演练
强化能力
1.(分)(2015 厦门)已知直线,,在同一平面内,若,垂足为点,,垂足也为点,则符合题意的图形可以是(
).
A.B.C.D.
【答案】C
【解析】
2.(分)(2016 淄博)如图,,,垂足分别为,,则图中能表示点到直线距离的线段共有(
).
A.条
B.条
C.条
D.条
【答案】D
【解析】
3.(分)如图,于点,于点,下列说法正确的是(
).
A.的余角只有
B.的补角是
C.是的余角
D.与互补
【答案】D
【解析】
4.(分)(2016 河北模拟)如图,直线与直线相交于点,,垂足为,已知,则的度数为(
).
A.
B.
C.
D.
【答案】C
【解析】
5.(分)(2016 常州)已知在三角形中,,,,垂足为,则的长可能是(
).
A.
B.
C.
D.
【答案】A
【解析】
6.(分)在直线上任取一点,过点作射线,,使,当时,
的度数是(
).(数学思想链接:分类讨论思想)
A.
B.
C.或
D.或
【答案】D
【解析】
7.(分)如图所示,已知直线,相交于点,于点,且比大,则
__________.(数学思想链接:方程思想)
【答案】
【解析】
8.(分)如图所示,河流在两个村庄,的附近,可以近似地看成是两条折线段(图中),,分别在河的两旁.现要在河边修建一个水泵站,同时向,两村供水,为了节约建设的费用,就要使所铺设的管道最短,甲提出了这样的建议:从向河道作垂线交于点,则点为水泵站的位置.
()你是否同意甲的意见?__________(填“是”或“否”).
()若同意,请说明理由;若不同意,那么你认为水泵站应该建在哪?请在图中作出来,并说明作图的依据.
【答案】见解析
【解析】解:()否;
()如图,连接,交于点,则水泵站应该建在处,依据为两点之间,线段最短.
9.(分)(拓展提升题)如图,点为直线上一点,为一射线,平分,平分.
()若,试探究,的位置关系,并说明理由.
()若为任意角,()中,的位置关系是否仍成立?请说明理由,由此你发现了什么规律?(数学思想链接:从特殊到一般)
【答案】见解析
【解析】解:().理由,
所以.
因为平分,平分,
所以,,
所以,
所以.
()成立.理由:因为,
所以.
因为平分,平分,
所以,,
所以,
所以.规律:邻补角的两条角平分线互相垂直.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
