北师大版七年级数学下册第四章三角形3探索三角形全等的条件 学案(含答案)
文档属性
| 名称 | 北师大版七年级数学下册第四章三角形3探索三角形全等的条件 学案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 634.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-08-26 20:27:38 | ||
图片预览




文档简介
3
探索三角形全等的条件
第1课时
三角形全等的条件——边边边
自主学习
知识梳理
快乐学习
1.三角形全等的条件()
()三边分别__________的两个三角形全等,简写为“边边边”或“__________”.
()如图,已知,要使≌,则只需添加一个适当的条件是__________.(填一个即可)
【答案】()相等;
()
【解析】
2.三角形的稳定性
只要三角形三边的长度确定了,它的__________和__________就完全确定了,三角形的这个性质
叫做三角形的稳定性.
【答案】形状;大小
【解析】
当堂达标
活学巧练
巩固基础
考点一:“边边边”
1.如图所示,中,,,,则根据“”能直接判定(
).
A.≌
B.≌
C.≌
D.≌
【答案】C
【解析】
2.(一题多辨)()如图①,已知,,点,,,在一条直线上,要利用“”说明≌,还可以添加的一个条件是(
).
A.
B.
C.
D.以上都不对
()如图②,在和中,,,要利用“”来判定和全等时,下面的个条件中:①;②;③;④,可利用的是(
).
A.①或②
B.②或③
C.①或③
D.①或④
【答案】()A
()A
【解析】
3.如图,在与中,已知,在不添加任何辅助线的前提下,要使≌,只需再添加的一个条件是__________.
【答案】
【解析】
考点二:“边边边”的应用
4.如图,,,,则等于(
).
A.
B.
C.
D.
【答案】D
【解析】
5.如图,已知,,,则下列结论中:①≌;②;③;④;⑤.正确的个数是(
).
A.
B.
C.
D.
【答案】D
【解析】
6.如图,是的中点,,.试说明:.
【答案】见解析
【解析】解:因为是的中点,
所以.
在和中,
因为,,,
所以≌,
所以(全等三角形对应角相等).
考点三:三角形的稳定性
7.如图所示,建高楼常需要用塔吊来吊建筑材料,而塔吊的上部是三角形结构,这是应用了三角形的
哪个性质?答:__________.(填“稳定性”或“不稳定性”)
【答案】稳定性
【解析】
强化训练
综合演练
强化能力
1.(分)如图所示,小龙的爸爸买了一张桌子,桌面下有两个三角形,即图中的和,设计两个三角形的主要原因是(
).
A.使≌
B.利用三角形的稳定性使桌子稳固
C.使两个三角形是全等的直角三角形
D.对称美
【答案】B
【解析】
2.(分)如图,,,,,则的度数是(
)(数学思想链接:转化思想)
A.
B.
C.
D.
【答案】C
【解析】
3.(分)如图,是不等边三角形,,以,为两个顶点作位置不同的三角形,使所作三角形与全等,这样的三角形最多可以作出(
).
A.个
B.个
C.个
D.个
【答案】B
【解析】
4.(分)如图,生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有__________性.
【答案】稳定
【解析】
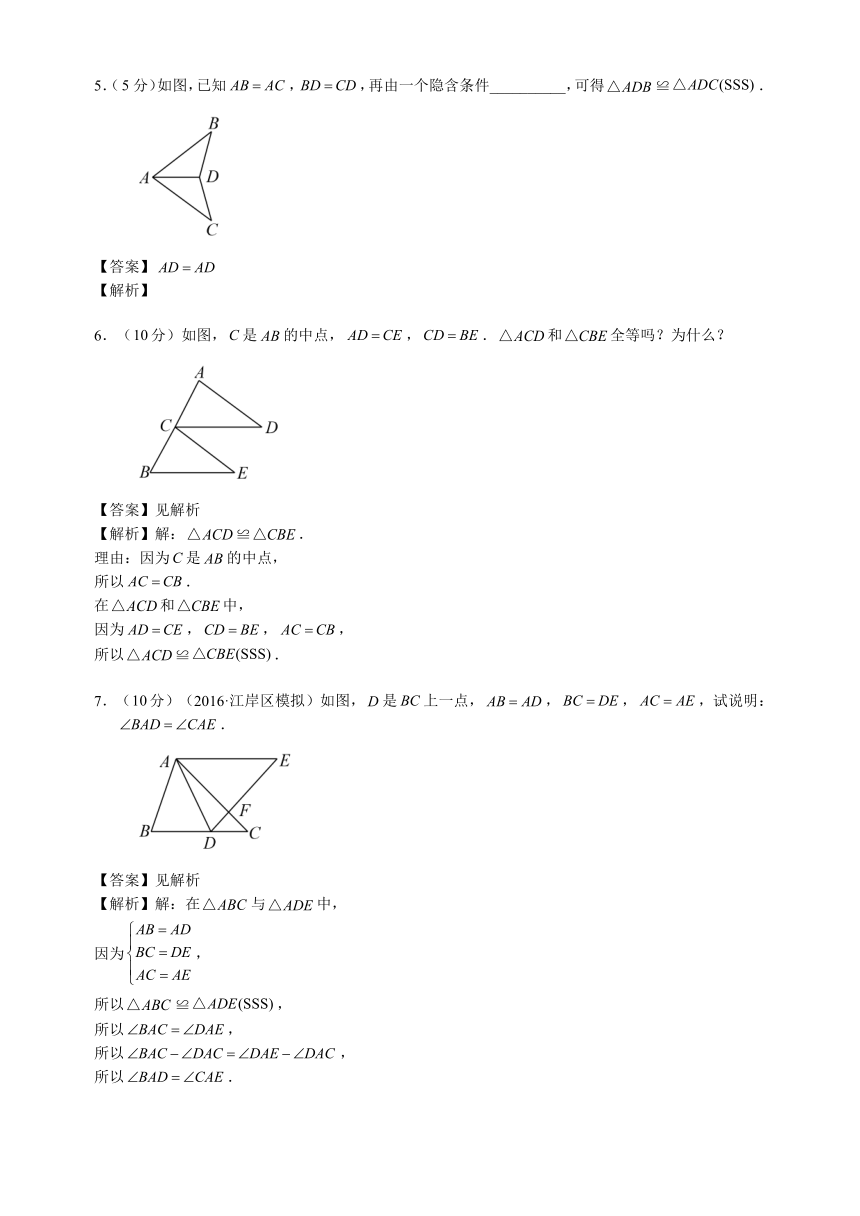
5.(分)如图,已知,,再由一个隐含条件__________,可得≌.
【答案】
【解析】
6.(分)如图,是的中点,,.和全等吗?为什么?
【答案】见解析
【解析】解:≌.
理由:因为是的中点,
所以.
在和中,
因为,,,
所以≌.
7.(分)(2016·江岸区模拟)如图,是上一点,,,,试说明:.
【答案】见解析
【解析】解:在与中,
因为,
所以≌,
所以,
所以,
所以.
8.(拓展提升题)(分)(2016·河北)如图,点,,,在直线上(,之间不能直接测量),点,在异侧,测得,,.
()试说明:≌.
()指出图中所有平行的线段,并说明理由.
【答案】见解析
【解析】解:()因为,
所以,即.
在和中,
因为,
所以≌.
(),.
理由:因为≌,
所以,,
所以,.
第2课时
三角形全等的条件——角边角或角角边
自主学习
知识梳理
快乐学习
1.三角形全等的条件(2)
两角及其夹边分别相等的两个三角形全等,简写成“__________”或“__________”.
【答案】角边角;
【解析】
2.三角形全等的条件(3)
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写成“__________”或“__________”.
【答案】角角边;
【解析】
当堂达标
活学巧练
巩固基础
考点一:“角边角”
1.如图,已知的六个元素,则下列甲、乙、丙三个三角形中一定和全等的是(
).
A.甲、乙
B.甲、丙
C.乙、丙
D.乙
【答案】C
【解析】
2.如图,线段,相交于点,若,为了用“”判定≌,则应补充条件(
).
A.
B.
C.
D.
【答案】A
【解析】
3.如图,在四边形中,,若用“”说明≌,需添加条件__________.
【答案】
【解析】
考点二:“角角边”
4.如图,己知,,那么添加下列一个条件后,仍无法判定≌的是(
).
A.
B.
C.
D.
【答案】B
【解析】
5.(一题多辨)()如图①,在上,在上,且,则下列条件中,无法判定
≌的是(
).
A.
B.
C.
D.
()如图②,已知,添加一个条件使≌(不标注新的字母,不添加新的线段),你添加的条件是__________.
【答案】()D
()示例:
【解析】
6.如图,在中,,点是边上的一点,,且,过点作
交于点,则≌__________,理由是__________.
【答案】;(答案不唯一)
【解析】
考点三:“角边角”及“角角边”的应用
7.如图,,,是和的公共边,所以就可以判定
≌.你认为这种说法正确吗?如果不正确,请说明理由.
【答案】见解析
【解析】解:不正确.因为虽然是和的公共边,但它们不是对应边.
强化训练
综合演练
强化能力
1.(分)如图所示,,是的中点,直接应用“”说明≌,还需要的条件是(
).
A.
B.
C.
D.
【答案】B
【解析】
2.(分)如图,已知,,那么要得到≌,还应给出的条件是(
).
A.
B.
C.
D.
【答案】D
【解析】
3.(分)如图,,,,,则等于(
).
A.
B.
C.
D.
【答案】B
【解析】
4.(分)小明不慎将一块三角形玻璃打碎成如图所示的四块,现要到玻璃店配一个与原来一样大小的三角形玻璃,你认为应带去的一块是(
).
A.第①块
B.第②块
C.第③块
D.第④块
【答案】B
【解析】
5.(分)如图,已知为直线上一点,,,请写出图中一组相等的线段__________.
【答案】示例:
【解析】
6.(分)如图所示,,,垂足分别为,,且,相交于点,.
图中全等的三角形共有__________对.
【答案】
【解析】
7.(分)(2016 济宁)如图,中,,,垂足分别为,,,交于点,请你添加一个适当的条件:__________,使≌.
【答案】示例:
【解析】
8.(分)(2015 黄岛区期末)如图,,,,,,,则__________.
【答案】
【解析】
9.(分)(拓展提升题)(2015 胶南市王台中学质检)是经过顶点的一条直线,.,分别是直线上两点,且.
()若直线经过的内部,且,在射线上,请解决下面两个问题:
①如图①,若,,则__________;__________(填“>”“<”或“=”);
②如图②,若,请添加一个关于与关系的条件__________,使①中的两个结论仍然成立,并证明两个结论成立.
()如图③,若直线经过的外部,,请提出,,三条线段数量关系的合理猜想(不要求证明).
【答案】见解析
【解析】解:()①,;②所填的条件是:.
证明:在中,.
因为,
所以,
又因为,
所以.
又因为,,
所以≌,
所以,.
又因为,
所以.
()猜想:.
第3课时
三角形全等的条件——边角边
自主学习
知识梳理
快乐学习
三角形全等的条件(4)
()两边及其__________分别相等的两个三角形全等,简写成“边角边”或__________.
()判定条件“”用符号可表示为:如图所示,在和中,如果,__________,__________,则≌.
()我们已经学习了四种说明两个三角形全等的方法,即__________、__________、__________和__________,
【答案】()夹角,
(),
(),,,
【解析】
当堂达标
活学巧练
巩固基础
考点一:边角边
1.如图,,分别在,上,且,,则≌的依据是(
).
A.
B.
C.
D.
【答案】C
【解析】
2.下列条件,不能判定两个三角形全等的是(
).
A.两边及一角对应相等
B.两角及其中一角的对边对应相等
C.三边对应相等
D.两边及其夹角对应相等
【答案】A
【解析】
3.(一题多辨)()如图①,在四边形中,,,若连接,相交于点,则图中全等三角形共有(
).
A.对
B.对
C.对
D.对
()(2016 成安县期末)如图②,于点,,图中共有全等三角形__________对.
【答案】()C
()
【解析】
4.如图,已知,,若要得到≌,必须添加一个条件,则下列所添条件不成立的是(
).
A.
B.
C.
D.
【答案】B
【解析】
考点二:“”的应用
5.如图,将两根弯曲的钢条,的中点连在一起,使,可以绕着点自由转动,就做成了一个测量工件,则的长等于内槽宽,那么判定≌的依据是(
).
A.边角边
B.角边角
C.边边边
D.角角边
【答案】A
【解析】
6.(2015·胶南市王台中学质检)已知和都是等腰直角三角形,如图摆放使得一直角边重合,连接,.问:和有何位置关系?并说明理由.
【答案】见解析
【解析】解:.理由如下:因为和都是等腰直角三角形,
所以,,.
在和中,
因为,
所以≌,
所以.
又因为,
所以,
所以,即.
强化训练
综合演练
强化能力
1.(分)(2016·新疆)如图,在和中,,,添加下列一个条件后,仍然不能说明≌,这个条件是(
).
A.
B.
C.
D.
【答案】D
【解析】
2.(分)(2015·黄岛区期末)如图,,,以下条件中,不能推出≌
的是(
).
A.
B.
C.
D.
【答案】C
【解析】
3.(分)(2016·河北模拟)如图,在正方形中,,延长到点,使,连接,动点从点出发以每秒个单位长度的速度沿向终点运动,设点的运动时间为秒,当和全等时,的值为(
)(数学思想链接:分类讨论思想)
A.
B.
C.
D.或
【答案】D
【解析】
4.(分)(2015·胶州市期末)如图,已知平分,要使≌,只需再添加一个条件就可以了,你选择的条件是__________,理由是__________.
【答案】示例:,
【解析】
5.(分)如图,已知米,于点,米,射线于点,点从点
向点运动,每秒走米,点从点问点运动,每秒走米,,同时从点出发,则出发__________秒后,在线段上有一点,使与全等.(方法链接:动点问题)
【答案】
【解析】
6.(分)如图,和相交于点,,,和平行吗?为什么?
【答案】见解析
【解析】解:.理由:在和中,
因为,,,
所以≌,
所以,
所以.
7.(分)(2015 黄岛区期末)如图,在等腰中,,延长至点,使,连接,以为边作等腰,使,,连接交于点.
()吗?请说明理由.
()若,求的度数.
【答案】见解析
【解析】解:().理由如下:因为,
所以,
所以.
在和中,
因为,
所以≌,
所以.
()因为,,
所以,由()得:≌,
所以.
因为,,
所以.
8.(分)(拓展提升题)如图①,,,点是上一点,且,.
()试判断与的位置关系,并说明理由.
()如图②,若把沿直线向左平移,使的顶点与重合,此时问题()中的位置关系还成立吗?请说明理由.(注意字母的变化)
【答案】见解析
【解析】解:().理由如下:因为,,
所以.又,,
所以≌.
所以.
因为,
所以,
所以.
所以.
()问题()中的位置关系还成立.理由:因为,,
所以.
又,,
所以≌.
所以.
又,
所以.
所以.
所以.
探索三角形全等的条件
第1课时
三角形全等的条件——边边边
自主学习
知识梳理
快乐学习
1.三角形全等的条件()
()三边分别__________的两个三角形全等,简写为“边边边”或“__________”.
()如图,已知,要使≌,则只需添加一个适当的条件是__________.(填一个即可)
【答案】()相等;
()
【解析】
2.三角形的稳定性
只要三角形三边的长度确定了,它的__________和__________就完全确定了,三角形的这个性质
叫做三角形的稳定性.
【答案】形状;大小
【解析】
当堂达标
活学巧练
巩固基础
考点一:“边边边”
1.如图所示,中,,,,则根据“”能直接判定(
).
A.≌
B.≌
C.≌
D.≌
【答案】C
【解析】
2.(一题多辨)()如图①,已知,,点,,,在一条直线上,要利用“”说明≌,还可以添加的一个条件是(
).
A.
B.
C.
D.以上都不对
()如图②,在和中,,,要利用“”来判定和全等时,下面的个条件中:①;②;③;④,可利用的是(
).
A.①或②
B.②或③
C.①或③
D.①或④
【答案】()A
()A
【解析】
3.如图,在与中,已知,在不添加任何辅助线的前提下,要使≌,只需再添加的一个条件是__________.
【答案】
【解析】
考点二:“边边边”的应用
4.如图,,,,则等于(
).
A.
B.
C.
D.
【答案】D
【解析】
5.如图,已知,,,则下列结论中:①≌;②;③;④;⑤.正确的个数是(
).
A.
B.
C.
D.
【答案】D
【解析】
6.如图,是的中点,,.试说明:.
【答案】见解析
【解析】解:因为是的中点,
所以.
在和中,
因为,,,
所以≌,
所以(全等三角形对应角相等).
考点三:三角形的稳定性
7.如图所示,建高楼常需要用塔吊来吊建筑材料,而塔吊的上部是三角形结构,这是应用了三角形的
哪个性质?答:__________.(填“稳定性”或“不稳定性”)
【答案】稳定性
【解析】
强化训练
综合演练
强化能力
1.(分)如图所示,小龙的爸爸买了一张桌子,桌面下有两个三角形,即图中的和,设计两个三角形的主要原因是(
).
A.使≌
B.利用三角形的稳定性使桌子稳固
C.使两个三角形是全等的直角三角形
D.对称美
【答案】B
【解析】
2.(分)如图,,,,,则的度数是(
)(数学思想链接:转化思想)
A.
B.
C.
D.
【答案】C
【解析】
3.(分)如图,是不等边三角形,,以,为两个顶点作位置不同的三角形,使所作三角形与全等,这样的三角形最多可以作出(
).
A.个
B.个
C.个
D.个
【答案】B
【解析】
4.(分)如图,生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有__________性.
【答案】稳定
【解析】
5.(分)如图,已知,,再由一个隐含条件__________,可得≌.
【答案】
【解析】
6.(分)如图,是的中点,,.和全等吗?为什么?
【答案】见解析
【解析】解:≌.
理由:因为是的中点,
所以.
在和中,
因为,,,
所以≌.
7.(分)(2016·江岸区模拟)如图,是上一点,,,,试说明:.
【答案】见解析
【解析】解:在与中,
因为,
所以≌,
所以,
所以,
所以.
8.(拓展提升题)(分)(2016·河北)如图,点,,,在直线上(,之间不能直接测量),点,在异侧,测得,,.
()试说明:≌.
()指出图中所有平行的线段,并说明理由.
【答案】见解析
【解析】解:()因为,
所以,即.
在和中,
因为,
所以≌.
(),.
理由:因为≌,
所以,,
所以,.
第2课时
三角形全等的条件——角边角或角角边
自主学习
知识梳理
快乐学习
1.三角形全等的条件(2)
两角及其夹边分别相等的两个三角形全等,简写成“__________”或“__________”.
【答案】角边角;
【解析】
2.三角形全等的条件(3)
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写成“__________”或“__________”.
【答案】角角边;
【解析】
当堂达标
活学巧练
巩固基础
考点一:“角边角”
1.如图,已知的六个元素,则下列甲、乙、丙三个三角形中一定和全等的是(
).
A.甲、乙
B.甲、丙
C.乙、丙
D.乙
【答案】C
【解析】
2.如图,线段,相交于点,若,为了用“”判定≌,则应补充条件(
).
A.
B.
C.
D.
【答案】A
【解析】
3.如图,在四边形中,,若用“”说明≌,需添加条件__________.
【答案】
【解析】
考点二:“角角边”
4.如图,己知,,那么添加下列一个条件后,仍无法判定≌的是(
).
A.
B.
C.
D.
【答案】B
【解析】
5.(一题多辨)()如图①,在上,在上,且,则下列条件中,无法判定
≌的是(
).
A.
B.
C.
D.
()如图②,已知,添加一个条件使≌(不标注新的字母,不添加新的线段),你添加的条件是__________.
【答案】()D
()示例:
【解析】
6.如图,在中,,点是边上的一点,,且,过点作
交于点,则≌__________,理由是__________.
【答案】;(答案不唯一)
【解析】
考点三:“角边角”及“角角边”的应用
7.如图,,,是和的公共边,所以就可以判定
≌.你认为这种说法正确吗?如果不正确,请说明理由.
【答案】见解析
【解析】解:不正确.因为虽然是和的公共边,但它们不是对应边.
强化训练
综合演练
强化能力
1.(分)如图所示,,是的中点,直接应用“”说明≌,还需要的条件是(
).
A.
B.
C.
D.
【答案】B
【解析】
2.(分)如图,已知,,那么要得到≌,还应给出的条件是(
).
A.
B.
C.
D.
【答案】D
【解析】
3.(分)如图,,,,,则等于(
).
A.
B.
C.
D.
【答案】B
【解析】
4.(分)小明不慎将一块三角形玻璃打碎成如图所示的四块,现要到玻璃店配一个与原来一样大小的三角形玻璃,你认为应带去的一块是(
).
A.第①块
B.第②块
C.第③块
D.第④块
【答案】B
【解析】
5.(分)如图,已知为直线上一点,,,请写出图中一组相等的线段__________.
【答案】示例:
【解析】
6.(分)如图所示,,,垂足分别为,,且,相交于点,.
图中全等的三角形共有__________对.
【答案】
【解析】
7.(分)(2016 济宁)如图,中,,,垂足分别为,,,交于点,请你添加一个适当的条件:__________,使≌.
【答案】示例:
【解析】
8.(分)(2015 黄岛区期末)如图,,,,,,,则__________.
【答案】
【解析】
9.(分)(拓展提升题)(2015 胶南市王台中学质检)是经过顶点的一条直线,.,分别是直线上两点,且.
()若直线经过的内部,且,在射线上,请解决下面两个问题:
①如图①,若,,则__________;__________(填“>”“<”或“=”);
②如图②,若,请添加一个关于与关系的条件__________,使①中的两个结论仍然成立,并证明两个结论成立.
()如图③,若直线经过的外部,,请提出,,三条线段数量关系的合理猜想(不要求证明).
【答案】见解析
【解析】解:()①,;②所填的条件是:.
证明:在中,.
因为,
所以,
又因为,
所以.
又因为,,
所以≌,
所以,.
又因为,
所以.
()猜想:.
第3课时
三角形全等的条件——边角边
自主学习
知识梳理
快乐学习
三角形全等的条件(4)
()两边及其__________分别相等的两个三角形全等,简写成“边角边”或__________.
()判定条件“”用符号可表示为:如图所示,在和中,如果,__________,__________,则≌.
()我们已经学习了四种说明两个三角形全等的方法,即__________、__________、__________和__________,
【答案】()夹角,
(),
(),,,
【解析】
当堂达标
活学巧练
巩固基础
考点一:边角边
1.如图,,分别在,上,且,,则≌的依据是(
).
A.
B.
C.
D.
【答案】C
【解析】
2.下列条件,不能判定两个三角形全等的是(
).
A.两边及一角对应相等
B.两角及其中一角的对边对应相等
C.三边对应相等
D.两边及其夹角对应相等
【答案】A
【解析】
3.(一题多辨)()如图①,在四边形中,,,若连接,相交于点,则图中全等三角形共有(
).
A.对
B.对
C.对
D.对
()(2016 成安县期末)如图②,于点,,图中共有全等三角形__________对.
【答案】()C
()
【解析】
4.如图,已知,,若要得到≌,必须添加一个条件,则下列所添条件不成立的是(
).
A.
B.
C.
D.
【答案】B
【解析】
考点二:“”的应用
5.如图,将两根弯曲的钢条,的中点连在一起,使,可以绕着点自由转动,就做成了一个测量工件,则的长等于内槽宽,那么判定≌的依据是(
).
A.边角边
B.角边角
C.边边边
D.角角边
【答案】A
【解析】
6.(2015·胶南市王台中学质检)已知和都是等腰直角三角形,如图摆放使得一直角边重合,连接,.问:和有何位置关系?并说明理由.
【答案】见解析
【解析】解:.理由如下:因为和都是等腰直角三角形,
所以,,.
在和中,
因为,
所以≌,
所以.
又因为,
所以,
所以,即.
强化训练
综合演练
强化能力
1.(分)(2016·新疆)如图,在和中,,,添加下列一个条件后,仍然不能说明≌,这个条件是(
).
A.
B.
C.
D.
【答案】D
【解析】
2.(分)(2015·黄岛区期末)如图,,,以下条件中,不能推出≌
的是(
).
A.
B.
C.
D.
【答案】C
【解析】
3.(分)(2016·河北模拟)如图,在正方形中,,延长到点,使,连接,动点从点出发以每秒个单位长度的速度沿向终点运动,设点的运动时间为秒,当和全等时,的值为(
)(数学思想链接:分类讨论思想)
A.
B.
C.
D.或
【答案】D
【解析】
4.(分)(2015·胶州市期末)如图,已知平分,要使≌,只需再添加一个条件就可以了,你选择的条件是__________,理由是__________.
【答案】示例:,
【解析】
5.(分)如图,已知米,于点,米,射线于点,点从点
向点运动,每秒走米,点从点问点运动,每秒走米,,同时从点出发,则出发__________秒后,在线段上有一点,使与全等.(方法链接:动点问题)
【答案】
【解析】
6.(分)如图,和相交于点,,,和平行吗?为什么?
【答案】见解析
【解析】解:.理由:在和中,
因为,,,
所以≌,
所以,
所以.
7.(分)(2015 黄岛区期末)如图,在等腰中,,延长至点,使,连接,以为边作等腰,使,,连接交于点.
()吗?请说明理由.
()若,求的度数.
【答案】见解析
【解析】解:().理由如下:因为,
所以,
所以.
在和中,
因为,
所以≌,
所以.
()因为,,
所以,由()得:≌,
所以.
因为,,
所以.
8.(分)(拓展提升题)如图①,,,点是上一点,且,.
()试判断与的位置关系,并说明理由.
()如图②,若把沿直线向左平移,使的顶点与重合,此时问题()中的位置关系还成立吗?请说明理由.(注意字母的变化)
【答案】见解析
【解析】解:().理由如下:因为,,
所以.又,,
所以≌.
所以.
因为,
所以,
所以.
所以.
()问题()中的位置关系还成立.理由:因为,,
所以.
又,,
所以≌.
所以.
又,
所以.
所以.
所以.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
