北师大版七年级数学下册第一章整式的乘除6完全平方公式 学案(含答案)
文档属性
| 名称 | 北师大版七年级数学下册第一章整式的乘除6完全平方公式 学案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 545.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-08-26 20:19:45 | ||
图片预览




文档简介
6
完全平方公式
第1课时
完全平方公式
自主学习
知识梳理快乐学习
完全平方公式
两个数的和的平方等于这两个数的平方和与它们积的倍的和;两个数的差的平方等于这两个数的平方和与它们积的倍的差.用字母表示为:__________,__________.
【答案】
【解析】
当堂达标
活学巧练巩固基础
考点一:完全平方式的特征
1.计算结果是完全平方式的为(
).
A.
B.
C.
D.
【答案】C
【解析】
2.多项式加上一个单项式后能成为一个完全平方式,则加上的单项式不可以是(
).
A.
B.
C.
D.
【答案】D
【解析】
3.若是完全平方式,则等于(
).
A.
B.
C.
D.
【答案】A
【解析】
4.(2016·市北区期中)是完全平方式,则__________.(数学思想链接:分类讨论思想)
【答案】
【解析】
考点二:完全平方公式
5.下列多项式中,不能用完全平方公式计算的是(
).
A.
B.
C.
D.
【答案】D
【解析】
6.下列计算正确的是(
).
A.
B.
C.
D.
【答案】C
【解析】
7.下列式子错误的是(
).
A.
B.
C.
D.
【答案】D
【解析】
8.(一题多辨)()若,则为(
).
A.
B.
C.
D.
()已知,,则(
).
A.
B.
C.
D.
()已知有理数满足,则__________.
【答案】()C
()A
()
【解析】
9.运算结果为的是(
).
A.
B.
C.
D.
【答案】B
【解析】
10.如图,最大的正方形的面积是(
).
A.
B.
C.
D.
【答案】C
【解析】
11.__________.
【答案】
【解析】
12.计算.
().
().
()(2016·市北区期中).
【答案】见解析
【解析】()原式.
()原式.
()原式
.
13.(2016·常州)先化简,再求值:,其中.
【答案】见解析
【解析】解:原式,
,
,
当时,
原式.
强化训练
综合演练强化能力
1.(分)(2016·武汉)运用乘法公式计算的结果是(
).
A.
B.
C.
D.
【答案】C
【解析】
2.(分)(2016·育才中学期中)若,那么等于(
).
A.
B.
C.
D.
【答案】D
【解析】
3.(分)(一题多辨)()已知,,则的值为(
)(数学思想链接:整体思想)
A.
B.
C.
D.
()(2015·胶南市王台中学质检)若,,则__________.
【答案】()C
()
【解析】
4.(分)图①是一个长为,宽为的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四个形状和大小都一样的小长方形,然后按图②那样拼成一个正方形,则中间空的部分的面积是(
).
A.
B.
C.
D.
【答案】C
【解析】
5.(分)(2015·日照)观察下列各式及其展开式:
,
,
,
,
请你猜想的展开式第三项的系数是(
).
A.
B.
C.
D.
【答案】B
【解析】
6.(分)计算:__________.
【答案】
【解析】
7.(分)(2016·南充)如果,且,那么的值是__________.
【答案】
【解析】
8.(分)先化简,再求值:,其中.
【答案】
【解析】解:原式,
把代入,
得原式.
9.(分)已知,求代数式的值.
【答案】
【解析】解:因为,所以.
因为原式,
,
所以原式.
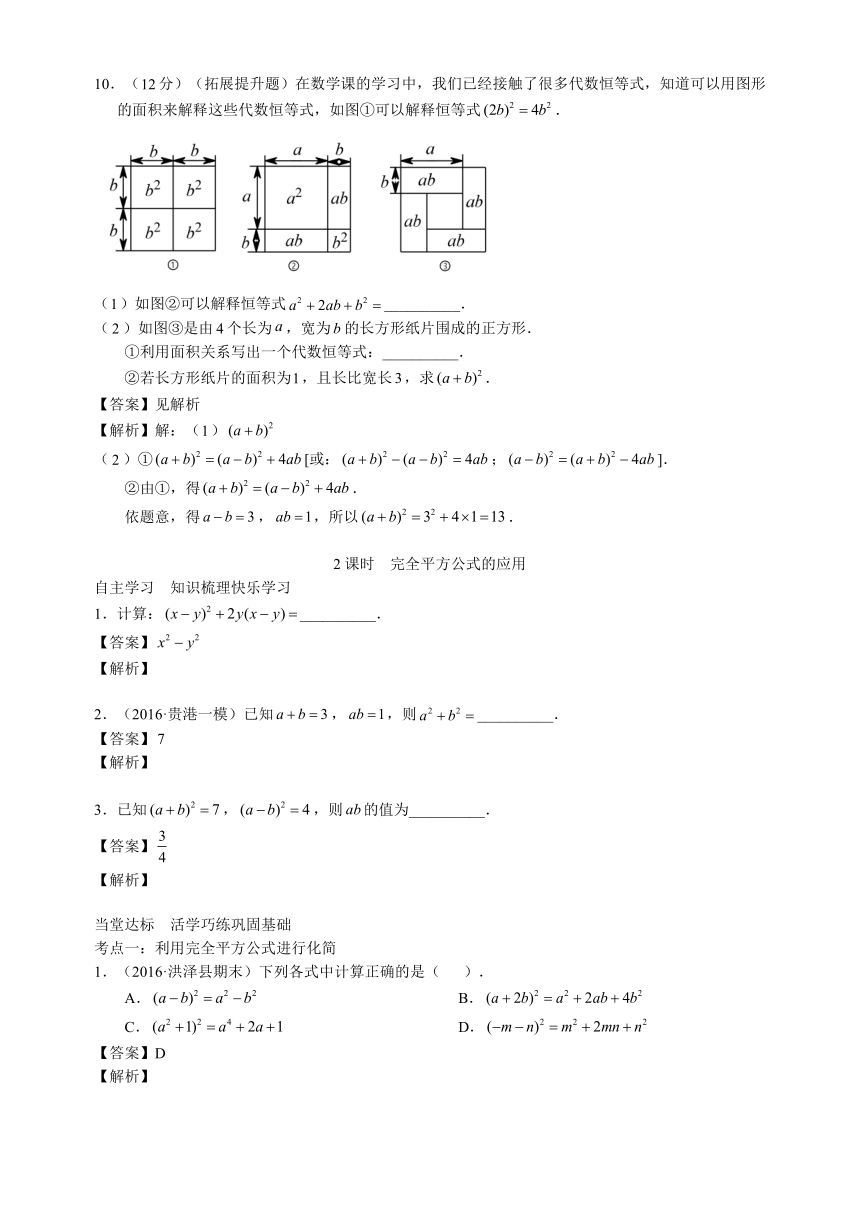
10.(分)(拓展提升题)在数学课的学习中,我们已经接触了很多代数恒等式,知道可以用图形的面积来解释这些代数恒等式,如图①可以解释恒等式.
()如图②可以解释恒等式__________.
()如图③是由个长为,宽为的长方形纸片围成的正方形.
①利用面积关系写出一个代数恒等式:__________.
②若长方形纸片的面积为,且长比宽长,求.
【答案】见解析
【解析】解:()
()①[或:;].
②由①,得.
依题意,得,,所以.
2课时
完全平方公式的应用
自主学习
知识梳理快乐学习
1.计算:__________.
【答案】
【解析】
2.(2016·贵港一模)已知,,则__________.
【答案】
【解析】
3.已知,,则的值为__________.
【答案】
【解析】
当堂达标
活学巧练巩固基础
考点一:利用完全平方公式进行化简
1.(2016·洪泽县期末)下列各式中计算正确的是(
).
A.
B.
C.
D.
【答案】D
【解析】
2.(2016·东平县期末)对于任意有理数,,现用“☆”定义一种运算:,根据这个定义,代数式可以化简为(
).
A.
B.
C.
D.
【答案】C
【解析】
3.(2016·宜春模拟)计算:__________.
【答案】
【解析】
考点二:利用完全平方公式求代数式的值
4.(2016·泰安市岱岳区期末)设,则(
).
A.
B.
C.
D.
【答案】B
【解析】
5.(一题多辨)()(2016·威海期中)若,则的值是(
).
A.
B.
C.
D.
()(2016·盐城校级期中)若,则的值为(
).
A.
B.
C.
D.无法确定
【答案】()C
()A
【解析】
6.(2016·重庆校级二模)已知,则代数式的值为(
).
A.
B.
C.
D.
【答案】C
【解析】
7.(2016·育才中学期末)若,,则的值为__________.
【答案】
【解析】
8.(2016·仙居县一模变式)已知,求的值.
【答案】
【解析】解:因为,
所以,
所以,
所以,
即,
所以.
考点三:利用完全平方公式进行简便计算
9.(2016·高密市期末)运用完全平方公式计算的最佳选择是(
).
A.
B.
C.
D.
【答案】C
【解析】
10.简便计算.
().
().
()(2016·福建校级月考变式).
【答案】见解析
【解析】解:()原式
.
()原式
.
()原式
.
考点四:完全平方公式的实际应用
11.(2016·宁波模拟)已知,,求的值,这个问题我们可以用边长分别为和的两种正方形组成一个图形来解决,其中,能较为简单地解决这个问题的图形是(
).
A.
B.
C.
D.
【答案】B
【解析】
12.(2016·市北区期末)如果一个正方形的面积是,则这个正方形的周长是多少?
【答案】
【解析】解:因为,,,
所以这个正方形的边长为,
所以这个正方形的周长是.
强化训练
综合演练强化能力
1.(分)(2016·雅安校级期中)运算结果是的是(
).
A.
B.
C.
D.
【答案】A
【解析】
2.(分)(2016·滕州市期中)已知,,则下列计算正确的是(
).
A.
B.
C.
D.
【答案】A
【解析】
3.(分)(2016·雅安校级期中)已知,则的值为(
).
A.
B.
C.
D.
【答案】C
【解析】
4.(分)(2016·寿光市期末)如图,通过计算大正方形的面积,可以验证一个等式,这个等式是(
).
A.
B.
C.
D.
【答案】C
【解析】
5.(分)(2016·新都区模拟)若,则__________.
【答案】
【解析】
6.(分)(2016·丹阳市期末)__________.
【答案】
【解析】
7.(分)(2016·泰兴市期末)若多项式加上一个含字母的单项式,就能变形为一个含的多项式的平方,则这样的单项式为__________.(数学思想链接:分类讨论思想)
【答案】或
【解析】
8.(分)(2016·慈溪市期末)已知,,则__________.
【答案】
【解析】
9.(分)(2016·宿州校级期末)利用一个的正方形,个的正方形,个的长方形,可拼成一个无缝隙且不重叠的大正方形,则这个大正方形的边长是__________.
【答案】
【解析】
10.(分)(2016·永登县期中)表示两个相邻整数的平均数的平方,表示这两个相邻整数平方和的平均数,试比较与的大小.(方法链接:作差法)
【答案】
【解析】解:设两个相邻整数分别为,,
则,.
因为,
所以.
11.(分)(拓展提升题)(2016·山西模拟)阅读与观察:
我国古代数学的许多发现都曾位居世界前列,如图①的“杨辉三角”就是其中的一例,杨辉,字谦光,南宋时期杭州人,在他所著的《详解九章算法》一书中,记录了如图①所示的三角形数表,称之为“开方作法本源”图,经观察研究发现,在两腰上的数为的前提下,“杨辉三角”有许多重要的特点,例如:每个数都等于它上方两数之和等等,
如图②,某同学发现“杨辉三角”给出了(为正整数)的展开式(按的次数由大到小的顺序排列)的系数规律.例如在三角形中第三行的三个数,,,恰好对应展开式中各项的系数;第四行的四个数,,,,恰好对应着展开式中各项的系数等等.
()通过观察,请你写出“杨辉三角”具有的任意两个特点.(阅读材料中的特点除外)
()计算:.
()请你直接写出的展开式.
【答案】见解析
【解析】()解:()第行有个数字,数字之和为.
().
().
乘法公式的六种应用技巧
一、直接应用
1.计算:
().
().
().
【答案】见解析
【解析】解:()原式.
()原式.
()原式.
2.计算.
().
().
【答案】见解析
【解析】解:()原式.
()原式.
二、变位应用
3.计算.
().
().
().
【答案】见解析
【解析】()解:()原式.
()原式.
()原式.
三、整体应用
4.计算.
().
().
【答案】见解析
【解析】解:()原式
.
()原式
.
四、连续应用
5.计算.
().
().
【答案】见解析
【解析】解:()原式.
()原式
.
五、逆向应用
6.计算.
().
().
【答案】见解析
【解析】解:()原式
.
()原式
.
7.已知,并且,求的值.
【答案】
【解析】解:因为,
所以,
所以,
即,
所以或,
所以或.
六、变形应用
8.用乘法公式计算.
().
().
().
【答案】见解析
【解析】解:()原式
.
()原式
.
()原式
.
9.计算.
().
().
().
【答案】见解析
【解析】解:()原式
.
()原式
.
()原式
.
10.已知:,,求:
()的值.
()的值.
()的值.
【答案】见解析
【解析】解:()
.
()
.
()
.
11.已知,,求的值.
【答案】
【解析】解:因为,,
所以①,
②,
所以①②,得,
所以.
所以.
12.已知,求的值.
【答案】
【解析】解:因为,
所以,
即,
所以,所以.
所以.
13.计算:.
【答案】
【解析】解:原式
.
完全平方公式
第1课时
完全平方公式
自主学习
知识梳理快乐学习
完全平方公式
两个数的和的平方等于这两个数的平方和与它们积的倍的和;两个数的差的平方等于这两个数的平方和与它们积的倍的差.用字母表示为:__________,__________.
【答案】
【解析】
当堂达标
活学巧练巩固基础
考点一:完全平方式的特征
1.计算结果是完全平方式的为(
).
A.
B.
C.
D.
【答案】C
【解析】
2.多项式加上一个单项式后能成为一个完全平方式,则加上的单项式不可以是(
).
A.
B.
C.
D.
【答案】D
【解析】
3.若是完全平方式,则等于(
).
A.
B.
C.
D.
【答案】A
【解析】
4.(2016·市北区期中)是完全平方式,则__________.(数学思想链接:分类讨论思想)
【答案】
【解析】
考点二:完全平方公式
5.下列多项式中,不能用完全平方公式计算的是(
).
A.
B.
C.
D.
【答案】D
【解析】
6.下列计算正确的是(
).
A.
B.
C.
D.
【答案】C
【解析】
7.下列式子错误的是(
).
A.
B.
C.
D.
【答案】D
【解析】
8.(一题多辨)()若,则为(
).
A.
B.
C.
D.
()已知,,则(
).
A.
B.
C.
D.
()已知有理数满足,则__________.
【答案】()C
()A
()
【解析】
9.运算结果为的是(
).
A.
B.
C.
D.
【答案】B
【解析】
10.如图,最大的正方形的面积是(
).
A.
B.
C.
D.
【答案】C
【解析】
11.__________.
【答案】
【解析】
12.计算.
().
().
()(2016·市北区期中).
【答案】见解析
【解析】()原式.
()原式.
()原式
.
13.(2016·常州)先化简,再求值:,其中.
【答案】见解析
【解析】解:原式,
,
,
当时,
原式.
强化训练
综合演练强化能力
1.(分)(2016·武汉)运用乘法公式计算的结果是(
).
A.
B.
C.
D.
【答案】C
【解析】
2.(分)(2016·育才中学期中)若,那么等于(
).
A.
B.
C.
D.
【答案】D
【解析】
3.(分)(一题多辨)()已知,,则的值为(
)(数学思想链接:整体思想)
A.
B.
C.
D.
()(2015·胶南市王台中学质检)若,,则__________.
【答案】()C
()
【解析】
4.(分)图①是一个长为,宽为的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四个形状和大小都一样的小长方形,然后按图②那样拼成一个正方形,则中间空的部分的面积是(
).
A.
B.
C.
D.
【答案】C
【解析】
5.(分)(2015·日照)观察下列各式及其展开式:
,
,
,
,
请你猜想的展开式第三项的系数是(
).
A.
B.
C.
D.
【答案】B
【解析】
6.(分)计算:__________.
【答案】
【解析】
7.(分)(2016·南充)如果,且,那么的值是__________.
【答案】
【解析】
8.(分)先化简,再求值:,其中.
【答案】
【解析】解:原式,
把代入,
得原式.
9.(分)已知,求代数式的值.
【答案】
【解析】解:因为,所以.
因为原式,
,
所以原式.
10.(分)(拓展提升题)在数学课的学习中,我们已经接触了很多代数恒等式,知道可以用图形的面积来解释这些代数恒等式,如图①可以解释恒等式.
()如图②可以解释恒等式__________.
()如图③是由个长为,宽为的长方形纸片围成的正方形.
①利用面积关系写出一个代数恒等式:__________.
②若长方形纸片的面积为,且长比宽长,求.
【答案】见解析
【解析】解:()
()①[或:;].
②由①,得.
依题意,得,,所以.
2课时
完全平方公式的应用
自主学习
知识梳理快乐学习
1.计算:__________.
【答案】
【解析】
2.(2016·贵港一模)已知,,则__________.
【答案】
【解析】
3.已知,,则的值为__________.
【答案】
【解析】
当堂达标
活学巧练巩固基础
考点一:利用完全平方公式进行化简
1.(2016·洪泽县期末)下列各式中计算正确的是(
).
A.
B.
C.
D.
【答案】D
【解析】
2.(2016·东平县期末)对于任意有理数,,现用“☆”定义一种运算:,根据这个定义,代数式可以化简为(
).
A.
B.
C.
D.
【答案】C
【解析】
3.(2016·宜春模拟)计算:__________.
【答案】
【解析】
考点二:利用完全平方公式求代数式的值
4.(2016·泰安市岱岳区期末)设,则(
).
A.
B.
C.
D.
【答案】B
【解析】
5.(一题多辨)()(2016·威海期中)若,则的值是(
).
A.
B.
C.
D.
()(2016·盐城校级期中)若,则的值为(
).
A.
B.
C.
D.无法确定
【答案】()C
()A
【解析】
6.(2016·重庆校级二模)已知,则代数式的值为(
).
A.
B.
C.
D.
【答案】C
【解析】
7.(2016·育才中学期末)若,,则的值为__________.
【答案】
【解析】
8.(2016·仙居县一模变式)已知,求的值.
【答案】
【解析】解:因为,
所以,
所以,
所以,
即,
所以.
考点三:利用完全平方公式进行简便计算
9.(2016·高密市期末)运用完全平方公式计算的最佳选择是(
).
A.
B.
C.
D.
【答案】C
【解析】
10.简便计算.
().
().
()(2016·福建校级月考变式).
【答案】见解析
【解析】解:()原式
.
()原式
.
()原式
.
考点四:完全平方公式的实际应用
11.(2016·宁波模拟)已知,,求的值,这个问题我们可以用边长分别为和的两种正方形组成一个图形来解决,其中,能较为简单地解决这个问题的图形是(
).
A.
B.
C.
D.
【答案】B
【解析】
12.(2016·市北区期末)如果一个正方形的面积是,则这个正方形的周长是多少?
【答案】
【解析】解:因为,,,
所以这个正方形的边长为,
所以这个正方形的周长是.
强化训练
综合演练强化能力
1.(分)(2016·雅安校级期中)运算结果是的是(
).
A.
B.
C.
D.
【答案】A
【解析】
2.(分)(2016·滕州市期中)已知,,则下列计算正确的是(
).
A.
B.
C.
D.
【答案】A
【解析】
3.(分)(2016·雅安校级期中)已知,则的值为(
).
A.
B.
C.
D.
【答案】C
【解析】
4.(分)(2016·寿光市期末)如图,通过计算大正方形的面积,可以验证一个等式,这个等式是(
).
A.
B.
C.
D.
【答案】C
【解析】
5.(分)(2016·新都区模拟)若,则__________.
【答案】
【解析】
6.(分)(2016·丹阳市期末)__________.
【答案】
【解析】
7.(分)(2016·泰兴市期末)若多项式加上一个含字母的单项式,就能变形为一个含的多项式的平方,则这样的单项式为__________.(数学思想链接:分类讨论思想)
【答案】或
【解析】
8.(分)(2016·慈溪市期末)已知,,则__________.
【答案】
【解析】
9.(分)(2016·宿州校级期末)利用一个的正方形,个的正方形,个的长方形,可拼成一个无缝隙且不重叠的大正方形,则这个大正方形的边长是__________.
【答案】
【解析】
10.(分)(2016·永登县期中)表示两个相邻整数的平均数的平方,表示这两个相邻整数平方和的平均数,试比较与的大小.(方法链接:作差法)
【答案】
【解析】解:设两个相邻整数分别为,,
则,.
因为,
所以.
11.(分)(拓展提升题)(2016·山西模拟)阅读与观察:
我国古代数学的许多发现都曾位居世界前列,如图①的“杨辉三角”就是其中的一例,杨辉,字谦光,南宋时期杭州人,在他所著的《详解九章算法》一书中,记录了如图①所示的三角形数表,称之为“开方作法本源”图,经观察研究发现,在两腰上的数为的前提下,“杨辉三角”有许多重要的特点,例如:每个数都等于它上方两数之和等等,
如图②,某同学发现“杨辉三角”给出了(为正整数)的展开式(按的次数由大到小的顺序排列)的系数规律.例如在三角形中第三行的三个数,,,恰好对应展开式中各项的系数;第四行的四个数,,,,恰好对应着展开式中各项的系数等等.
()通过观察,请你写出“杨辉三角”具有的任意两个特点.(阅读材料中的特点除外)
()计算:.
()请你直接写出的展开式.
【答案】见解析
【解析】()解:()第行有个数字,数字之和为.
().
().
乘法公式的六种应用技巧
一、直接应用
1.计算:
().
().
().
【答案】见解析
【解析】解:()原式.
()原式.
()原式.
2.计算.
().
().
【答案】见解析
【解析】解:()原式.
()原式.
二、变位应用
3.计算.
().
().
().
【答案】见解析
【解析】()解:()原式.
()原式.
()原式.
三、整体应用
4.计算.
().
().
【答案】见解析
【解析】解:()原式
.
()原式
.
四、连续应用
5.计算.
().
().
【答案】见解析
【解析】解:()原式.
()原式
.
五、逆向应用
6.计算.
().
().
【答案】见解析
【解析】解:()原式
.
()原式
.
7.已知,并且,求的值.
【答案】
【解析】解:因为,
所以,
所以,
即,
所以或,
所以或.
六、变形应用
8.用乘法公式计算.
().
().
().
【答案】见解析
【解析】解:()原式
.
()原式
.
()原式
.
9.计算.
().
().
().
【答案】见解析
【解析】解:()原式
.
()原式
.
()原式
.
10.已知:,,求:
()的值.
()的值.
()的值.
【答案】见解析
【解析】解:()
.
()
.
()
.
11.已知,,求的值.
【答案】
【解析】解:因为,,
所以①,
②,
所以①②,得,
所以.
所以.
12.已知,求的值.
【答案】
【解析】解:因为,
所以,
即,
所以,所以.
所以.
13.计算:.
【答案】
【解析】解:原式
.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
