14.2.2 完全平方公式课件(24张PPT)
文档属性
| 名称 | 14.2.2 完全平方公式课件(24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 817.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-05 22:17:46 | ||
图片预览






文档简介
(共24张PPT)
(a±b)2 =a2±2ab+b2
a2
ab
b2
财主土地
阿凡提土地
a
a
b
b
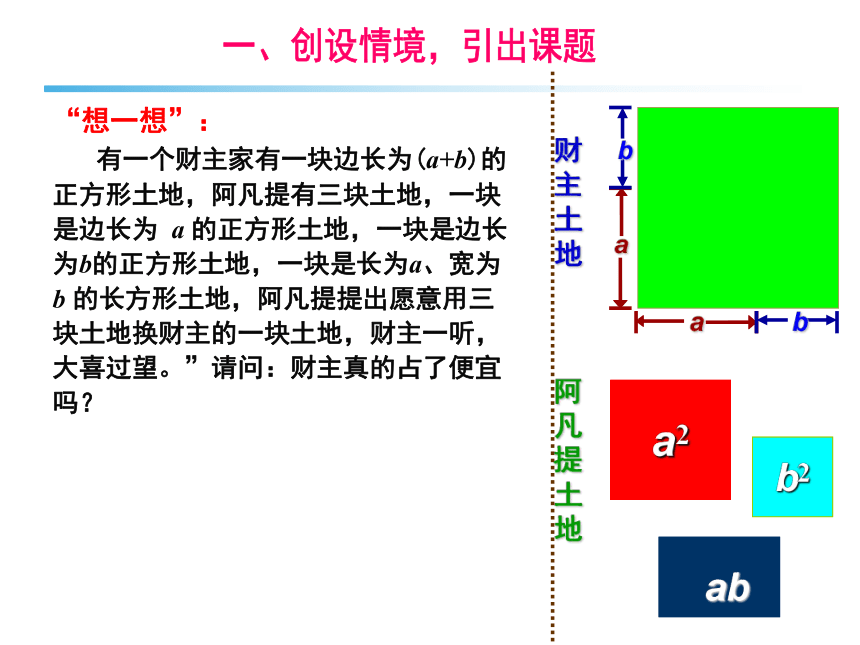
“想一想”: 有一个财主家有一块边长为(a+b)的正方形土地,阿凡提有三块土地,一块是边长为 a 的正方形土地,一块是边长为b的正方形土地,一块是长为a、宽为b 的长方形土地,阿凡提提出愿意用三块土地换财主的一块土地,财主一听,大喜过望。”请问:财主真的占了便宜吗?
a2
b2
ab
a
a
b
b
a2
ab
财主土地
阿凡提土地
a2
ab
b2
财主
多ab
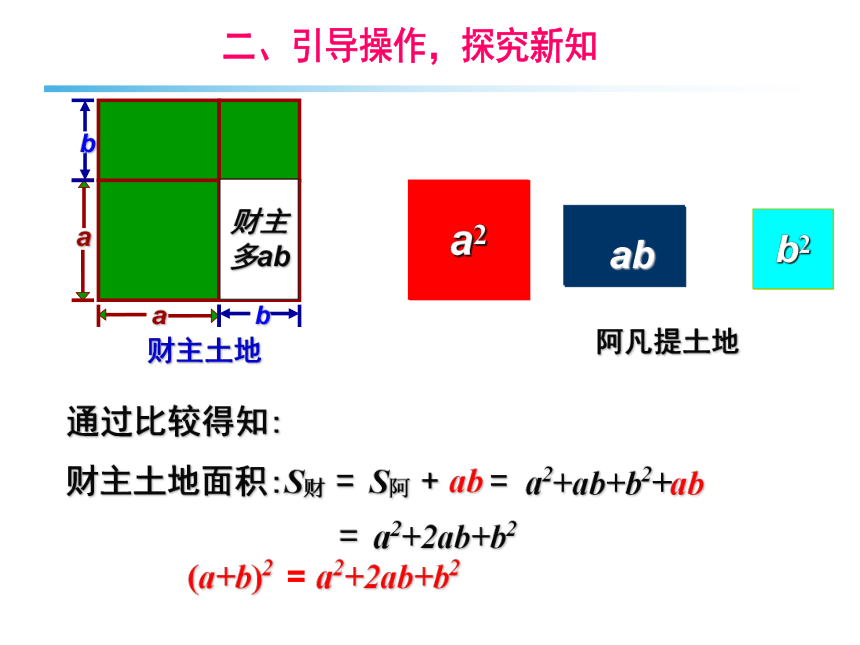
通过比较得知:
财主土地面积:S财 = S阿 + =
(a+b)2
ab
a2+ab+b2+ab
= a2+2ab+b2
b2
a2+2ab+b2
=
b
b
a
a
(a+b)
a
b
ab
ab
两数和的完全平方公式
(a+b)2 =
(a+b)2=
a2+ab+ab+b2
=a2+2ab+b2
= a2+ab+ab+b2
(a+b) (a+b)
=a2+2ab+b2
你能用多项式的乘法法则来进行证明吗?
(a b)2=
(a-b)2 =
= a2-ab-ab+b2
(a-b) (a-b)
=a2-2ab+b2
(a-b)2 =
= a2+2a(-b)+(-b)2
[(a+(-b)]2
=a2-2ab+b2
证明方法一:
证明方法二:
a
a
a
ab
ab
b
b
b
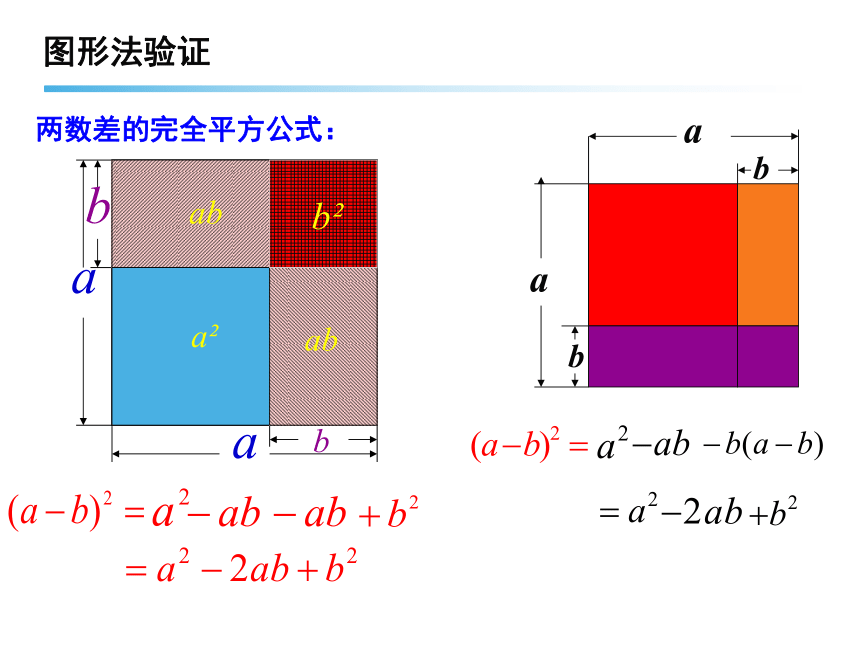
两数差的完全平方公式:
a
a
b
b
图形法验证
完全平方公式:
(a+b)
2
a + 2ab + b
2
2
=
(a-b)
2
a - 2ab + b
2
2
=
即:两数和的平方,等于它们的平方和,加它们的积的2倍。
公式的结构特征:
1、左边是一个二项式的完全平方的形式,
3、公式右边的符号特征:平方项的符号都是正的,
2、公式右边是一个三项式,
结构是:“首平方,尾平方,首尾积的二倍放中央”
中间一项的符号与左边运算符号一致。
两数差的平方,等于它们的平方和,减它们的积的2倍。
例1: 运用完全平方公式计算:
解: (4m+5)2 =
=16m2
(1) (4m+5)2
(a+b)2 = a2 + 2 a b + b2
(4m)2
+2 (4m) 5
+52
+40m
+25
=x2
解:(x 2y)2
(a b)2= a2 2 ab + b2
=x2
2 x (2y)
+(2y)2
4xy
+4y2
(2) (x 2y)2
解: ( 3m+9)2 =
=9m2
(3) ( 3m+9)2
(a + b)2 = a2 + 2 a b + b2
( 3m)2
+2 ( 3m) 9
+92
54m
+81
=9y2
解:(-3y-7)2
(a - b)2 = a2 - 2 ab + b2
=(-3y)2
-2 (-3y) 7
+72
+42y
+49
(4) (-3y-7)2
1.运用完全平方公式计算:
(1) (x 3)2
(2) ( 2a+1)2
(3) (2m+3)2
(4) ( 3y 1)2
随堂练习
(1)
=x2 2 x 3+9
=x2 6x+9
=( 2a)2+2 ( 2a) 1+1
=4a2 4a+1
= 4m2 +12m+9
=( 3y)2 2 ( 3y) 1+1
=9y2+6y+1
小明解的有误吗?
错误
注意:首项,未项平方要添括号
(1)
应改为: (-2a +3)2= (-2a)2+2 (-2a) 3+9
=4a2-12a+1
第一数被平方时, 未添括号;
第一数与第二数乘积的2倍 少乘了一个2;
小亮解的有误吗?
错误
注意:完全平方公式右边有三项,别忘了间项,“首尾乘积的2倍”
诊断
少了第一数与第二数乘积的2倍
(丢了一项);
(2)
应改为: (2m+5)2= (2m)2+2 (2m) 5 +25
=4m2+20m+25
小华解的有误吗?
错误
诊断
注意:首项,未项的符号都是正的,中间项的符号与前面运算符号一致
首项和中间项的符号错了
应改为: ( 3y 1)2=( 3y)2 2 ( 3y ) 1+12=9y2+6y+1
(-2m-3n)2=
(-2m)2
(2m+3n)2=
4m2
4m2-12mn+9n2
= 4m2+12mn+9n2
(2m-3n)2=
(-2m+3n)2=
(-2m)2+2 (-2m) (3n)+(3n)2
=4m2-12mn+9n2
①
②
③
④
+12mn
+9n2
+(3n)2
-2 (-2m) (3n)
观察 & 思考
活动三:
(-a-b)2 ___(a+b)2
两数和的完全平方公式
两数差的完全平方公式
=
=
议一议
=
你能用语言来描述我们发现的规律吗?
当所给的二项式的符号相反时,就用
当所给的二项式的符号相同时,就用
(-a+b)2 ___(b-a)2 ___(a-b)2
例2: 计算:(1) 10022 ; (2) 9992 .
完全平方公式(a ±b)2=a2 ±2ab+b2
观察 & 思考
把10022 改写成 (a+b)2 还是(a b)2
a、b怎样确定?
(1) 10022
= (1000+2)2
=1000000+4000+4
=1004004
例2: 计算:(1) 10022 ; (2) 9992 .
完全平方公式(a ±b)2=a2 ±2ab+b2
观察 & 思考
把9992 改写成 (a+b)2 还是(a b)2
a、b怎样确定?
(2) 9992
= (1000-1)2
=1000000-2000+1
=998001
3.(宁波·中考)若x+y=3, xy=1,则x2+y2=
2.如果x2+mx+4是一个完全平方式,则m=
1.将正方形的边长由acm增加6cm,则正方形的面 积增加了
随堂练习
(2)
学习了本节课,你有哪些收获?
(一起分享一下吧!)
共同
交流
(a b)2=a2 2ab+b2;
几种证明完全平方公式的方法:
几个重要的数学思想和方法
必做题:1、P112复习巩固第2题
2、P112综合运用第4题
思考题:
计算(1)(a+b+c)2
(2)(a+b)3
(a±b)2 =a2±2ab+b2
a2
ab
b2
财主土地
阿凡提土地
a
a
b
b
“想一想”: 有一个财主家有一块边长为(a+b)的正方形土地,阿凡提有三块土地,一块是边长为 a 的正方形土地,一块是边长为b的正方形土地,一块是长为a、宽为b 的长方形土地,阿凡提提出愿意用三块土地换财主的一块土地,财主一听,大喜过望。”请问:财主真的占了便宜吗?
a2
b2
ab
a
a
b
b
a2
ab
财主土地
阿凡提土地
a2
ab
b2
财主
多ab
通过比较得知:
财主土地面积:S财 = S阿 + =
(a+b)2
ab
a2+ab+b2+ab
= a2+2ab+b2
b2
a2+2ab+b2
=
b
b
a
a
(a+b)
a
b
ab
ab
两数和的完全平方公式
(a+b)2 =
(a+b)2=
a2+ab+ab+b2
=a2+2ab+b2
= a2+ab+ab+b2
(a+b) (a+b)
=a2+2ab+b2
你能用多项式的乘法法则来进行证明吗?
(a b)2=
(a-b)2 =
= a2-ab-ab+b2
(a-b) (a-b)
=a2-2ab+b2
(a-b)2 =
= a2+2a(-b)+(-b)2
[(a+(-b)]2
=a2-2ab+b2
证明方法一:
证明方法二:
a
a
a
ab
ab
b
b
b
两数差的完全平方公式:
a
a
b
b
图形法验证
完全平方公式:
(a+b)
2
a + 2ab + b
2
2
=
(a-b)
2
a - 2ab + b
2
2
=
即:两数和的平方,等于它们的平方和,加它们的积的2倍。
公式的结构特征:
1、左边是一个二项式的完全平方的形式,
3、公式右边的符号特征:平方项的符号都是正的,
2、公式右边是一个三项式,
结构是:“首平方,尾平方,首尾积的二倍放中央”
中间一项的符号与左边运算符号一致。
两数差的平方,等于它们的平方和,减它们的积的2倍。
例1: 运用完全平方公式计算:
解: (4m+5)2 =
=16m2
(1) (4m+5)2
(a+b)2 = a2 + 2 a b + b2
(4m)2
+2 (4m) 5
+52
+40m
+25
=x2
解:(x 2y)2
(a b)2= a2 2 ab + b2
=x2
2 x (2y)
+(2y)2
4xy
+4y2
(2) (x 2y)2
解: ( 3m+9)2 =
=9m2
(3) ( 3m+9)2
(a + b)2 = a2 + 2 a b + b2
( 3m)2
+2 ( 3m) 9
+92
54m
+81
=9y2
解:(-3y-7)2
(a - b)2 = a2 - 2 ab + b2
=(-3y)2
-2 (-3y) 7
+72
+42y
+49
(4) (-3y-7)2
1.运用完全平方公式计算:
(1) (x 3)2
(2) ( 2a+1)2
(3) (2m+3)2
(4) ( 3y 1)2
随堂练习
(1)
=x2 2 x 3+9
=x2 6x+9
=( 2a)2+2 ( 2a) 1+1
=4a2 4a+1
= 4m2 +12m+9
=( 3y)2 2 ( 3y) 1+1
=9y2+6y+1
小明解的有误吗?
错误
注意:首项,未项平方要添括号
(1)
应改为: (-2a +3)2= (-2a)2+2 (-2a) 3+9
=4a2-12a+1
第一数被平方时, 未添括号;
第一数与第二数乘积的2倍 少乘了一个2;
小亮解的有误吗?
错误
注意:完全平方公式右边有三项,别忘了间项,“首尾乘积的2倍”
诊断
少了第一数与第二数乘积的2倍
(丢了一项);
(2)
应改为: (2m+5)2= (2m)2+2 (2m) 5 +25
=4m2+20m+25
小华解的有误吗?
错误
诊断
注意:首项,未项的符号都是正的,中间项的符号与前面运算符号一致
首项和中间项的符号错了
应改为: ( 3y 1)2=( 3y)2 2 ( 3y ) 1+12=9y2+6y+1
(-2m-3n)2=
(-2m)2
(2m+3n)2=
4m2
4m2-12mn+9n2
= 4m2+12mn+9n2
(2m-3n)2=
(-2m+3n)2=
(-2m)2+2 (-2m) (3n)+(3n)2
=4m2-12mn+9n2
①
②
③
④
+12mn
+9n2
+(3n)2
-2 (-2m) (3n)
观察 & 思考
活动三:
(-a-b)2 ___(a+b)2
两数和的完全平方公式
两数差的完全平方公式
=
=
议一议
=
你能用语言来描述我们发现的规律吗?
当所给的二项式的符号相反时,就用
当所给的二项式的符号相同时,就用
(-a+b)2 ___(b-a)2 ___(a-b)2
例2: 计算:(1) 10022 ; (2) 9992 .
完全平方公式(a ±b)2=a2 ±2ab+b2
观察 & 思考
把10022 改写成 (a+b)2 还是(a b)2
a、b怎样确定?
(1) 10022
= (1000+2)2
=1000000+4000+4
=1004004
例2: 计算:(1) 10022 ; (2) 9992 .
完全平方公式(a ±b)2=a2 ±2ab+b2
观察 & 思考
把9992 改写成 (a+b)2 还是(a b)2
a、b怎样确定?
(2) 9992
= (1000-1)2
=1000000-2000+1
=998001
3.(宁波·中考)若x+y=3, xy=1,则x2+y2=
2.如果x2+mx+4是一个完全平方式,则m=
1.将正方形的边长由acm增加6cm,则正方形的面 积增加了
随堂练习
(2)
学习了本节课,你有哪些收获?
(一起分享一下吧!)
共同
交流
(a b)2=a2 2ab+b2;
几种证明完全平方公式的方法:
几个重要的数学思想和方法
必做题:1、P112复习巩固第2题
2、P112综合运用第4题
思考题:
计算(1)(a+b+c)2
(2)(a+b)3
