12.2 三角形全等的判定(第4课时)课件
文档属性
| 名称 | 12.2 三角形全等的判定(第4课时)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 227.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-08-28 21:55:55 | ||
图片预览


文档简介
课件14张PPT。
§11.2.4 三角形全等的判定2:我们已经学过判定全等三角形的方法有哪些?AB——DE
AC——DF
BC——EF
∠A——∠D
∠B——∠DEF
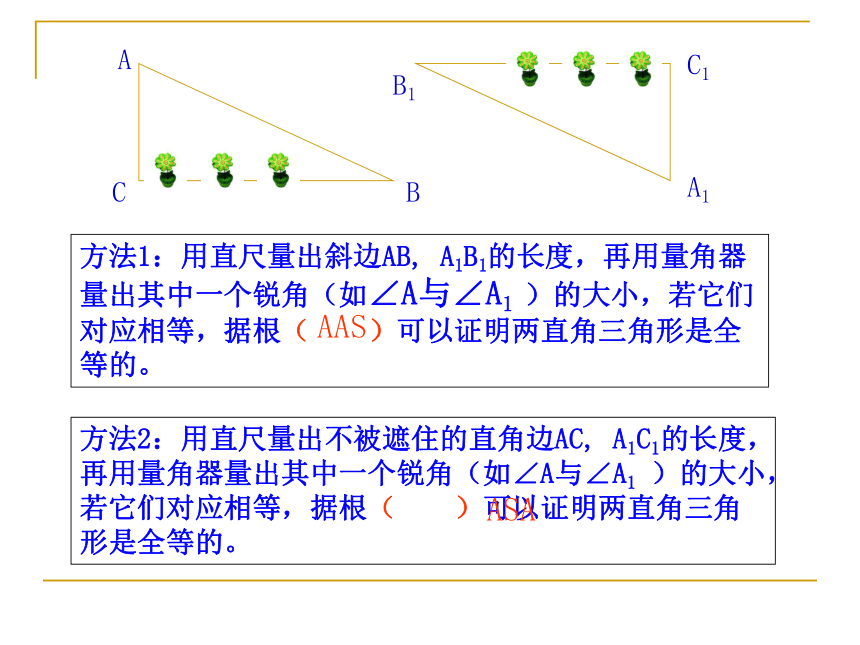
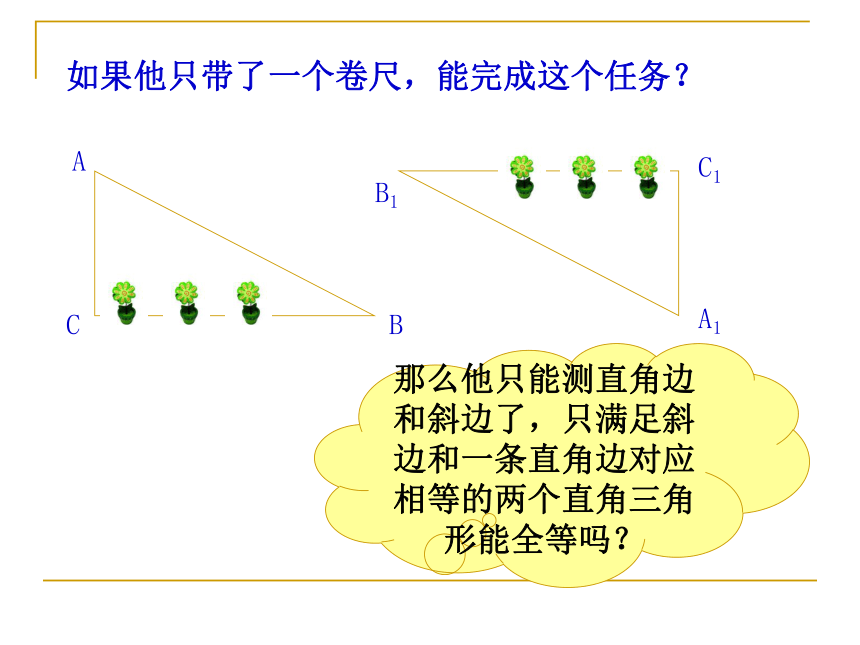
∠ACB——∠F(SSS)、(SAS)、(ASA)、(AAS)复习旧知 引入新知如图,舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但两个三角形都有一条直角边被花盆遮住无法测量.你能帮他想个办法吗?创设情景 引入课题方法1:用直尺量出斜边AB, A1B1的长度,再用量角器量出其中一个锐角(如∠A与∠A1 )的大小,若它们对应相等,据根( )可以证明两直角三角形是全等的。 方法2:用直尺量出不被遮住的直角边AC, A1C1的长度,再用量角器量出其中一个锐角(如∠A与∠A1 )的大小,若它们对应相等,据根( )可以证明两直角三角形是全等的。AAS ASA如果他只带了一个卷尺,能完成这个任务?
那么他只能测直角边和斜边了,只满足斜边和一条直角边对应相等的两个直角三角形能全等吗?画一画:
任意画一个Rt△ACB ,使∠C﹦90°,再画一个
Rt△A′C′B′使∠C﹦∠C′,B′C′﹦BC,A′B′﹦AB
(1):你能试着画出来吗?与小组交流一下。作法:
1、画∠MC′N=90°
2、在射线C′M上取B′C′=BC
3、以B′为圆心,AB为半径画弧,交射线C′N于点A′
4、连接A′B′,△A′C′B′就是所作三角形。(2):把画好的Rt△A′C′B′放到Rt△ACB上,
它们全等吗?你能发现什么规律?
动手实践 探索规律
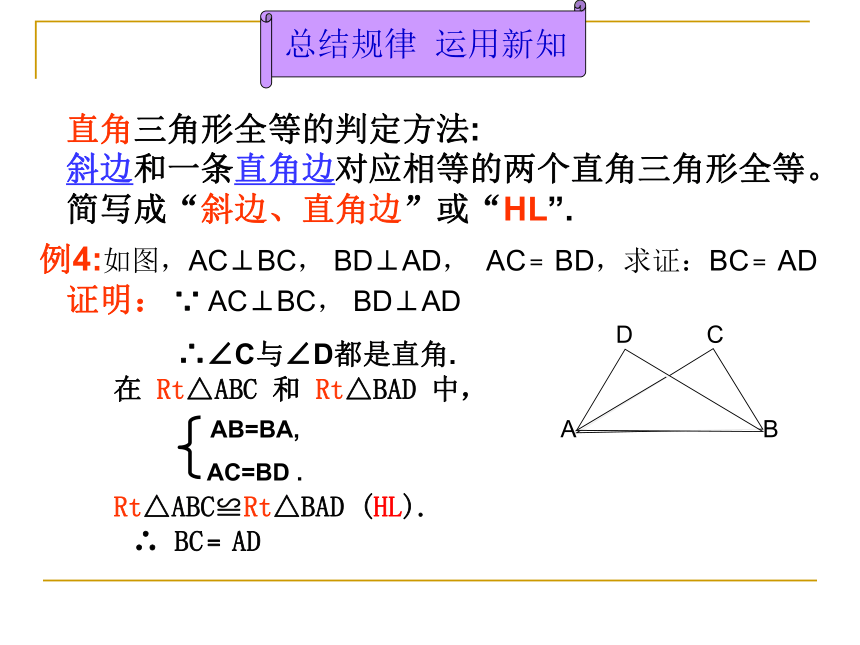
直角三角形全等的判定方法:
斜边和一条直角边对应相等的两个直角三角形全等。简写成“斜边、直角边”或“HL”.
证明: ∵ AC⊥BC, BD⊥AD
∴∠C与∠D都是直角.Rt△ABC≌Rt△BAD (HL).
∴ BC﹦AD
在 Rt△ABC 和 Rt△BAD 中,总结规律 运用新知如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF
求证:BF=DE巩固练习如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF
求证:BD平分EFG变式训练1如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF
想想:BD平分EF吗?C变式训练2议一议如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?∠ABC+∠DFE=90°联系实际 综合应用解:在Rt△ABC和Rt△DEF中∴ Rt△ABC≌Rt△DEF (HL).∴∠ABC=∠DEF
(全等三角形对应角相等).∵ ∠DEF+∠DFE=90°,∴∠ABC+∠DFE=90°1.直角三角形是特殊的三角形,所以不仅有一般三角形的判定全等的方法,而且还有直角三角形特殊的判定方法----“HL”
2.两个直角三角形中,由于有直角相等的隐含条件,所以只须找两个条件即可(两个条件中至少有一个条件是一对对应边相等)
书面作业:
课后体会:学完判定全等三角形的条件后,你 有什么收获?课后作业
§11.2.4 三角形全等的判定2:我们已经学过判定全等三角形的方法有哪些?AB——DE
AC——DF
BC——EF
∠A——∠D
∠B——∠DEF
∠ACB——∠F(SSS)、(SAS)、(ASA)、(AAS)复习旧知 引入新知如图,舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但两个三角形都有一条直角边被花盆遮住无法测量.你能帮他想个办法吗?创设情景 引入课题方法1:用直尺量出斜边AB, A1B1的长度,再用量角器量出其中一个锐角(如∠A与∠A1 )的大小,若它们对应相等,据根( )可以证明两直角三角形是全等的。 方法2:用直尺量出不被遮住的直角边AC, A1C1的长度,再用量角器量出其中一个锐角(如∠A与∠A1 )的大小,若它们对应相等,据根( )可以证明两直角三角形是全等的。AAS ASA如果他只带了一个卷尺,能完成这个任务?
那么他只能测直角边和斜边了,只满足斜边和一条直角边对应相等的两个直角三角形能全等吗?画一画:
任意画一个Rt△ACB ,使∠C﹦90°,再画一个
Rt△A′C′B′使∠C﹦∠C′,B′C′﹦BC,A′B′﹦AB
(1):你能试着画出来吗?与小组交流一下。作法:
1、画∠MC′N=90°
2、在射线C′M上取B′C′=BC
3、以B′为圆心,AB为半径画弧,交射线C′N于点A′
4、连接A′B′,△A′C′B′就是所作三角形。(2):把画好的Rt△A′C′B′放到Rt△ACB上,
它们全等吗?你能发现什么规律?
动手实践 探索规律
直角三角形全等的判定方法:
斜边和一条直角边对应相等的两个直角三角形全等。简写成“斜边、直角边”或“HL”.
证明: ∵ AC⊥BC, BD⊥AD
∴∠C与∠D都是直角.Rt△ABC≌Rt△BAD (HL).
∴ BC﹦AD
在 Rt△ABC 和 Rt△BAD 中,总结规律 运用新知如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF
求证:BF=DE巩固练习如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF
求证:BD平分EFG变式训练1如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF
想想:BD平分EF吗?C变式训练2议一议如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?∠ABC+∠DFE=90°联系实际 综合应用解:在Rt△ABC和Rt△DEF中∴ Rt△ABC≌Rt△DEF (HL).∴∠ABC=∠DEF
(全等三角形对应角相等).∵ ∠DEF+∠DFE=90°,∴∠ABC+∠DFE=90°1.直角三角形是特殊的三角形,所以不仅有一般三角形的判定全等的方法,而且还有直角三角形特殊的判定方法----“HL”
2.两个直角三角形中,由于有直角相等的隐含条件,所以只须找两个条件即可(两个条件中至少有一个条件是一对对应边相等)
书面作业:
课后体会:学完判定全等三角形的条件后,你 有什么收获?课后作业
