江苏省盐城市2016-2017学年高二下学期期末数学试卷(文科)Word版含解析
文档属性
| 名称 | 江苏省盐城市2016-2017学年高二下学期期末数学试卷(文科)Word版含解析 |  | |
| 格式 | zip | ||
| 文件大小 | 296.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-08-31 08:59:49 | ||
图片预览




文档简介
www.
2016-2017学年江苏省盐城市高二(下)期末数学试卷(文科)
一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.
1.已知复数(i是虚数单位),则|z|=
.
2.已知命题p:“ n∈N
,使得
n2<2n”,则命题¬p的真假为
.
3.设θ∈R,则“sinθ=0”是“sin2θ=0”的
条件.(选填:充分不必要、必要不充分、充要、既不充分也不必要)
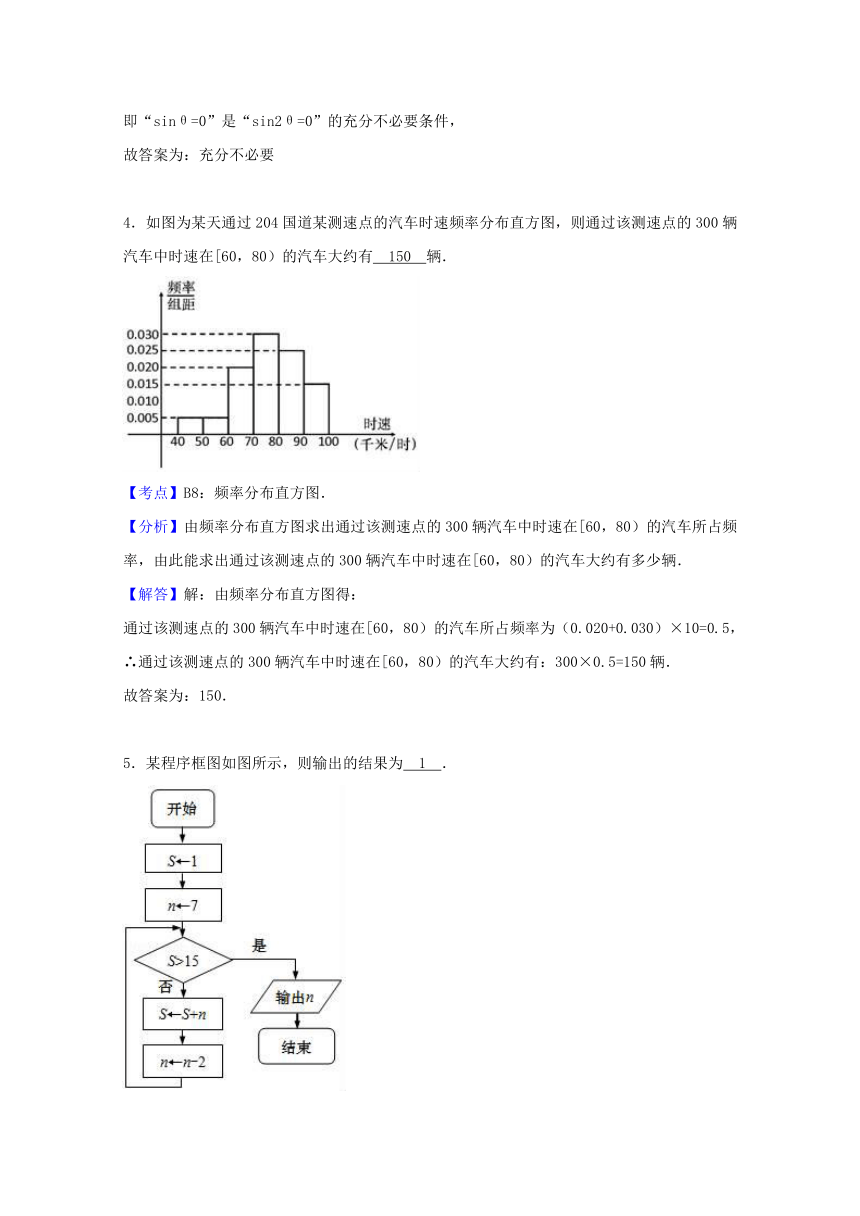
4.如图为某天通过204国道某测速点的汽车时速频率分布直方图,则通过该测速点的300辆汽车中时速在[60,80)的汽车大约有
辆.
5.某程序框图如图所示,则输出的结果为
.
6.在区间(0,5)上随机取一个实数x,则x满足x2﹣2x<0的概率为
.
7.已知双曲线﹣=1(a>0)的渐近线方程是y=±x,则其准线方程为
.
8.若函数f(x)=在区间(0,2)上有极值,则a的取值范围是
.
9.已知函数f(x)=x3,则不等式f(2x)+f(x﹣1)<0的解集是
.
10.将函数f(x)=sin(2x+)的图象向右平移m个单位(m>0),若所得图象对应的函数为偶函数,则m的最小值是
.
11.已知圆x2+y2=r2(r>0)的内接四边形的面积的最大值为2r2,类比可得椭圆+=1(a>b>0)的内接四边形的面积的最大值为
.
12.已知集合M={(x,y)|}和集合N={(x,y)|y=sinx,x≥0},若M∩N≠ ,则实数a的最大值为
.
13.已知点F是椭圆C:
+=1(a>b>0)的左焦点,若椭圆C上存在两点P、Q满足=2,则椭圆C的离心率的取值范围是
.
14.已知a>0,b>0,0<c<2,ac2+b﹣c=0,则+的取值范围是
.
二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.已知关于x的不等式ax2+(a﹣2)x﹣2≥0,其中a∈R.
(1)若不等式的解集为(﹣∞,﹣1]∪[4,+∞),求实数a的值;
(2)若不等式ax2+(a﹣2)x﹣2≥2x2﹣5对任意实数x恒成立,求实数a的取值范围.
16.已知函数f(x)=x+sinx.x∈(﹣,),函数g(x)的定义域为实数集R,函数h(x)=f(x)+g(x),
(1)若函数g(x)是奇函数,判断并证明函数h(x)的奇偶性;
(2)若函数g(x)是单调增函数,用反证法证明函数h(x)的图象与x轴至多有一个交点.
17.已知函数f(x)=cosxcos(x+).
(1)求f(x)在区间[0,]上的值域;
(2)若f(θ)=,﹣<θ<,求cos2θ的值.
18.如图所示,矩形ABCD为本市沿海的一块滩涂湿地,其中阴影区域有丹顶鹤活动,曲线AC是以AD所在直线为对称轴的抛物线的一部分,其中AB=1km,BC=2km,现准备开发一个面积为0.6km2的湿地公园,要求不能破坏丹顶鹤活动区域.问:能否在AB边上取点E、在BC边上取点F,使得△BEF区域满足该项目的用地要求?若能,请给出点E、F的选址方案;若不能,请说明理由.
19.在平面直角坐标系xOy内,椭圆E:
+=1(a>b>0),离心率为,右焦点F到右准线的距离为2,直线l过右焦点F且与椭圆E交于A、B两点.
(1)求椭圆E的标准方程;
(2)若直线l与x轴垂直,C为椭圆E上的动点,求CA2+CB2的取值范围;
(3)若动直线l与x轴不重合,在x轴上是否存在定点P,使得PF始终平分∠APB?若存在,请求出点P的坐标;若不存在,请说明理由.
20.已知函数f(x)=ex和函数g(x)=kx+m(k、m为实数,e为自然对数的底数,e≈2.71828).
(1)求函数h(x)=f(x)﹣g(x)的单调区间;
(2)当k=2,m=1时,判断方程f(x)=g(x)的实数根的个数并证明;
(3)已知m≠1,不等式(m﹣1)[f(x)﹣g(x)]≤0对任意实数x恒成立,求km的最大值.
2016-2017学年江苏省盐城市高二(下)期末数学试卷(文科)
参考答案与试题解析
一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.
1.已知复数(i是虚数单位),则|z|= 1 .
【考点】A8:复数求模.
【分析】首先进行复数的除法运算,分子和分母同乘以分母的共轭复数,整理成最简形式,是一个纯虚数,求出模长.
【解答】解:
==,
∴|z|=1,
故答案为:1
2.已知命题p:“ n∈N
,使得
n2<2n”,则命题¬p的真假为 假 .
【考点】2J:命题的否定.
【分析】根据特称命题的否定是全称命题,再判断真假即可
【解答】解:命题是特称命题,则命题的否定是“ n∈N,n2≥2n”,
当n=1时不成立.
故¬p为假命题,
故答案为:假.
3.设θ∈R,则“sinθ=0”是“sin2θ=0”的 充分不必要 条件.(选填:充分不必要、必要不充分、充要、既不充分也不必要)
【考点】2L:必要条件、充分条件与充要条件的判断.
【分析】根据充分条件和必要条件的定义,结合三角函数的倍角公式进行判断即可.
【解答】解:当sinθ=0时,sin2θ=2sinθcosθ=0成立,即充分性成立,
当cosθ=0,sinθ≠0时,满足sin2θ=2sinθcosθ=0,但sinθ=0不成立,即必要性不成立,
即“sinθ=0”是“sin2θ=0”的充分不必要条件,
故答案为:充分不必要
4.如图为某天通过204国道某测速点的汽车时速频率分布直方图,则通过该测速点的300辆汽车中时速在[60,80)的汽车大约有 150 辆.
【考点】B8:频率分布直方图.
【分析】由频率分布直方图求出通过该测速点的300辆汽车中时速在[60,80)的汽车所占频率,由此能求出通过该测速点的300辆汽车中时速在[60,80)的汽车大约有多少辆.
【解答】解:由频率分布直方图得:
通过该测速点的300辆汽车中时速在[60,80)的汽车所占频率为(0.020+0.030)×10=0.5,
∴通过该测速点的300辆汽车中时速在[60,80)的汽车大约有:300×0.5=150辆.
故答案为:150.
5.某程序框图如图所示,则输出的结果为 1 .
【考点】EF:程序框图.
【分析】由已知中的程序语句可知:该程序的功能是利用循环结构计算变量S的值并输出对应的n的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.
【解答】解:模拟程序的运行,可得
S=1,n=7
不满足条件S>15,执行循环体,S=8,n=5
不满足条件S>15,执行循环体,S=13,n=3
不满足条件S>15,执行循环体,S=16,n=1
满足条件S>15,退出循环,输出n的值为1.
故答案为:1.
6.在区间(0,5)上随机取一个实数x,则x满足x2﹣2x<0的概率为 .
【考点】CF:几何概型.
【分析】求解一元二次不等式得x2﹣2x<0的解集,再由长度比求出x2﹣2x<0的概率.
【解答】解:由x2﹣2x<0,得0<x<2.
∴不等式x2﹣2x<0的解集为(0,2).
则在区间(0,5)上随机取一个实数x,则x满足x2﹣2x<0的概率为.
故答案为:.
7.已知双曲线﹣=1(a>0)的渐近线方程是y=±x,则其准线方程为 x=± .
【考点】KC:双曲线的简单性质.
【分析】根据题意,由双曲线的方程可得其渐近线方程,由题意分析可得a的值,由双曲线的几何性质可得c的值,进而将a、c的值代入双曲线的准线方程计算可得答案.
【解答】解:根据题意,双曲线的方程为﹣=1,其渐近线方程为y=±x,
又由该双曲线﹣=1的渐近线方程是y=±x,
则有=,
解可得a=3,
其中c==5,
则其准线方程为x=±,
故答案为:x=±.
8.若函数f(x)=在区间(0,2)上有极值,则a的取值范围是 (﹣1,1) .
【考点】6D:利用导数研究函数的极值.
【分析】求出函数的导数,求出函数的极值点,得到关于a的不等式,解出即可.
【解答】解:f′(x)=,
令f′(x)>0,解得:x<a+1,
令f′(x)<0,解得:x>a+1,
故f(x)在(﹣∞,a+1)递增,在(a+1,+∞)递减,
故x=a+1是函数的极大值点,
由题意得:0<a+1<2,解得:﹣1<a<1,
故答案为:(﹣1,1).
9.已知函数f(x)=x3,则不等式f(2x)+f(x﹣1)<0的解集是 (﹣∞,) .
【考点】3N:奇偶性与单调性的综合.
【分析】根据题意,由函数的解析式分析可得f(x)为奇函数且在R上递增,则不等式f(2x)+f(x﹣1)<0可以转化为2x<1﹣x,解可得x的取值范围,即可得答案.
【解答】解:根据题意,函数f(x)=x3,f(﹣x)=(﹣x)3=﹣x3,
即有f(﹣x)=﹣f(x),为奇函数;
f(x)=x3,其导数f′(x)=3x2≥0,为增函数;
则f(2x)+f(x﹣1)<0 f(2x)<﹣f(x﹣1) f(2x)<f(1﹣x) 2x<1﹣x,
解可得x<,
即不等式f(2x)+f(x﹣1)<0的解集为(﹣∞,);
故答案为:(﹣∞,).
10.将函数f(x)=sin(2x+)的图象向右平移m个单位(m>0),若所得图象对应的函数为偶函数,则m的最小值是 .
【考点】HJ:函数y=Asin(ωx+φ)的图象变换.
【分析】利用函数y=Asin(ωx+φ)的图象变换规律,三角函数的图象的奇偶性,求得m的最小正值.
【解答】解:将函数f(x)=sin(2x+)的图象向右平移m个单位(m>0),可得y=sin[2(x﹣m)+]=sin(2x﹣2m+),
若所得图象对应的函数为偶函数,则﹣2m+=kπ+,k∈Z,即m=﹣﹣,
则m的最小正值为,
故答案为:.
11.已知圆x2+y2=r2(r>0)的内接四边形的面积的最大值为2r2,类比可得椭圆+=1(a>b>0)的内接四边形的面积的最大值为 2ab .
【考点】F3:类比推理.
【分析】将圆的方程转化为+=1,类比猜测椭圆+=1(a>b>0)的内接四边形的面积的最大值即可.
【解答】解:将圆的方程转化为+=1,
圆x2+y2=r2(r>0)的内接四边形的面积的最大值为2r2,
类比可得椭圆+=1(a>b>0)的内接四边形的面积的最大值为2ab,
故答案为:2ab.
12.已知集合M={(x,y)|}和集合N={(x,y)|y=sinx,x≥0},若M∩N≠ ,则实数a的最大值为 ﹣ .
【考点】6H:利用导数研究曲线上某点切线方程;7C:简单线性规划.
【分析】作出函数y=sinx(x≥0)的图象,以及不等式组表示的可行域,由直线x﹣2y+a=0与y=sinx相切时,设切点为(m,sinm),求出导数和直线的斜率,解方程可得切点和此时a的值,由图象可得a的最大值.
【解答】解:作出函数y=sinx(x≥0)的图象,
以及不等式组表示的可行域,
当直线x﹣2y+a=0与y=sinx相切时,设切点为(m,sinm),
即有cosm=,解得m=,
切点为(,),
可得a=2×﹣=﹣,
由题意可得a≤﹣,即有M∩N≠ ,
可得a的最大值为﹣,
故答案为:﹣.
13.已知点F是椭圆C:
+=1(a>b>0)的左焦点,若椭圆C上存在两点P、Q满足=2,则椭圆C的离心率的取值范围是 [,1) .
【考点】KL:直线与椭圆的位置关系.
【分析】设P((x1,y1),Q(x2,y2),F(﹣c,0),直线PQ:y=k(x+c),可得y1=﹣2y2.
由,得(b2+a2k2)y2﹣2kcb2y﹣b4k2=0
…②,…③
由①②③得b2+a2k2=8c2, 8c2≥b2=a2﹣c2 9c2≥a2即可求解
【解答】解:设P((x1,y1),Q(x2,y2),F(﹣c,0),直线PF:y=k(x+c).
∵P、Q满足=2,∴y1=﹣2y2…①
由,得(b2+a2k2)y2﹣2kcb2y﹣b4k2=0
…②,…③
由①②得,代入③得
b2+a2k2=8c2, 8c2≥b2=a2﹣c2 9c2≥a2
,∴椭圆C的离心率的取值范围是[,1)
故答案为[,1)
14.已知a>0,b>0,0<c<2,ac2+b﹣c=0,则+的取值范围是 [4,+∞) .
【考点】7F:基本不等式.
【分析】利用基本不等式的性质即可得出.
【解答】解:a>0,b>0,0<c<2,ac2+b﹣c=0,
∴1=ac+≥2,当ac=时,等号成立,
∴ab≤,
∵+≥2≥2=4,当a=b时等号成立,此时c=1∈(0,2),
综上所述,
+的取值范围是[4,+∞),
故答案为:[4,+∞)
二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.已知关于x的不等式ax2+(a﹣2)x﹣2≥0,其中a∈R.
(1)若不等式的解集为(﹣∞,﹣1]∪[4,+∞),求实数a的值;
(2)若不等式ax2+(a﹣2)x﹣2≥2x2﹣5对任意实数x恒成立,求实数a的取值范围.
【考点】3R:函数恒成立问题;74:一元二次不等式的解法.
【分析】(1)由题意知1,4是方程ax2+(a﹣2)x﹣2=0的解,利用韦达定理即可求得实数a的值;
(2)不等式ax2+(a﹣2)x﹣2≥2x2﹣5对任意实数x恒成立,可化为(a﹣2)x2+(a﹣2)x+3≥0对任意实数x∈R恒成立,分a=2与a≠2两类讨论,即可求得实数a的取值范围.
【解答】(文科)解:(1)由题意知方程ax2+(a﹣2)x﹣2=0的解为﹣1,4,且a>0,…
所以﹣=﹣4,解得a=.…
(2)问题可化为(a﹣2)x2+(a﹣2)x+3≥0对任意实数x∈R恒成立,
①当a=2时,3≥0恒成立;
…
②当a≠2时,,解得2<a≤14;…
综上①②得2≤a≤14.…
16.已知函数f(x)=x+sinx.x∈(﹣,),函数g(x)的定义域为实数集R,函数h(x)=f(x)+g(x),
(1)若函数g(x)是奇函数,判断并证明函数h(x)的奇偶性;
(2)若函数g(x)是单调增函数,用反证法证明函数h(x)的图象与x轴至多有一个交点.
【考点】3L:函数奇偶性的性质;3K:函数奇偶性的判断.
【分析】(1)先判断f(x)的奇偶性,再计算h(﹣x)与h(x)的关系得出结论;
(2)假设h(x)的图象与x轴至少有两个交点,不妨设两交点横坐标为x1,x2,且x1<x2,则h(x1)=h(x2),于是(x2)﹣g(x1)=f(x1)﹣f(x2),根据f(x)的单调性得出g(x)的单调性,从而得出矛盾.
【解答】解:(1)h(x)是奇函数,证明如下:
∵f(﹣x)=﹣x+sin(﹣x)=﹣x﹣sinx=﹣f(x),
∴f(x)是奇函数,
又g(x)是奇函数,∴g(﹣x)=﹣g(x),
∴h(﹣x)=f(﹣x)+g(﹣x)=﹣f(x)﹣g(x)=﹣h(x),
∴h(x)是奇函数.
(2)假设h(x)的图象与x轴至少有两个交点,不妨设两交点横坐标为x1,x2,且x1<x2,
则h(x1)=h(x2)=0,
即f(x1)+g(x1)=f(x2)+g(x2),∴g(x2)﹣g(x1)=f(x1)﹣f(x2)=(x1﹣x2)+(sinx1﹣sinx2),
∵x1,x2∈(0,),且x1<x2,
∴x1﹣x2<0,sinx1﹣sinx2<0
∴(x1﹣x2)+(sinx1﹣sinx2)<0,即g(x2)﹣g(x1)<0,
∴g(x1)>g(x2),
∴g(x)是减函数,与g(x)是增函数矛盾,
∴假设不成立,即函数h(x)的图象与x轴至多有一个交点.
17.已知函数f(x)=cosxcos(x+).
(1)求f(x)在区间[0,]上的值域;
(2)若f(θ)=,﹣<θ<,求cos2θ的值.
【考点】GL:三角函数中的恒等变换应用;H2:正弦函数的图象.
【分析】(1)化函数f(x)为余弦型函数,根据x∈[0,]时求出f(x)的值域即可;
(2)由f(θ)求出cos(2θ+)的值,利用cos2θ=cos[(2θ+)﹣]求出三角函数值即可.
【解答】解:(1)函数f(x)=cosxcos(x+)
=cosx(cosxcos﹣sinxsin)
=cos2x﹣sinxcosx
=(1+cos2x)﹣sin2x
=(cos2x﹣sin2x)+
=cos(2x+)+;
当x∈[0,]时,2x∈[0,π],
2x+∈[,],
∴cos(2x+)∈[﹣1,],
∴cos(2x+)+∈[﹣,],
∴f(x)在区间[0,]上的值域为[﹣,];
(2)f(θ)=cos(2θ+)+=,
∴cos(2θ+)=
﹣<θ<,∴0<2θ+<π
∴sin(2θ+)==
∴cos2θ=cos[(2θ+)﹣]
=cos(2θ+)cos+sin(2θ+)sin
=×﹣×
=.
18.如图所示,矩形ABCD为本市沿海的一块滩涂湿地,其中阴影区域有丹顶鹤活动,曲线AC是以AD所在直线为对称轴的抛物线的一部分,其中AB=1km,BC=2km,现准备开发一个面积为0.6km2的湿地公园,要求不能破坏丹顶鹤活动区域.问:能否在AB边上取点E、在BC边上取点F,使得△BEF区域满足该项目的用地要求?若能,请给出点E、F的选址方案;若不能,请说明理由.
【考点】K9:抛物线的应用.
【分析】由题意可得:△BEF区域满足该项目的用地要求等价于△BEF面积的最大值不小于0.6
km2,以A为原点,AB所在直线为x轴,AD所在直线为y轴,建立如图所示平面直角坐标系,求出A,B,C,D的坐标,运用待定系数法求出曲线AC的方程,欲使得△BEF的面积最大,必有EF与抛物线弧AC相切,设出切点(t,2t2),0≤t≤1,
求出导数,可得切线的斜率和方程,求出三角形BEF的面积,设f(t)=t3﹣2t2+2t,0<t≤1,求出导数和单调区间,可得极值,且为最值,即可判断是否满足要求.
【解答】解:△BEF区域满足该项目的用地要求等价于△BEF面积的最大值不小于0.6
km2,
以A为原点,AB所在直线为x轴,
AD所在直线为y轴,
建立如图所示平面直角坐标系,
则A(0,0),B(1,0),C(1,2),D(0,2),
设曲线AC所在的抛物线的方程为x2=2py(p>0),
代入点C(1,2)得p=,
得曲线AC的方程为y=2x2(0≤x≤1),
欲使得△BEF的面积最大,必有EF与抛物线弧AC相切,
设切点为P(t,2t2),0≤t≤1,
由y=2x2得y′=4x,故点P(t,2t2)处切线的斜率为4t,
切线的方程为y﹣2t2=4t(x﹣t),
即y=4tx﹣2t2,
当t=0时显然不合题意,故0<t≤1,
令x=1得yP=4t﹣2t2,令y=0得xK=t,
则S△BEF=BE BF=(1﹣)(4t﹣2t2)=t3﹣2t2+2t,
设f(t)=t3﹣2t2+2t,0<t≤1,
则f′(t)=(3t﹣2)(t﹣2),
令f′(t)>0得0<t<,令f′(t)<0得<t≤1,
故f(t)在(0,)上递增,在(,1]上递减,
故f(t)max=f()=,
而<0.6,故该方案所得△BEF区域不能满足该项目的用地要求.
19.在平面直角坐标系xOy内,椭圆E:
+=1(a>b>0),离心率为,右焦点F到右准线的距离为2,直线l过右焦点F且与椭圆E交于A、B两点.
(1)求椭圆E的标准方程;
(2)若直线l与x轴垂直,C为椭圆E上的动点,求CA2+CB2的取值范围;
(3)若动直线l与x轴不重合,在x轴上是否存在定点P,使得PF始终平分∠APB?若存在,请求出点P的坐标;若不存在,请说明理由.
【考点】KL:直线与椭圆的位置关系.
【分析】(1)由题意得:,得a,b即可
(2)A(2,),B(2,﹣),设点C(x0,y0),则CA2+CB2=(x0﹣2)2+(y0﹣)2+(x0﹣2)2+(y0+)2=2x02+2y02﹣8x0+12,又点C在椭圆上,∴,消去y0得CA2+CB2=,,即可求解.
(3)假设在x轴上存在点P满足题意,不妨设P(t,0),设A(x1,y1),B(x2,y2),由PF平分∠APB知:kAP+kBP=0,又kAP+kBP===0,利用韦达定理即可求解.
【解答】解:(1)由题意得:,得a=2,c=2,…
∵a2=b2+c2,∴b2=4,∴椭圆的标准方程为:.…
(2)当直线AB与x轴垂直时,A(2,),B(2,﹣),设点C(x0,y0),
则CA2+CB2=(x0﹣2)2+(y0﹣)2+(x0﹣2)2+(y0+)2=2x02+2y02﹣8x0+12,
又点C在椭圆上,∴,消去y0得CA2+CB2=,,
∴CA2+CB2得取值范围为[28﹣16,28+16].…
(3)假设在x轴上存在点P满足题意,不妨设P(t,0),设A(x1,y1),B(x2,y2),
设直线AB的方程为:x=my+2,联列,消去x得(m2+2)y2+4my﹣4=0,
则,,…
由PF平分∠APB知:kAP+kBP=0,…
又kAP+kBP===0,
又x1=my1+2,x2=my2+t,得(2﹣t)(y1+y2)+2my1y2=0,
即(2﹣t)×+2m×=0,得t=4,
所以存在点P(4,0)满足题意.
…
20.已知函数f(x)=ex和函数g(x)=kx+m(k、m为实数,e为自然对数的底数,e≈2.71828).
(1)求函数h(x)=f(x)﹣g(x)的单调区间;
(2)当k=2,m=1时,判断方程f(x)=g(x)的实数根的个数并证明;
(3)已知m≠1,不等式(m﹣1)[f(x)﹣g(x)]≤0对任意实数x恒成立,求km的最大值.
【考点】6E:利用导数求闭区间上函数的最值;6B:利用导数研究函数的单调性.
【分析】(1)求出h′(x)=ex﹣k,(x∈R),分以下两种情况讨论:①当k≤0,②当k>0,
(2)当k=2,m=1时,方程f(x)=g(x)即为h(x)=ex﹣2x﹣1=0,结合(1)及图象即可判定.
(3)设h(x)=f(x)﹣g(x),分①当m>1,②当m<1,分别求解
【解答】解:(1)h′(x)=ex﹣k,(x∈R),
①当k≤0时,h′(x)>0恒成立,h(x)的单调递增区间为(﹣∞,+∞),无单调递减区间;
②当k>0时,由h′(x)>0得x>lnk,由h′(x)<0得x<lnk,
故h(x)的单调递减区间为(﹣∞,lnk),单调递增区间为(lnk,+∞).
(2)当k=2,m=1时,方程f(x)=g(x)即为h(x)=ex﹣2x﹣1=0,
由(1)知h(x)在(﹣∞,ln2)上递减,而h(0)=0,故h(x)在(﹣∞,ln2)上有且仅有1个零点,
由(1)知h(x)在[ln2,+∞)上递增,而h(1)=e﹣3<0,h(2)=e2﹣5>0,且h(x)的图象在[1,2]上是连续不间断的,
故h(x)在[1,2]上有且仅有1个零点,所以h(x)在[ln2,+∞)上也有且仅有1个零点,
综上,方程f(x)=g(x)有且仅有两个实数根.
(3)设h(x)=f(x)﹣g(x),
①当m>1时,f(x)﹣g(x)≤0恒成立,则h(x)≤0恒成立,
而h(﹣)=e>0,与h(x)≤0恒成立矛盾,故m>1不合题意;
②当m<1时,f(x)﹣g(x)≥0,恒成立,则h(x)≥0恒成立,
1°当k=0时,由h(x)=ex﹣m≥0恒成立可得m∈(﹣∞,0],km=0;
2°当k<0时,h()=e﹣1,而,故e<1,
故h()<0,与h(x)≥0恒成立矛盾,故k<0不合题意;
3°当k>0时,由(1)可知[h(x)]min=h(lnk)=k﹣klnk﹣m,而h(x)≥0恒成立,
故k﹣klnk﹣m≥0,得m≤k﹣klnk,故km≤k(k﹣klnk),
记φ(k)=k(k﹣klnk),(k>0),
则φ′(k)=k(1﹣2lnk),由φ′(k)>0得0,由φ′(k)<0得k>,
故φ(k)在(0,)上单调递增,在(,+∞)上单调递减,
∴φ(k)max=φ()=,∴km≤,当且仅当k=,m=时取等号;
综上①②两种情况得km的最大值为.
2016-2017学年江苏省盐城市高二(下)期末数学试卷(文科)
一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.
1.已知复数(i是虚数单位),则|z|=
.
2.已知命题p:“ n∈N
,使得
n2<2n”,则命题¬p的真假为
.
3.设θ∈R,则“sinθ=0”是“sin2θ=0”的
条件.(选填:充分不必要、必要不充分、充要、既不充分也不必要)
4.如图为某天通过204国道某测速点的汽车时速频率分布直方图,则通过该测速点的300辆汽车中时速在[60,80)的汽车大约有
辆.
5.某程序框图如图所示,则输出的结果为
.
6.在区间(0,5)上随机取一个实数x,则x满足x2﹣2x<0的概率为
.
7.已知双曲线﹣=1(a>0)的渐近线方程是y=±x,则其准线方程为
.
8.若函数f(x)=在区间(0,2)上有极值,则a的取值范围是
.
9.已知函数f(x)=x3,则不等式f(2x)+f(x﹣1)<0的解集是
.
10.将函数f(x)=sin(2x+)的图象向右平移m个单位(m>0),若所得图象对应的函数为偶函数,则m的最小值是
.
11.已知圆x2+y2=r2(r>0)的内接四边形的面积的最大值为2r2,类比可得椭圆+=1(a>b>0)的内接四边形的面积的最大值为
.
12.已知集合M={(x,y)|}和集合N={(x,y)|y=sinx,x≥0},若M∩N≠ ,则实数a的最大值为
.
13.已知点F是椭圆C:
+=1(a>b>0)的左焦点,若椭圆C上存在两点P、Q满足=2,则椭圆C的离心率的取值范围是
.
14.已知a>0,b>0,0<c<2,ac2+b﹣c=0,则+的取值范围是
.
二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.已知关于x的不等式ax2+(a﹣2)x﹣2≥0,其中a∈R.
(1)若不等式的解集为(﹣∞,﹣1]∪[4,+∞),求实数a的值;
(2)若不等式ax2+(a﹣2)x﹣2≥2x2﹣5对任意实数x恒成立,求实数a的取值范围.
16.已知函数f(x)=x+sinx.x∈(﹣,),函数g(x)的定义域为实数集R,函数h(x)=f(x)+g(x),
(1)若函数g(x)是奇函数,判断并证明函数h(x)的奇偶性;
(2)若函数g(x)是单调增函数,用反证法证明函数h(x)的图象与x轴至多有一个交点.
17.已知函数f(x)=cosxcos(x+).
(1)求f(x)在区间[0,]上的值域;
(2)若f(θ)=,﹣<θ<,求cos2θ的值.
18.如图所示,矩形ABCD为本市沿海的一块滩涂湿地,其中阴影区域有丹顶鹤活动,曲线AC是以AD所在直线为对称轴的抛物线的一部分,其中AB=1km,BC=2km,现准备开发一个面积为0.6km2的湿地公园,要求不能破坏丹顶鹤活动区域.问:能否在AB边上取点E、在BC边上取点F,使得△BEF区域满足该项目的用地要求?若能,请给出点E、F的选址方案;若不能,请说明理由.
19.在平面直角坐标系xOy内,椭圆E:
+=1(a>b>0),离心率为,右焦点F到右准线的距离为2,直线l过右焦点F且与椭圆E交于A、B两点.
(1)求椭圆E的标准方程;
(2)若直线l与x轴垂直,C为椭圆E上的动点,求CA2+CB2的取值范围;
(3)若动直线l与x轴不重合,在x轴上是否存在定点P,使得PF始终平分∠APB?若存在,请求出点P的坐标;若不存在,请说明理由.
20.已知函数f(x)=ex和函数g(x)=kx+m(k、m为实数,e为自然对数的底数,e≈2.71828).
(1)求函数h(x)=f(x)﹣g(x)的单调区间;
(2)当k=2,m=1时,判断方程f(x)=g(x)的实数根的个数并证明;
(3)已知m≠1,不等式(m﹣1)[f(x)﹣g(x)]≤0对任意实数x恒成立,求km的最大值.
2016-2017学年江苏省盐城市高二(下)期末数学试卷(文科)
参考答案与试题解析
一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.
1.已知复数(i是虚数单位),则|z|= 1 .
【考点】A8:复数求模.
【分析】首先进行复数的除法运算,分子和分母同乘以分母的共轭复数,整理成最简形式,是一个纯虚数,求出模长.
【解答】解:
==,
∴|z|=1,
故答案为:1
2.已知命题p:“ n∈N
,使得
n2<2n”,则命题¬p的真假为 假 .
【考点】2J:命题的否定.
【分析】根据特称命题的否定是全称命题,再判断真假即可
【解答】解:命题是特称命题,则命题的否定是“ n∈N,n2≥2n”,
当n=1时不成立.
故¬p为假命题,
故答案为:假.
3.设θ∈R,则“sinθ=0”是“sin2θ=0”的 充分不必要 条件.(选填:充分不必要、必要不充分、充要、既不充分也不必要)
【考点】2L:必要条件、充分条件与充要条件的判断.
【分析】根据充分条件和必要条件的定义,结合三角函数的倍角公式进行判断即可.
【解答】解:当sinθ=0时,sin2θ=2sinθcosθ=0成立,即充分性成立,
当cosθ=0,sinθ≠0时,满足sin2θ=2sinθcosθ=0,但sinθ=0不成立,即必要性不成立,
即“sinθ=0”是“sin2θ=0”的充分不必要条件,
故答案为:充分不必要
4.如图为某天通过204国道某测速点的汽车时速频率分布直方图,则通过该测速点的300辆汽车中时速在[60,80)的汽车大约有 150 辆.
【考点】B8:频率分布直方图.
【分析】由频率分布直方图求出通过该测速点的300辆汽车中时速在[60,80)的汽车所占频率,由此能求出通过该测速点的300辆汽车中时速在[60,80)的汽车大约有多少辆.
【解答】解:由频率分布直方图得:
通过该测速点的300辆汽车中时速在[60,80)的汽车所占频率为(0.020+0.030)×10=0.5,
∴通过该测速点的300辆汽车中时速在[60,80)的汽车大约有:300×0.5=150辆.
故答案为:150.
5.某程序框图如图所示,则输出的结果为 1 .
【考点】EF:程序框图.
【分析】由已知中的程序语句可知:该程序的功能是利用循环结构计算变量S的值并输出对应的n的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.
【解答】解:模拟程序的运行,可得
S=1,n=7
不满足条件S>15,执行循环体,S=8,n=5
不满足条件S>15,执行循环体,S=13,n=3
不满足条件S>15,执行循环体,S=16,n=1
满足条件S>15,退出循环,输出n的值为1.
故答案为:1.
6.在区间(0,5)上随机取一个实数x,则x满足x2﹣2x<0的概率为 .
【考点】CF:几何概型.
【分析】求解一元二次不等式得x2﹣2x<0的解集,再由长度比求出x2﹣2x<0的概率.
【解答】解:由x2﹣2x<0,得0<x<2.
∴不等式x2﹣2x<0的解集为(0,2).
则在区间(0,5)上随机取一个实数x,则x满足x2﹣2x<0的概率为.
故答案为:.
7.已知双曲线﹣=1(a>0)的渐近线方程是y=±x,则其准线方程为 x=± .
【考点】KC:双曲线的简单性质.
【分析】根据题意,由双曲线的方程可得其渐近线方程,由题意分析可得a的值,由双曲线的几何性质可得c的值,进而将a、c的值代入双曲线的准线方程计算可得答案.
【解答】解:根据题意,双曲线的方程为﹣=1,其渐近线方程为y=±x,
又由该双曲线﹣=1的渐近线方程是y=±x,
则有=,
解可得a=3,
其中c==5,
则其准线方程为x=±,
故答案为:x=±.
8.若函数f(x)=在区间(0,2)上有极值,则a的取值范围是 (﹣1,1) .
【考点】6D:利用导数研究函数的极值.
【分析】求出函数的导数,求出函数的极值点,得到关于a的不等式,解出即可.
【解答】解:f′(x)=,
令f′(x)>0,解得:x<a+1,
令f′(x)<0,解得:x>a+1,
故f(x)在(﹣∞,a+1)递增,在(a+1,+∞)递减,
故x=a+1是函数的极大值点,
由题意得:0<a+1<2,解得:﹣1<a<1,
故答案为:(﹣1,1).
9.已知函数f(x)=x3,则不等式f(2x)+f(x﹣1)<0的解集是 (﹣∞,) .
【考点】3N:奇偶性与单调性的综合.
【分析】根据题意,由函数的解析式分析可得f(x)为奇函数且在R上递增,则不等式f(2x)+f(x﹣1)<0可以转化为2x<1﹣x,解可得x的取值范围,即可得答案.
【解答】解:根据题意,函数f(x)=x3,f(﹣x)=(﹣x)3=﹣x3,
即有f(﹣x)=﹣f(x),为奇函数;
f(x)=x3,其导数f′(x)=3x2≥0,为增函数;
则f(2x)+f(x﹣1)<0 f(2x)<﹣f(x﹣1) f(2x)<f(1﹣x) 2x<1﹣x,
解可得x<,
即不等式f(2x)+f(x﹣1)<0的解集为(﹣∞,);
故答案为:(﹣∞,).
10.将函数f(x)=sin(2x+)的图象向右平移m个单位(m>0),若所得图象对应的函数为偶函数,则m的最小值是 .
【考点】HJ:函数y=Asin(ωx+φ)的图象变换.
【分析】利用函数y=Asin(ωx+φ)的图象变换规律,三角函数的图象的奇偶性,求得m的最小正值.
【解答】解:将函数f(x)=sin(2x+)的图象向右平移m个单位(m>0),可得y=sin[2(x﹣m)+]=sin(2x﹣2m+),
若所得图象对应的函数为偶函数,则﹣2m+=kπ+,k∈Z,即m=﹣﹣,
则m的最小正值为,
故答案为:.
11.已知圆x2+y2=r2(r>0)的内接四边形的面积的最大值为2r2,类比可得椭圆+=1(a>b>0)的内接四边形的面积的最大值为 2ab .
【考点】F3:类比推理.
【分析】将圆的方程转化为+=1,类比猜测椭圆+=1(a>b>0)的内接四边形的面积的最大值即可.
【解答】解:将圆的方程转化为+=1,
圆x2+y2=r2(r>0)的内接四边形的面积的最大值为2r2,
类比可得椭圆+=1(a>b>0)的内接四边形的面积的最大值为2ab,
故答案为:2ab.
12.已知集合M={(x,y)|}和集合N={(x,y)|y=sinx,x≥0},若M∩N≠ ,则实数a的最大值为 ﹣ .
【考点】6H:利用导数研究曲线上某点切线方程;7C:简单线性规划.
【分析】作出函数y=sinx(x≥0)的图象,以及不等式组表示的可行域,由直线x﹣2y+a=0与y=sinx相切时,设切点为(m,sinm),求出导数和直线的斜率,解方程可得切点和此时a的值,由图象可得a的最大值.
【解答】解:作出函数y=sinx(x≥0)的图象,
以及不等式组表示的可行域,
当直线x﹣2y+a=0与y=sinx相切时,设切点为(m,sinm),
即有cosm=,解得m=,
切点为(,),
可得a=2×﹣=﹣,
由题意可得a≤﹣,即有M∩N≠ ,
可得a的最大值为﹣,
故答案为:﹣.
13.已知点F是椭圆C:
+=1(a>b>0)的左焦点,若椭圆C上存在两点P、Q满足=2,则椭圆C的离心率的取值范围是 [,1) .
【考点】KL:直线与椭圆的位置关系.
【分析】设P((x1,y1),Q(x2,y2),F(﹣c,0),直线PQ:y=k(x+c),可得y1=﹣2y2.
由,得(b2+a2k2)y2﹣2kcb2y﹣b4k2=0
…②,…③
由①②③得b2+a2k2=8c2, 8c2≥b2=a2﹣c2 9c2≥a2即可求解
【解答】解:设P((x1,y1),Q(x2,y2),F(﹣c,0),直线PF:y=k(x+c).
∵P、Q满足=2,∴y1=﹣2y2…①
由,得(b2+a2k2)y2﹣2kcb2y﹣b4k2=0
…②,…③
由①②得,代入③得
b2+a2k2=8c2, 8c2≥b2=a2﹣c2 9c2≥a2
,∴椭圆C的离心率的取值范围是[,1)
故答案为[,1)
14.已知a>0,b>0,0<c<2,ac2+b﹣c=0,则+的取值范围是 [4,+∞) .
【考点】7F:基本不等式.
【分析】利用基本不等式的性质即可得出.
【解答】解:a>0,b>0,0<c<2,ac2+b﹣c=0,
∴1=ac+≥2,当ac=时,等号成立,
∴ab≤,
∵+≥2≥2=4,当a=b时等号成立,此时c=1∈(0,2),
综上所述,
+的取值范围是[4,+∞),
故答案为:[4,+∞)
二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.已知关于x的不等式ax2+(a﹣2)x﹣2≥0,其中a∈R.
(1)若不等式的解集为(﹣∞,﹣1]∪[4,+∞),求实数a的值;
(2)若不等式ax2+(a﹣2)x﹣2≥2x2﹣5对任意实数x恒成立,求实数a的取值范围.
【考点】3R:函数恒成立问题;74:一元二次不等式的解法.
【分析】(1)由题意知1,4是方程ax2+(a﹣2)x﹣2=0的解,利用韦达定理即可求得实数a的值;
(2)不等式ax2+(a﹣2)x﹣2≥2x2﹣5对任意实数x恒成立,可化为(a﹣2)x2+(a﹣2)x+3≥0对任意实数x∈R恒成立,分a=2与a≠2两类讨论,即可求得实数a的取值范围.
【解答】(文科)解:(1)由题意知方程ax2+(a﹣2)x﹣2=0的解为﹣1,4,且a>0,…
所以﹣=﹣4,解得a=.…
(2)问题可化为(a﹣2)x2+(a﹣2)x+3≥0对任意实数x∈R恒成立,
①当a=2时,3≥0恒成立;
…
②当a≠2时,,解得2<a≤14;…
综上①②得2≤a≤14.…
16.已知函数f(x)=x+sinx.x∈(﹣,),函数g(x)的定义域为实数集R,函数h(x)=f(x)+g(x),
(1)若函数g(x)是奇函数,判断并证明函数h(x)的奇偶性;
(2)若函数g(x)是单调增函数,用反证法证明函数h(x)的图象与x轴至多有一个交点.
【考点】3L:函数奇偶性的性质;3K:函数奇偶性的判断.
【分析】(1)先判断f(x)的奇偶性,再计算h(﹣x)与h(x)的关系得出结论;
(2)假设h(x)的图象与x轴至少有两个交点,不妨设两交点横坐标为x1,x2,且x1<x2,则h(x1)=h(x2),于是(x2)﹣g(x1)=f(x1)﹣f(x2),根据f(x)的单调性得出g(x)的单调性,从而得出矛盾.
【解答】解:(1)h(x)是奇函数,证明如下:
∵f(﹣x)=﹣x+sin(﹣x)=﹣x﹣sinx=﹣f(x),
∴f(x)是奇函数,
又g(x)是奇函数,∴g(﹣x)=﹣g(x),
∴h(﹣x)=f(﹣x)+g(﹣x)=﹣f(x)﹣g(x)=﹣h(x),
∴h(x)是奇函数.
(2)假设h(x)的图象与x轴至少有两个交点,不妨设两交点横坐标为x1,x2,且x1<x2,
则h(x1)=h(x2)=0,
即f(x1)+g(x1)=f(x2)+g(x2),∴g(x2)﹣g(x1)=f(x1)﹣f(x2)=(x1﹣x2)+(sinx1﹣sinx2),
∵x1,x2∈(0,),且x1<x2,
∴x1﹣x2<0,sinx1﹣sinx2<0
∴(x1﹣x2)+(sinx1﹣sinx2)<0,即g(x2)﹣g(x1)<0,
∴g(x1)>g(x2),
∴g(x)是减函数,与g(x)是增函数矛盾,
∴假设不成立,即函数h(x)的图象与x轴至多有一个交点.
17.已知函数f(x)=cosxcos(x+).
(1)求f(x)在区间[0,]上的值域;
(2)若f(θ)=,﹣<θ<,求cos2θ的值.
【考点】GL:三角函数中的恒等变换应用;H2:正弦函数的图象.
【分析】(1)化函数f(x)为余弦型函数,根据x∈[0,]时求出f(x)的值域即可;
(2)由f(θ)求出cos(2θ+)的值,利用cos2θ=cos[(2θ+)﹣]求出三角函数值即可.
【解答】解:(1)函数f(x)=cosxcos(x+)
=cosx(cosxcos﹣sinxsin)
=cos2x﹣sinxcosx
=(1+cos2x)﹣sin2x
=(cos2x﹣sin2x)+
=cos(2x+)+;
当x∈[0,]时,2x∈[0,π],
2x+∈[,],
∴cos(2x+)∈[﹣1,],
∴cos(2x+)+∈[﹣,],
∴f(x)在区间[0,]上的值域为[﹣,];
(2)f(θ)=cos(2θ+)+=,
∴cos(2θ+)=
﹣<θ<,∴0<2θ+<π
∴sin(2θ+)==
∴cos2θ=cos[(2θ+)﹣]
=cos(2θ+)cos+sin(2θ+)sin
=×﹣×
=.
18.如图所示,矩形ABCD为本市沿海的一块滩涂湿地,其中阴影区域有丹顶鹤活动,曲线AC是以AD所在直线为对称轴的抛物线的一部分,其中AB=1km,BC=2km,现准备开发一个面积为0.6km2的湿地公园,要求不能破坏丹顶鹤活动区域.问:能否在AB边上取点E、在BC边上取点F,使得△BEF区域满足该项目的用地要求?若能,请给出点E、F的选址方案;若不能,请说明理由.
【考点】K9:抛物线的应用.
【分析】由题意可得:△BEF区域满足该项目的用地要求等价于△BEF面积的最大值不小于0.6
km2,以A为原点,AB所在直线为x轴,AD所在直线为y轴,建立如图所示平面直角坐标系,求出A,B,C,D的坐标,运用待定系数法求出曲线AC的方程,欲使得△BEF的面积最大,必有EF与抛物线弧AC相切,设出切点(t,2t2),0≤t≤1,
求出导数,可得切线的斜率和方程,求出三角形BEF的面积,设f(t)=t3﹣2t2+2t,0<t≤1,求出导数和单调区间,可得极值,且为最值,即可判断是否满足要求.
【解答】解:△BEF区域满足该项目的用地要求等价于△BEF面积的最大值不小于0.6
km2,
以A为原点,AB所在直线为x轴,
AD所在直线为y轴,
建立如图所示平面直角坐标系,
则A(0,0),B(1,0),C(1,2),D(0,2),
设曲线AC所在的抛物线的方程为x2=2py(p>0),
代入点C(1,2)得p=,
得曲线AC的方程为y=2x2(0≤x≤1),
欲使得△BEF的面积最大,必有EF与抛物线弧AC相切,
设切点为P(t,2t2),0≤t≤1,
由y=2x2得y′=4x,故点P(t,2t2)处切线的斜率为4t,
切线的方程为y﹣2t2=4t(x﹣t),
即y=4tx﹣2t2,
当t=0时显然不合题意,故0<t≤1,
令x=1得yP=4t﹣2t2,令y=0得xK=t,
则S△BEF=BE BF=(1﹣)(4t﹣2t2)=t3﹣2t2+2t,
设f(t)=t3﹣2t2+2t,0<t≤1,
则f′(t)=(3t﹣2)(t﹣2),
令f′(t)>0得0<t<,令f′(t)<0得<t≤1,
故f(t)在(0,)上递增,在(,1]上递减,
故f(t)max=f()=,
而<0.6,故该方案所得△BEF区域不能满足该项目的用地要求.
19.在平面直角坐标系xOy内,椭圆E:
+=1(a>b>0),离心率为,右焦点F到右准线的距离为2,直线l过右焦点F且与椭圆E交于A、B两点.
(1)求椭圆E的标准方程;
(2)若直线l与x轴垂直,C为椭圆E上的动点,求CA2+CB2的取值范围;
(3)若动直线l与x轴不重合,在x轴上是否存在定点P,使得PF始终平分∠APB?若存在,请求出点P的坐标;若不存在,请说明理由.
【考点】KL:直线与椭圆的位置关系.
【分析】(1)由题意得:,得a,b即可
(2)A(2,),B(2,﹣),设点C(x0,y0),则CA2+CB2=(x0﹣2)2+(y0﹣)2+(x0﹣2)2+(y0+)2=2x02+2y02﹣8x0+12,又点C在椭圆上,∴,消去y0得CA2+CB2=,,即可求解.
(3)假设在x轴上存在点P满足题意,不妨设P(t,0),设A(x1,y1),B(x2,y2),由PF平分∠APB知:kAP+kBP=0,又kAP+kBP===0,利用韦达定理即可求解.
【解答】解:(1)由题意得:,得a=2,c=2,…
∵a2=b2+c2,∴b2=4,∴椭圆的标准方程为:.…
(2)当直线AB与x轴垂直时,A(2,),B(2,﹣),设点C(x0,y0),
则CA2+CB2=(x0﹣2)2+(y0﹣)2+(x0﹣2)2+(y0+)2=2x02+2y02﹣8x0+12,
又点C在椭圆上,∴,消去y0得CA2+CB2=,,
∴CA2+CB2得取值范围为[28﹣16,28+16].…
(3)假设在x轴上存在点P满足题意,不妨设P(t,0),设A(x1,y1),B(x2,y2),
设直线AB的方程为:x=my+2,联列,消去x得(m2+2)y2+4my﹣4=0,
则,,…
由PF平分∠APB知:kAP+kBP=0,…
又kAP+kBP===0,
又x1=my1+2,x2=my2+t,得(2﹣t)(y1+y2)+2my1y2=0,
即(2﹣t)×+2m×=0,得t=4,
所以存在点P(4,0)满足题意.
…
20.已知函数f(x)=ex和函数g(x)=kx+m(k、m为实数,e为自然对数的底数,e≈2.71828).
(1)求函数h(x)=f(x)﹣g(x)的单调区间;
(2)当k=2,m=1时,判断方程f(x)=g(x)的实数根的个数并证明;
(3)已知m≠1,不等式(m﹣1)[f(x)﹣g(x)]≤0对任意实数x恒成立,求km的最大值.
【考点】6E:利用导数求闭区间上函数的最值;6B:利用导数研究函数的单调性.
【分析】(1)求出h′(x)=ex﹣k,(x∈R),分以下两种情况讨论:①当k≤0,②当k>0,
(2)当k=2,m=1时,方程f(x)=g(x)即为h(x)=ex﹣2x﹣1=0,结合(1)及图象即可判定.
(3)设h(x)=f(x)﹣g(x),分①当m>1,②当m<1,分别求解
【解答】解:(1)h′(x)=ex﹣k,(x∈R),
①当k≤0时,h′(x)>0恒成立,h(x)的单调递增区间为(﹣∞,+∞),无单调递减区间;
②当k>0时,由h′(x)>0得x>lnk,由h′(x)<0得x<lnk,
故h(x)的单调递减区间为(﹣∞,lnk),单调递增区间为(lnk,+∞).
(2)当k=2,m=1时,方程f(x)=g(x)即为h(x)=ex﹣2x﹣1=0,
由(1)知h(x)在(﹣∞,ln2)上递减,而h(0)=0,故h(x)在(﹣∞,ln2)上有且仅有1个零点,
由(1)知h(x)在[ln2,+∞)上递增,而h(1)=e﹣3<0,h(2)=e2﹣5>0,且h(x)的图象在[1,2]上是连续不间断的,
故h(x)在[1,2]上有且仅有1个零点,所以h(x)在[ln2,+∞)上也有且仅有1个零点,
综上,方程f(x)=g(x)有且仅有两个实数根.
(3)设h(x)=f(x)﹣g(x),
①当m>1时,f(x)﹣g(x)≤0恒成立,则h(x)≤0恒成立,
而h(﹣)=e>0,与h(x)≤0恒成立矛盾,故m>1不合题意;
②当m<1时,f(x)﹣g(x)≥0,恒成立,则h(x)≥0恒成立,
1°当k=0时,由h(x)=ex﹣m≥0恒成立可得m∈(﹣∞,0],km=0;
2°当k<0时,h()=e﹣1,而,故e<1,
故h()<0,与h(x)≥0恒成立矛盾,故k<0不合题意;
3°当k>0时,由(1)可知[h(x)]min=h(lnk)=k﹣klnk﹣m,而h(x)≥0恒成立,
故k﹣klnk﹣m≥0,得m≤k﹣klnk,故km≤k(k﹣klnk),
记φ(k)=k(k﹣klnk),(k>0),
则φ′(k)=k(1﹣2lnk),由φ′(k)>0得0,由φ′(k)<0得k>,
故φ(k)在(0,)上单调递增,在(,+∞)上单调递减,
∴φ(k)max=φ()=,∴km≤,当且仅当k=,m=时取等号;
综上①②两种情况得km的最大值为.
同课章节目录
