13.1三角形中的边角关系同步练习(解析版)
文档属性
| 名称 | 13.1三角形中的边角关系同步练习(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 90.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-08-29 00:00:00 | ||
图片预览



文档简介
沪科版八年级数学上册同步练习
13.1三角形中的边角关系
一、单选题
1、如果一个三角形的两边长分别为2和4,则第三边长可能是(?? )
A、2 B、4 C、6 D、8
2、下列长度的三条线段能组成三角形的是(?? )
A、3,4,8 B、5,6,11 C、5,6,10 D、1,2,3
3、下列能判定三角形是等腰三角形的是(?? )
A、有两个角为30°、60° B、有两个角为40°、80° C、有两个角为50°、80° D、有两个角为100°、120°
4、已知△ABC的外角∠CBE,∠BCF的角平分线BP,CP交于P点,则∠BPC是(? )
A、钝角 B、锐角 C、直角 D、无法确定
5、如图:∠2 大于∠1的是(? )
A、 B、 C、D、
6、下列说法中不正确的是(? )
A、三角形按边分可分为不等边三角形、等腰三角形 B、等腰三角形的内角可能是钝角或直角 C、三角形外角一定是钝角 D、三角形的中线把三角形分成面积相等的两部分【来源:21·世纪·教育·网】
7、如图,已知D为BC上一点,∠B=∠1,∠BAC=78°,则∠2=(? )
A、78° B、80° C、50° D、60°
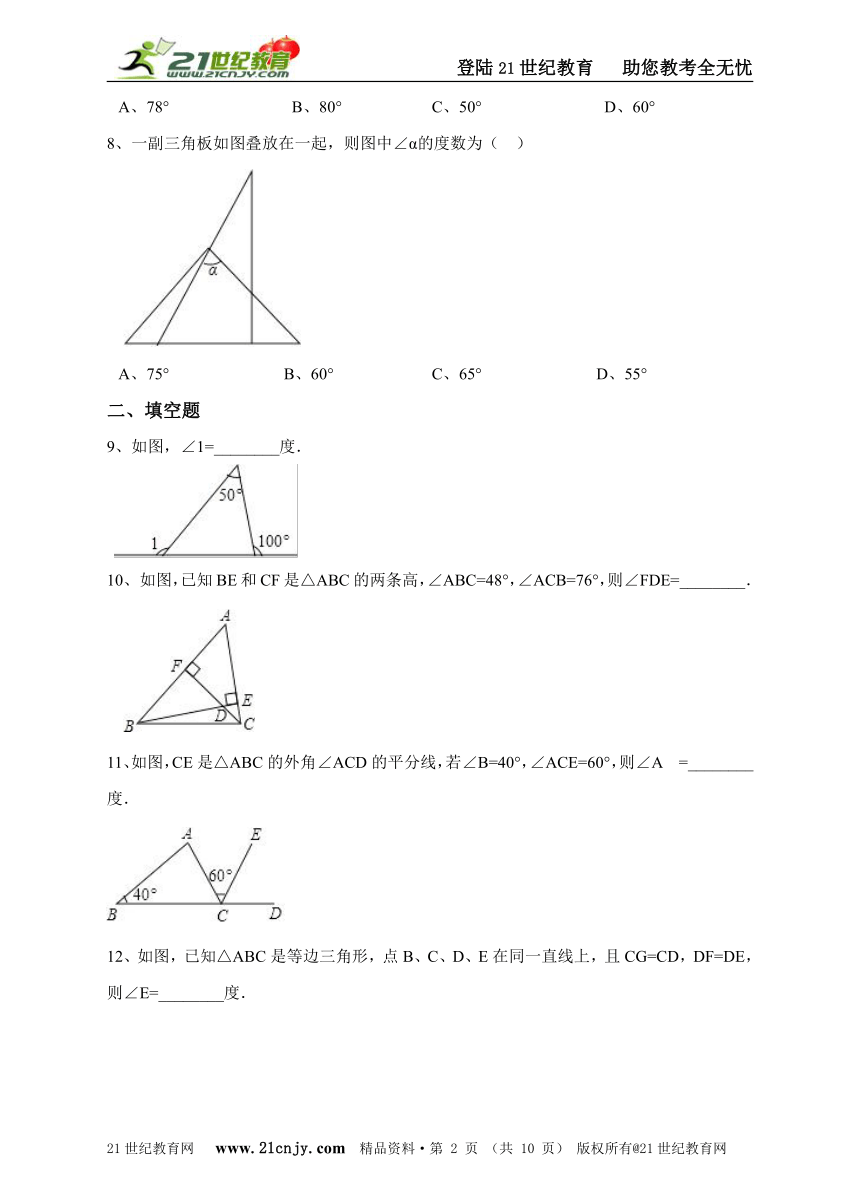
一副三角板如图叠放在一起,则图中∠α的度数为(?? )
A、75° B、60° C、65° D、55°
二、填空题
9、如图,∠1=________度.
如图,已知BE和CF是△ABC的两条高,∠ABC=48°,∠ACB=76°,则∠FDE=________.
11、如图,CE是△ABC的外角∠ACD的平分线,若∠B=40°,∠ACE=60°,则∠A =________度. www.21-cn-jy.com
12、如图,已知△ABC是等边三角形,点B、C、D、E在同一直线上,且CG=CD,DF=DE,则∠E=________度. 2-1-c-n-j-y
13、一个三角形的三个外角之比为5:4:3,则这个三角形内角中最大的角是________度.
14、补全解题过程.
如图,在△ABC中∠ABC平分线BP和外角平分线CP交于点P,试猜想∠A与∠P之间的关系,并说明理由. 解:∠A=2∠P 理由:∵BP、CP分别平分∠ABC、∠ACD(已知) ∴∠ABC=________∠1,∠ACD=2∠2 (________) ∵∠ACD为△ABC的外角 ∴∠ACD=∠A+∠________=∠A+2∠1(三角形外角的性质) 即:2∠2=∠A+2∠1 同理:∠2=∠P+________ ∴∠A=2∠P. 2·1·c·n·j·y
三、解答题
15、附加题:如图,已知∠1=∠2,∠3=∠4,∠A=100°,求x的值.
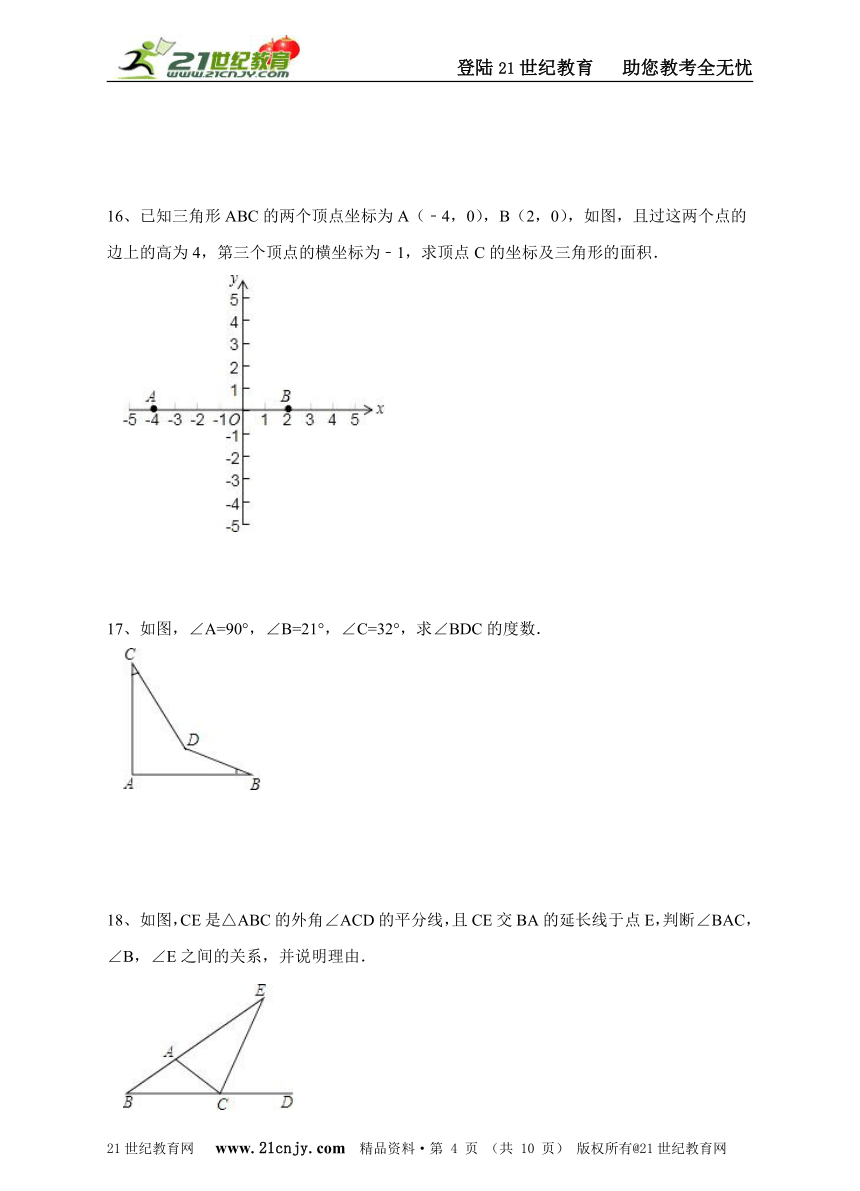
已知三角形ABC的两个顶点坐标为A(﹣4,0),B(2,0),如图,且过这两个点的边上的高为4,第三个顶点的横坐标为﹣1,求顶点C的坐标及三角形的面积.
如图,∠A=90°,∠B=21°,∠C=32°,求∠BDC的度数.
如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,判断∠BAC,∠B,∠E之间的关系,并说明理由.21教育网
参考答案与解析
一、单选题
1、B 解:设第三边长为x,则由三角形三边关系定理得4﹣2<x<4+2,即2<x<6. 因此,本题的第三边应满足2<x<6,把各项代入不等式符合的即为答案. 2,6,8都不符合不等式2<x<6,只有4符合不等式. 故选B. 21·cn·jy·com
2、C 解:3+4<8,则3,4,8不能组成三角形,A不符合题意; 5+6=11,则5,6,11不能组成三角形,B不合题意;
3、 C 解:A,因为有两个角为30°、60°,则第三个角为90°,所以此选项不正确; B,因为有两个角为40°、80°,则第三个角为60°,所以此选项不正确; C,因为有两个角为50°、80°,则第三个角为50°,有两个角相等,所以此选项正确; D,因为100°+120°>180°,所以此选项不正确; 故选C. 4、 B 解:21cnjy.com
∵△ABC的外角平分线BP,CP交于P点, ∴∠PBC= ∠EBC,∠BCP= ∠BCF, ∵∠CBE、∠BCF是△ABC的两个外角, ∴∠CBE+∠BCF=360°﹣(180°﹣∠A)=180°+∠A, ∴∠PBC+∠BCP= (∠EBC+∠BCF)= (180°+∠A)=90°+ ∠A, ∵在△PBC中,∠BPC=180°﹣(∠PBC+∠BCP)=180°﹣(90°+ ∠A)=90°﹣ ∠A<90°, ∴∠BPC是锐角. 故选:B. 5、 B 解:A、∠2 和∠1的关系不能确定,故错误; B、∠2>∠1,故正确; C、∠2 和∠1的关系不能确定,故错误; D、∠2=∠1,故错误, 故选:B. 6、 C 解:三角形按边分可分为不等边三角形、等腰三角形,故A不正确;
B、等腰三角形的内角可能是钝角或直角,故B不正确; C、三角形外角可能是钝角、直角或锐角,故C正确; D、三角形的中线把三角形分成面积相等的两部分,故D不正确; 故选C、 7、 A 解:∵∠2=∠B+∠BAD,∠BAC=∠1+∠BAD, 又∵∠B=∠1, ∴∠2=∠BAC, ∵∠BAC=78°, ∴∠2=78°. 故选A.www-2-1-cnjy-com
8、A 解:如图,∵∠1=60°,∠2=45°, ∴∠α=180°﹣45°﹣60°=75°, 故选A. 21*cnjy*com
二、填空题
9、130 解:如图,∠2=180°﹣100°=80°, 则∠1=50°+∠2=130°. 故答案是:130. 【来源:21cnj*y.co*m】
10、124° 解:(法一)在△ABC中, ∵∠A+∠ABC+∠ACB=180° ∴∠A=180°﹣48°﹣76°=56° 在四边形AFDE中, ∵∠A+∠AFC+∠AEB+∠FDE=360° 又∵∠AFC=∠AEB=90°,∠A=56° ∴∠FDE=360°﹣90°﹣90°﹣56° =124° 故答案为:124° (法二)∵∠AEB=∠ACB+∠EBC=90°,∠AFC=∠ABC+∠FCB=90°, ∴∠CBE=14°,∠FCB=42°, ∵∠BDC=180°﹣∠CBE﹣∠FCB=124°, ∴∠FDE=124°. 故答案为:124°21世纪教育网版权所有
11、80 解:∵∠ACE=60°,CE是△ABC的外角∠ACD的平分线, ∠ACD=2∠ACE=120°, ∵∠ACD=∠A+∠B,∠B=40°, ∴∠A=∠ACD﹣∠B=80°, 故答案为:80 12、15 解:∵△ABC是等边三角形, ∴∠ACB=60°,∠ACD=120°, ∵CG=CD, ∴∠CDG=30°,∠FDE=150°, ∵DF=DE, ∴∠E=15°. 故答案为:15. 【版权所有:21教育】
13、 90 解:∵一个三角形的三个外角之比为3:4:5, ∴设角形的三个外角分别为3x,4x,5x,则3x+4x+5x=360°, 解得x=30°, ∴3x=90°,4x=120°,5x=150°, ∴与之对应的内角分别为:90°,60°,30°, ∴三角形内角中最大的角是90°, 故答案为:9021教育名师原创作品
14、2;角平分线的定义;ABC;∠1 解:∠A=2∠P 理由:∵BP、CP分别平分∠ABC、∠ACD(已知) ∴∠ABC=2∠1,∠ACD=2∠2 (角平分线的定义) ∵∠ACD为△ABC的外角 ∴∠ACD=∠A+∠ABC=∠A+2∠1(三角形外角的性质) 即:2∠2=∠A+2∠1, 同理:∠2=∠P+∠1, ∴∠A=2∠P. 故答案为:2,角平分线的定义,ABC,∠1. 21*cnjy*com
三、解答题
15、解:∵在△ABC中,∠A+∠ABC+∠ACB=180°,∠A=100°, ∴∠ABC+∠ACB=180°﹣100°=80°, ∵∠1=∠2,∠3=∠4, ∴∠2+∠4=(∠ABC+∠ACB)=40°, ∴x=180°﹣(∠2+∠4)=140°. 21·世纪*教育网
16、解:∵AB边上的高为4, ∴点C的纵坐标为4或﹣4, ∵第三个顶点C的横坐标为﹣1, ∴点C的坐标为(﹣1,4)或(﹣1,﹣4); ∵A(﹣4,0),B(2,0), ∴AB=2﹣(﹣4)=2+4=6, ∴△ABC的面积= ×6×4=12.
17、解:如图,连接AD并延长AD至点E,
∵∠BDE=∠BAE+∠B,∠CDE=∠CAD+∠C ∴∠BDC=∠BDE+∠CDE=∠CAD+∠C+∠BAD+∠B=∠BAC+∠B+∠C ∵∠A=90°,∠B=21°,∠C=32°, ∴∠BDC=90°+21°+32°=143°. 【出处:21教育名师】
18、解:∠BAC=∠B+2∠E. 理由:在△BCE中,∠DCE=∠B+∠E, 因为CE是△ABC的外角∠ACD的平分线, 所以∠DCE=∠ACE. 在△ACE中,∠BAC=∠E+∠ACE=∠E+∠B+∠E=∠B+2∠E, 即∠BAC=∠B+2∠E.
13.1三角形中的边角关系
一、单选题
1、如果一个三角形的两边长分别为2和4,则第三边长可能是(?? )
A、2 B、4 C、6 D、8
2、下列长度的三条线段能组成三角形的是(?? )
A、3,4,8 B、5,6,11 C、5,6,10 D、1,2,3
3、下列能判定三角形是等腰三角形的是(?? )
A、有两个角为30°、60° B、有两个角为40°、80° C、有两个角为50°、80° D、有两个角为100°、120°
4、已知△ABC的外角∠CBE,∠BCF的角平分线BP,CP交于P点,则∠BPC是(? )
A、钝角 B、锐角 C、直角 D、无法确定
5、如图:∠2 大于∠1的是(? )
A、 B、 C、D、
6、下列说法中不正确的是(? )
A、三角形按边分可分为不等边三角形、等腰三角形 B、等腰三角形的内角可能是钝角或直角 C、三角形外角一定是钝角 D、三角形的中线把三角形分成面积相等的两部分【来源:21·世纪·教育·网】
7、如图,已知D为BC上一点,∠B=∠1,∠BAC=78°,则∠2=(? )
A、78° B、80° C、50° D、60°
一副三角板如图叠放在一起,则图中∠α的度数为(?? )
A、75° B、60° C、65° D、55°
二、填空题
9、如图,∠1=________度.
如图,已知BE和CF是△ABC的两条高,∠ABC=48°,∠ACB=76°,则∠FDE=________.
11、如图,CE是△ABC的外角∠ACD的平分线,若∠B=40°,∠ACE=60°,则∠A =________度. www.21-cn-jy.com
12、如图,已知△ABC是等边三角形,点B、C、D、E在同一直线上,且CG=CD,DF=DE,则∠E=________度. 2-1-c-n-j-y
13、一个三角形的三个外角之比为5:4:3,则这个三角形内角中最大的角是________度.
14、补全解题过程.
如图,在△ABC中∠ABC平分线BP和外角平分线CP交于点P,试猜想∠A与∠P之间的关系,并说明理由. 解:∠A=2∠P 理由:∵BP、CP分别平分∠ABC、∠ACD(已知) ∴∠ABC=________∠1,∠ACD=2∠2 (________) ∵∠ACD为△ABC的外角 ∴∠ACD=∠A+∠________=∠A+2∠1(三角形外角的性质) 即:2∠2=∠A+2∠1 同理:∠2=∠P+________ ∴∠A=2∠P. 2·1·c·n·j·y
三、解答题
15、附加题:如图,已知∠1=∠2,∠3=∠4,∠A=100°,求x的值.
已知三角形ABC的两个顶点坐标为A(﹣4,0),B(2,0),如图,且过这两个点的边上的高为4,第三个顶点的横坐标为﹣1,求顶点C的坐标及三角形的面积.
如图,∠A=90°,∠B=21°,∠C=32°,求∠BDC的度数.
如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,判断∠BAC,∠B,∠E之间的关系,并说明理由.21教育网
参考答案与解析
一、单选题
1、B 解:设第三边长为x,则由三角形三边关系定理得4﹣2<x<4+2,即2<x<6. 因此,本题的第三边应满足2<x<6,把各项代入不等式符合的即为答案. 2,6,8都不符合不等式2<x<6,只有4符合不等式. 故选B. 21·cn·jy·com
2、C 解:3+4<8,则3,4,8不能组成三角形,A不符合题意; 5+6=11,则5,6,11不能组成三角形,B不合题意;
3、 C 解:A,因为有两个角为30°、60°,则第三个角为90°,所以此选项不正确; B,因为有两个角为40°、80°,则第三个角为60°,所以此选项不正确; C,因为有两个角为50°、80°,则第三个角为50°,有两个角相等,所以此选项正确; D,因为100°+120°>180°,所以此选项不正确; 故选C. 4、 B 解:21cnjy.com
∵△ABC的外角平分线BP,CP交于P点, ∴∠PBC= ∠EBC,∠BCP= ∠BCF, ∵∠CBE、∠BCF是△ABC的两个外角, ∴∠CBE+∠BCF=360°﹣(180°﹣∠A)=180°+∠A, ∴∠PBC+∠BCP= (∠EBC+∠BCF)= (180°+∠A)=90°+ ∠A, ∵在△PBC中,∠BPC=180°﹣(∠PBC+∠BCP)=180°﹣(90°+ ∠A)=90°﹣ ∠A<90°, ∴∠BPC是锐角. 故选:B. 5、 B 解:A、∠2 和∠1的关系不能确定,故错误; B、∠2>∠1,故正确; C、∠2 和∠1的关系不能确定,故错误; D、∠2=∠1,故错误, 故选:B. 6、 C 解:三角形按边分可分为不等边三角形、等腰三角形,故A不正确;
B、等腰三角形的内角可能是钝角或直角,故B不正确; C、三角形外角可能是钝角、直角或锐角,故C正确; D、三角形的中线把三角形分成面积相等的两部分,故D不正确; 故选C、 7、 A 解:∵∠2=∠B+∠BAD,∠BAC=∠1+∠BAD, 又∵∠B=∠1, ∴∠2=∠BAC, ∵∠BAC=78°, ∴∠2=78°. 故选A.www-2-1-cnjy-com
8、A 解:如图,∵∠1=60°,∠2=45°, ∴∠α=180°﹣45°﹣60°=75°, 故选A. 21*cnjy*com
二、填空题
9、130 解:如图,∠2=180°﹣100°=80°, 则∠1=50°+∠2=130°. 故答案是:130. 【来源:21cnj*y.co*m】
10、124° 解:(法一)在△ABC中, ∵∠A+∠ABC+∠ACB=180° ∴∠A=180°﹣48°﹣76°=56° 在四边形AFDE中, ∵∠A+∠AFC+∠AEB+∠FDE=360° 又∵∠AFC=∠AEB=90°,∠A=56° ∴∠FDE=360°﹣90°﹣90°﹣56° =124° 故答案为:124° (法二)∵∠AEB=∠ACB+∠EBC=90°,∠AFC=∠ABC+∠FCB=90°, ∴∠CBE=14°,∠FCB=42°, ∵∠BDC=180°﹣∠CBE﹣∠FCB=124°, ∴∠FDE=124°. 故答案为:124°21世纪教育网版权所有
11、80 解:∵∠ACE=60°,CE是△ABC的外角∠ACD的平分线, ∠ACD=2∠ACE=120°, ∵∠ACD=∠A+∠B,∠B=40°, ∴∠A=∠ACD﹣∠B=80°, 故答案为:80 12、15 解:∵△ABC是等边三角形, ∴∠ACB=60°,∠ACD=120°, ∵CG=CD, ∴∠CDG=30°,∠FDE=150°, ∵DF=DE, ∴∠E=15°. 故答案为:15. 【版权所有:21教育】
13、 90 解:∵一个三角形的三个外角之比为3:4:5, ∴设角形的三个外角分别为3x,4x,5x,则3x+4x+5x=360°, 解得x=30°, ∴3x=90°,4x=120°,5x=150°, ∴与之对应的内角分别为:90°,60°,30°, ∴三角形内角中最大的角是90°, 故答案为:9021教育名师原创作品
14、2;角平分线的定义;ABC;∠1 解:∠A=2∠P 理由:∵BP、CP分别平分∠ABC、∠ACD(已知) ∴∠ABC=2∠1,∠ACD=2∠2 (角平分线的定义) ∵∠ACD为△ABC的外角 ∴∠ACD=∠A+∠ABC=∠A+2∠1(三角形外角的性质) 即:2∠2=∠A+2∠1, 同理:∠2=∠P+∠1, ∴∠A=2∠P. 故答案为:2,角平分线的定义,ABC,∠1. 21*cnjy*com
三、解答题
15、解:∵在△ABC中,∠A+∠ABC+∠ACB=180°,∠A=100°, ∴∠ABC+∠ACB=180°﹣100°=80°, ∵∠1=∠2,∠3=∠4, ∴∠2+∠4=(∠ABC+∠ACB)=40°, ∴x=180°﹣(∠2+∠4)=140°. 21·世纪*教育网
16、解:∵AB边上的高为4, ∴点C的纵坐标为4或﹣4, ∵第三个顶点C的横坐标为﹣1, ∴点C的坐标为(﹣1,4)或(﹣1,﹣4); ∵A(﹣4,0),B(2,0), ∴AB=2﹣(﹣4)=2+4=6, ∴△ABC的面积= ×6×4=12.
17、解:如图,连接AD并延长AD至点E,
∵∠BDE=∠BAE+∠B,∠CDE=∠CAD+∠C ∴∠BDC=∠BDE+∠CDE=∠CAD+∠C+∠BAD+∠B=∠BAC+∠B+∠C ∵∠A=90°,∠B=21°,∠C=32°, ∴∠BDC=90°+21°+32°=143°. 【出处:21教育名师】
18、解:∠BAC=∠B+2∠E. 理由:在△BCE中,∠DCE=∠B+∠E, 因为CE是△ABC的外角∠ACD的平分线, 所以∠DCE=∠ACE. 在△ACE中,∠BAC=∠E+∠ACE=∠E+∠B+∠E=∠B+2∠E, 即∠BAC=∠B+2∠E.
