2017年秋人教版九年级上册数学22.1.1 二次函数课件
文档属性
| 名称 | 2017年秋人教版九年级上册数学22.1.1 二次函数课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 163.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-08-31 00:00:00 | ||
图片预览








文档简介
课件21张PPT。第二十二章 二次函数
22.1 二次函数的图象和性质
22.1.1 二次函数
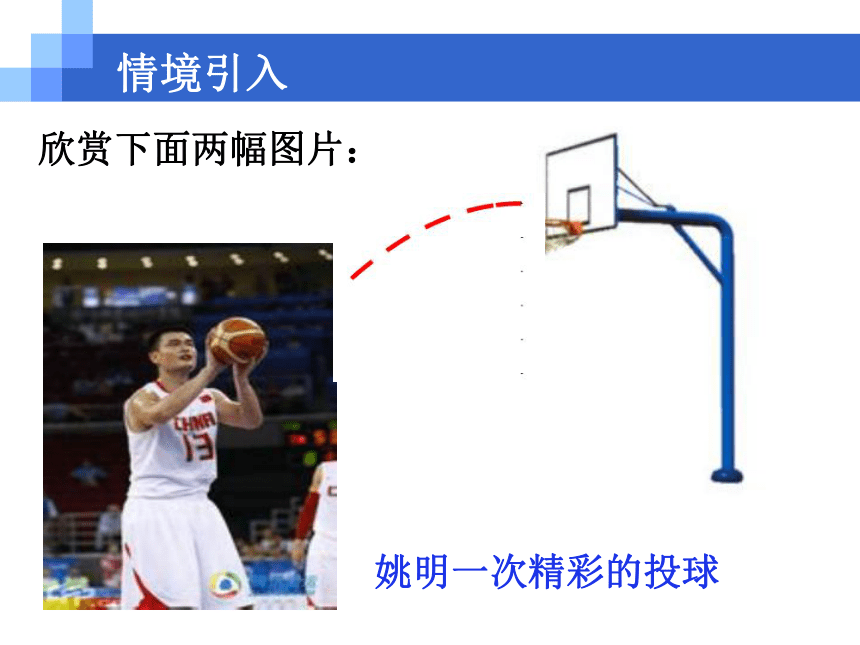
情境引入姚明一次精彩的投球欣赏下面两幅图片:情境引入广场前喷水池喷出的水珠情境引入 篮球和水珠在空中走过一条曲线,在曲线的各个位置上,篮球(水珠)的竖直高度h与它距离投出位置(喷头)的水平距离x之间有什么关系?上面问题中变量之间的关系可以用二次函数来表示.自主探究1.问题探究
(1)正方体的六个面是全等的正方形,如果正方体的棱长为x,表面积为y,那么y与x的关系可以怎样表示?
(2) n边形的对角线条数d与边数n之间有怎样的关系?
(3)某工厂一种产品现在的年产量是20件,计划今后两年增加产量,如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而定,y与x之间的关系应怎样表示?自主探究自主探究2.观察思考
请观察下面三个式子,它们的变量对应规律可用怎样的函数表示?这些函数有什么共同特点?请你结合学习一次函数概念的经验,给它下个定义.
(1)
(2)
(3)具有y=ax2+bx+c(a≠0)的形式自主探究3.归纳总结 一般地,形如 (a,b,c是常数,a≠0)的函数,叫做二次函数,其中x是自变量,a,b,c分别是二次项系数、一次项系数和常数项.二次函数的定义:自主探究问题:
(1)二次函数概念中a,b,c有怎样的要求?
a,b,c是常数,a≠0.自主探究(2)当a=0时,这个函数还是二次函数吗?为什么?
当a=0时,这个函数不是二次函数,有可能是一次函数.问题:自主探究问题:
(3)b或c能为0吗?
当b≠0时,是一次函数,
当b=0时, 是常数函数.
c 可以为0.典例探究例(补充):关于x的函数 是二次函数,求m的值.
解:由题意可得
解得 m = 2.
∴m=2时,函数为二次函数.典例探究巩固练习1.教材第29页练习第1,2题.(1)一个圆柱的高等于底面的半径,写出它的表面积S
与底面半径r之间的关系.(2)如图,矩形绿地的长、宽各增加x m,写出扩充后的绿地的面积y与x的关系式.巩固练习
2. 若函数 为二次函数, 求m的值.答案:m = 2.巩固练习3. 下列函数中,哪些是二次函数?答案: 二次函数有:② ④.巩固练习 4.你能举出一些生活中的二次函数的例子吗?总结提高 1. 通过本节课的学习,你有哪些收获?还有什么疑惑?说给老师或同学听听.
总结提高 2.二次函数的一般形式是什么样?特殊形式有哪些?一个函数是不是二次函数,关键看什么?当a =0时,这个函数不是二次函数,有可能是一次函数.布置作业必做题:
教材第41页习题22.1第1,2题.
选做题:
教材第56页复习题22第1,2题.谢谢 !
22.1 二次函数的图象和性质
22.1.1 二次函数
情境引入姚明一次精彩的投球欣赏下面两幅图片:情境引入广场前喷水池喷出的水珠情境引入 篮球和水珠在空中走过一条曲线,在曲线的各个位置上,篮球(水珠)的竖直高度h与它距离投出位置(喷头)的水平距离x之间有什么关系?上面问题中变量之间的关系可以用二次函数来表示.自主探究1.问题探究
(1)正方体的六个面是全等的正方形,如果正方体的棱长为x,表面积为y,那么y与x的关系可以怎样表示?
(2) n边形的对角线条数d与边数n之间有怎样的关系?
(3)某工厂一种产品现在的年产量是20件,计划今后两年增加产量,如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而定,y与x之间的关系应怎样表示?自主探究自主探究2.观察思考
请观察下面三个式子,它们的变量对应规律可用怎样的函数表示?这些函数有什么共同特点?请你结合学习一次函数概念的经验,给它下个定义.
(1)
(2)
(3)具有y=ax2+bx+c(a≠0)的形式自主探究3.归纳总结 一般地,形如 (a,b,c是常数,a≠0)的函数,叫做二次函数,其中x是自变量,a,b,c分别是二次项系数、一次项系数和常数项.二次函数的定义:自主探究问题:
(1)二次函数概念中a,b,c有怎样的要求?
a,b,c是常数,a≠0.自主探究(2)当a=0时,这个函数还是二次函数吗?为什么?
当a=0时,这个函数不是二次函数,有可能是一次函数.问题:自主探究问题:
(3)b或c能为0吗?
当b≠0时,是一次函数,
当b=0时, 是常数函数.
c 可以为0.典例探究例(补充):关于x的函数 是二次函数,求m的值.
解:由题意可得
解得 m = 2.
∴m=2时,函数为二次函数.典例探究巩固练习1.教材第29页练习第1,2题.(1)一个圆柱的高等于底面的半径,写出它的表面积S
与底面半径r之间的关系.(2)如图,矩形绿地的长、宽各增加x m,写出扩充后的绿地的面积y与x的关系式.巩固练习
2. 若函数 为二次函数, 求m的值.答案:m = 2.巩固练习3. 下列函数中,哪些是二次函数?答案: 二次函数有:② ④.巩固练习 4.你能举出一些生活中的二次函数的例子吗?总结提高 1. 通过本节课的学习,你有哪些收获?还有什么疑惑?说给老师或同学听听.
总结提高 2.二次函数的一般形式是什么样?特殊形式有哪些?一个函数是不是二次函数,关键看什么?当a =0时,这个函数不是二次函数,有可能是一次函数.布置作业必做题:
教材第41页习题22.1第1,2题.
选做题:
教材第56页复习题22第1,2题.谢谢 !
同课章节目录
