2017年秋人教版九年级上册数学 22.1.2 二次函数 y=ax2的图象和性质课件
文档属性
| 名称 | 2017年秋人教版九年级上册数学 22.1.2 二次函数 y=ax2的图象和性质课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 192.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-08-31 00:00:00 | ||
图片预览







文档简介
课件22张PPT。第二十二章 二次函数
22.1 二次函数的图象和性质
22.1.2 二次函数 y=ax2的图象和性质
情境引入 1. 二次函数的一般形式是什么?(a,b,c是常数,a≠0)对各项系数有何要求?情境引入 2.通过一次函数的学习我们知道,要研究函数性质的出发点是什么?它需要哪些步骤?画图
步骤是:列表、描点、连线.情境引入4.请你画出二次函数 的图象.
3.你认为最简单的二次函数形式是什么?体验画图1.列表:
(1)二次函数 的自变量取值范围是什么?一切实数 你能取完自变量x的所有值吗?如果不能,你认为在列出的表格中自变量x取哪些值合适?可对称取值
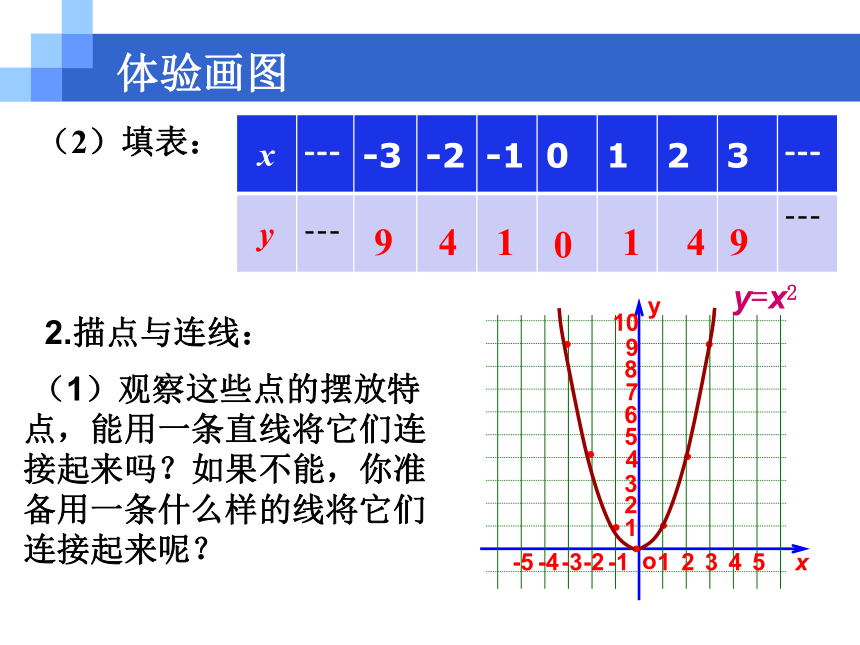
(负数、零、正数)体验画图(2)填表:
9410149y=x22.描点与连线:
(1)观察这些点的摆放特点,能用一条直线将它们连接起来吗?如果不能,你准备用一条什么样的线将它们连接起来呢?
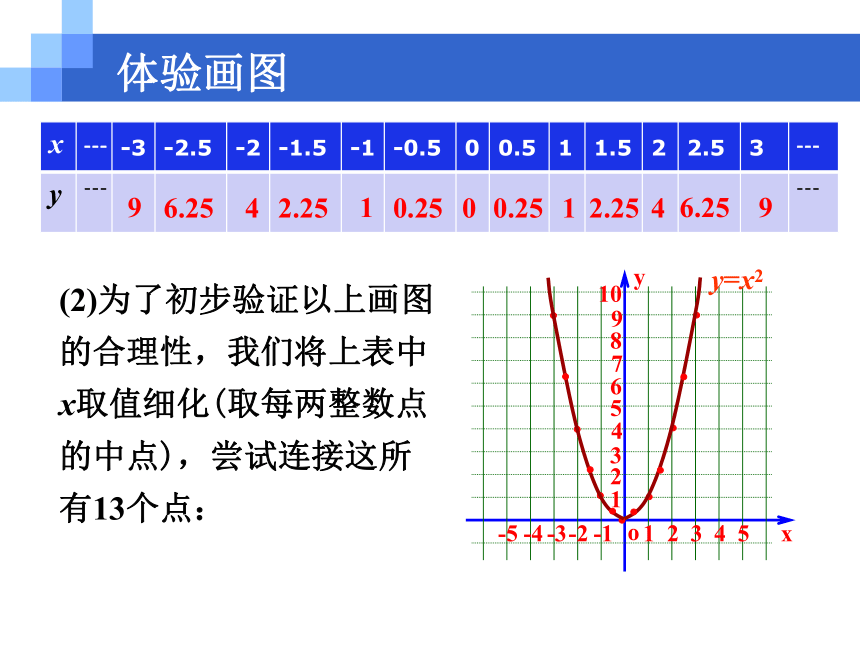
(2)为了初步验证以上画图的合理性,我们将上表中x取值细化(取每两整数点的中点),尝试连接这所有13个点:
体验画图96.2542.2510.2500.2512.2546.259y=x2(3)为了更精确验证这个函数图象,可以运用计算机辅助,取每两个整数点的三等分点,乃至100等分点,并将这些点连接起来.
体验画图 它类似于投篮和投掷铅球时,球在空中所经过的路线,只是这条曲线叫做抛物线.
实际上,二次函数的图象是抛物线,它们开口向上或向下,一般地,二次函数 的图象叫做抛物线 .体验画图抛物线的定义:体验画图3. 拓展与延伸:
(1)画二次函数的图象一般需要___个点,
哪些点比较关键?3轴 抛物线 是__对称图形,对称
轴是 y 轴.体验画图(2)依据以上经验,要在同一直角坐标系画出二次函数 和 的图象有何技巧?试画出图象;比较它们与抛物线 有何共同点和不同点?a>0 共同点是:
都开口向上,顶点都在原点.不同点是:
开口大小不同.体验画图a<0 总结性质1.形如二次函数 y=ax2 的图象都是顶点为______的抛物线,反之,顶点在(0,0)的抛物线的形式是_________. (0,0)y = ax2总结性质向上
向下
关于y轴对称原点(0,0)
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
2.填表:最小值是0
最大值是0总结性质3. |a|越大,开口越_____;|a|越小,开口越_____.
小大4. 比较函数 y = x2 和y = - x2 的图象,有何区别和联系?
的图象呢?
y = 2x2 和 y = - 2x2 的图象呢?每一组的开口大小都相同,方向都相反.总结性质5. 请你从解析式的角度解释为什么 y = ax2 的图象对称轴都是y轴呢?为什么顶点都是原点?最值为什么都是0? 当x=0时,y=0.基础练习(一)教材第32页练习说出下列抛物线的开口方向、对称轴和顶点:基础练习补充练习: 1.函数y=2x2的图象的开口 ,对称轴是 ,顶点是 . 2.函数y=-3x2的图象的开口 ,对称轴是 ,顶点是 .向上向下y 轴y 轴(0,0)(0,0)精讲例题 例 将抛物线 y = ax2 绕顶点旋转180°后经过点(-1,2),试求常数 a 的值.分析:抛物线 y = ax2 绕顶点旋转180°后,抛物线的解析式为y = - ax2,将点(-1,2)的坐标代入这个解析式即可求出 a 的值.答案:-2总结提高1. 形如 y = ax2 的图象有何共同特点?a的绝对值越大,开口越小
关于 y 轴对称 原点(0,0)
总结提高 2. 二次项系数 a 对形如 y=ax2 的函数值 y 又有
何影响?对图象又有何影响?开口向上
开口向下
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
谢谢 !
22.1 二次函数的图象和性质
22.1.2 二次函数 y=ax2的图象和性质
情境引入 1. 二次函数的一般形式是什么?(a,b,c是常数,a≠0)对各项系数有何要求?情境引入 2.通过一次函数的学习我们知道,要研究函数性质的出发点是什么?它需要哪些步骤?画图
步骤是:列表、描点、连线.情境引入4.请你画出二次函数 的图象.
3.你认为最简单的二次函数形式是什么?体验画图1.列表:
(1)二次函数 的自变量取值范围是什么?一切实数 你能取完自变量x的所有值吗?如果不能,你认为在列出的表格中自变量x取哪些值合适?可对称取值
(负数、零、正数)体验画图(2)填表:
9410149y=x22.描点与连线:
(1)观察这些点的摆放特点,能用一条直线将它们连接起来吗?如果不能,你准备用一条什么样的线将它们连接起来呢?
(2)为了初步验证以上画图的合理性,我们将上表中x取值细化(取每两整数点的中点),尝试连接这所有13个点:
体验画图96.2542.2510.2500.2512.2546.259y=x2(3)为了更精确验证这个函数图象,可以运用计算机辅助,取每两个整数点的三等分点,乃至100等分点,并将这些点连接起来.
体验画图 它类似于投篮和投掷铅球时,球在空中所经过的路线,只是这条曲线叫做抛物线.
实际上,二次函数的图象是抛物线,它们开口向上或向下,一般地,二次函数 的图象叫做抛物线 .体验画图抛物线的定义:体验画图3. 拓展与延伸:
(1)画二次函数的图象一般需要___个点,
哪些点比较关键?3轴 抛物线 是__对称图形,对称
轴是 y 轴.体验画图(2)依据以上经验,要在同一直角坐标系画出二次函数 和 的图象有何技巧?试画出图象;比较它们与抛物线 有何共同点和不同点?a>0 共同点是:
都开口向上,顶点都在原点.不同点是:
开口大小不同.体验画图a<0 总结性质1.形如二次函数 y=ax2 的图象都是顶点为______的抛物线,反之,顶点在(0,0)的抛物线的形式是_________. (0,0)y = ax2总结性质向上
向下
关于y轴对称原点(0,0)
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
2.填表:最小值是0
最大值是0总结性质3. |a|越大,开口越_____;|a|越小,开口越_____.
小大4. 比较函数 y = x2 和y = - x2 的图象,有何区别和联系?
的图象呢?
y = 2x2 和 y = - 2x2 的图象呢?每一组的开口大小都相同,方向都相反.总结性质5. 请你从解析式的角度解释为什么 y = ax2 的图象对称轴都是y轴呢?为什么顶点都是原点?最值为什么都是0? 当x=0时,y=0.基础练习(一)教材第32页练习说出下列抛物线的开口方向、对称轴和顶点:基础练习补充练习: 1.函数y=2x2的图象的开口 ,对称轴是 ,顶点是 . 2.函数y=-3x2的图象的开口 ,对称轴是 ,顶点是 .向上向下y 轴y 轴(0,0)(0,0)精讲例题 例 将抛物线 y = ax2 绕顶点旋转180°后经过点(-1,2),试求常数 a 的值.分析:抛物线 y = ax2 绕顶点旋转180°后,抛物线的解析式为y = - ax2,将点(-1,2)的坐标代入这个解析式即可求出 a 的值.答案:-2总结提高1. 形如 y = ax2 的图象有何共同特点?a的绝对值越大,开口越小
关于 y 轴对称 原点(0,0)
总结提高 2. 二次项系数 a 对形如 y=ax2 的函数值 y 又有
何影响?对图象又有何影响?开口向上
开口向下
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
谢谢 !
同课章节目录
