2017年秋人教版九年级上册数学 22.1.3二次函数y=a(x-h)2的图象和性质课件
文档属性
| 名称 | 2017年秋人教版九年级上册数学 22.1.3二次函数y=a(x-h)2的图象和性质课件 |  | |
| 格式 | zip | ||
| 文件大小 | 280.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-08-31 22:47:03 | ||
图片预览







文档简介
课件26张PPT。第二十二章 二次函数
22.1 二次函数的图象和性质
22.1.3 二次函数 y=a(x-h)2+k的图象和性质
第2课时 二次函数 y=a(x-h)2的图象和性质情境引入抛物线之间的平移规律:抛物线 y=ax2抛物线 y=ax2-k向上平移
k(k>0)个单位抛物线 y=ax2向下平移
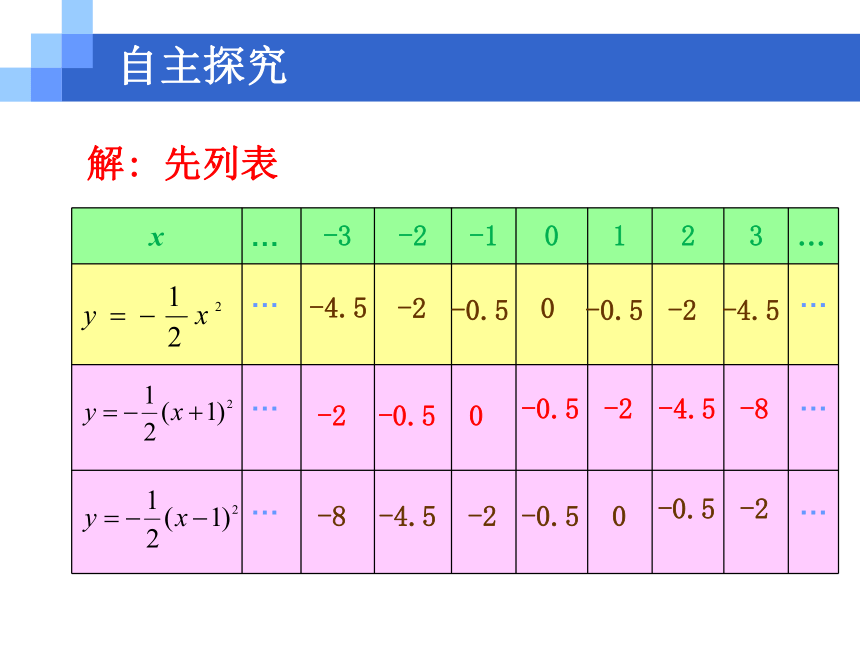
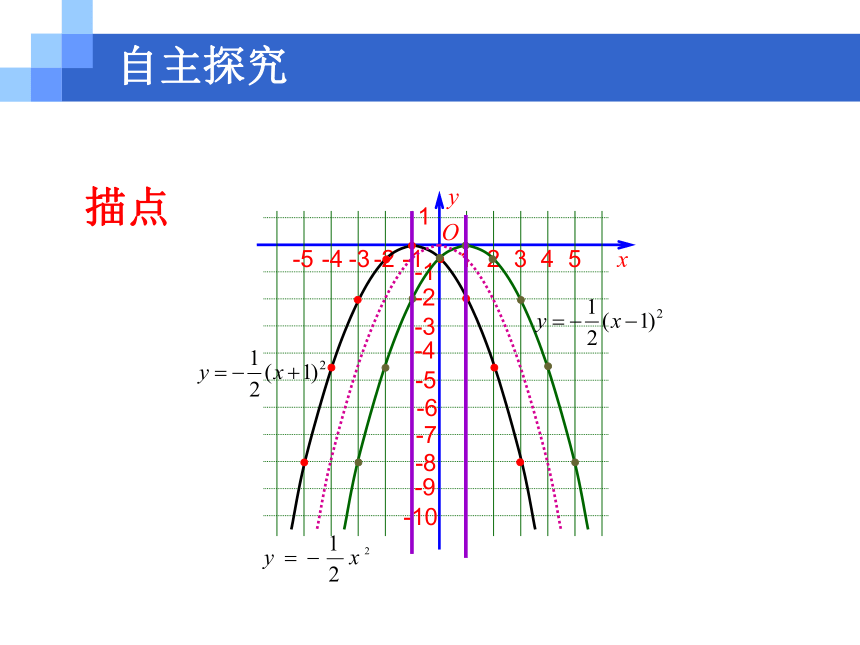
k(k>0)个单位抛物线 y=ax2+k1. 我们已经了解到,函数 y=ax2+k 的图象可由函数y=ax2的图象上下平移得到,平移的规律是怎样的?情境引入2. 函数 的图象,是否也可以由函数 的图象平移得到呢?若是,应该怎样平移?画图试一试,你能从中发现什么规律呢?自主探究自主探究解: 先列表-20-0.5-2-0.5-8-4.5-8-2-0.50-4.5-2-0.5-4.5-0.50-0.5-2-4.5-2自主探究描点自主探究 它们的开口方向都向下,对称轴分别是
y轴、直线x=-1和直线x=1;顶点坐标分别
是(0,0),(-1,0),(1,0).
(2)观察图象探究下列问题:
问题①:观察函数对应值表,你能想象出三个函数图象之间的关系吗?自主探究问题②:抛物线 、
与抛物线 的开口方向、对称轴、
顶点坐标有何异同?
问题③:你能总结出抛物线 y=a(x-h)2有何特点吗? 问题④:对于抛物线 ,当x______时,函数值y随x的增大而减小;当x____时,函数值y随x的增大而增大;当x______时,函数值取得最______值,最______值y=______.
自主探究>-1<-1= -1大大02.观察思考
抛物线 、 与抛物线 有什么关系?
(1)思考抛物线 、 、
的开口方向及大小、对称轴、顶
点位置.
自主探究(2)观察抛物线 , ,
的位置,你有什么发现?与同学交流一下自己的想法.
自主探究 (3) 它们的形状由什么决定?它们的位置关系由什么决定?2. 结论:①自主探究2. 结论:②向左平移1个单位向右平移1个单位即:自主探究3. 思考
(1)如果要得到抛物线 ,应将抛物线 作怎样的平移?
自主探究向右平移4个单位②抛物线y=a(x-h)2可以由抛物线y=ax2向左或向右平移|h|得到.h>0,向右平移;
h<0,向左平移. 一般规律:① y=a(x-h)2(a,h是常数,a≠0)的
图象的开口方向、对称轴、顶点坐标归纳如下:自主探究O自主探究向左平移2个单位向右平移2个单位即:4.应用自主探究例1(补充):不画出图象,你能说明抛物线 y = -3x2与 y= -3(x+2)2 之间的关系吗?解:y= -3x2与 y= -3(x+2)2 的二次项系数都为 -3;两条抛物线的形状相同,开口都向下,顶点分别为(0,0),(-2,0),对称轴分别是y轴和直线 x = -2;抛物线 y = -3(x+2)2 是由抛物线 y= -3x2向左平移2个单位而得到的.巩固练习(1)填空:抛物线 y = (x - 5)2 的开口
_______, 对称轴是__________, 顶点
坐标是______, 它可以看作是由抛物线
y=x2向______平移____个单位得到的.向上x=5(5,0)右5巩固练习022巩固练习答案:列表:向左平移2个单位向右平移2个单位巩固练习xyO巩固练习(1)通过本节课的学习,你有哪些收获?
从二次函数 y=a(x-h)2 的图象形状、画法、对称轴、顶点、开口方向和大小等方面去总结.
(2)你对本节课有什么疑惑?说给老师或同学听听.
总结提高 选做题:
函数 y = - 3(x+1) 2,当x______时,函数值 y 随 x 的增大而减小;当 x______时,函数取得最______值,最______值 y =______.
作业布置>-1=-1大大0谢谢 !
22.1 二次函数的图象和性质
22.1.3 二次函数 y=a(x-h)2+k的图象和性质
第2课时 二次函数 y=a(x-h)2的图象和性质情境引入抛物线之间的平移规律:抛物线 y=ax2抛物线 y=ax2-k向上平移
k(k>0)个单位抛物线 y=ax2向下平移
k(k>0)个单位抛物线 y=ax2+k1. 我们已经了解到,函数 y=ax2+k 的图象可由函数y=ax2的图象上下平移得到,平移的规律是怎样的?情境引入2. 函数 的图象,是否也可以由函数 的图象平移得到呢?若是,应该怎样平移?画图试一试,你能从中发现什么规律呢?自主探究自主探究解: 先列表-20-0.5-2-0.5-8-4.5-8-2-0.50-4.5-2-0.5-4.5-0.50-0.5-2-4.5-2自主探究描点自主探究 它们的开口方向都向下,对称轴分别是
y轴、直线x=-1和直线x=1;顶点坐标分别
是(0,0),(-1,0),(1,0).
(2)观察图象探究下列问题:
问题①:观察函数对应值表,你能想象出三个函数图象之间的关系吗?自主探究问题②:抛物线 、
与抛物线 的开口方向、对称轴、
顶点坐标有何异同?
问题③:你能总结出抛物线 y=a(x-h)2有何特点吗? 问题④:对于抛物线 ,当x______时,函数值y随x的增大而减小;当x____时,函数值y随x的增大而增大;当x______时,函数值取得最______值,最______值y=______.
自主探究>-1<-1= -1大大02.观察思考
抛物线 、 与抛物线 有什么关系?
(1)思考抛物线 、 、
的开口方向及大小、对称轴、顶
点位置.
自主探究(2)观察抛物线 , ,
的位置,你有什么发现?与同学交流一下自己的想法.
自主探究 (3) 它们的形状由什么决定?它们的位置关系由什么决定?2. 结论:①自主探究2. 结论:②向左平移1个单位向右平移1个单位即:自主探究3. 思考
(1)如果要得到抛物线 ,应将抛物线 作怎样的平移?
自主探究向右平移4个单位②抛物线y=a(x-h)2可以由抛物线y=ax2向左或向右平移|h|得到.h>0,向右平移;
h<0,向左平移. 一般规律:① y=a(x-h)2(a,h是常数,a≠0)的
图象的开口方向、对称轴、顶点坐标归纳如下:自主探究O自主探究向左平移2个单位向右平移2个单位即:4.应用自主探究例1(补充):不画出图象,你能说明抛物线 y = -3x2与 y= -3(x+2)2 之间的关系吗?解:y= -3x2与 y= -3(x+2)2 的二次项系数都为 -3;两条抛物线的形状相同,开口都向下,顶点分别为(0,0),(-2,0),对称轴分别是y轴和直线 x = -2;抛物线 y = -3(x+2)2 是由抛物线 y= -3x2向左平移2个单位而得到的.巩固练习(1)填空:抛物线 y = (x - 5)2 的开口
_______, 对称轴是__________, 顶点
坐标是______, 它可以看作是由抛物线
y=x2向______平移____个单位得到的.向上x=5(5,0)右5巩固练习022巩固练习答案:列表:向左平移2个单位向右平移2个单位巩固练习xyO巩固练习(1)通过本节课的学习,你有哪些收获?
从二次函数 y=a(x-h)2 的图象形状、画法、对称轴、顶点、开口方向和大小等方面去总结.
(2)你对本节课有什么疑惑?说给老师或同学听听.
总结提高 选做题:
函数 y = - 3(x+1) 2,当x______时,函数值 y 随 x 的增大而减小;当 x______时,函数取得最______值,最______值 y =______.
作业布置>-1=-1大大0谢谢 !
同课章节目录
