直线与双曲线的位置关系专题讲座
文档属性
| 名称 | 直线与双曲线的位置关系专题讲座 |

|
|
| 格式 | zip | ||
| 文件大小 | 530.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-03 00:00:00 | ||
图片预览




文档简介
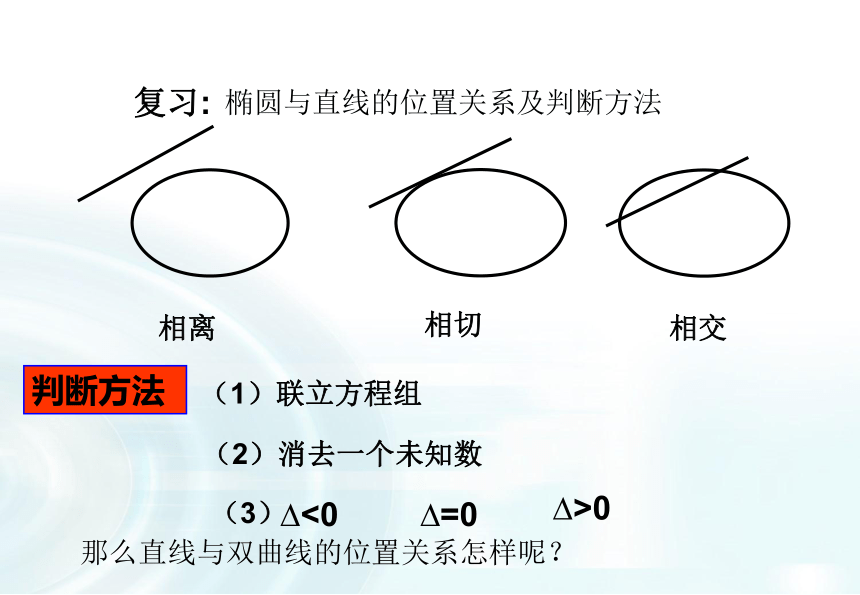
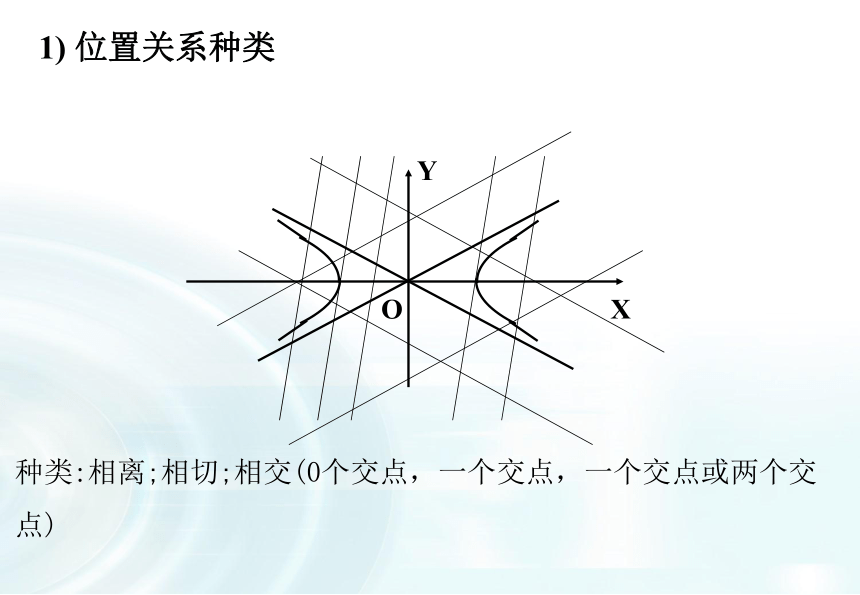
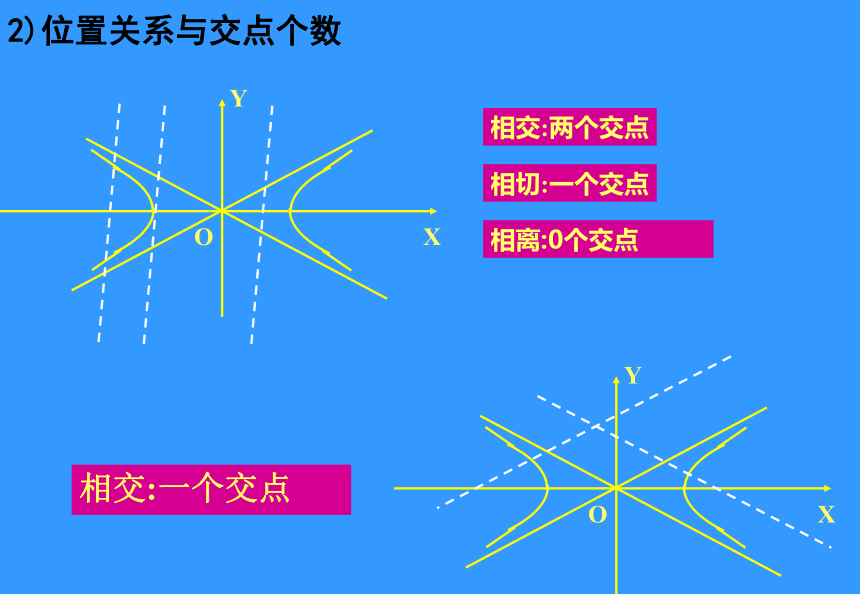
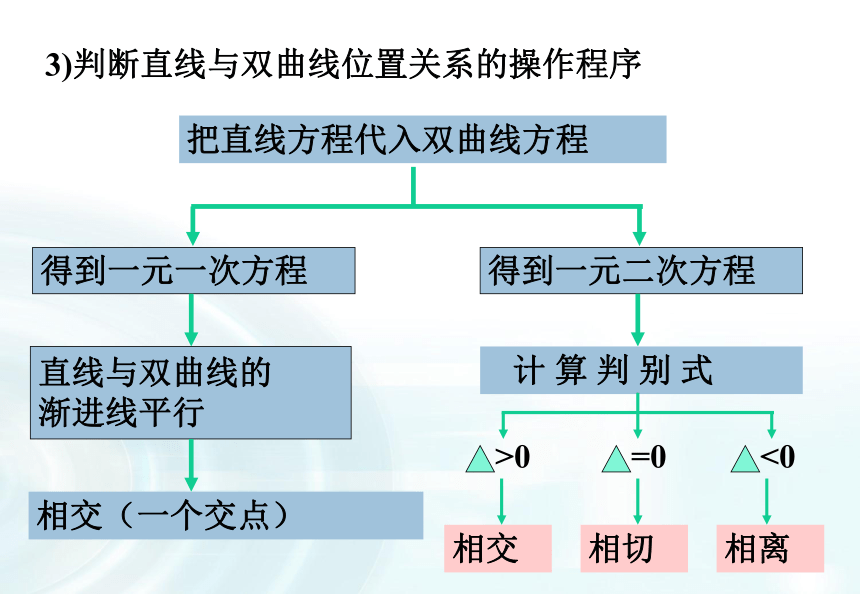
课件27张PPT。直线与双曲线的位置关系专题高中数学教师欧阳文丰制作椭圆与直线的位置关系及判断方法判断方法?<0?=0?>0(1)联立方程组(2)消去一个未知数(3)复习:相离相切相交那么直线与双曲线的位置关系怎样呢?1) 位置关系种类种类:相离;相切;相交(0个交点,一个交点,一个交点或两个交点)2)位置关系与交点个数相离:0个交点相交:一个交点相交:两个交点相切:一个交点3)判断直线与双曲线位置关系的操作程序把直线方程代入双曲线方程得到一元一次方程得到一元二次方程直线与双曲线的
渐进线平行相交(一个交点) 计 算 判 别 式(b2-a2k2)x2-2kma2x+a2(m2+b2)=01.二次项系数为0时,L与双曲线的渐近线平行或重合。
重合:无交点;平行:有一个交点。2.二次项系数不为0时,上式为一元二次方程,②相切一点: △=0
③相 离: △<0 注:特别注意直线与双曲线的位置关系中:
一解不一定相切,相交不一定两解,两解不一定同支例1.已知直线y=kx-1与双曲线x2-y2=4,试讨论实数k
的取值范围,使直线与双曲线
(1)没有公共点;
(2)有两个公共点;
(3)只有一个公共点;
(4)交于异支两点;
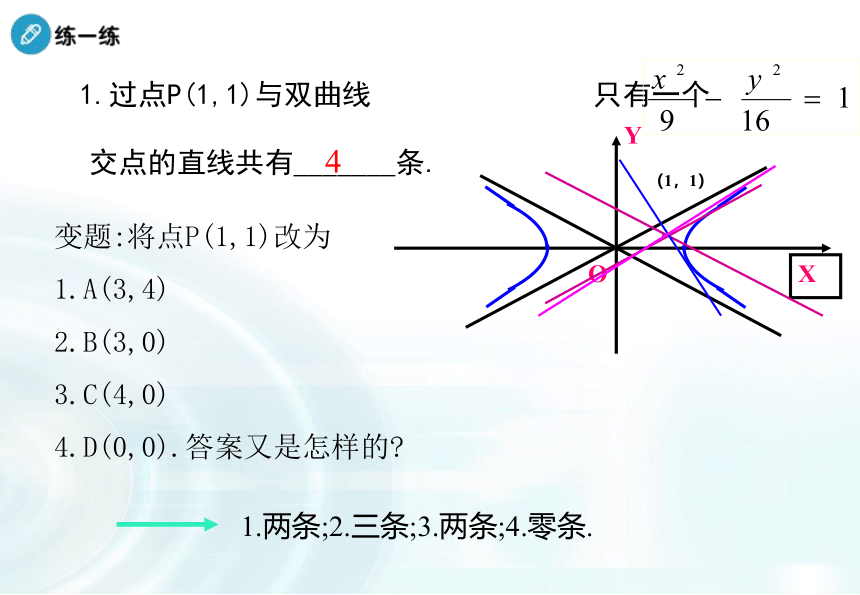
(5)与左支交于两点.-1<k<1 ;1.过点P(1,1)与双曲线 只有一个变题:将点P(1,1)改为
1.A(3,4)
2.B(3,0)
3.C(4,0)
4.D(0,0).答案又是怎样的?41.两条;2.三条;3.两条;4.零条.交点的直线共有_______条.(1,1)。分析:求弦长问题有两种方法:
法一:如果交点坐标易求,可直接用两点间距离公式代入求弦长;
法二:但有时为了简化计算,常设而不求,运用韦达定理来处理.解:由双曲线的方程得,两焦点分别为F1(-3,0),F2(3,0).因为直线AB的倾斜角是30°,且直线经过右焦点F2,所以,直线AB的方程为【提升总结】这里我们也可以利用弦长公式求解:弦长公式:或算一算,看结果一样吗?点差法例4韦达定理1 .位置判定
2.弦长公式
3.中点问题
4.垂直与对称
5.设而不求(韦达定理、点差法)
渐进线平行相交(一个交点) 计 算 判 别 式(b2-a2k2)x2-2kma2x+a2(m2+b2)=01.二次项系数为0时,L与双曲线的渐近线平行或重合。
重合:无交点;平行:有一个交点。2.二次项系数不为0时,上式为一元二次方程,②相切一点: △=0
③相 离: △<0 注:特别注意直线与双曲线的位置关系中:
一解不一定相切,相交不一定两解,两解不一定同支例1.已知直线y=kx-1与双曲线x2-y2=4,试讨论实数k
的取值范围,使直线与双曲线
(1)没有公共点;
(2)有两个公共点;
(3)只有一个公共点;
(4)交于异支两点;
(5)与左支交于两点.-1<k<1 ;1.过点P(1,1)与双曲线 只有一个变题:将点P(1,1)改为
1.A(3,4)
2.B(3,0)
3.C(4,0)
4.D(0,0).答案又是怎样的?41.两条;2.三条;3.两条;4.零条.交点的直线共有_______条.(1,1)。分析:求弦长问题有两种方法:
法一:如果交点坐标易求,可直接用两点间距离公式代入求弦长;
法二:但有时为了简化计算,常设而不求,运用韦达定理来处理.解:由双曲线的方程得,两焦点分别为F1(-3,0),F2(3,0).因为直线AB的倾斜角是30°,且直线经过右焦点F2,所以,直线AB的方程为【提升总结】这里我们也可以利用弦长公式求解:弦长公式:或算一算,看结果一样吗?点差法例4韦达定理1 .位置判定
2.弦长公式
3.中点问题
4.垂直与对称
5.设而不求(韦达定理、点差法)
