福建省泉州市泉港区2017-2018学年度七年级数学上第4章《图形的初步认识》检测题含答案解析
文档属性
| 名称 | 福建省泉州市泉港区2017-2018学年度七年级数学上第4章《图形的初步认识》检测题含答案解析 |
|
|
| 格式 | zip | ||
| 文件大小 | 330.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-02 00:00:00 | ||
图片预览

文档简介
第4章
图形的初步认识检测题
(时间:90分钟,满分:100分)
一、选择题(每小题3分,共30分)
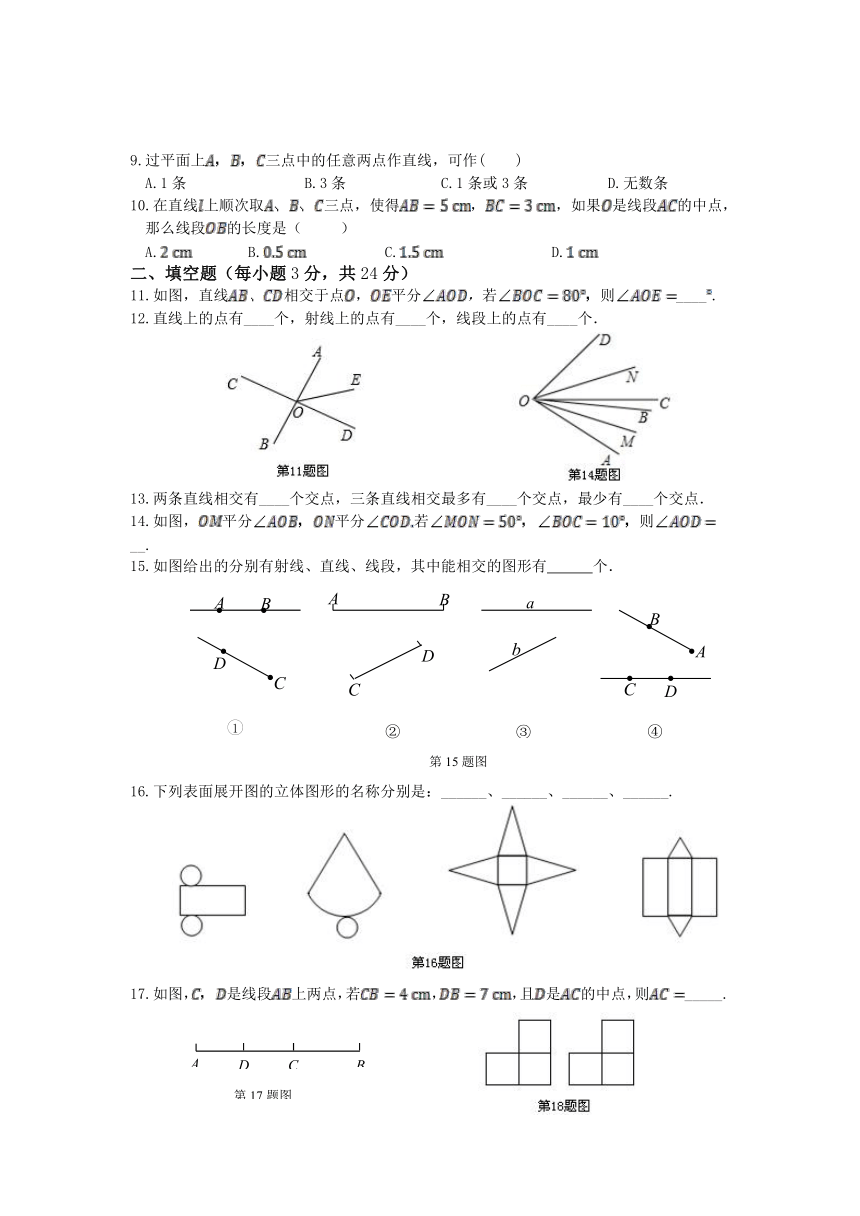
1.下列物体的形状类似于球的是( )
A.茶杯
B.羽毛球
C.乒乓球
D.白炽灯泡
2.正多面体的面数、棱数、顶点数之间存在着一个奇妙的关系,若用分别表示正多面体的面数、棱数、顶点数,则有,现有一个正多面体共有12条棱,6个顶点,则它的面数等于( )
A.6
B.8
C.12
D.20
3.如果与是邻补角,且,那么的余角是(
)
A.
B.
C.
D.不能确定
4.下列四个立体图形中,主视图为圆的是( )
A.
B.
C.
D.
5.将“创建文明城市”六个字分别写在一个正方体的六个面上,这个正方体的平面展开图如图所示,那么在这个正方体中,和“创”相对的字是( )
A.文
B.明
C.城
D.市
6.如图,已知直线相交于点,平分,,则的大小
为( )
A.
B.
C.
D.
7.圆柱的侧面展开图可能是(
)
8.下列平面图形不能够围成正方体的是(
)
9.过平面上三点中的任意两点作直线,可作( )
A.1条
B.3条
C.1条或3条
D.无数条
10.在直线上顺次取三点,使得,,如果是线段的中点,那么线段的长度是(
)
A.
B.
C.
D.
二、填空题(每小题3分,共24分)
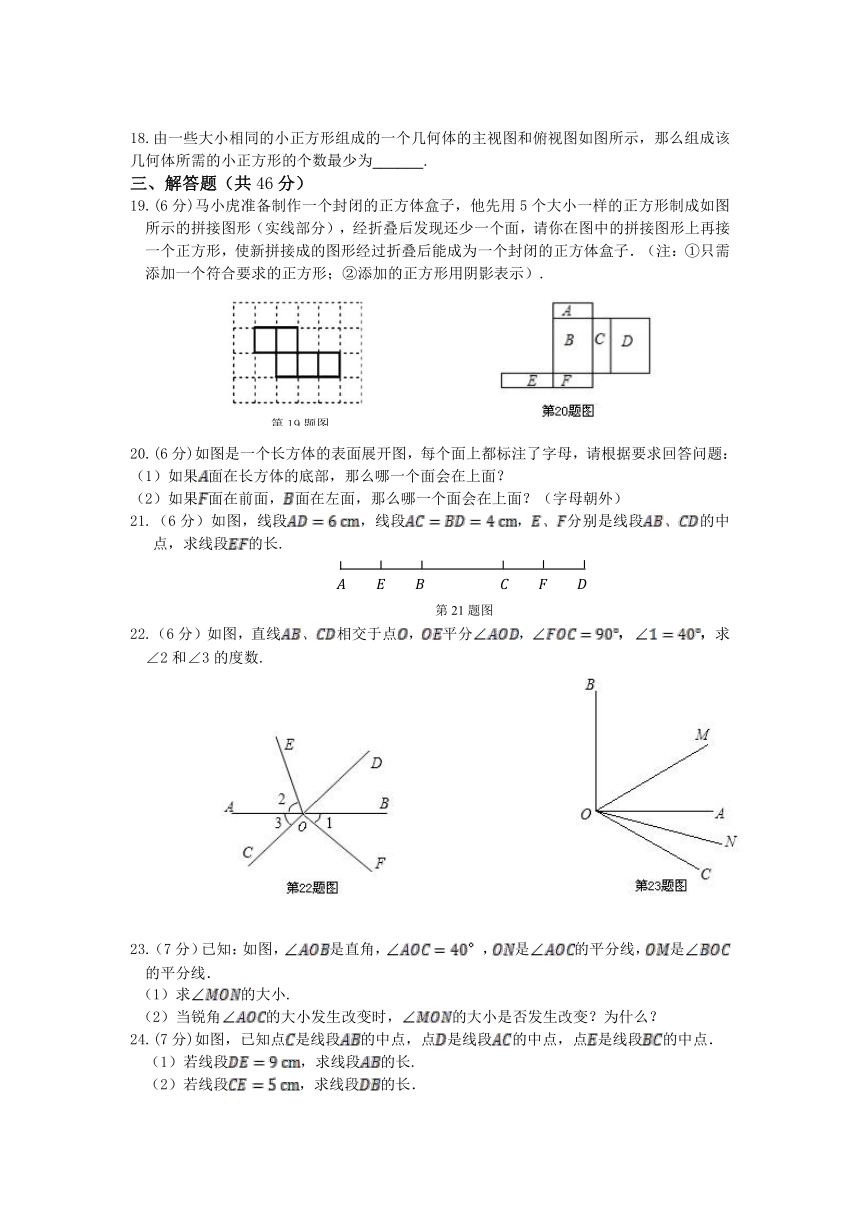
11.如图,直线相交于点,平分,若则____.
12.直线上的点有____个,射线上的点有____个,线段上的点有____个.
13.两条直线相交有____个交点,三条直线相交最多有____个交点,最少有____个交点.
14.如图,平分平分若则
__.
15.如图给出的分别有射线、直线、线段,其中能相交的图形有 个.
16.下列表面展开图的立体图形的名称分别是:______、______、______、______.
17.如图,是线段上两点,若,,且是的中点,则_____.
18.由一些大小相同的小正方形组成的一个几何体的主视图和俯视图如图所示,那么组成该几何体所需的小正方形的个数最少为______.
三、解答题(共46分)
19.(6分)马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(注:①只需添加一个符合要求的正方形;②添加的正方形用阴影表示).
20.(6分)如图是一个长方体的表面展开图,每个面上都标注了字母,请根据要求回答问题:
(1)如果面在长方体的底部,那么哪一个面会在上面?
(2)如果面在前面,面在左面,那么哪一个面会在上面?(字母朝外)
21.(6分)如图,线段,线段,分别是线段的中点,求线段的长.
22.(6分)如图,直线相交于点,平分,求∠2和∠3的度数.
23.(7分)已知:如图,是直角,,是的平分线,是的平分线.
(1)求的大小.
(2)当锐角的大小发生改变时,的大小是否发生改变?为什么?
24.(7分)如图,已知点是线段的中点,点是线段的中点,点是线段的中点.
(1)若线段,求线段的长.
(2)若线段,求线段的长.
25.(8分)十八世纪瑞士数学家欧拉证明了简单多面体中顶点数()、面数()、棱数()之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:
(1)根据上面多面体模型,完成表格中的空格:
多面体
顶点数()
面数()
棱数()
四面体
4
4
长方体
8
6
12
正八面体
8
12
正十二面体
20
12
30
你发现顶点数()、面数()、棱数()之间存在的关系式是______;
(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是______;
(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱,设该多面体外表三角形的个数为个,八边形的个数为个,求的值.
第4章
图形的初步认识检测题参考答案
1.C
解析:根据生活常识可知乒乓球是球体.故选C.
2.B
解析:因为正多面体共有12条棱,6个顶点,所以,
所以.故选B.
3.C
解析:与是邻补角,所以.
所以的余角是,故选C.
4.B
解析:A.主视图是正方形,故此选项错误;B.主视图是圆,故此选项正确;
C.主视图是三角形,故此选项错误;D.主视图是长方形,故此选项错误.
5.B
解析:结合展开图可知,与“创”相对的字是“明”.故选B.
6.D
解析:因为
平分所以
所以故选D.
7.B
解析:圆柱的侧面展开图是长方形,故选B.
8.B
解析:利用自己的空间想象能力或者自己动手实践一下,可知答案选B.
9.C
解析:当三点共线时,可以作1条直线;当三点不共线时,可以作3条直线.
10.D
解析:因为是在直线上顺次取三点,所以.
因为是线段的中点,所以
所以.
故选D.
11.
解析:因为,所以.
因为平分,所以.
12.无数
无数
无数
解析:直线、射线、线段都是由无数个点组成的.
13.1
3
1
解析:两条直线相交有且只有1个交点;三条直线两两相交且不交于一点时,有3个交点;当三条直线交于同一点时,有1个交点.
14.
90°
解析:因为平分,平分,
所以
因为
所以即.
所以.
15.2
解析:①③能相交,②④不能相交.
16.圆柱
圆锥
四棱锥
三棱柱
17.
解析:因为点是线段的中点,所以.
因为,,所以,所以.
18.4
解析:由题中所给出的主视图知物体共两列,且左侧一列高一层,右侧一列最高两层;由俯视图可知左侧一行,右侧两行,于是,可确定左侧只有一个小正方体,而右侧可能是一行单层一行两层,还可能两行都是两层.所以图中的小正方体最少块,最多块.
19.解:答案不唯一,如图.
20.解:(1)因为面“”与面“”相对,所以面在长方体的底部时,面在上面.
(2)由图可知,如果面在前面,面在左面,那么“”面在下面.
由图可知,面“”与面“”相对,所以面会在上面.
21.解:因为线段,线段,
所以
所以
又因为分别是线段的中点,
所以
所以
所以
答:线段的长为.
22.解:因为为直线,
所以所以
因为与互补,所以
因为平分,所以
23.解:(1)因为是直角,,
所以
因为是的平分线,是的平分线,
所以
所以
(2)当锐角∠AOC的大小发生改变时,∠MON的大小不发生改变.
因为
又,所以
24.解:(1)因为点是线段的中点,点是线段的中点,
所以,,
所以.
(2)因为点是线段的中点,所以.
因为点是线段的中点,点是线段的中点,
所以,所以.
25.解:(1)四面体的棱数为6;正八面体的顶点数为6;关系式为:.
多面体
顶点数()
面数()
棱数()
四面体
4
4
6
长方体
8
6
12
正八面体
6
8
12
正十二面体
20
12
30
(2)由题意得:,解得.
(3)因为有24个顶点,每个顶点处都有3条棱,两点确定一条直线,
所以共有棱,那么,解得,所以.
A
B
C
D
A
B
D
C
②
③
④
第15题图
第17题图
A
B
D
C
第19题图.为相反数
第21题图
A
E
B
C
F
D
第19题答图
图形的初步认识检测题
(时间:90分钟,满分:100分)
一、选择题(每小题3分,共30分)
1.下列物体的形状类似于球的是( )
A.茶杯
B.羽毛球
C.乒乓球
D.白炽灯泡
2.正多面体的面数、棱数、顶点数之间存在着一个奇妙的关系,若用分别表示正多面体的面数、棱数、顶点数,则有,现有一个正多面体共有12条棱,6个顶点,则它的面数等于( )
A.6
B.8
C.12
D.20
3.如果与是邻补角,且,那么的余角是(
)
A.
B.
C.
D.不能确定
4.下列四个立体图形中,主视图为圆的是( )
A.
B.
C.
D.
5.将“创建文明城市”六个字分别写在一个正方体的六个面上,这个正方体的平面展开图如图所示,那么在这个正方体中,和“创”相对的字是( )
A.文
B.明
C.城
D.市
6.如图,已知直线相交于点,平分,,则的大小
为( )
A.
B.
C.
D.
7.圆柱的侧面展开图可能是(
)
8.下列平面图形不能够围成正方体的是(
)
9.过平面上三点中的任意两点作直线,可作( )
A.1条
B.3条
C.1条或3条
D.无数条
10.在直线上顺次取三点,使得,,如果是线段的中点,那么线段的长度是(
)
A.
B.
C.
D.
二、填空题(每小题3分,共24分)
11.如图,直线相交于点,平分,若则____.
12.直线上的点有____个,射线上的点有____个,线段上的点有____个.
13.两条直线相交有____个交点,三条直线相交最多有____个交点,最少有____个交点.
14.如图,平分平分若则
__.
15.如图给出的分别有射线、直线、线段,其中能相交的图形有 个.
16.下列表面展开图的立体图形的名称分别是:______、______、______、______.
17.如图,是线段上两点,若,,且是的中点,则_____.
18.由一些大小相同的小正方形组成的一个几何体的主视图和俯视图如图所示,那么组成该几何体所需的小正方形的个数最少为______.
三、解答题(共46分)
19.(6分)马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(注:①只需添加一个符合要求的正方形;②添加的正方形用阴影表示).
20.(6分)如图是一个长方体的表面展开图,每个面上都标注了字母,请根据要求回答问题:
(1)如果面在长方体的底部,那么哪一个面会在上面?
(2)如果面在前面,面在左面,那么哪一个面会在上面?(字母朝外)
21.(6分)如图,线段,线段,分别是线段的中点,求线段的长.
22.(6分)如图,直线相交于点,平分,求∠2和∠3的度数.
23.(7分)已知:如图,是直角,,是的平分线,是的平分线.
(1)求的大小.
(2)当锐角的大小发生改变时,的大小是否发生改变?为什么?
24.(7分)如图,已知点是线段的中点,点是线段的中点,点是线段的中点.
(1)若线段,求线段的长.
(2)若线段,求线段的长.
25.(8分)十八世纪瑞士数学家欧拉证明了简单多面体中顶点数()、面数()、棱数()之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:
(1)根据上面多面体模型,完成表格中的空格:
多面体
顶点数()
面数()
棱数()
四面体
4
4
长方体
8
6
12
正八面体
8
12
正十二面体
20
12
30
你发现顶点数()、面数()、棱数()之间存在的关系式是______;
(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是______;
(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱,设该多面体外表三角形的个数为个,八边形的个数为个,求的值.
第4章
图形的初步认识检测题参考答案
1.C
解析:根据生活常识可知乒乓球是球体.故选C.
2.B
解析:因为正多面体共有12条棱,6个顶点,所以,
所以.故选B.
3.C
解析:与是邻补角,所以.
所以的余角是,故选C.
4.B
解析:A.主视图是正方形,故此选项错误;B.主视图是圆,故此选项正确;
C.主视图是三角形,故此选项错误;D.主视图是长方形,故此选项错误.
5.B
解析:结合展开图可知,与“创”相对的字是“明”.故选B.
6.D
解析:因为
平分所以
所以故选D.
7.B
解析:圆柱的侧面展开图是长方形,故选B.
8.B
解析:利用自己的空间想象能力或者自己动手实践一下,可知答案选B.
9.C
解析:当三点共线时,可以作1条直线;当三点不共线时,可以作3条直线.
10.D
解析:因为是在直线上顺次取三点,所以.
因为是线段的中点,所以
所以.
故选D.
11.
解析:因为,所以.
因为平分,所以.
12.无数
无数
无数
解析:直线、射线、线段都是由无数个点组成的.
13.1
3
1
解析:两条直线相交有且只有1个交点;三条直线两两相交且不交于一点时,有3个交点;当三条直线交于同一点时,有1个交点.
14.
90°
解析:因为平分,平分,
所以
因为
所以即.
所以.
15.2
解析:①③能相交,②④不能相交.
16.圆柱
圆锥
四棱锥
三棱柱
17.
解析:因为点是线段的中点,所以.
因为,,所以,所以.
18.4
解析:由题中所给出的主视图知物体共两列,且左侧一列高一层,右侧一列最高两层;由俯视图可知左侧一行,右侧两行,于是,可确定左侧只有一个小正方体,而右侧可能是一行单层一行两层,还可能两行都是两层.所以图中的小正方体最少块,最多块.
19.解:答案不唯一,如图.
20.解:(1)因为面“”与面“”相对,所以面在长方体的底部时,面在上面.
(2)由图可知,如果面在前面,面在左面,那么“”面在下面.
由图可知,面“”与面“”相对,所以面会在上面.
21.解:因为线段,线段,
所以
所以
又因为分别是线段的中点,
所以
所以
所以
答:线段的长为.
22.解:因为为直线,
所以所以
因为与互补,所以
因为平分,所以
23.解:(1)因为是直角,,
所以
因为是的平分线,是的平分线,
所以
所以
(2)当锐角∠AOC的大小发生改变时,∠MON的大小不发生改变.
因为
又,所以
24.解:(1)因为点是线段的中点,点是线段的中点,
所以,,
所以.
(2)因为点是线段的中点,所以.
因为点是线段的中点,点是线段的中点,
所以,所以.
25.解:(1)四面体的棱数为6;正八面体的顶点数为6;关系式为:.
多面体
顶点数()
面数()
棱数()
四面体
4
4
6
长方体
8
6
12
正八面体
6
8
12
正十二面体
20
12
30
(2)由题意得:,解得.
(3)因为有24个顶点,每个顶点处都有3条棱,两点确定一条直线,
所以共有棱,那么,解得,所以.
A
B
C
D
A
B
D
C
②
③
④
第15题图
第17题图
A
B
D
C
第19题图.为相反数
第21题图
A
E
B
C
F
D
第19题答图
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
