2017年秋人教版九年级上册数学课件22.3.1用二次函数解决利润等代数问题 课件
文档属性
| 名称 | 2017年秋人教版九年级上册数学课件22.3.1用二次函数解决利润等代数问题 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 142.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-02 00:00:00 | ||
图片预览








文档简介
课件24张PPT。第二十二章 二次函数
22.3 实际问题与二次函数
第1课时 用二次函数解决利润等代数问题创设情境,引出问题1.二次函数 (a≠0)有哪些性质?(着重回忆“顶点”“增减性”)
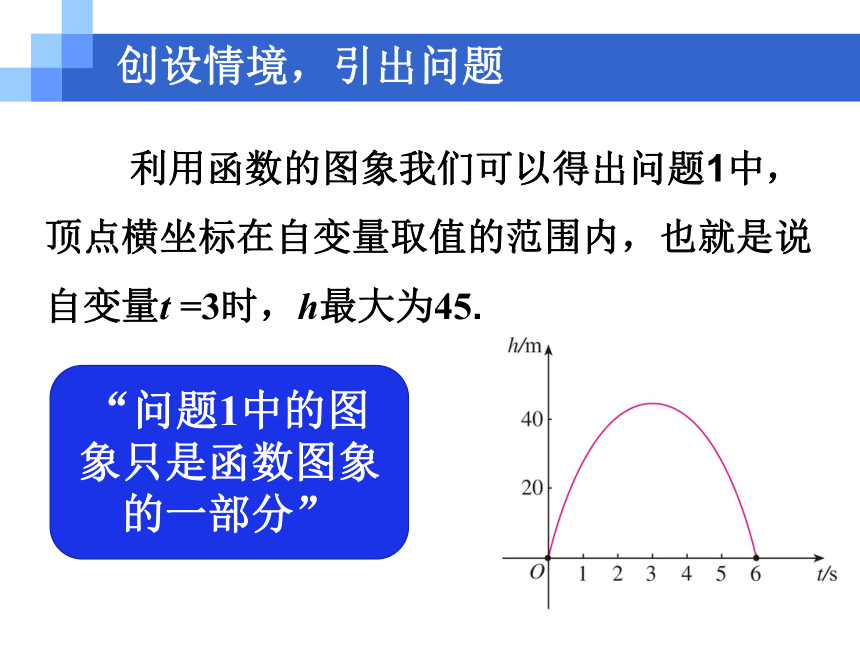
2.我们能否用二次函数的图象与性质解决实际生活问题呢?请看如下问题:创设情境,引出问题问题1:从地面竖直向上抛出一个小球,小球的高度 h(单位:m)与小球的运动时间 t(单位:s)之间的关系式是h= 30t - 5t 2 (0≤t≤6).小球的运动时间是多少时,小球最高?小球运动中的最大高度是多少?创设情境,引出问题 利用函数的图象我们可以得出问题1中,顶点横坐标在自变量取值的范围内,也就是说自变量t =3时,h最大为45.“问题1中的图象只是函数图象的一部分” 一般地,当a>0(a<0)时抛物线
(a≠0)的顶点是最低(高)点,也就是函数的最值.适时小结 问:如何理解“一般地”?适时小结 主要看顶点的横坐标是否在实际问题中自变量的取值范围内. 利用二次函数可以解决利润等代数问题.问题探究问题2:某商品现在的售价为每件60元,经过市场调查,商家决定提高售价,同时销售数量 y(件)与销售单价x(元)之间的函数关系为 y= -10x+900,已知该商品的进价为每件40元,如何定价才能使利润最大?问题探究分析: 提问1:问题中的“定价”是指售价 还是进价?是指售价60元吗?
提问2:如何表示利润?
利润=售价×数量-进价×数量
利润=(售价-进价)×数量问题探究 提问3:可否写出利润的函数表达式? 设利润为w元,可得
w = (x-40)(-10x+900) 提问4:根据题目要求可否得到自变量x的取值范围?60≤x≤90问题探究 提问5:当x=______时, w最大.
x =65问题探究问题3:某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映,如果调整价格,每涨价1元,每星期要少卖出10件,已知该商品的进价为每件40元,如何定价才能使利润最大?问题探究分析:提问1:如何理解“每涨1元,每星期要少卖出10件” ?能否用具体售价解答此问题?
问题探究提问2:当售价为每件70元时,涨价多少?数量怎样变化?数量是升高还是降低?是在谁的基础上变化?涨价10元减少(x-60) ×10件问题探究提问3:当售价每件x元,如何表示数量?
问题探究 提问4:如何表示利润w元?
问题探究提问5:可否根据题意得到自变量x的取值范围?
问题探究提问6:当x=_____时, w最大,最大为_______.
当x =65时,w最大,最大为6 250.问题探究变式问题1: 若只将问题3中 “每涨价1元,每星期要少卖出10件”改为 “每降价1元,每星期要多卖出20件” ,如何定价才能使利润最大?问:此时的数量如何表示?问题探究变式问题2: 若只将问题3中 “每涨价1元,每星期要少卖出10件”改为 “每涨价2元,每星期要少卖出10件” ,如何定价才能使利润最大?问:此时的数量如何表示?回归教材请同学们阅读教材第50页探究2的解答:(1)讨论两种解法的异同;
(2)书面解答探究2.巩固练习 某商店经营一种小商品,进价为每件2.5元,据市场调查,销售单价是13.5元
时平均每天的销量是500件,而销售价每降低1元,平均每天就可以多卖出100件. (1)假定每件商品降价x元,商店每天销售这种小商品的利润是y元,请写出y与x的之间函数关系式,并注明x的取值范围;巩固练习 (2)每件小商品的销售价是多少时,商店每天销售这种小商品的利润最大?最大利润是多少?
(注:销售利润=销售收入-购进成本)(2)当x =3时,ymax=6 400(1)y =-100x2+600+5 500(01.可以用二次函数解决生活中的利润问题.
2.在实际问题中求解的二次函数的最值,不一定都在函数图象的顶点处取得.作业:
教材第51~52页习题22.3第1~ 3题,第8题.
谢谢 !
22.3 实际问题与二次函数
第1课时 用二次函数解决利润等代数问题创设情境,引出问题1.二次函数 (a≠0)有哪些性质?(着重回忆“顶点”“增减性”)
2.我们能否用二次函数的图象与性质解决实际生活问题呢?请看如下问题:创设情境,引出问题问题1:从地面竖直向上抛出一个小球,小球的高度 h(单位:m)与小球的运动时间 t(单位:s)之间的关系式是h= 30t - 5t 2 (0≤t≤6).小球的运动时间是多少时,小球最高?小球运动中的最大高度是多少?创设情境,引出问题 利用函数的图象我们可以得出问题1中,顶点横坐标在自变量取值的范围内,也就是说自变量t =3时,h最大为45.“问题1中的图象只是函数图象的一部分” 一般地,当a>0(a<0)时抛物线
(a≠0)的顶点是最低(高)点,也就是函数的最值.适时小结 问:如何理解“一般地”?适时小结 主要看顶点的横坐标是否在实际问题中自变量的取值范围内. 利用二次函数可以解决利润等代数问题.问题探究问题2:某商品现在的售价为每件60元,经过市场调查,商家决定提高售价,同时销售数量 y(件)与销售单价x(元)之间的函数关系为 y= -10x+900,已知该商品的进价为每件40元,如何定价才能使利润最大?问题探究分析: 提问1:问题中的“定价”是指售价 还是进价?是指售价60元吗?
提问2:如何表示利润?
利润=售价×数量-进价×数量
利润=(售价-进价)×数量问题探究 提问3:可否写出利润的函数表达式? 设利润为w元,可得
w = (x-40)(-10x+900) 提问4:根据题目要求可否得到自变量x的取值范围?60≤x≤90问题探究 提问5:当x=______时, w最大.
x =65问题探究问题3:某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映,如果调整价格,每涨价1元,每星期要少卖出10件,已知该商品的进价为每件40元,如何定价才能使利润最大?问题探究分析:提问1:如何理解“每涨1元,每星期要少卖出10件” ?能否用具体售价解答此问题?
问题探究提问2:当售价为每件70元时,涨价多少?数量怎样变化?数量是升高还是降低?是在谁的基础上变化?涨价10元减少(x-60) ×10件问题探究提问3:当售价每件x元,如何表示数量?
问题探究 提问4:如何表示利润w元?
问题探究提问5:可否根据题意得到自变量x的取值范围?
问题探究提问6:当x=_____时, w最大,最大为_______.
当x =65时,w最大,最大为6 250.问题探究变式问题1: 若只将问题3中 “每涨价1元,每星期要少卖出10件”改为 “每降价1元,每星期要多卖出20件” ,如何定价才能使利润最大?问:此时的数量如何表示?问题探究变式问题2: 若只将问题3中 “每涨价1元,每星期要少卖出10件”改为 “每涨价2元,每星期要少卖出10件” ,如何定价才能使利润最大?问:此时的数量如何表示?回归教材请同学们阅读教材第50页探究2的解答:(1)讨论两种解法的异同;
(2)书面解答探究2.巩固练习 某商店经营一种小商品,进价为每件2.5元,据市场调查,销售单价是13.5元
时平均每天的销量是500件,而销售价每降低1元,平均每天就可以多卖出100件. (1)假定每件商品降价x元,商店每天销售这种小商品的利润是y元,请写出y与x的之间函数关系式,并注明x的取值范围;巩固练习 (2)每件小商品的销售价是多少时,商店每天销售这种小商品的利润最大?最大利润是多少?
(注:销售利润=销售收入-购进成本)(2)当x =3时,ymax=6 400(1)y =-100x2+600+5 500(0
2.在实际问题中求解的二次函数的最值,不一定都在函数图象的顶点处取得.作业:
教材第51~52页习题22.3第1~ 3题,第8题.
谢谢 !
同课章节目录
