2017年秋人教版九年级上册数学课件23.1 图形的旋转 课件
文档属性
| 名称 | 2017年秋人教版九年级上册数学课件23.1 图形的旋转 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-02 17:01:10 | ||
图片预览






文档简介
课件22张PPT。第二十三章 旋转
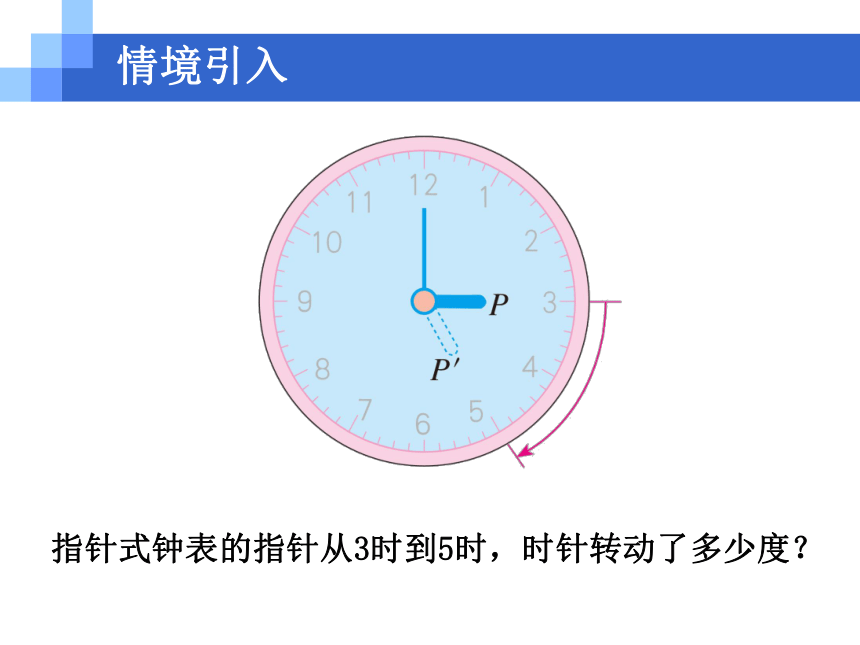
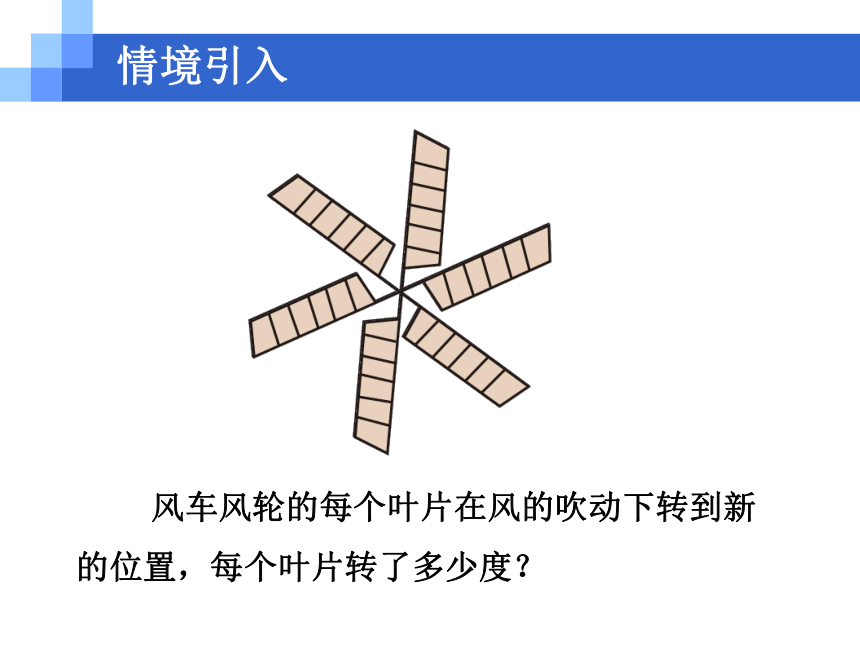
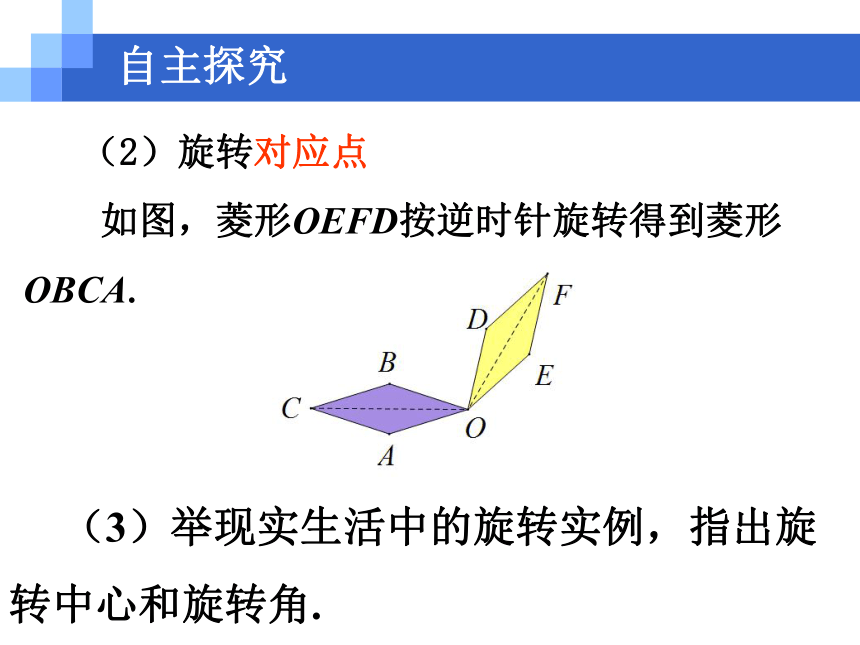
23.1 图形的旋转情境引入观察图片 指针式钟表的指针从3时到5时,时针转动了多少度?情境引入 奔驰车标志旋转多少度能够重合?情境引入 风车风轮的每个叶片在风的吹动下转到新的位置,每个叶片转了多少度?情境引入自主探究1.概念认识 (1)把一个平面图形绕着平面内某一点 O 转动一个角度,叫做图形的旋转,点 O 叫做旋转中心,转动的角叫做旋转角. 自主探究 (2)旋转对应点
如图,菱形OEFD按逆时针旋转得到菱形OBCA. (3)举现实生活中的旋转实例,指出旋转中心和旋转角.自主探究2.旋转性质的探索 在硬纸板上挖一个三角形洞,再用针钉住一点作为旋转中心,硬纸板下面放一张白纸, 先在纸上描出这个挖掉的三角形图案(△ABC), 然后围绕旋转中心转动硬纸板,
再描出这个挖掉的三角形
(△A′B′C′),移开硬纸板.自主探究(1)线段 OA 和 OA′,OB和 OB′,OC 和 OC′
有什么关系?试探讨:(2)∠AOA',∠BOB'和∠COC'有什么关系? ∠ AOA' =∠BOB'=∠COC' OA = OA′,OB= OB′,OC = OC′自主探究(3)△ABC和△A'B'C'的形状和大小有什么关系?△ABC≌△A'B'C'自主探究◆ 对应点到旋转中心的距离相等.
◆ 对应点与旋转中心所连线段的夹角等于
旋转角.
◆ 旋转前、后的图形全等.旋转的性质自主探究3.实践操作问题:(1)已知点A和点A外一点O,你能画出点A绕点O旋转100°的对应点B吗?
自主探究画法:在 A点的右侧作∠AOM=100°,在OM
上截取OB=OA,则B点即为所求.分析:根据旋转性质知道,OA =OB,且∠AOB =100°,怎样找到B点?自主探究(2)已知:如图,四边形 ABCD 和四边形外一点 O, 你能作出以O为旋转中心的旋转图形吗?分析:能.如图(1),以O为旋转中心,顺时针旋转40°.如图(2),以O为旋转中心,顺时针旋转60°.自主探究(1)(2)自主探究 归纳:(1)作图的三要素:旋转中心,旋转角,旋转
方向.
(2)关键是运用性质找出对应点.
(3)旋转中心、旋转角、旋转方向不同,得到
的同一图形的旋转图形的位置不同,但都全等.自主探究4.性质的应用例 如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.巩固练习(1)教材第59页练习2.(2)教材第61页练习第1、2题.(3)教材第62页练习.巩固练习补充练习:
已知:△ABC以C为旋转中心,画出逆时
针旋转90°后的旋转图形.总结提高(1)旋转定义.1.小结(2)旋转性质.(3)旋转作图.2.布置作业
(1)教材第62页习题23.1第4题(必做).
(2)教材第62页习题23.1第1题(选做).
(3)教材第63页习题23.1第5、6、7题.
(4)教材第63页习题23.1第8、9题.总结提高谢谢 !
23.1 图形的旋转情境引入观察图片 指针式钟表的指针从3时到5时,时针转动了多少度?情境引入 奔驰车标志旋转多少度能够重合?情境引入 风车风轮的每个叶片在风的吹动下转到新的位置,每个叶片转了多少度?情境引入自主探究1.概念认识 (1)把一个平面图形绕着平面内某一点 O 转动一个角度,叫做图形的旋转,点 O 叫做旋转中心,转动的角叫做旋转角. 自主探究 (2)旋转对应点
如图,菱形OEFD按逆时针旋转得到菱形OBCA. (3)举现实生活中的旋转实例,指出旋转中心和旋转角.自主探究2.旋转性质的探索 在硬纸板上挖一个三角形洞,再用针钉住一点作为旋转中心,硬纸板下面放一张白纸, 先在纸上描出这个挖掉的三角形图案(△ABC), 然后围绕旋转中心转动硬纸板,
再描出这个挖掉的三角形
(△A′B′C′),移开硬纸板.自主探究(1)线段 OA 和 OA′,OB和 OB′,OC 和 OC′
有什么关系?试探讨:(2)∠AOA',∠BOB'和∠COC'有什么关系? ∠ AOA' =∠BOB'=∠COC' OA = OA′,OB= OB′,OC = OC′自主探究(3)△ABC和△A'B'C'的形状和大小有什么关系?△ABC≌△A'B'C'自主探究◆ 对应点到旋转中心的距离相等.
◆ 对应点与旋转中心所连线段的夹角等于
旋转角.
◆ 旋转前、后的图形全等.旋转的性质自主探究3.实践操作问题:(1)已知点A和点A外一点O,你能画出点A绕点O旋转100°的对应点B吗?
自主探究画法:在 A点的右侧作∠AOM=100°,在OM
上截取OB=OA,则B点即为所求.分析:根据旋转性质知道,OA =OB,且∠AOB =100°,怎样找到B点?自主探究(2)已知:如图,四边形 ABCD 和四边形外一点 O, 你能作出以O为旋转中心的旋转图形吗?分析:能.如图(1),以O为旋转中心,顺时针旋转40°.如图(2),以O为旋转中心,顺时针旋转60°.自主探究(1)(2)自主探究 归纳:(1)作图的三要素:旋转中心,旋转角,旋转
方向.
(2)关键是运用性质找出对应点.
(3)旋转中心、旋转角、旋转方向不同,得到
的同一图形的旋转图形的位置不同,但都全等.自主探究4.性质的应用例 如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.巩固练习(1)教材第59页练习2.(2)教材第61页练习第1、2题.(3)教材第62页练习.巩固练习补充练习:
已知:△ABC以C为旋转中心,画出逆时
针旋转90°后的旋转图形.总结提高(1)旋转定义.1.小结(2)旋转性质.(3)旋转作图.2.布置作业
(1)教材第62页习题23.1第4题(必做).
(2)教材第62页习题23.1第1题(选做).
(3)教材第63页习题23.1第5、6、7题.
(4)教材第63页习题23.1第8、9题.总结提高谢谢 !
同课章节目录
