2017年秋人教版九年级上册数学课件23.2.2中心对称图形 课件
文档属性
| 名称 | 2017年秋人教版九年级上册数学课件23.2.2中心对称图形 课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 912.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-02 17:10:21 | ||
图片预览




文档简介
(共19张PPT)
第二十三章 旋转
23.2 中心对称
第2课时 中心对称图形
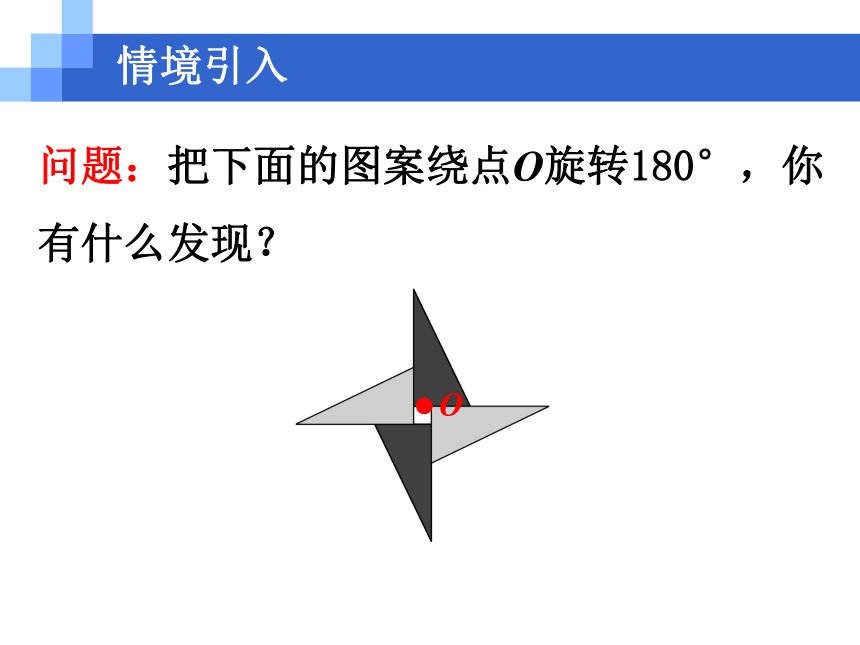
问题:把下面的图案绕点O旋转180°,你有什么发现?
情境引入
.
O
问题:把下面的图案绕点O 旋转180°,你有什么发现
情境引入
.
O
问题:把下面的图案绕点O旋转180°,你有什么发现?
情境引入
.
O
自主探究
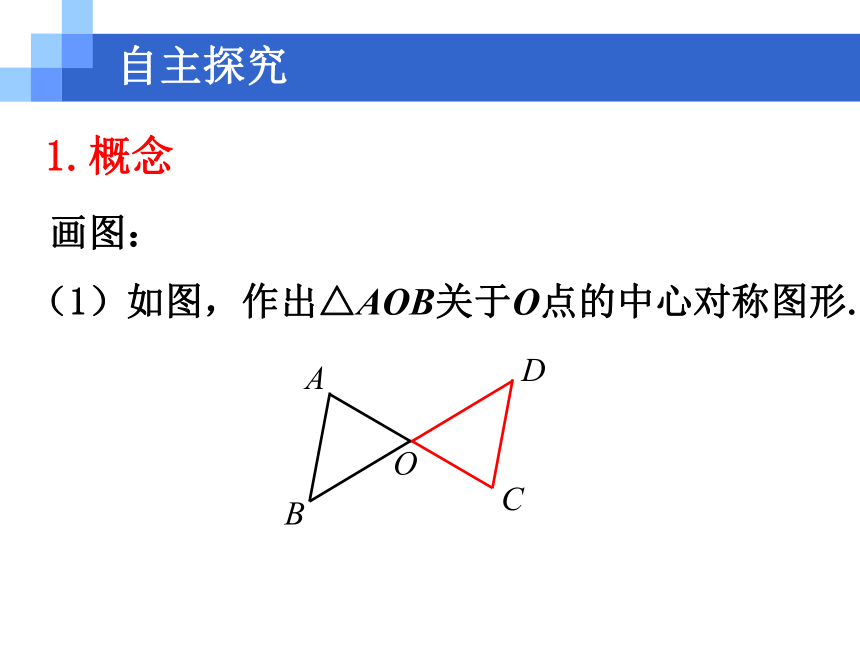
1.概念
画图:
(1)如图,作出△AOB关于O点的中心对称图形.
D
C
O
A
B
自主探究
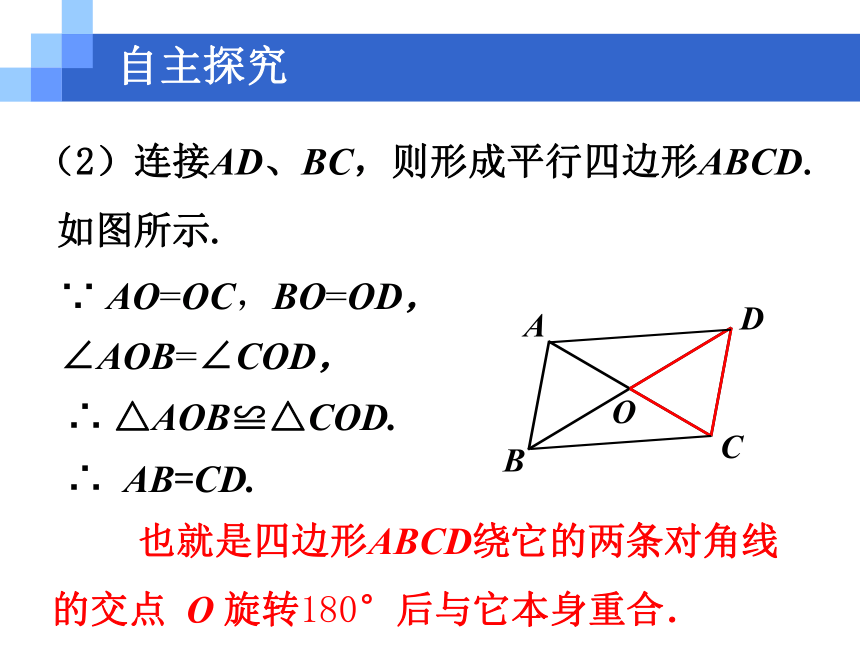
(2)连接AD、BC,则形成平行四边形ABCD.
如图所示.
∵ AO=OC,BO=OD,
∠AOB=∠COD,
∴ △AOB≌△COD.
∴ AB=CD.
也就是四边形ABCD绕它的两条对角线的交点 O 旋转180°后与它本身重合.
A
B
D
C
O
自主探究
像这样,把一个图形绕着某一个点旋转 180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
A
B
B
D
O
O
线段、平行四边形都是中心对称图形.
A
C
自主探究
三角形、梯形、正五边形都不是中心对称图形.
自主探究
自主探究
2.概念理解
(2)你能说出中心对称和中心对称图形的区别吗?
(1)举例:举现实生活中的中心对称图形的
例子,并指出对称中心.
自主探究
名称 中心对称 中心对称图形
定义 把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称.这个点叫做对称中心.这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点. 把一个图形绕某一个点旋转 180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
性质 ①两个图形完全重合.
②对应点连线都经过对称中心,并且被对称中心平分.
自主探究
名称 中心对称 中心对称图形
区别
①两个图形的关系.
②对称点在两个图形上
①具有某种性质的一个图形.
②对称点在一个图形上.
联系 若把中心对称图形的两部分分别看作两个图形,则
它们成中心对称;若把中心对称的两个图形看作一个整
体,则成为中心对称图形.
巩固练习
教材第67页练习第1、2题.
巩固练习
1.在26个英文大写正体字母中,哪些字母是中心
对称图形?
A B C D E F G H
I J K L M N O P Q
R S T U V W X Y Z
补充练习:
2.从一副扑克牌中抽出如下四张牌,其中是中 心对称图形的有( )
A
A.1 张 B.2 张 C.3 张 D.4 张
巩固练习
3.判断下列图形是否为中心对称图形.
×
√
√
√
√
巩固练习
巩固练习
4. 判断下列说法是否正确.
(1)轴对称图形也是中心对称图形. ( )
(2)旋转对称图形也是中心对称图形. ( )
(3)平行四边形、长方形和正方形都是中心对称
图形,对角线的交点是它们的对称中心. ( )
(4)角是轴对称图形也是中心对称图形. ( )
√
×
×
×
总结提高
(1)中心对称图形,对称中心.
1.小结
(2)方法规律总结:中心对称图形的性质.
(3)中心对称和中心对称图形的区别与联系.
(4)中心对称图形和轴对称图形的区别与联系.
2.布置作业
习题23.2第2题.
第二十三章 旋转
23.2 中心对称
第2课时 中心对称图形
问题:把下面的图案绕点O旋转180°,你有什么发现?
情境引入
.
O
问题:把下面的图案绕点O 旋转180°,你有什么发现
情境引入
.
O
问题:把下面的图案绕点O旋转180°,你有什么发现?
情境引入
.
O
自主探究
1.概念
画图:
(1)如图,作出△AOB关于O点的中心对称图形.
D
C
O
A
B
自主探究
(2)连接AD、BC,则形成平行四边形ABCD.
如图所示.
∵ AO=OC,BO=OD,
∠AOB=∠COD,
∴ △AOB≌△COD.
∴ AB=CD.
也就是四边形ABCD绕它的两条对角线的交点 O 旋转180°后与它本身重合.
A
B
D
C
O
自主探究
像这样,把一个图形绕着某一个点旋转 180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
A
B
B
D
O
O
线段、平行四边形都是中心对称图形.
A
C
自主探究
三角形、梯形、正五边形都不是中心对称图形.
自主探究
自主探究
2.概念理解
(2)你能说出中心对称和中心对称图形的区别吗?
(1)举例:举现实生活中的中心对称图形的
例子,并指出对称中心.
自主探究
名称 中心对称 中心对称图形
定义 把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称.这个点叫做对称中心.这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点. 把一个图形绕某一个点旋转 180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
性质 ①两个图形完全重合.
②对应点连线都经过对称中心,并且被对称中心平分.
自主探究
名称 中心对称 中心对称图形
区别
①两个图形的关系.
②对称点在两个图形上
①具有某种性质的一个图形.
②对称点在一个图形上.
联系 若把中心对称图形的两部分分别看作两个图形,则
它们成中心对称;若把中心对称的两个图形看作一个整
体,则成为中心对称图形.
巩固练习
教材第67页练习第1、2题.
巩固练习
1.在26个英文大写正体字母中,哪些字母是中心
对称图形?
A B C D E F G H
I J K L M N O P Q
R S T U V W X Y Z
补充练习:
2.从一副扑克牌中抽出如下四张牌,其中是中 心对称图形的有( )
A
A.1 张 B.2 张 C.3 张 D.4 张
巩固练习
3.判断下列图形是否为中心对称图形.
×
√
√
√
√
巩固练习
巩固练习
4. 判断下列说法是否正确.
(1)轴对称图形也是中心对称图形. ( )
(2)旋转对称图形也是中心对称图形. ( )
(3)平行四边形、长方形和正方形都是中心对称
图形,对角线的交点是它们的对称中心. ( )
(4)角是轴对称图形也是中心对称图形. ( )
√
×
×
×
总结提高
(1)中心对称图形,对称中心.
1.小结
(2)方法规律总结:中心对称图形的性质.
(3)中心对称和中心对称图形的区别与联系.
(4)中心对称图形和轴对称图形的区别与联系.
2.布置作业
习题23.2第2题.
同课章节目录
