人教版数学七年级上册课件第1章有理数1.2.2 数轴 课件
文档属性
| 名称 | 人教版数学七年级上册课件第1章有理数1.2.2 数轴 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 422.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-02 17:36:40 | ||
图片预览






文档简介
课件14张PPT。 第一章 有理数
1.2 有理数
1.2.2 数轴读一读 你能读出下列温度计的度数吗?小组探究 在一条东西向的马路上,有一个汽车站牌,汽车站牌东3 m和7.5 m处分别有一棵柳树和一棵杨树,汽车站牌西3 m和4.8 m处分别有一棵槐树和一根电线杆,你能画图表示这一情境吗?小组讨论一下!议一议 1.小组讨论问题:
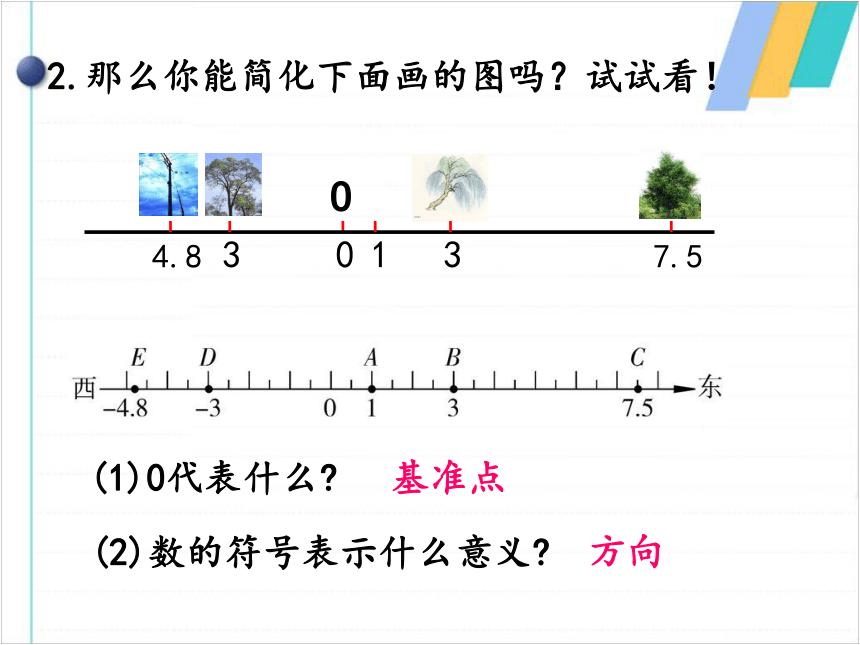
(1)马路可以用什么几何图形代表?基准点直线方向,与站牌的距离(2)你认为站牌起什么作用?(3)你是怎样确定问题中各物体的位置的? 2.那么你能简化下面画的图吗?试试看! ? (1)0代表什么?基准点 (2)数的符号表示什么意义?方向 由上述的思考探究过程你有什么启发?
你能用一条直线表示有理数吗?需要哪些条件呢?数轴的三要素:原点、正方向、单位长度. 准备一根绳子,请8个同学走上来,把位置调整为等距离,规定第3个同学为原点,由西向东为正方向,每个同学都有一个整数编号,请大家记住,现在请第一排的同学依次发出口令,口令为数字时,该数对应的同学要回答“到”;口令为该同学的名字时,该同学要报出他对应的“数字”,如果规定第4个同学为原点,游戏还能进行吗?一起来玩游戏1.你能举出一些在现实生活中用直线表示数的实际例子吗?
2.如果给你一些数,你能相应地在数轴上找到它们的准确位置吗?如果给你数轴上的点,你能读出它所表示的数吗?
3.哪些数表示的点在原点的左边,哪些数表示的点在原点的右边,由此你会发现什么规律?
想一想4.每个数表示的点到原点的距离是多少?由此你会发现什么规律?想一想归纳 一般地,设a是一个正数,则数轴上表示数a的点在原点的 边,与原点的距离是 个单位长度;表示数-a的点在原点
的 边,与原点的距离是 个单位长度.右a左a随堂练习1.如图,写出数轴上点A,B,C,D,E 表示的数. -3 -2-10 1 23 EBACD﹒.....E( -3 ),B( -2 ), A( 0 ) , C( 1 ),D( 2.5 ).?3.数轴上,如果表示a的点在原点的左边,那么a是一个( )数;如果表示数b的
点在原点的右边,那么b是一个( )数. 负正布置作业习题1.2第2题.
1.2 有理数
1.2.2 数轴读一读 你能读出下列温度计的度数吗?小组探究 在一条东西向的马路上,有一个汽车站牌,汽车站牌东3 m和7.5 m处分别有一棵柳树和一棵杨树,汽车站牌西3 m和4.8 m处分别有一棵槐树和一根电线杆,你能画图表示这一情境吗?小组讨论一下!议一议 1.小组讨论问题:
(1)马路可以用什么几何图形代表?基准点直线方向,与站牌的距离(2)你认为站牌起什么作用?(3)你是怎样确定问题中各物体的位置的? 2.那么你能简化下面画的图吗?试试看! ? (1)0代表什么?基准点 (2)数的符号表示什么意义?方向 由上述的思考探究过程你有什么启发?
你能用一条直线表示有理数吗?需要哪些条件呢?数轴的三要素:原点、正方向、单位长度. 准备一根绳子,请8个同学走上来,把位置调整为等距离,规定第3个同学为原点,由西向东为正方向,每个同学都有一个整数编号,请大家记住,现在请第一排的同学依次发出口令,口令为数字时,该数对应的同学要回答“到”;口令为该同学的名字时,该同学要报出他对应的“数字”,如果规定第4个同学为原点,游戏还能进行吗?一起来玩游戏1.你能举出一些在现实生活中用直线表示数的实际例子吗?
2.如果给你一些数,你能相应地在数轴上找到它们的准确位置吗?如果给你数轴上的点,你能读出它所表示的数吗?
3.哪些数表示的点在原点的左边,哪些数表示的点在原点的右边,由此你会发现什么规律?
想一想4.每个数表示的点到原点的距离是多少?由此你会发现什么规律?想一想归纳 一般地,设a是一个正数,则数轴上表示数a的点在原点的 边,与原点的距离是 个单位长度;表示数-a的点在原点
的 边,与原点的距离是 个单位长度.右a左a随堂练习1.如图,写出数轴上点A,B,C,D,E 表示的数. -3 -2-10 1 23 EBACD﹒.....E( -3 ),B( -2 ), A( 0 ) , C( 1 ),D( 2.5 ).?3.数轴上,如果表示a的点在原点的左边,那么a是一个( )数;如果表示数b的
点在原点的右边,那么b是一个( )数. 负正布置作业习题1.2第2题.
