4.4课题学习 设计制作长方体形状的包装纸盒 课件
文档属性
| 名称 | 4.4课题学习 设计制作长方体形状的包装纸盒 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-03 10:33:28 | ||
图片预览





文档简介
课件22张PPT。4.4 展开与折叠能根据展开图判断几何体的形状; 能画出简单的几何体的展开图; 能做一个长方体的纸盒。 这些精美的包装盒是怎么制成的? 要设计、制作一个包装盒,除了美术设计以外,还要了解它展开后的形状,好根据它来准备材料,这就是我们今天学习的立体图形的展开图.
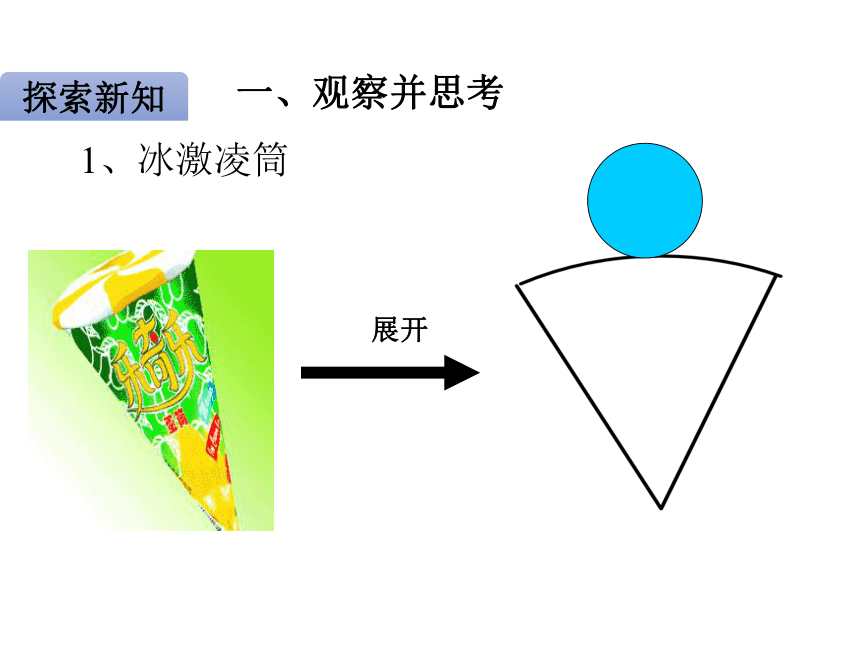
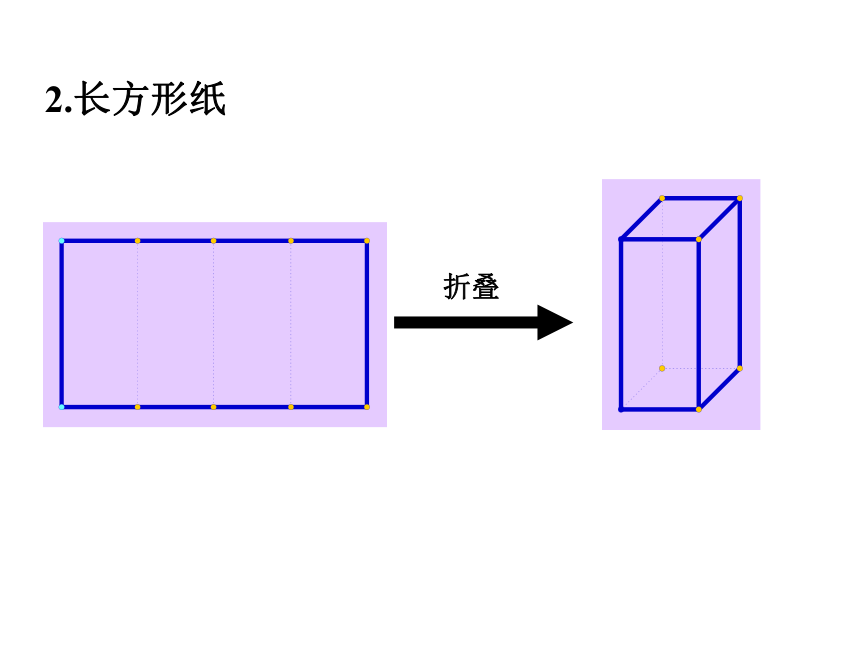
复习导入 有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展成平面图形.这样的平面图形称为相应立体图形的展开图.一、观察并思考1、冰激凌筒探索新知2.长方形纸交流归纳:有些立体图形平面图形有些平面图形立体图形二.操作实践,感知图形,
能根据展开图判断立体图形;
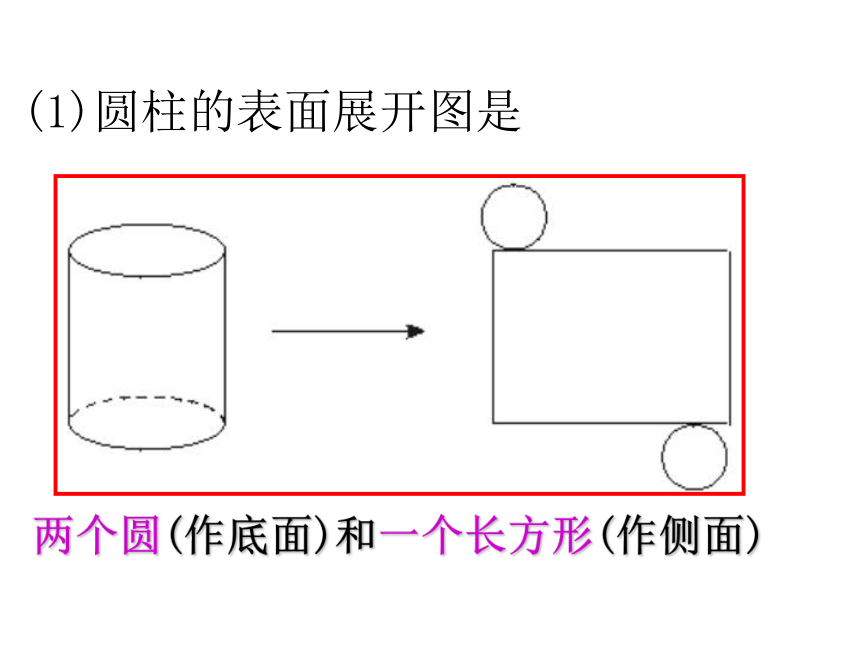
能判断平面图形是否为立体图形的展开图。几种常见几何图形的展开与折叠举例讲解(1)圆柱的表面展开图是两个圆(作底面)和一个长方形(作侧面) (2)圆锥的表面展开图是一个圆(作底面)和一个扇形(作侧面) 3、棱柱的表面展开图是两个完全相同的多边形(作底面)和
几个长方形(作侧面)
注意:棱柱的两个底面分别在侧面展开图的两端。棱锥的展开图是由一个多边形(作底)和几个三角形(作侧面)组成的
底面图形的边数=侧面三角形的个数[例]下面图形经过折叠能否围成棱柱?(3)可以折成棱柱 .(1)侧面数(4个)≠底面边数(3条),不能围成棱柱.(2)两底面在侧面展开图的同一端,不在两端,所以也不能围成棱柱.典题精讲想一想:下列图形都是正方体的展开图吗?(5)(2)(6)(3)(1)(4)(√)(√)(√)(×)(×)(√)四个面连成一排的三个面连成一排的两个面连成一排的正方体的展开图(演示)棒1、如果“你”在前面,那么谁在后面?思考2、“坚”在下,“就”在后,胜利在哪里? “胜”在上,
“利”在前!A.圆柱、六棱柱、圆锥、三棱柱B.圆柱、六棱柱、圆锥、三棱锥C.圆锥、六棱柱、圆柱、三棱柱D.圆锥、六棱柱、圆柱、三棱锥下面展开图依次表示的物体是下边的平面图形不是上面长方体展开图的是 ( )(A)(B)(C)(D)D1、立体图形是由平面图形组成的。
2、能根据展开图判断立体图形。
3、能判断平面图形是否为立体图形的展开图。1、制作精美的盒子做为给父母、老师或朋友的元旦礼物。
2、制作正方体的11种展开图片并折叠成正方体
3 、p149 10小题作业课堂小结将相对的两个面涂上相同的颜色,正方体的平面展开图共有以下11种: 如图,左边的图形可能是右边哪个图形的展开图?(D)(C)
复习导入 有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展成平面图形.这样的平面图形称为相应立体图形的展开图.一、观察并思考1、冰激凌筒探索新知2.长方形纸交流归纳:有些立体图形平面图形有些平面图形立体图形二.操作实践,感知图形,
能根据展开图判断立体图形;
能判断平面图形是否为立体图形的展开图。几种常见几何图形的展开与折叠举例讲解(1)圆柱的表面展开图是两个圆(作底面)和一个长方形(作侧面) (2)圆锥的表面展开图是一个圆(作底面)和一个扇形(作侧面) 3、棱柱的表面展开图是两个完全相同的多边形(作底面)和
几个长方形(作侧面)
注意:棱柱的两个底面分别在侧面展开图的两端。棱锥的展开图是由一个多边形(作底)和几个三角形(作侧面)组成的
底面图形的边数=侧面三角形的个数[例]下面图形经过折叠能否围成棱柱?(3)可以折成棱柱 .(1)侧面数(4个)≠底面边数(3条),不能围成棱柱.(2)两底面在侧面展开图的同一端,不在两端,所以也不能围成棱柱.典题精讲想一想:下列图形都是正方体的展开图吗?(5)(2)(6)(3)(1)(4)(√)(√)(√)(×)(×)(√)四个面连成一排的三个面连成一排的两个面连成一排的正方体的展开图(演示)棒1、如果“你”在前面,那么谁在后面?思考2、“坚”在下,“就”在后,胜利在哪里? “胜”在上,
“利”在前!A.圆柱、六棱柱、圆锥、三棱柱B.圆柱、六棱柱、圆锥、三棱锥C.圆锥、六棱柱、圆柱、三棱柱D.圆锥、六棱柱、圆柱、三棱锥下面展开图依次表示的物体是下边的平面图形不是上面长方体展开图的是 ( )(A)(B)(C)(D)D1、立体图形是由平面图形组成的。
2、能根据展开图判断立体图形。
3、能判断平面图形是否为立体图形的展开图。1、制作精美的盒子做为给父母、老师或朋友的元旦礼物。
2、制作正方体的11种展开图片并折叠成正方体
3 、p149 10小题作业课堂小结将相对的两个面涂上相同的颜色,正方体的平面展开图共有以下11种: 如图,左边的图形可能是右边哪个图形的展开图?(D)(C)
