2.2整式的加减---整式加减的应用课件
文档属性
| 名称 | 2.2整式的加减---整式加减的应用课件 |  | |
| 格式 | zip | ||
| 文件大小 | 614.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-03 11:18:23 | ||
图片预览








文档简介
课件20张PPT。整式的加减(三)整式加减的应用能运用整式的加减进行实际应用; 灵活地进行整式的加减; 会列式进行整式的加减运算。 复习导入1.复习同类项及合并同类项法则;2.复习去括号法则。 1.整式加减运算的最后结果也是一个整式,一般地,要求这个结果是最简的. 回顾 & 思考2. 一个最简的整式中不应再有同类项 因此,整式加减运算的过程与步骤,包含以下两个运算:去括号、合并同类项例3:一种笔记本的单价是x元,圆珠笔的单价是y元。小红买这种笔记本3个,买圆珠笔2支;小明买这种笔记本4个,买圆珠笔3支。买这些笔记本和圆珠笔,小红和小明一共花了多少钱?解法二:小红和小明买笔记本共花 费(3x+4x)元,买圆珠笔共花费(2y+3y)元.
小明和小红一共花 费 (3x+4x)+ (2y+3y)
=7x+5y (元)解法一:小红买笔记本和圆珠笔共花费(3x+2y)元,小明买笔记本和圆珠笔共花费(4x+3y)元.
小明和小红一共花费(3x+2y)+ (4x+3y)
=3x+2y+4x+3y
=7x+5 y (元)
探索新知例4 做大小两个长方体纸盒,尺寸如下(单位:cm):(1)做这两个纸盒共用料多少平方厘米?
(2)做大纸盒比做小纸盒多用料多少平方厘米? 例5: 小明家的收入分农业收入和其他收 入两部分,今年其他收入是农业收入的2倍,预计明年农业收入将减少15%,而其他收入将增加35%,那么预计小明家明年的总收入是增加,还是减少?典题精讲 解:设小明家今年农业收入为a元.
则今年的全年收入为:a+2a=3a(元).
明年的农业收入为:(1-15%)a (元);
明年的其他收入为:2(1+ 35%)×a(元);
所以明年的全年收入为:
(1-15%)a+ 2(1+ 35%)×a
=a-0.15a+2a+0.7a
=3.55a(元).
因为3a< 3.55a
所以小明家明年的收入将增加.
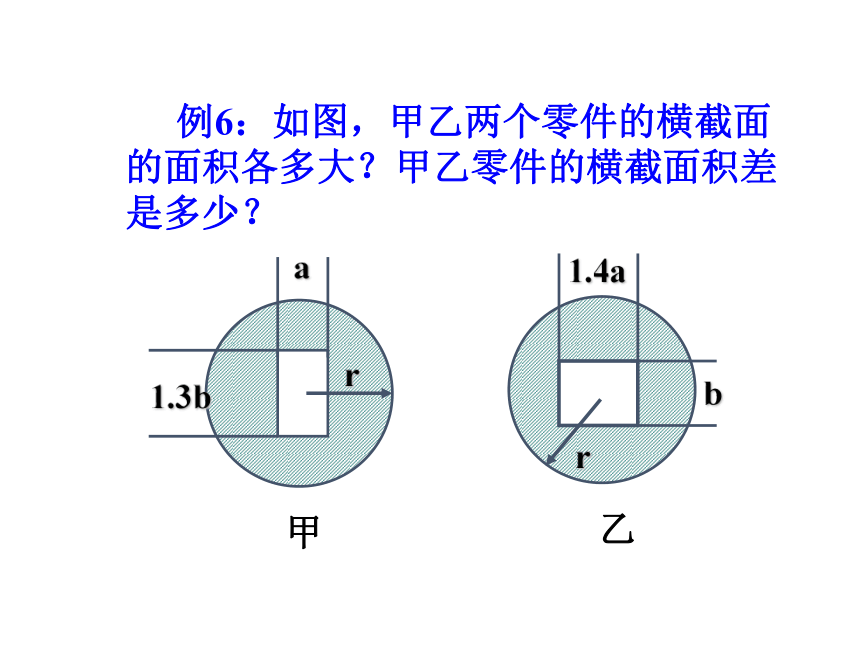
答:小明家明年的收入将增加. 例6:如图,甲乙两个零件的横截面的面积各多大?甲乙零件的横截面积差是多少?甲乙解:甲零件的横截面积为:πr2-1.3b×a= πr2-1.3ab.
乙零件的横截面积为:
πr2-1.4a×b= πr2-1.4ab.
因为πr2-1.3ab< πr2-1.4ab
所以甲零件的横截面积大.
甲乙两零件的横截面积差为:
(πr2-1.3ab)-( πr2-1.4ab)
=πr2-1.3ab -πr2+1.4ab
=0.1ab. (1)用棋子摆成下面的“小屋子”:摆第 1 个“小屋子”需要 5 枚 棋子;摆第 2 个“小屋子”需要 枚 棋子;摆第 3 个“小屋子”需要 枚 棋子.1117思考用棋子摆成下面的“小屋子”:(1)摆第 10 个这样的“小屋子”需要 枚 棋子,(2)摆第 n 个这样的“小屋子”需要 枚 棋子.23595+6(n-1)知识拓展1.同类项、合并同类项的概念.
2.合并同类项法则.
3.去括号法则.
4. 实际问题中整式的加减应用,要认真分析题意,正确列出算式.课堂小结 (4) 一个多项式加上2x2-x3-5-3x4得3x4-5x3-3,求这个多项式.解:由题意得:
(3x4-5x3-3) -(2x2-x3-5-3x4)
= 3x4-5x3-3 -2x2+x3+5+3x4
=(3-2)x4+(-5+1)x3-2x2+(-3+5)
=x4-4x3-2x2+2.
答:这个多项式是x4-4x3-2x2+2.课后思考 (5) 已知A+B=-2x2-4x+3,A-C=3x-4x2-9,当x=2时,求B+C的值.解:由题意得:
B= -2x2-4x+3-A;
C=A-(3x-4x2-9).
所以
B+C= (-2x2-4x+3-A)+ [A-(3x-4x2-9)] = -2x2-4x+3-A+ A-3x+4x2+9
=(-2+4)x2+(-4-3)x+(-A+ A) +12
=2x2-7x+12
当x=2时,B+C=2×2×2-7×2+12=6. (6).一种长方形餐桌的四周可坐6人用餐,现把n张这样的餐桌按如图方式拼接起来,问四周可坐多少人用餐?若用餐的人数有22人,则这样的餐桌需要多少张?解:1张这样的餐桌可以坐6人;
2张这样的餐桌可以坐10人;
3张这样的餐桌可以坐14人;
···
n张这样的餐桌可以坐(4n+2)人.
若用餐人数为22人,
则4n+2=22,
得:n=5.
答: n张这样的餐桌可以坐(4n+2)人,若用餐的人数有22人,则这样的餐桌需要5张. 练习:P70 1、2作业:P71 3、6、8
小明和小红一共花 费 (3x+4x)+ (2y+3y)
=7x+5y (元)解法一:小红买笔记本和圆珠笔共花费(3x+2y)元,小明买笔记本和圆珠笔共花费(4x+3y)元.
小明和小红一共花费(3x+2y)+ (4x+3y)
=3x+2y+4x+3y
=7x+5 y (元)
探索新知例4 做大小两个长方体纸盒,尺寸如下(单位:cm):(1)做这两个纸盒共用料多少平方厘米?
(2)做大纸盒比做小纸盒多用料多少平方厘米? 例5: 小明家的收入分农业收入和其他收 入两部分,今年其他收入是农业收入的2倍,预计明年农业收入将减少15%,而其他收入将增加35%,那么预计小明家明年的总收入是增加,还是减少?典题精讲 解:设小明家今年农业收入为a元.
则今年的全年收入为:a+2a=3a(元).
明年的农业收入为:(1-15%)a (元);
明年的其他收入为:2(1+ 35%)×a(元);
所以明年的全年收入为:
(1-15%)a+ 2(1+ 35%)×a
=a-0.15a+2a+0.7a
=3.55a(元).
因为3a< 3.55a
所以小明家明年的收入将增加.
答:小明家明年的收入将增加. 例6:如图,甲乙两个零件的横截面的面积各多大?甲乙零件的横截面积差是多少?甲乙解:甲零件的横截面积为:πr2-1.3b×a= πr2-1.3ab.
乙零件的横截面积为:
πr2-1.4a×b= πr2-1.4ab.
因为πr2-1.3ab< πr2-1.4ab
所以甲零件的横截面积大.
甲乙两零件的横截面积差为:
(πr2-1.3ab)-( πr2-1.4ab)
=πr2-1.3ab -πr2+1.4ab
=0.1ab. (1)用棋子摆成下面的“小屋子”:摆第 1 个“小屋子”需要 5 枚 棋子;摆第 2 个“小屋子”需要 枚 棋子;摆第 3 个“小屋子”需要 枚 棋子.1117思考用棋子摆成下面的“小屋子”:(1)摆第 10 个这样的“小屋子”需要 枚 棋子,(2)摆第 n 个这样的“小屋子”需要 枚 棋子.23595+6(n-1)知识拓展1.同类项、合并同类项的概念.
2.合并同类项法则.
3.去括号法则.
4. 实际问题中整式的加减应用,要认真分析题意,正确列出算式.课堂小结 (4) 一个多项式加上2x2-x3-5-3x4得3x4-5x3-3,求这个多项式.解:由题意得:
(3x4-5x3-3) -(2x2-x3-5-3x4)
= 3x4-5x3-3 -2x2+x3+5+3x4
=(3-2)x4+(-5+1)x3-2x2+(-3+5)
=x4-4x3-2x2+2.
答:这个多项式是x4-4x3-2x2+2.课后思考 (5) 已知A+B=-2x2-4x+3,A-C=3x-4x2-9,当x=2时,求B+C的值.解:由题意得:
B= -2x2-4x+3-A;
C=A-(3x-4x2-9).
所以
B+C= (-2x2-4x+3-A)+ [A-(3x-4x2-9)] = -2x2-4x+3-A+ A-3x+4x2+9
=(-2+4)x2+(-4-3)x+(-A+ A) +12
=2x2-7x+12
当x=2时,B+C=2×2×2-7×2+12=6. (6).一种长方形餐桌的四周可坐6人用餐,现把n张这样的餐桌按如图方式拼接起来,问四周可坐多少人用餐?若用餐的人数有22人,则这样的餐桌需要多少张?解:1张这样的餐桌可以坐6人;
2张这样的餐桌可以坐10人;
3张这样的餐桌可以坐14人;
···
n张这样的餐桌可以坐(4n+2)人.
若用餐人数为22人,
则4n+2=22,
得:n=5.
答: n张这样的餐桌可以坐(4n+2)人,若用餐的人数有22人,则这样的餐桌需要5张. 练习:P70 1、2作业:P71 3、6、8
