1.2.4 绝对值 课件
图片预览






文档简介
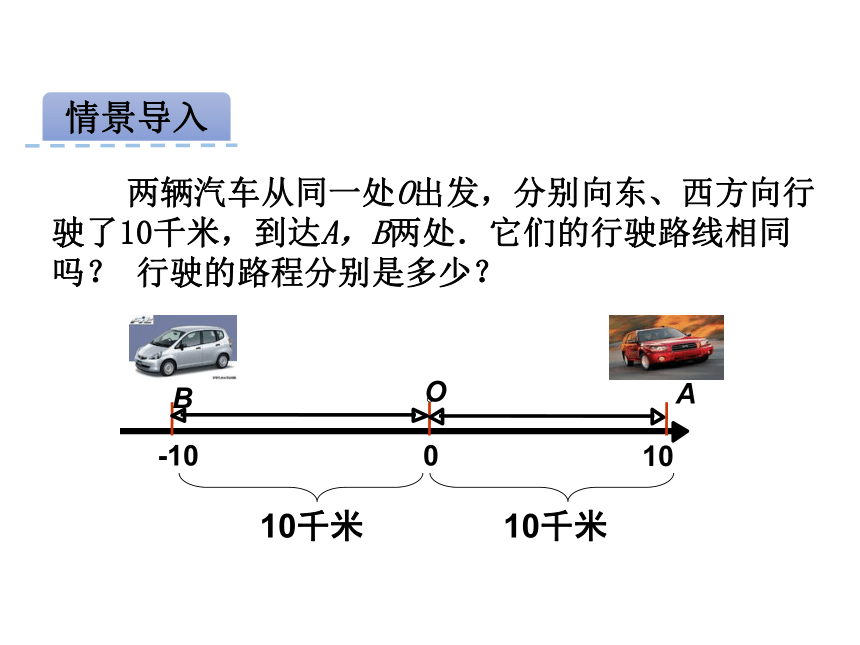
课件23张PPT。1.2.4 绝对值会求一个数的绝对值,会求绝对值已知的数;理解绝对值的概念及其几何意义,体会绝对值的作用; 掌握有理数比较大小的法则. 两辆汽车从同一处O出发,分别向东、西方向行
驶了10千米,到达A,B两处.它们的行驶路线相同
吗? 行驶的路程分别是多少?
10千米10千米
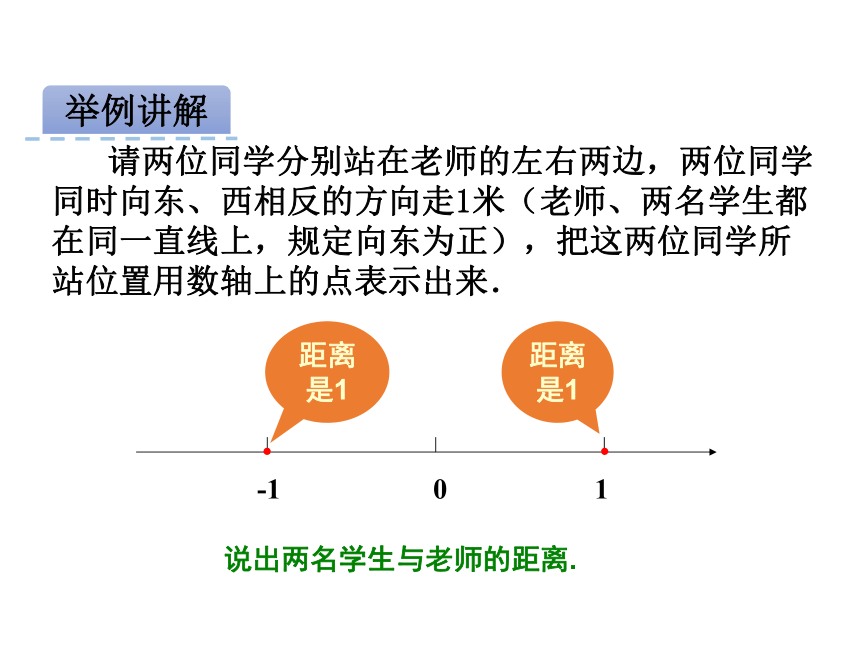
请两位同学分别站在老师的左右两边,两位同学
同时向东、西相反的方向走1米(老师、两名学生都
在同一直线上,规定向东为正),把这两位同学所
站位置用数轴上的点表示出来.
说出两名学生与老师的距离.距离是1距离是1
一般地,数轴上表示数 的点与原点的距离
叫做数 的绝对值,记作| | .
例如,上面的问题中,在数轴上表示数-1的点
和表示数1的点与原点的距离都是1,所以,1与-1
的绝对值都是1,即|1|=1,|-1|=1. 绝对值概念:1:-2的绝对值表示它离原点的距离是 个单位,
记作 .
2:-0.8的绝对值是 .
3:口答:
(1)|+6|=?????? ,| |=?????? , |8.2|=??????;
(2)|0|=?????? ;
(3)|-3|=?????? ,|- |=?????? , |-0.6|=???? . 268.2030.6 0.8
数 的绝对值的一般规律:
3.0的绝对值是0.即:①若 >0,则| |= ;
②若 <0,则| |=– ;
③若 =0,则| |=0.
2.一个负数的绝对值是它的相反数; 1.一个正数的绝对值是它本身; 1.有没有绝对值等于-2的数?一个数的绝对值会是
负数吗?为什么?不论有理数 取何值,它的绝对值
总是什么数? 不论有理数 取何值,它的绝对值总是正数或0,
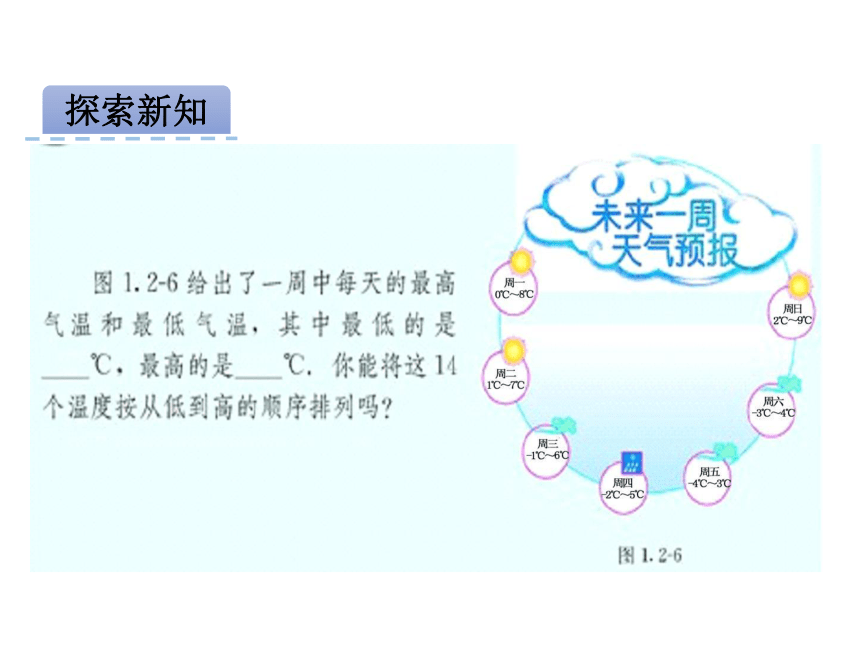
即对任意有理数 ,总有 ≥0. 你能把14个气温从低到高排列吗?能把这14个数
用数轴上的点表示出来吗?观察这些点在数轴上的位
置,思考它们与温度的高低之间的关系,你觉得两个
有理数可以比较大小吗? 数轴上的两个点,右边的点表示的数与左边的点表示的数的大小关系是怎样的?0123-1-2-3在数轴上表示有理数,左边的数小于右边的数.负数小于0,正数大于负数. 正数大于0,越来越大两个负数,绝对值大的反而小.互为相反数的两个数的绝对值有什么关系? 虽然一对相反数分别在原点两边,但它们
到原点的距离是相等的.所以互为相反数的两
个数的绝对值相等.1.说出下列各式的值:
2.求下列各数的绝对值:
6 , -6 , -3.9 , +3.9, , , 0.1、化简:
0-3.98.6-4-10.73-4.53.75+(-2.5)- -0.6-(- )教师将写有数字的卡片分给几名学生,拿到卡片
的学生按所拿卡片上数字的大小,由小到大排队.
1、如果 ,
那么 a=_____,b=_____. 2、已知x=30,y=-4,
则判断下列说法是否正确:
(1)有理数的绝对值一定是正数;
(2)如果两个数的绝对值相等,那么这两个数相等;
(3)符号相反且绝对值相等的数互为相反数;
(4)一个数的绝对值越大,表示它的点在数轴上越靠右;
(5)一个数的绝对值越大,表示它的点在数轴上离原点越远.1、一个数的绝对值是7,求这个数.2、满足︱x︱≤3的所有整数是 ;3、绝对值大于2并且不大于5的负整数有 .判断并改错:
(1)一个数的绝对值等于本身,则这个数一定是正数 .( )
(2)一个数的绝对值等于它的相反数,这个数一定是负数.( )
(3)如果两个数的绝对值相等,那么这两个数一定相等( )
(4)如果两个数不相等,那么这两个数的绝对值一定不等.( )
(5)有理数的绝对值一定是非负数. ( )
(6)有理数没有最小的,有理数的绝对值也没有最小的.( )
(7)两个有理数,绝对值大的反而小. ( )
(8)两个有理数为a 、b,若a >b,则|a|>|b|. ( )1.一个正数的绝对值是它本身;一个负数的绝对值是它的相反数; 0的绝对值是0 . 2.若a为有理数,则|a|≥0. 3.零作为一个特殊的数,有其特殊的属性:
①是绝对值最小的数;②相反数是它本身;③绝对值是它本身.4.比较有理数大小的方法.
方法①:数轴上表示的两个数,右边的总比左边的大.
方法②:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小. 解:则由图2可知-a >2>b>0>-b>-2>a.图1由相反数的意义,在数轴上画出表示-a,-b的点,如图2所示,图2课后思考有理数a,b在数轴上的位置对应如图1,
试用“>”将a,b,-a,-b,0,2,2连接起来.
驶了10千米,到达A,B两处.它们的行驶路线相同
吗? 行驶的路程分别是多少?
10千米10千米
请两位同学分别站在老师的左右两边,两位同学
同时向东、西相反的方向走1米(老师、两名学生都
在同一直线上,规定向东为正),把这两位同学所
站位置用数轴上的点表示出来.
说出两名学生与老师的距离.距离是1距离是1
一般地,数轴上表示数 的点与原点的距离
叫做数 的绝对值,记作| | .
例如,上面的问题中,在数轴上表示数-1的点
和表示数1的点与原点的距离都是1,所以,1与-1
的绝对值都是1,即|1|=1,|-1|=1. 绝对值概念:1:-2的绝对值表示它离原点的距离是 个单位,
记作 .
2:-0.8的绝对值是 .
3:口答:
(1)|+6|=?????? ,| |=?????? , |8.2|=??????;
(2)|0|=?????? ;
(3)|-3|=?????? ,|- |=?????? , |-0.6|=???? . 268.2030.6 0.8
数 的绝对值的一般规律:
3.0的绝对值是0.即:①若 >0,则| |= ;
②若 <0,则| |=– ;
③若 =0,则| |=0.
2.一个负数的绝对值是它的相反数; 1.一个正数的绝对值是它本身; 1.有没有绝对值等于-2的数?一个数的绝对值会是
负数吗?为什么?不论有理数 取何值,它的绝对值
总是什么数? 不论有理数 取何值,它的绝对值总是正数或0,
即对任意有理数 ,总有 ≥0. 你能把14个气温从低到高排列吗?能把这14个数
用数轴上的点表示出来吗?观察这些点在数轴上的位
置,思考它们与温度的高低之间的关系,你觉得两个
有理数可以比较大小吗? 数轴上的两个点,右边的点表示的数与左边的点表示的数的大小关系是怎样的?0123-1-2-3在数轴上表示有理数,左边的数小于右边的数.负数小于0,正数大于负数. 正数大于0,越来越大两个负数,绝对值大的反而小.互为相反数的两个数的绝对值有什么关系? 虽然一对相反数分别在原点两边,但它们
到原点的距离是相等的.所以互为相反数的两
个数的绝对值相等.1.说出下列各式的值:
2.求下列各数的绝对值:
6 , -6 , -3.9 , +3.9, , , 0.1、化简:
0-3.98.6-4-10.73-4.53.75+(-2.5)- -0.6-(- )教师将写有数字的卡片分给几名学生,拿到卡片
的学生按所拿卡片上数字的大小,由小到大排队.
1、如果 ,
那么 a=_____,b=_____. 2、已知x=30,y=-4,
则判断下列说法是否正确:
(1)有理数的绝对值一定是正数;
(2)如果两个数的绝对值相等,那么这两个数相等;
(3)符号相反且绝对值相等的数互为相反数;
(4)一个数的绝对值越大,表示它的点在数轴上越靠右;
(5)一个数的绝对值越大,表示它的点在数轴上离原点越远.1、一个数的绝对值是7,求这个数.2、满足︱x︱≤3的所有整数是 ;3、绝对值大于2并且不大于5的负整数有 .判断并改错:
(1)一个数的绝对值等于本身,则这个数一定是正数 .( )
(2)一个数的绝对值等于它的相反数,这个数一定是负数.( )
(3)如果两个数的绝对值相等,那么这两个数一定相等( )
(4)如果两个数不相等,那么这两个数的绝对值一定不等.( )
(5)有理数的绝对值一定是非负数. ( )
(6)有理数没有最小的,有理数的绝对值也没有最小的.( )
(7)两个有理数,绝对值大的反而小. ( )
(8)两个有理数为a 、b,若a >b,则|a|>|b|. ( )1.一个正数的绝对值是它本身;一个负数的绝对值是它的相反数; 0的绝对值是0 . 2.若a为有理数,则|a|≥0. 3.零作为一个特殊的数,有其特殊的属性:
①是绝对值最小的数;②相反数是它本身;③绝对值是它本身.4.比较有理数大小的方法.
方法①:数轴上表示的两个数,右边的总比左边的大.
方法②:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小. 解:则由图2可知-a >2>b>0>-b>-2>a.图1由相反数的意义,在数轴上画出表示-a,-b的点,如图2所示,图2课后思考有理数a,b在数轴上的位置对应如图1,
试用“>”将a,b,-a,-b,0,2,2连接起来.
