1.2.1 有理数 课件
图片预览






文档简介
课件24张PPT。1.2.1 有理数能根据不同的分类标准对有理数进行分类; 理解并掌握有理数的概念; 通过对有理数的分类,理解数学中的分类讨论思想. 复习导入上一节课我们讲了些什么内容?1,正数和负数.
2,0既不是正数,也不是负数.
3,正数与负数通常用来表示具有相反意义的
量.
4,“0”所表示的意思.
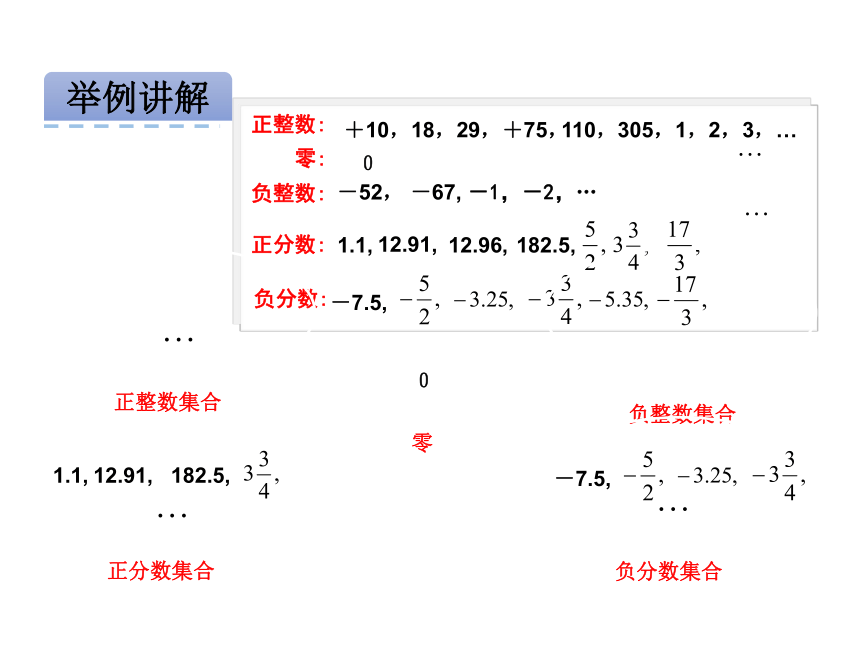
5,在生产中,通常用正负数来表示允许误差.举例讲解 女力士唐功红在女子+75公斤级举重比赛中,不负众望,以抓举122.5公斤,挺举182.5公斤,总成绩305公斤夺得第18枚金牌,与获银牌的韩国选手相比,她的抓举重量-7.5公斤,挺举重量+10公斤. 在女子柔道-52公斤级的冠军争夺战中,中国选手冼东妹仅用1.1分钟,就为中国柔道队夺得首枚金牌. 在男子110米栏决赛中,中国选手刘翔以12.91秒的成绩夺得金牌,这个成绩打破了12.96的奥运会纪录,平了世界纪录,实现了中国男子田径金牌0的突破.12.96, 182.5, 110,12.91,1.1,-520,+75,122.5,+10.-7.5,18,305,1.在以上各数中,哪些是在小学里学过的数?它们可以分为哪几类?2.在小学里学过的数中,有没有哪类数在上面没有出现?请举例说明.3.用计算器计算下列各分数的值,说明所有分数都可以化作什么数?4.由前面的结论,小学里学的数可以分为哪几类?零: 负分数:-52, -67, -1,-2,…0正整数:负整数:正整数集合正分数: +10,18,29,+75,12.96, -7.5,110,305,1,2,3,…182.5, 12.91,1.1,负整数集合举例讲解由刚才的演示可知:
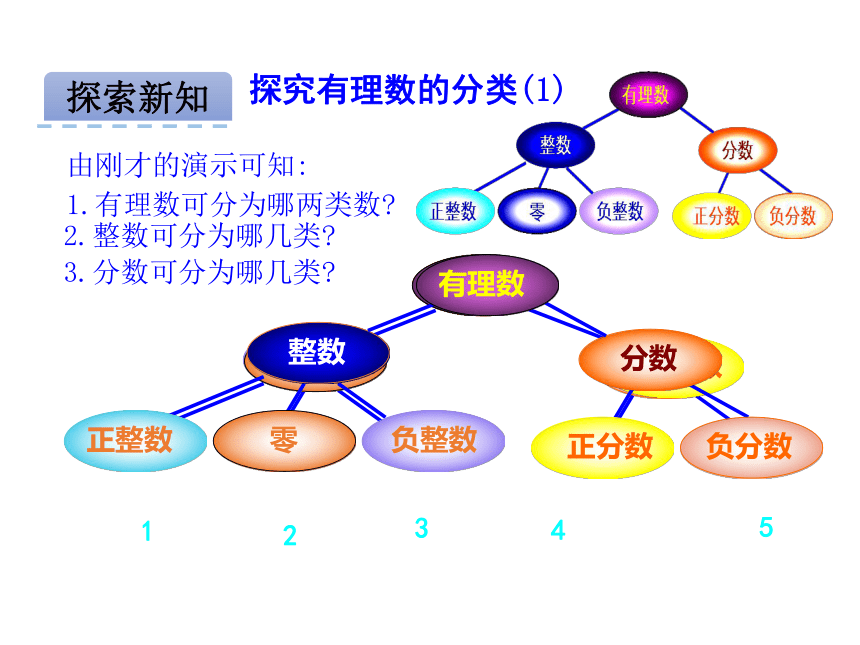
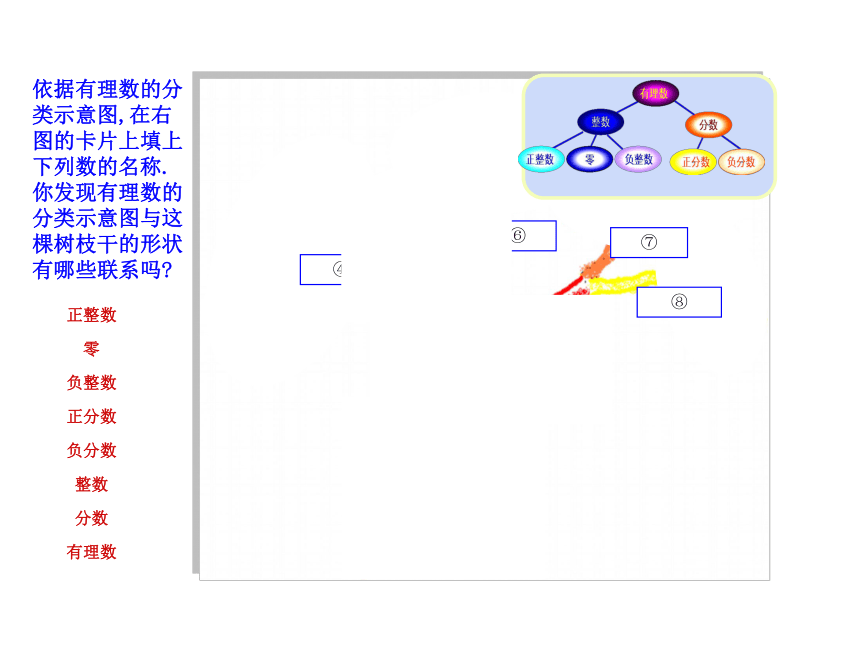
1.有理数可分为哪两类数?探究有理数的分类(1)2.整数可分为哪几类?3.分数可分为哪几类?12345探索新知⑧ ① ② ③ ④ ⑤ ⑥ ⑦ 依据有理数的分类示意图,在右图的卡片上填上下列数的名称.你发现有理数的分类示意图与这棵树枝干的形状有哪些联系吗?正整数零负整数正分数负分数整数分数有理数例1:把下列各数填在相应的集合中:正数集合:{ };
负数集合:{ };
分数集合:{ };
整数集合:{ };
非负数集合:{ };
有理数集合:{ };注意:1、像 这种可以先化简成整数的数是
整数不是分数;2、非负整数集合包括正整数和0,也称为自然数集合.1.在右边的有理数中,正整数有:__________;负分数有:_____________________________;整数有:_______________________________;分数有:_______________________________.探究有理数的分类(2) 小组讨论,合作完成讨论题,集中交流,形成正确分类方法,学生画出分类示意图,同桌合作画出与分类对应的有理数树.2.丹丹在做第1题时,发现了新的分类方法,她认为:带“+”的数分为一类,带“-”的数分为一类,数的前面没有符号的作为一类.你认为她的分类方法对吗?若不对,你发现什么新的分类方法吗?例:将下列各数分别填入相应的集合中;正整数集合负分数集合正有理数集合非正数集合典例精讲例:观察下列各组数,请找出它们的规律,并在横线上填上相应的数字.6810-1014-16典例精讲
非正数集合 负数集合
整数集合 正分数集合 1、把下列各数填入表示它所在的数集的圈里:
-18, ,3.141 5,0,2 011, , -0.124 847 ,95%.
,3.141 5,95%,- 18, ,
- 0.124 847,
…- 18,0, ,
- 0.124 847,………- 18,0,2 011, 课堂作业2.下列说法:
①零是整数; ②零是有理数;
③零是自然数; ④零是正数;
⑤零是负数; ⑥零是非负数.
其中正确的有 ( )
A.4个 B.3个 C.2个 D.1个
A① 、②、③ 、⑥正确课堂作业3.下列说法错误的是 ( )
A.负整数和负分数统称为负有理数
B.正整数、0和负整数统称为整数
C.正有理数和负有理数组成全体有理数
D.3.14是小数,也是分数
C正有理数、0和负有理数组成全体有理数课堂作业4.下列叙述正确的是 ( )
A.存在最小的有理数
B.存在最小的正整数
C.存在最小的整数
D.存在最小的分数
B1课堂作业5.把下列各数填入相应集合的括号内:
27,―5.8,2 002, ,―1,90%,3.14,0, ,
―2,1,―0.01,π.
(1)整数集合:{ … } ;
(2)分数集合:{ …};
(3)负有理数集合:{ …} ;
(4)正有理数集合:{ …};
(5)非负整数集合:{ …}. 27,2 002,―1,0,―2,1, ―5.8,―1, ,―2,―0.01, 27,2 002,0,1, 27,2 002, ,90%,3.14,1,课堂作业6、最小的正整数是______,最大的负整数是_____,所有大于-4的负整数有_________,不大于3的非负整数有____________。1-1-1,-2,-30,1,2,37、下列说法正确的是( )
①1是最小的正有理数; ②-1是最大的负有理数;
③0是最小的非负有理数;④0是最大的非正有理数.
A.①② B.②③
C.③④ D.①④ C 课堂作业
2、有理数的分类:
(1)按整数与分数划分;
(2)按性质划分;3、如何区分整数和分数?4、如何理解非正数和非负数?5、整数和分数,正数和负数之间有什么关系?6、学会观察一列数字之间的规律;进步往往从归纳反思开始!课堂小结7、分类的基本原则:
(1)按同一标准分类
(2)不重不漏1、什么是有理数?有理数分类的注意事项:1,如 能约分成整数的数_____(填“能”或“不能”)算做分数;2,两个整数的比(如 等)、有限小数(如0.2,-
3.14等)、无限循环小数(如 等)都是分数;但
无限不循环小数(如 等)不是分数;不能3,无限不循环小数不是有理数;(无理数)4,整数中除了正整数和负整数,还有_____.0有理数还有其他的分类方法吗?课堂小结课后思考1、如果用字母表示一个数,那么
可能是什么样的数,一定为正数吗?
可能是正数,可能是负数,也可能是零.
2、观察下面一列数,探究其规律:
, , , , , ,…
(1)写出第7,8,9个数.
(2)如果这一列数无限排列下去,与哪两数越来越近?
课后思考课后思考4.说出下列生活情景中用到的数所属的集合.
⑴摩托车的里程表上读出的数;
⑵中央电视台播放的天气预报中,播报各地的气温所用到的数;
⑶老师批改试卷时用到的数;
⑷烤鸭店的柜台上的电子秤上读出的数;
⑸表示某一地区的海拔高度所用的数.3.依据生活情境回答问题:
①当夜空中繁星密布时,小贝贝在数星星,他所用到的数属于什么数?
②一把测量用的刻度尺上可以读出哪几类有理数?
③一支测量气温用的温度计,可以从上面读出哪几类有理数? 课后思考 猜谜:财政赤字(猜一数学名词)
答案:负数
2,0既不是正数,也不是负数.
3,正数与负数通常用来表示具有相反意义的
量.
4,“0”所表示的意思.
5,在生产中,通常用正负数来表示允许误差.举例讲解 女力士唐功红在女子+75公斤级举重比赛中,不负众望,以抓举122.5公斤,挺举182.5公斤,总成绩305公斤夺得第18枚金牌,与获银牌的韩国选手相比,她的抓举重量-7.5公斤,挺举重量+10公斤. 在女子柔道-52公斤级的冠军争夺战中,中国选手冼东妹仅用1.1分钟,就为中国柔道队夺得首枚金牌. 在男子110米栏决赛中,中国选手刘翔以12.91秒的成绩夺得金牌,这个成绩打破了12.96的奥运会纪录,平了世界纪录,实现了中国男子田径金牌0的突破.12.96, 182.5, 110,12.91,1.1,-520,+75,122.5,+10.-7.5,18,305,1.在以上各数中,哪些是在小学里学过的数?它们可以分为哪几类?2.在小学里学过的数中,有没有哪类数在上面没有出现?请举例说明.3.用计算器计算下列各分数的值,说明所有分数都可以化作什么数?4.由前面的结论,小学里学的数可以分为哪几类?零: 负分数:-52, -67, -1,-2,…0正整数:负整数:正整数集合正分数: +10,18,29,+75,12.96, -7.5,110,305,1,2,3,…182.5, 12.91,1.1,负整数集合举例讲解由刚才的演示可知:
1.有理数可分为哪两类数?探究有理数的分类(1)2.整数可分为哪几类?3.分数可分为哪几类?12345探索新知⑧ ① ② ③ ④ ⑤ ⑥ ⑦ 依据有理数的分类示意图,在右图的卡片上填上下列数的名称.你发现有理数的分类示意图与这棵树枝干的形状有哪些联系吗?正整数零负整数正分数负分数整数分数有理数例1:把下列各数填在相应的集合中:正数集合:{ };
负数集合:{ };
分数集合:{ };
整数集合:{ };
非负数集合:{ };
有理数集合:{ };注意:1、像 这种可以先化简成整数的数是
整数不是分数;2、非负整数集合包括正整数和0,也称为自然数集合.1.在右边的有理数中,正整数有:__________;负分数有:_____________________________;整数有:_______________________________;分数有:_______________________________.探究有理数的分类(2) 小组讨论,合作完成讨论题,集中交流,形成正确分类方法,学生画出分类示意图,同桌合作画出与分类对应的有理数树.2.丹丹在做第1题时,发现了新的分类方法,她认为:带“+”的数分为一类,带“-”的数分为一类,数的前面没有符号的作为一类.你认为她的分类方法对吗?若不对,你发现什么新的分类方法吗?例:将下列各数分别填入相应的集合中;正整数集合负分数集合正有理数集合非正数集合典例精讲例:观察下列各组数,请找出它们的规律,并在横线上填上相应的数字.6810-1014-16典例精讲
非正数集合 负数集合
整数集合 正分数集合 1、把下列各数填入表示它所在的数集的圈里:
-18, ,3.141 5,0,2 011, , -0.124 847 ,95%.
,3.141 5,95%,- 18, ,
- 0.124 847,
…- 18,0, ,
- 0.124 847,………- 18,0,2 011, 课堂作业2.下列说法:
①零是整数; ②零是有理数;
③零是自然数; ④零是正数;
⑤零是负数; ⑥零是非负数.
其中正确的有 ( )
A.4个 B.3个 C.2个 D.1个
A① 、②、③ 、⑥正确课堂作业3.下列说法错误的是 ( )
A.负整数和负分数统称为负有理数
B.正整数、0和负整数统称为整数
C.正有理数和负有理数组成全体有理数
D.3.14是小数,也是分数
C正有理数、0和负有理数组成全体有理数课堂作业4.下列叙述正确的是 ( )
A.存在最小的有理数
B.存在最小的正整数
C.存在最小的整数
D.存在最小的分数
B1课堂作业5.把下列各数填入相应集合的括号内:
27,―5.8,2 002, ,―1,90%,3.14,0, ,
―2,1,―0.01,π.
(1)整数集合:{ … } ;
(2)分数集合:{ …};
(3)负有理数集合:{ …} ;
(4)正有理数集合:{ …};
(5)非负整数集合:{ …}. 27,2 002,―1,0,―2,1, ―5.8,―1, ,―2,―0.01, 27,2 002,0,1, 27,2 002, ,90%,3.14,1,课堂作业6、最小的正整数是______,最大的负整数是_____,所有大于-4的负整数有_________,不大于3的非负整数有____________。1-1-1,-2,-30,1,2,37、下列说法正确的是( )
①1是最小的正有理数; ②-1是最大的负有理数;
③0是最小的非负有理数;④0是最大的非正有理数.
A.①② B.②③
C.③④ D.①④ C 课堂作业
2、有理数的分类:
(1)按整数与分数划分;
(2)按性质划分;3、如何区分整数和分数?4、如何理解非正数和非负数?5、整数和分数,正数和负数之间有什么关系?6、学会观察一列数字之间的规律;进步往往从归纳反思开始!课堂小结7、分类的基本原则:
(1)按同一标准分类
(2)不重不漏1、什么是有理数?有理数分类的注意事项:1,如 能约分成整数的数_____(填“能”或“不能”)算做分数;2,两个整数的比(如 等)、有限小数(如0.2,-
3.14等)、无限循环小数(如 等)都是分数;但
无限不循环小数(如 等)不是分数;不能3,无限不循环小数不是有理数;(无理数)4,整数中除了正整数和负整数,还有_____.0有理数还有其他的分类方法吗?课堂小结课后思考1、如果用字母表示一个数,那么
可能是什么样的数,一定为正数吗?
可能是正数,可能是负数,也可能是零.
2、观察下面一列数,探究其规律:
, , , , , ,…
(1)写出第7,8,9个数.
(2)如果这一列数无限排列下去,与哪两数越来越近?
课后思考课后思考4.说出下列生活情景中用到的数所属的集合.
⑴摩托车的里程表上读出的数;
⑵中央电视台播放的天气预报中,播报各地的气温所用到的数;
⑶老师批改试卷时用到的数;
⑷烤鸭店的柜台上的电子秤上读出的数;
⑸表示某一地区的海拔高度所用的数.3.依据生活情境回答问题:
①当夜空中繁星密布时,小贝贝在数星星,他所用到的数属于什么数?
②一把测量用的刻度尺上可以读出哪几类有理数?
③一支测量气温用的温度计,可以从上面读出哪几类有理数? 课后思考 猜谜:财政赤字(猜一数学名词)
答案:负数
