24.7向量的线性运算 学案
图片预览




文档简介
24.7平面向量的线性运算
【学习目标】
1.理解实数与向量相乘的意义.
2.知道实数与向量相乘的运算律.
3.在从数的运算到向量的运算的认识过程中体会类比的思想.
4.对于给定的一个非零实数和一个非零向量,能画出它们相乘所得的向量.
5.知道平行向量,会用向量关系式表示两个向量的平行关系.
6.在实数与向量相乘和平行向量定理的学习与应用中体会代数与几何的联系.
【主要概念】
1、向量的加法法则:一般的,几个向量相加,可把这几个向量顺次首尾相接,那么它们的和向量是以第一个向量为起点,最后一个向量的终点为终点的向量。这就是向量加法的多边形法则.
2、实数与向量相乘的运算:设为正整数,为向量,我们用表示个相加;用表示个相加.又当为正整数时,表示与同向且长度为的向量.
3、与的关系:k>0时,与的方向相同,且大小是︱︱的
k倍,K<0时,与的方向相反,且大小是︱︱的︱
k︱倍,K=0时=.
//
4、实数与向量相乘的运算律:
设m,n为实数,、是向量,则
(1);
(2);
(3).
【典型例题】
【例1】已知非零向量,求作
并指出他们的长度和方向.
解:在平面内任取一点O,作=。在射线OA上,取OB=
OA,则=
在射线OA的反向延长线上,取OC=.则=-。
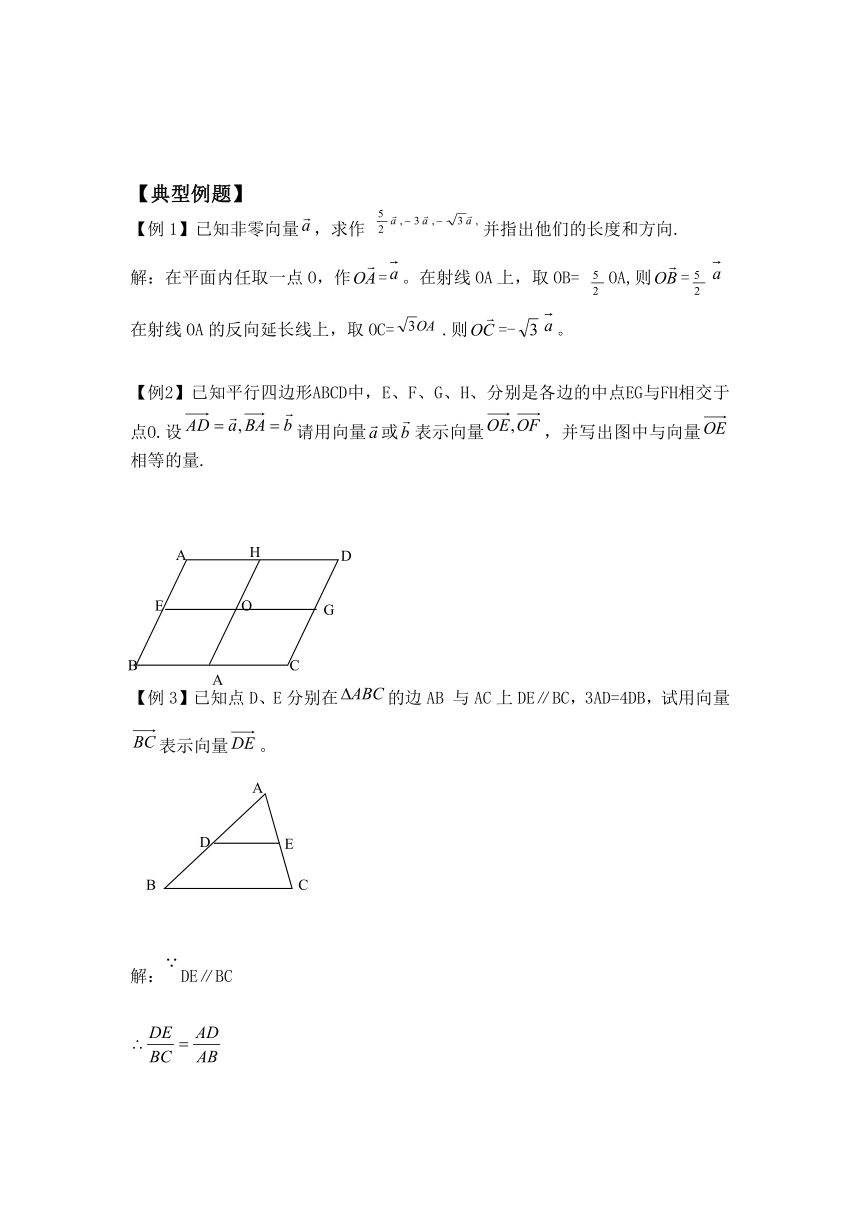
【例2】已知平行四边形ABCD中,E、F、G、H、分别是各边的中点EG与FH相交于点O.设请用向量或表示向量,并写出图中与向量相等的量.
【例3】已知点D、E分别在的边AB
与AC上DE∥BC,3AD=4DB,试用向量表示向量。
解:DE∥BC
由3AD=4DB
得
可知
得
方向相同,从而得出:
【例4】表示实数与向量相乘的运算,下列表示运算是否正确:
(1)表示为×或者·
(
正确
)
(2)表示(
错误
)
(3)表示
(
错误
)
【例5】计算
(1);
(2);
(3).
解:(1)原式=;
(2)原式==
(3)原式=
【例6】在矩形中,,,则向量的长等于(
)
(A)2
(B)
(C)3
(D)4
答案:
D
解析:
【例7】下面给出四个命题:
对于实数和向量、恒有:
对于实数、和向量,恒有
若,则有
若,则
其中正确命题的个数是(
)
(A)1
(B)2
(C)3
(D)4
答案:C
解析:根据实数与向量的积的定义及运算定律容易得出①、②、④正确,③不一定成立.
时,
但此时也不一定有成立
【例8】若a与b的方向相反,且,则a+b的方向与a的方向
;
此时
.
答案:相同;=;
解析:考察向量的加法运算以及模之间的关系。
【例9】已知D、E、F分别是△ABC的边BC、CA、AB的中点,且,,,则下列各式:①;②;③;④
.其中正确的等式的个数为
答案:2
解析:考察向量的加法运算。
【例10】已知A、B、C三点不共线,O是△ABC内的一点,若,则O是△ABC
的
。(填重心
、垂心、内心、外心之一)
答案:重心
解析:考察向量的运算与三角形的性质。
【例11】若则的取值范围是
答案:。
解析:由结论||a|-|b||≤|a±b|≤|a|+|b|,因为=。
【例12】如图,D、E、F是的边AB、BC、CA的中点,
则=
答案:
解析:向量可以自由平移的观点是本题的解题关键,平移的目的是便于按向量减法法则进行运算,由图可知∴
B组
【例13】在中,,M为BC的中点,则_______。(用表示)
答案:
解析:如图,,,
所以。
【例14】化简:=
.
答案:0
【例15】如图,ABCD是一个梯形,AB∥CD,且AB=2CD,M、N分别是DC和AB的中点,已知=a,=b,试用a,b表示和.
【解法一】
连结CN,则ANDC
∴四边形ANCD是平行四边形.
=-b,又∵+=0
∴=b-a
∴=-b+a=a-b
【解法二】
∵=0
即:a+(-a)+(-b)=0,∴=b-a
又∵在四边形ADMN中,有=0,
即:b+a++(-a)=0,∴a-b.
【例16】已知:在任意四边形ABCD中,E、F分别是AD、DC的中点.
求证:
解析:思路1:运用向量的图形语言、向量的多边形法则,进行向量的加法、减法运算以及向量的中点坐标公式.
证法一:(如图1),∵E、F分别是AD、DC的中点,
∴,
∵,
∴.
①
同理
.
②
由
①+②
得
.
∴.
证法二:连结EB、EC,(如图2),则
,,
∴
证法三:任取一点O,连结OA、OB、OC、OD、OE、OF(如图3),
∵E、F分别是AD、DC的中点,
∴,.
【随堂练习1】
1、设k是一个实数,是向量,那么k与相乘所得的积是一个
,记作
;
2、若与是互为相反向量,则若+=
;
3、已知非零向量若=,与的方向相同,它的长度是||的5倍,则=
;
4、如图,AD是中BC边上的中线,点G是的
重心,,
则=
,
=
;
5、已知:如图,在□ABCD中,对角线AC与BD相交于点O,
则与向量相等的向量是
;
与向量相反的向量是
;
与向量平行的向量是
;
若,则=
,
=
;
若,,则=
,
=
,=
;
6、已知:如图,在△ABC中,DE∥FG∥BC,AD∶DF∶FB=1∶1∶2,
,则
,=
,
=
,
,
=
;
7、下列式子中,错误的是………………………………………………(
).
(A);(B);(C);(D).
8、如果非零向量与满足等式,那么向量与的方向
.
9、已知向量,求作-3和.
10、如图,在□ABCD中,E、F、G、H分别为各边的中点,设,,试用向量、表示向量、和
11、在□ABCD中,AC与BD相交于点O,,在图中画出向量、、
12、如图,已知点D、E分别在△ABC的边AB、AC上,DE∥BC,且5AD=2DB,试用向量表示向量?
13、已知点D、E分别在△ABC的边AB、AC上,DE∥BC,且,试用向量表示向量?
【随堂练习2】
1.
2.
3.
4.当向量与单位向量方向相反,长度为2时,
5.若(),则(填“平行于”或“不平行于”)
6.⊿中,分别是边上的中点,若,则
7.若非零向量,则向量与方向是____,它们的位置关系是______.
8.若非零向量,则向量与方向是____,它们的长度关系是______.
9.若向量的长度是向量的长度的2倍,且,则.
10.已知矩形的对角线与交于点,如果,.
11.计算:(1).=
(2).=
12.已知:向量关系式:,试用,表示向量=
13.
设是一个平面内两个不平行的非零向量,,
则向量在向量方向上的分向量分别是____________.
【课后练习1】
1.化简:_____________.
2.下列关于向量的等式中,正确的是(
)
A.;
B.
;
C.;
D..
3.
对非零向量与,下列命题中假命题是
A.
若,则
B.
若,则
C.
若,则
D.
若
,则
4.在△ABC中,点D是边AB的中点,设,那么用、表示为________________.
5.如图,已知向量、、,那么下列结论正确的是
(A);
(B);
(C);
(D).
6.如图,在△ABC中,点D是边BC的中点,设
,
,用、的线性组合表示是
.
7.若向量与单位向量的方向相同,且,则=________.(用表示)
8.已知向量,,且,则向量=
.
9.如上图,梯形ABCD中,AB//CD。AC交BD于点O,AB=2CD.已知、,如用、
表示,那么=___________.
10.如图,在⊿ABC中,如果,那么等于(
)
(A)BC;
(B);
(C)CB;
(D).
11.
如果点C是线段AB的中点,那么下列结论中正确的是(
).
(A)
(B)
(C)
(D)
12.在梯形ABCD中,AD//BC,EF是梯形的中位线,点E在AB上,若AD︰BC=1︰3,,则用表示是:=
.
13.在□ABCD中,AC与BD相交于点O,,那么等于(
)
(A)
(B)
(C)
(D)
14.在矩形ABCD中,=,=1,则向量(++)的长度为___________.
15.已知在平行四边形ABCD中,向量、,那么向量等于___________.
16.已知AD是△ABC的中线,点G是△ABC的重心,,那么用向量表示向量为
.
17.在四边形ABCD中,E是AB边的中点,设,,那么用、表示
为
.
18.如图,平行四边形ABCD中,对角线AC、BD交于点O,下列等式成立的是(
)
(A);
(B);
(C);
(D)
19.如图,梯形中,∥,,
AB
,
CD
,请用向量表示向量
.
作图题:
20.已知是一个平面内两个不平行的非零向量.
求作:(1).(2).
21.已知非零向量和,求作(1)、(2)(不要求写作法).
解答题:
1.在⊿中,分别是的中点,交于点,
设
(1)分别用向量、表示
(2)用向量的线性组合表示
2.平行四边形中,对角线交于点,设
(1)用的线性组合表示;
(2)用的线性组合表示
3.在梯形中,
设
(1)用的线性组合表示求;
(2)用的线性组合表示求
【课后练习2】
一、选择题
1.已知、是两个非零向量,是一个单位向量,下列等式中正确的是(
)
;
(B);
(C);
(D).
2.下列判断不正确的是……………………………………………………………(
)
(A);
(B)如果,那么;
(C);
(D)如果(),那么.
5、在四边形ABCD中,向量AB、BC、CD的和向量是……………………………(
)
A、AC
B、DA
C、BD
D、AD
8.化简的结果是(
)
(A)
;
(B)
;
(C)
;
(D)
.
5.下列语句错误的是(
)
(A)如果或,那么;
(B)如果、是非零实数,是非零向量,那么;
(C)如果是一个非零向量,,那么∥;
(D)如果向量和非零向量平行,那么存在唯一的实数,使.
二、填空题
1.计算:=___________
2.
计算:=__________.
3.若与单位向量方向相反且长度为3,则
.
4.计算:
.
5.如果向量、满足关系式,用向量表示向量,则=
.
6.如右上图,在平行四边形ABCD中,点E、F分别是AB、CD上的中点,记.用含、的式子表示向量
.
7.
计算:
.
8.已知在梯形中,∥,是梯形的中位线,若,,则
(用表示).
9.若与单位向量方向相反且长度为5,则用单位向量表示为:
.
10.如果向量、满足关系式,用向量表示向量,则=
.
11.如图,
DE∥BC,且2AD=AB,试用向量表示向量:
.
12.在平行四边形ABCD中,若
=,
=,则
=
(用和表示).
13.如图,已知点D、E分别在△ABC的边AB、AC上,DE∥BC,且3AD=2DB,试用向量表示向量:
.
14.
已知直线l上依次有五个点A、B、C、D、E(如图),
满足AB=BC=CD=DE,如果把向量作为单位向量,
那么向量=
.(结果用单位向量表示)
15.如图,在中,是边的中点,是延长线上的点,且,试根据下列要求表示向量,
(1)用、表示____________________;
(2)用、表示_____________________.
三、作图题
1.如图,已知向量、,求作向量.
2.已知两个不平行的向量、,求作:.
【课后练习4】
1、下列命题中,正确的是(
)
A.||
=
||
= B.||
=
|
|且
//
=
C.
=
//
D.|
|
=
0
=
0
2、已知一个单位向量,设、是非零向量,则下列等式中正确的是:(
)
(A)
(B)
(C)
(D)
3、
若
且
,则四边形ABCD的形状为(
)
A.
平行四边形
B.
菱形
C.
矩形
D.
等腰梯形
4、若向量
=4、
=6,则
的最小值是
,
的最大值是
。
5、如图,点M是△CAB的边AB的中点,设
,
试用、的线性组合表示向量。
6、如图,已知平行四边形ABCD的对角线AC与BD相交于点O,设,分别求出向量关于的分解式。
7、如图,已知向量,,求作向量:(+)-2(-)
8、如图,已知向量、、,作出分别在、方向上的分向量
9、已知-=-,+=3,那么与平行吗?
10、如图,D是△ABC的边AC上的一点,AD=DC,E、F、G分别AD、BD、BC的中点。设=,=,试用向量、的线性组合表示向量
【课后练习5】
填空题(每题分,共计分)
若是非零向量,则的方向是:当时,与_______方向
如果两个非零向量满足(是非零实数),那么和一定是___________;当时,它们是__________的向量;当时,它们是___________的向量
设是非零实数,是非零向量,用式子表示实数与向量相乘对于向量加法的分配律:_______________________________________
如果是两个不平行的向量,那么叫做的______________________
对于非零向量,它的长度为,如果把与它同向的单位向量记作,那么向量可以记作____________
设是单位向量,若与方向相同,且满足,请用表示:________________
如果则_____________________
在四边形中,设,,如果那么四边形一定是_________(填四边形的名称)
已知的重心是点,则_______________
设是平行四边形的对角线的交点,点为平面内与不重合的任意一点,设,试用表示:________________________________
二、选择题(每题分,共计分)
下列式子中,错误的是(
)
A.
B.
C.
D.
向量化简后的结果等于(
)
A.
B.
C.
D.
点在线段上,且,若,则的值等于(
)
A.
B.
C.
D.
给出下列个命题,其中真命题的个数是(
)个
(1)单位向量都相等
(2)单位向量都平行
(3)平行的单位向量必相等
A.
B.
C.
D.
已知一个单位向量,设是非零向量,则下列等式中正确的是(
)
B.
C.
D.
三、解答题
计算:(满分分)
17.已知向量关系式,试用向量表示(满分分)
18.已知非零向量,请用作图方法验证(不写作图方法,保留作图痕迹,请写出验证过程)(满分分)
19.在中,为的三等分点,为三等分点,,写出关于的线性组合.(满分分)
20、如图,已知平行四边形中,点分别是边的中点,与对角线分别交于点,设,(满分分)
试用分别表示向量
作出向量分别在方向上的分向量
21、在中,是边的在中点,是延长线上的点,且.
(满分分)
用表示向量
用表示向量
22、在四边形中,请判断四边形的形状,并证明你的结论(满分分)
A
B
C
D
E
H
G
A
O
F
G
H
E
D
C
F
O
A
B
E
C
D
A
B
C
D
G
·
(图八)
B
A
A
B
C
E
D
A
B
C
E
D
B
A
C
D
A
B
C
D
O
(第5题图)
A
B
C
D
O
A
B
C
D
AC
AB
AD
→
→
→
→
→
→
→
F
E
D
C
B
A
E
D
B
C
A
DB
AD
AB
A
B
C
D
E
l
A
B
C
D
E
A
G
C
E
F
B
D
A
B
C
E
G
F
H
B
A
C
E
F
G
H
A
B
D
E
C
【学习目标】
1.理解实数与向量相乘的意义.
2.知道实数与向量相乘的运算律.
3.在从数的运算到向量的运算的认识过程中体会类比的思想.
4.对于给定的一个非零实数和一个非零向量,能画出它们相乘所得的向量.
5.知道平行向量,会用向量关系式表示两个向量的平行关系.
6.在实数与向量相乘和平行向量定理的学习与应用中体会代数与几何的联系.
【主要概念】
1、向量的加法法则:一般的,几个向量相加,可把这几个向量顺次首尾相接,那么它们的和向量是以第一个向量为起点,最后一个向量的终点为终点的向量。这就是向量加法的多边形法则.
2、实数与向量相乘的运算:设为正整数,为向量,我们用表示个相加;用表示个相加.又当为正整数时,表示与同向且长度为的向量.
3、与的关系:k>0时,与的方向相同,且大小是︱︱的
k倍,K<0时,与的方向相反,且大小是︱︱的︱
k︱倍,K=0时=.
//
4、实数与向量相乘的运算律:
设m,n为实数,、是向量,则
(1);
(2);
(3).
【典型例题】
【例1】已知非零向量,求作
并指出他们的长度和方向.
解:在平面内任取一点O,作=。在射线OA上,取OB=
OA,则=
在射线OA的反向延长线上,取OC=.则=-。
【例2】已知平行四边形ABCD中,E、F、G、H、分别是各边的中点EG与FH相交于点O.设请用向量或表示向量,并写出图中与向量相等的量.
【例3】已知点D、E分别在的边AB
与AC上DE∥BC,3AD=4DB,试用向量表示向量。
解:DE∥BC
由3AD=4DB
得
可知
得
方向相同,从而得出:
【例4】表示实数与向量相乘的运算,下列表示运算是否正确:
(1)表示为×或者·
(
正确
)
(2)表示(
错误
)
(3)表示
(
错误
)
【例5】计算
(1);
(2);
(3).
解:(1)原式=;
(2)原式==
(3)原式=
【例6】在矩形中,,,则向量的长等于(
)
(A)2
(B)
(C)3
(D)4
答案:
D
解析:
【例7】下面给出四个命题:
对于实数和向量、恒有:
对于实数、和向量,恒有
若,则有
若,则
其中正确命题的个数是(
)
(A)1
(B)2
(C)3
(D)4
答案:C
解析:根据实数与向量的积的定义及运算定律容易得出①、②、④正确,③不一定成立.
时,
但此时也不一定有成立
【例8】若a与b的方向相反,且,则a+b的方向与a的方向
;
此时
.
答案:相同;=;
解析:考察向量的加法运算以及模之间的关系。
【例9】已知D、E、F分别是△ABC的边BC、CA、AB的中点,且,,,则下列各式:①;②;③;④
.其中正确的等式的个数为
答案:2
解析:考察向量的加法运算。
【例10】已知A、B、C三点不共线,O是△ABC内的一点,若,则O是△ABC
的
。(填重心
、垂心、内心、外心之一)
答案:重心
解析:考察向量的运算与三角形的性质。
【例11】若则的取值范围是
答案:。
解析:由结论||a|-|b||≤|a±b|≤|a|+|b|,因为=。
【例12】如图,D、E、F是的边AB、BC、CA的中点,
则=
答案:
解析:向量可以自由平移的观点是本题的解题关键,平移的目的是便于按向量减法法则进行运算,由图可知∴
B组
【例13】在中,,M为BC的中点,则_______。(用表示)
答案:
解析:如图,,,
所以。
【例14】化简:=
.
答案:0
【例15】如图,ABCD是一个梯形,AB∥CD,且AB=2CD,M、N分别是DC和AB的中点,已知=a,=b,试用a,b表示和.
【解法一】
连结CN,则ANDC
∴四边形ANCD是平行四边形.
=-b,又∵+=0
∴=b-a
∴=-b+a=a-b
【解法二】
∵=0
即:a+(-a)+(-b)=0,∴=b-a
又∵在四边形ADMN中,有=0,
即:b+a++(-a)=0,∴a-b.
【例16】已知:在任意四边形ABCD中,E、F分别是AD、DC的中点.
求证:
解析:思路1:运用向量的图形语言、向量的多边形法则,进行向量的加法、减法运算以及向量的中点坐标公式.
证法一:(如图1),∵E、F分别是AD、DC的中点,
∴,
∵,
∴.
①
同理
.
②
由
①+②
得
.
∴.
证法二:连结EB、EC,(如图2),则
,,
∴
证法三:任取一点O,连结OA、OB、OC、OD、OE、OF(如图3),
∵E、F分别是AD、DC的中点,
∴,.
【随堂练习1】
1、设k是一个实数,是向量,那么k与相乘所得的积是一个
,记作
;
2、若与是互为相反向量,则若+=
;
3、已知非零向量若=,与的方向相同,它的长度是||的5倍,则=
;
4、如图,AD是中BC边上的中线,点G是的
重心,,
则=
,
=
;
5、已知:如图,在□ABCD中,对角线AC与BD相交于点O,
则与向量相等的向量是
;
与向量相反的向量是
;
与向量平行的向量是
;
若,则=
,
=
;
若,,则=
,
=
,=
;
6、已知:如图,在△ABC中,DE∥FG∥BC,AD∶DF∶FB=1∶1∶2,
,则
,=
,
=
,
,
=
;
7、下列式子中,错误的是………………………………………………(
).
(A);(B);(C);(D).
8、如果非零向量与满足等式,那么向量与的方向
.
9、已知向量,求作-3和.
10、如图,在□ABCD中,E、F、G、H分别为各边的中点,设,,试用向量、表示向量、和
11、在□ABCD中,AC与BD相交于点O,,在图中画出向量、、
12、如图,已知点D、E分别在△ABC的边AB、AC上,DE∥BC,且5AD=2DB,试用向量表示向量?
13、已知点D、E分别在△ABC的边AB、AC上,DE∥BC,且,试用向量表示向量?
【随堂练习2】
1.
2.
3.
4.当向量与单位向量方向相反,长度为2时,
5.若(),则(填“平行于”或“不平行于”)
6.⊿中,分别是边上的中点,若,则
7.若非零向量,则向量与方向是____,它们的位置关系是______.
8.若非零向量,则向量与方向是____,它们的长度关系是______.
9.若向量的长度是向量的长度的2倍,且,则.
10.已知矩形的对角线与交于点,如果,.
11.计算:(1).=
(2).=
12.已知:向量关系式:,试用,表示向量=
13.
设是一个平面内两个不平行的非零向量,,
则向量在向量方向上的分向量分别是____________.
【课后练习1】
1.化简:_____________.
2.下列关于向量的等式中,正确的是(
)
A.;
B.
;
C.;
D..
3.
对非零向量与,下列命题中假命题是
A.
若,则
B.
若,则
C.
若,则
D.
若
,则
4.在△ABC中,点D是边AB的中点,设,那么用、表示为________________.
5.如图,已知向量、、,那么下列结论正确的是
(A);
(B);
(C);
(D).
6.如图,在△ABC中,点D是边BC的中点,设
,
,用、的线性组合表示是
.
7.若向量与单位向量的方向相同,且,则=________.(用表示)
8.已知向量,,且,则向量=
.
9.如上图,梯形ABCD中,AB//CD。AC交BD于点O,AB=2CD.已知、,如用、
表示,那么=___________.
10.如图,在⊿ABC中,如果,那么等于(
)
(A)BC;
(B);
(C)CB;
(D).
11.
如果点C是线段AB的中点,那么下列结论中正确的是(
).
(A)
(B)
(C)
(D)
12.在梯形ABCD中,AD//BC,EF是梯形的中位线,点E在AB上,若AD︰BC=1︰3,,则用表示是:=
.
13.在□ABCD中,AC与BD相交于点O,,那么等于(
)
(A)
(B)
(C)
(D)
14.在矩形ABCD中,=,=1,则向量(++)的长度为___________.
15.已知在平行四边形ABCD中,向量、,那么向量等于___________.
16.已知AD是△ABC的中线,点G是△ABC的重心,,那么用向量表示向量为
.
17.在四边形ABCD中,E是AB边的中点,设,,那么用、表示
为
.
18.如图,平行四边形ABCD中,对角线AC、BD交于点O,下列等式成立的是(
)
(A);
(B);
(C);
(D)
19.如图,梯形中,∥,,
AB
,
CD
,请用向量表示向量
.
作图题:
20.已知是一个平面内两个不平行的非零向量.
求作:(1).(2).
21.已知非零向量和,求作(1)、(2)(不要求写作法).
解答题:
1.在⊿中,分别是的中点,交于点,
设
(1)分别用向量、表示
(2)用向量的线性组合表示
2.平行四边形中,对角线交于点,设
(1)用的线性组合表示;
(2)用的线性组合表示
3.在梯形中,
设
(1)用的线性组合表示求;
(2)用的线性组合表示求
【课后练习2】
一、选择题
1.已知、是两个非零向量,是一个单位向量,下列等式中正确的是(
)
;
(B);
(C);
(D).
2.下列判断不正确的是……………………………………………………………(
)
(A);
(B)如果,那么;
(C);
(D)如果(),那么.
5、在四边形ABCD中,向量AB、BC、CD的和向量是……………………………(
)
A、AC
B、DA
C、BD
D、AD
8.化简的结果是(
)
(A)
;
(B)
;
(C)
;
(D)
.
5.下列语句错误的是(
)
(A)如果或,那么;
(B)如果、是非零实数,是非零向量,那么;
(C)如果是一个非零向量,,那么∥;
(D)如果向量和非零向量平行,那么存在唯一的实数,使.
二、填空题
1.计算:=___________
2.
计算:=__________.
3.若与单位向量方向相反且长度为3,则
.
4.计算:
.
5.如果向量、满足关系式,用向量表示向量,则=
.
6.如右上图,在平行四边形ABCD中,点E、F分别是AB、CD上的中点,记.用含、的式子表示向量
.
7.
计算:
.
8.已知在梯形中,∥,是梯形的中位线,若,,则
(用表示).
9.若与单位向量方向相反且长度为5,则用单位向量表示为:
.
10.如果向量、满足关系式,用向量表示向量,则=
.
11.如图,
DE∥BC,且2AD=AB,试用向量表示向量:
.
12.在平行四边形ABCD中,若
=,
=,则
=
(用和表示).
13.如图,已知点D、E分别在△ABC的边AB、AC上,DE∥BC,且3AD=2DB,试用向量表示向量:
.
14.
已知直线l上依次有五个点A、B、C、D、E(如图),
满足AB=BC=CD=DE,如果把向量作为单位向量,
那么向量=
.(结果用单位向量表示)
15.如图,在中,是边的中点,是延长线上的点,且,试根据下列要求表示向量,
(1)用、表示____________________;
(2)用、表示_____________________.
三、作图题
1.如图,已知向量、,求作向量.
2.已知两个不平行的向量、,求作:.
【课后练习4】
1、下列命题中,正确的是(
)
A.||
=
||
= B.||
=
|
|且
//
=
C.
=
//
D.|
|
=
0
=
0
2、已知一个单位向量,设、是非零向量,则下列等式中正确的是:(
)
(A)
(B)
(C)
(D)
3、
若
且
,则四边形ABCD的形状为(
)
A.
平行四边形
B.
菱形
C.
矩形
D.
等腰梯形
4、若向量
=4、
=6,则
的最小值是
,
的最大值是
。
5、如图,点M是△CAB的边AB的中点,设
,
试用、的线性组合表示向量。
6、如图,已知平行四边形ABCD的对角线AC与BD相交于点O,设,分别求出向量关于的分解式。
7、如图,已知向量,,求作向量:(+)-2(-)
8、如图,已知向量、、,作出分别在、方向上的分向量
9、已知-=-,+=3,那么与平行吗?
10、如图,D是△ABC的边AC上的一点,AD=DC,E、F、G分别AD、BD、BC的中点。设=,=,试用向量、的线性组合表示向量
【课后练习5】
填空题(每题分,共计分)
若是非零向量,则的方向是:当时,与_______方向
如果两个非零向量满足(是非零实数),那么和一定是___________;当时,它们是__________的向量;当时,它们是___________的向量
设是非零实数,是非零向量,用式子表示实数与向量相乘对于向量加法的分配律:_______________________________________
如果是两个不平行的向量,那么叫做的______________________
对于非零向量,它的长度为,如果把与它同向的单位向量记作,那么向量可以记作____________
设是单位向量,若与方向相同,且满足,请用表示:________________
如果则_____________________
在四边形中,设,,如果那么四边形一定是_________(填四边形的名称)
已知的重心是点,则_______________
设是平行四边形的对角线的交点,点为平面内与不重合的任意一点,设,试用表示:________________________________
二、选择题(每题分,共计分)
下列式子中,错误的是(
)
A.
B.
C.
D.
向量化简后的结果等于(
)
A.
B.
C.
D.
点在线段上,且,若,则的值等于(
)
A.
B.
C.
D.
给出下列个命题,其中真命题的个数是(
)个
(1)单位向量都相等
(2)单位向量都平行
(3)平行的单位向量必相等
A.
B.
C.
D.
已知一个单位向量,设是非零向量,则下列等式中正确的是(
)
B.
C.
D.
三、解答题
计算:(满分分)
17.已知向量关系式,试用向量表示(满分分)
18.已知非零向量,请用作图方法验证(不写作图方法,保留作图痕迹,请写出验证过程)(满分分)
19.在中,为的三等分点,为三等分点,,写出关于的线性组合.(满分分)
20、如图,已知平行四边形中,点分别是边的中点,与对角线分别交于点,设,(满分分)
试用分别表示向量
作出向量分别在方向上的分向量
21、在中,是边的在中点,是延长线上的点,且.
(满分分)
用表示向量
用表示向量
22、在四边形中,请判断四边形的形状,并证明你的结论(满分分)
A
B
C
D
E
H
G
A
O
F
G
H
E
D
C
F
O
A
B
E
C
D
A
B
C
D
G
·
(图八)
B
A
A
B
C
E
D
A
B
C
E
D
B
A
C
D
A
B
C
D
O
(第5题图)
A
B
C
D
O
A
B
C
D
AC
AB
AD
→
→
→
→
→
→
→
F
E
D
C
B
A
E
D
B
C
A
DB
AD
AB
A
B
C
D
E
l
A
B
C
D
E
A
G
C
E
F
B
D
A
B
C
E
G
F
H
B
A
C
E
F
G
H
A
B
D
E
C
