11.2与三角形有关的角同步练习(解析版)
文档属性
| 名称 | 11.2与三角形有关的角同步练习(解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 366.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-18 08:25:03 | ||
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
新人教版八年级数学上册同步练习
11.2与三角形有关的角
一、单选题
1、如图,AD是△ABC的高,已知∠B=44°, 则∠BAD 的度数是( )
A、44° B、46° C、54° D、56°
2、如图所示,∠1+∠2+∠3+∠4的度数为( )
A、100° B、180° C、360° D、无法确定
3、如果一个角的两边分别垂直于另一个角的两边,那么这两个角的数量关系为( )
A、相等 B、互补 C、相等或互补 D、无法确定
4、如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C的度数为( )
A、50° B、40° C、30° D、20°
5、如图,已知AB∥CD,则∠α的度数是( )
A、60° B、25° C、75° D、85°
6、下列能判定三角形是等腰三角形的是( )
A、有两个角为30°、60° B、有两个角为40°、80°
C、有两个角为50°、80° D、有两个角为100°、120°
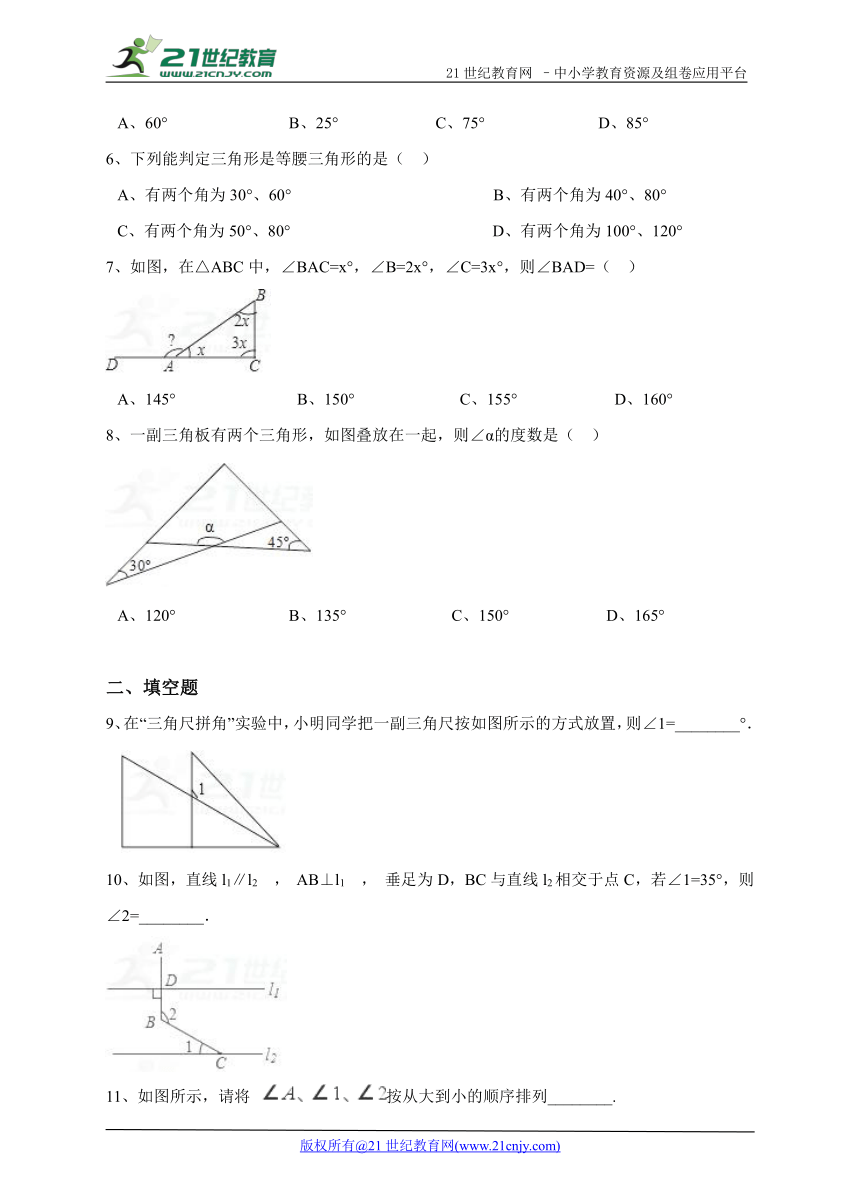
7、如图,在△ABC中,∠BAC=x°,∠B=2x°,∠C=3x°,则∠BAD=( )
A、145° B、150° C、155° D、160°
8、一副三角板有两个三角形,如图叠放在一起,则∠α的度数是( )
A、120° B、135° C、150° D、165°
二、填空题
9、在“三角尺拼角”实验中,小明同学把一副三角尺按如图所示的方式放置,则∠1=________°.
10、如图,直线l1∥l2 , AB⊥l1 , 垂足为D,BC与直线l2相交于点C,若∠1=35°,则∠2=________.
21世纪教育网版权所有
11、如图所示,请将 按从大到小的顺序排列________.
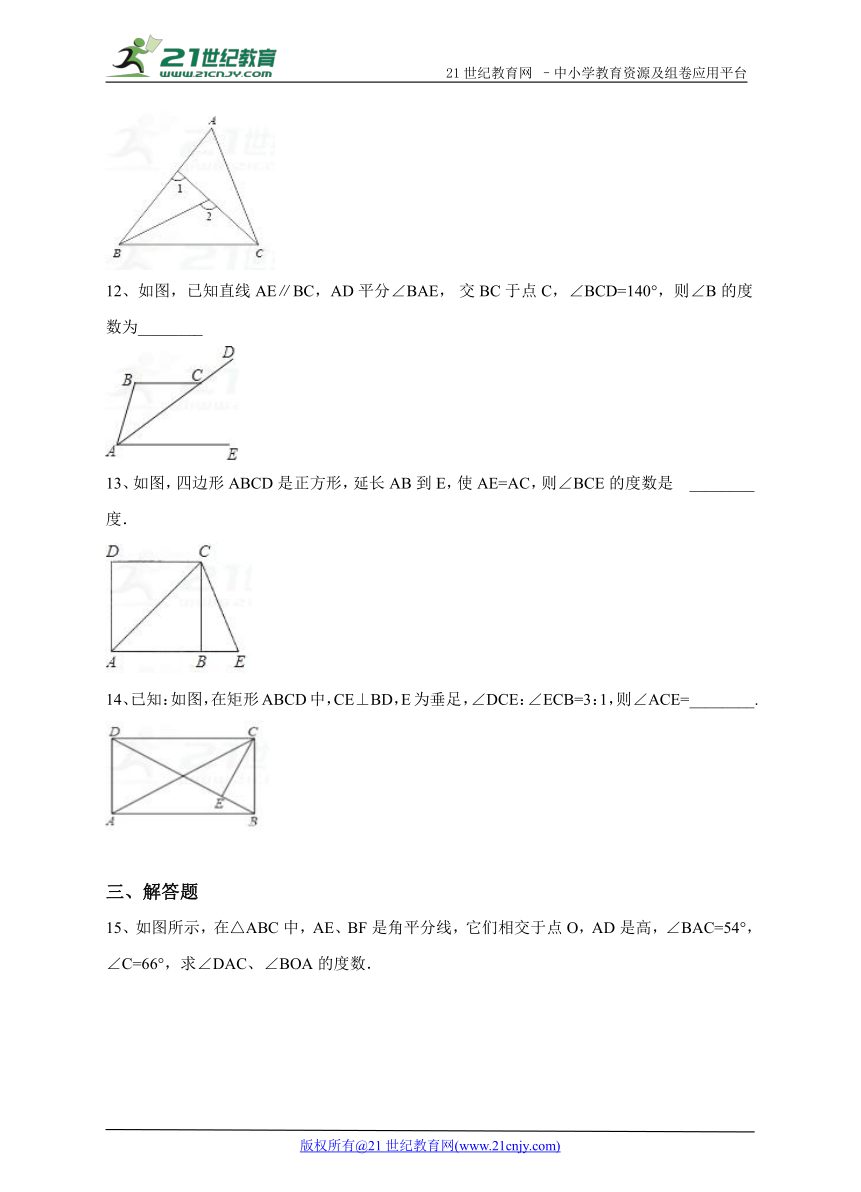
12、如图,已知直线AE∥BC,AD平分∠BAE, 交BC于点C,∠BCD=140°,则∠B的度数为________
21教育网
13、如图,四边形ABCD是正方形,延长AB到E,使AE=AC,则∠BCE的度数是 ________度.
21cnjy.com
14、已知:如图,在矩形ABCD中,CE⊥BD,E为垂足,∠DCE:∠ECB=3:1,则∠ACE=________.
21·cn·jy·com
三、解答题
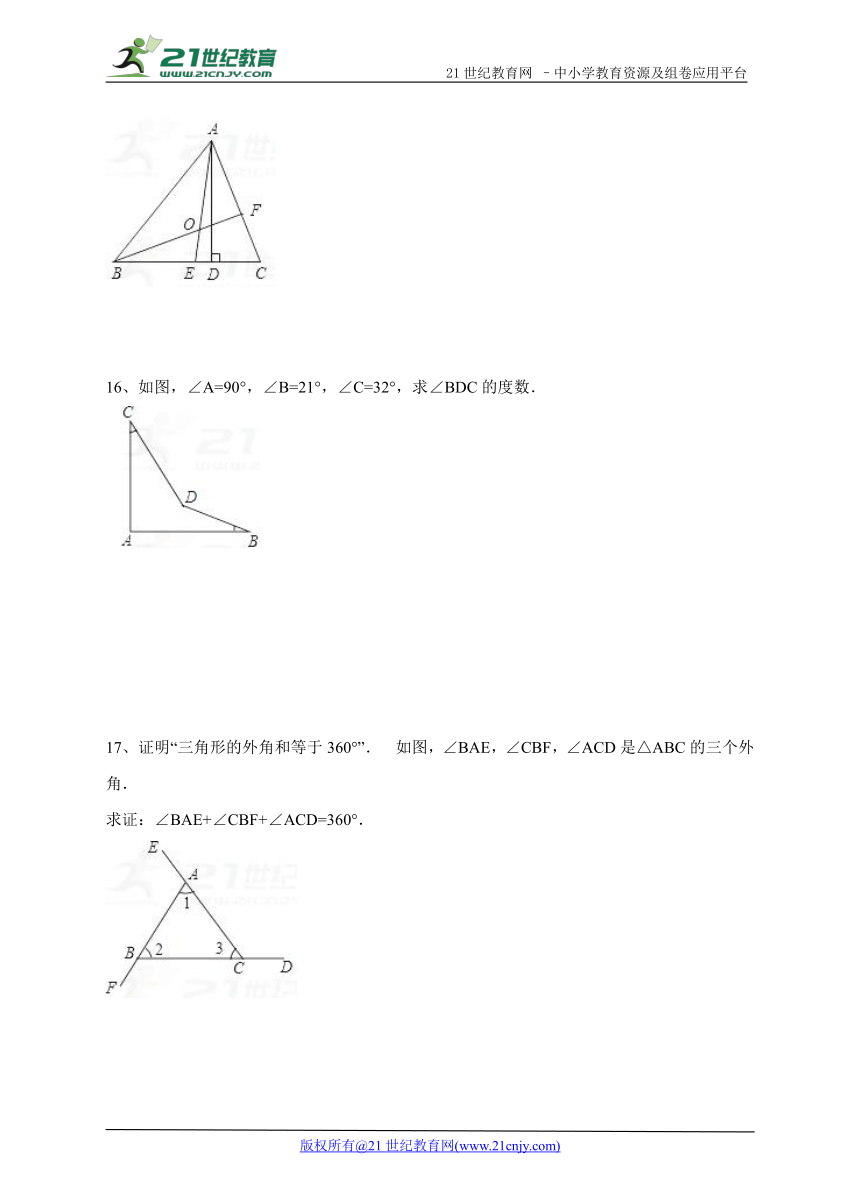
15、如图所示,在△ABC中,AE、BF是角平分线,它们相交于点O,AD是高,∠BAC=54°,∠C=66°,求∠DAC、∠BOA的度数.
www.21-cn-jy.com
16、如图,∠A=90°,∠B=21°,∠C=32°,求∠BDC的度数.
17、证明“三角形的外角和等于360°”. 如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角.
求证:∠BAE+∠CBF+∠ACD=360°.
2·1·c·n·j·y
18、有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C.△ABC中,∠A=50°,求∠DBA+∠DCA的度数.【来源:21·世纪·教育·网】
参考答案与试题解析
一、单选题
1、B
解:∵AD是△ABC的高
∴∠B+∠BAD=90
∴∠BAD=90°-44°=46°,
故选B. 21·世纪*教育网
2、C
解:把题中的图形分成两个三角形,再根据三角形的内角和定理求解即可.
由图可得∠1+∠2+∠3+∠4=360°,故选C.
3、C
解:如图:
图1中,根据垂直的量相等的角都等于90°,对顶角相等,所以∠1=∠2,
图2中,同样根据垂直的量相等的角都等于90°,根据四边形的内角和等于360°,所以∠1+∠2=360° 90° 90°=180°
所以如果一个角的两边与另一个角的两边分别垂直,那么这两个角的关系是相等或互补,
故选C. www-2-1-cnjy-com
4、C
解:∵AD∥BC , ∠B=30°,
∴∠EAD=∠B=30°.
又∵AD是∠EAC的平分线,
∴∠EAC=2∠EAD=60°.
∵∠EAC=∠B+∠C ,
∴∠C=∠EAC-∠B=30°.
故选C.
5、C
解:如图,延长AB、CF交于点E, ∵AB∥CD,
∴∠C=∠E=15°,
∵∠ABF=120°,
∴∠EBF=60°,
∵∠α是△BEF的外角,
∴∠α=∠E+∠EBF=15°+60°=75°.
故选:C.
2-1-c-n-j-y
6、C
解:A,因为有两个角为30°、60°,则第三个角为90°,所以此选项不正确; B,因为有两个角为40°、80°,则第三个角为60°,所以此选项不正确;
C,因为有两个角为50°、80°,则第三个角为50°,有两个角相等,所以此选项正确;
D,因为100°+120°>180°,所以此选项不正确;
故选C. 21*cnjy*com
7、B
解:在△ABC中,∵∠B+∠C+∠BAC=180°,∠BAC=x°,∠B=2x°,∠C=3x°, ∴6x=180,
∴x=30,
∵∠BAD=∠B+∠C=5x=150°,
故选B.
【来源:21cnj*y.co*m】
8、D
解:如图,由三角形的外角性质得,∠1=45°+90°=135°, ∠α=∠1+30°=135°+30°=165°.
故选D.
【出处:21教育名师】
二、填空题
9、120
解:由三角形的外角的性质可知,∠1=90°+30°=120°, 故答案为:120.
10、125°
解:延长AB交直线l2于M,
∵直线l1∥l2 , AB⊥l1 ,
∴AM⊥直线l2 ,
∴∠BME=90°,
∴∠2=∠1+∠BME=90°+35°=125°
故答案为:125°. 【版权所有:21教育】
11、
根解:由三角形的外角的性质得,∠2>∠1,∠1>∠A,
∴∠2>∠1>∠A,
故答案为:∠2>∠1>∠A. 21*cnjy*com
12、100°
解:∵∠BCD=140°,∴∠ACB=180°-140°=40°.
∵AE∥BC , ∴∠CAE=∠ACB=40°.
∵AD平分∠BAE , ∴∠BAC=∠CAE=40°.
∴∠B=180°-40°-40°=100°.
13、22.5
解:∵四边形ABCD是正方形, ∴∠CAB=∠BCA=45°;
△ACE中,AC=AE,则:
∠ACE=∠AEC=(180°﹣∠CAE)=67.5°;
∴∠BCE=∠ACE﹣∠ACB=22.5°.
故答案为22.5.
14、45°
解:.∵四边形ABCD是矩形,
∴∠DCB=90°,
∵∠DCE:∠ECB=3:1,
∴∠DCE=×90°=67.5°,∠ECB=22.5°
∴∠EBC=∠ACB=90°-∠ECB=67.5°
∴∠ACE=∠ACB-∠ECB=67.5°-22.5°=45°.
三、解答题
15、解:∵AD是高,∴∠ADC=90° ,
∵∠C=66°,
∴∠DAC=180°﹣90°﹣66°=24°
∵∠BAC=54°,∠C=66°,AE是角平分线,
∴∠BAO=27°,∠ABC=60°
∵BF是∠ABC的角平分线 ,
∴∠ABO=30°,
∴∠BOA=180°﹣∠BAO﹣∠ABO=123°.
16、解:如图,连接AD并延长AD至点E,
∵∠BDE=∠BAE+∠B,∠CDE=∠CAD+∠C
∴∠BDC=∠BDE+∠CDE=∠CAD+∠C+∠BAD+∠B=∠BAC+∠B+∠C
∵∠A=90°,∠B=21°,∠C=32°,
∴∠BDC=90°+21°+32°=143°.
17、证法1:∵平角等于180°, ∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=180°×3=540°,
∴∠BAE+∠CBF+∠ACD=540°﹣(∠1+∠2+∠3).
∵∠1+∠2+∠3=180°,
∴∠BAE+∠CBF+∠ACD=540°﹣180°=360°.
证法2:∵∠BAE=∠2+∠3,∠CBF=∠1+∠3,∠ACD=∠1+∠2,
∴∠BAE+∠CBF+∠ACD=2(∠1+∠2+∠3),
∵∠1+∠2+∠3=180°,
∴∠BAE+∠CBF+∠ACD=360°.
18、解:∵∠A=50°, ∴∠ABC+∠ACB=180°﹣50°=130°,
而∠D=90°,
∴∠DBC+∠DCB=90°,
∴∠DBA+∠DCA=(∠ABC+∠ACB)﹣(∠DBC+∠DCB)
=130°﹣90°
=40°. 21教育名师原创作品
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
新人教版八年级数学上册同步练习
11.2与三角形有关的角
一、单选题
1、如图,AD是△ABC的高,已知∠B=44°, 则∠BAD 的度数是( )
A、44° B、46° C、54° D、56°
2、如图所示,∠1+∠2+∠3+∠4的度数为( )
A、100° B、180° C、360° D、无法确定
3、如果一个角的两边分别垂直于另一个角的两边,那么这两个角的数量关系为( )
A、相等 B、互补 C、相等或互补 D、无法确定
4、如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C的度数为( )
A、50° B、40° C、30° D、20°
5、如图,已知AB∥CD,则∠α的度数是( )
A、60° B、25° C、75° D、85°
6、下列能判定三角形是等腰三角形的是( )
A、有两个角为30°、60° B、有两个角为40°、80°
C、有两个角为50°、80° D、有两个角为100°、120°
7、如图,在△ABC中,∠BAC=x°,∠B=2x°,∠C=3x°,则∠BAD=( )
A、145° B、150° C、155° D、160°
8、一副三角板有两个三角形,如图叠放在一起,则∠α的度数是( )
A、120° B、135° C、150° D、165°
二、填空题
9、在“三角尺拼角”实验中,小明同学把一副三角尺按如图所示的方式放置,则∠1=________°.
10、如图,直线l1∥l2 , AB⊥l1 , 垂足为D,BC与直线l2相交于点C,若∠1=35°,则∠2=________.
21世纪教育网版权所有
11、如图所示,请将 按从大到小的顺序排列________.
12、如图,已知直线AE∥BC,AD平分∠BAE, 交BC于点C,∠BCD=140°,则∠B的度数为________
21教育网
13、如图,四边形ABCD是正方形,延长AB到E,使AE=AC,则∠BCE的度数是 ________度.
21cnjy.com
14、已知:如图,在矩形ABCD中,CE⊥BD,E为垂足,∠DCE:∠ECB=3:1,则∠ACE=________.
21·cn·jy·com
三、解答题
15、如图所示,在△ABC中,AE、BF是角平分线,它们相交于点O,AD是高,∠BAC=54°,∠C=66°,求∠DAC、∠BOA的度数.
www.21-cn-jy.com
16、如图,∠A=90°,∠B=21°,∠C=32°,求∠BDC的度数.
17、证明“三角形的外角和等于360°”. 如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角.
求证:∠BAE+∠CBF+∠ACD=360°.
2·1·c·n·j·y
18、有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C.△ABC中,∠A=50°,求∠DBA+∠DCA的度数.【来源:21·世纪·教育·网】
参考答案与试题解析
一、单选题
1、B
解:∵AD是△ABC的高
∴∠B+∠BAD=90
∴∠BAD=90°-44°=46°,
故选B. 21·世纪*教育网
2、C
解:把题中的图形分成两个三角形,再根据三角形的内角和定理求解即可.
由图可得∠1+∠2+∠3+∠4=360°,故选C.
3、C
解:如图:
图1中,根据垂直的量相等的角都等于90°,对顶角相等,所以∠1=∠2,
图2中,同样根据垂直的量相等的角都等于90°,根据四边形的内角和等于360°,所以∠1+∠2=360° 90° 90°=180°
所以如果一个角的两边与另一个角的两边分别垂直,那么这两个角的关系是相等或互补,
故选C. www-2-1-cnjy-com
4、C
解:∵AD∥BC , ∠B=30°,
∴∠EAD=∠B=30°.
又∵AD是∠EAC的平分线,
∴∠EAC=2∠EAD=60°.
∵∠EAC=∠B+∠C ,
∴∠C=∠EAC-∠B=30°.
故选C.
5、C
解:如图,延长AB、CF交于点E, ∵AB∥CD,
∴∠C=∠E=15°,
∵∠ABF=120°,
∴∠EBF=60°,
∵∠α是△BEF的外角,
∴∠α=∠E+∠EBF=15°+60°=75°.
故选:C.
2-1-c-n-j-y
6、C
解:A,因为有两个角为30°、60°,则第三个角为90°,所以此选项不正确; B,因为有两个角为40°、80°,则第三个角为60°,所以此选项不正确;
C,因为有两个角为50°、80°,则第三个角为50°,有两个角相等,所以此选项正确;
D,因为100°+120°>180°,所以此选项不正确;
故选C. 21*cnjy*com
7、B
解:在△ABC中,∵∠B+∠C+∠BAC=180°,∠BAC=x°,∠B=2x°,∠C=3x°, ∴6x=180,
∴x=30,
∵∠BAD=∠B+∠C=5x=150°,
故选B.
【来源:21cnj*y.co*m】
8、D
解:如图,由三角形的外角性质得,∠1=45°+90°=135°, ∠α=∠1+30°=135°+30°=165°.
故选D.
【出处:21教育名师】
二、填空题
9、120
解:由三角形的外角的性质可知,∠1=90°+30°=120°, 故答案为:120.
10、125°
解:延长AB交直线l2于M,
∵直线l1∥l2 , AB⊥l1 ,
∴AM⊥直线l2 ,
∴∠BME=90°,
∴∠2=∠1+∠BME=90°+35°=125°
故答案为:125°. 【版权所有:21教育】
11、
根解:由三角形的外角的性质得,∠2>∠1,∠1>∠A,
∴∠2>∠1>∠A,
故答案为:∠2>∠1>∠A. 21*cnjy*com
12、100°
解:∵∠BCD=140°,∴∠ACB=180°-140°=40°.
∵AE∥BC , ∴∠CAE=∠ACB=40°.
∵AD平分∠BAE , ∴∠BAC=∠CAE=40°.
∴∠B=180°-40°-40°=100°.
13、22.5
解:∵四边形ABCD是正方形, ∴∠CAB=∠BCA=45°;
△ACE中,AC=AE,则:
∠ACE=∠AEC=(180°﹣∠CAE)=67.5°;
∴∠BCE=∠ACE﹣∠ACB=22.5°.
故答案为22.5.
14、45°
解:.∵四边形ABCD是矩形,
∴∠DCB=90°,
∵∠DCE:∠ECB=3:1,
∴∠DCE=×90°=67.5°,∠ECB=22.5°
∴∠EBC=∠ACB=90°-∠ECB=67.5°
∴∠ACE=∠ACB-∠ECB=67.5°-22.5°=45°.
三、解答题
15、解:∵AD是高,∴∠ADC=90° ,
∵∠C=66°,
∴∠DAC=180°﹣90°﹣66°=24°
∵∠BAC=54°,∠C=66°,AE是角平分线,
∴∠BAO=27°,∠ABC=60°
∵BF是∠ABC的角平分线 ,
∴∠ABO=30°,
∴∠BOA=180°﹣∠BAO﹣∠ABO=123°.
16、解:如图,连接AD并延长AD至点E,
∵∠BDE=∠BAE+∠B,∠CDE=∠CAD+∠C
∴∠BDC=∠BDE+∠CDE=∠CAD+∠C+∠BAD+∠B=∠BAC+∠B+∠C
∵∠A=90°,∠B=21°,∠C=32°,
∴∠BDC=90°+21°+32°=143°.
17、证法1:∵平角等于180°, ∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=180°×3=540°,
∴∠BAE+∠CBF+∠ACD=540°﹣(∠1+∠2+∠3).
∵∠1+∠2+∠3=180°,
∴∠BAE+∠CBF+∠ACD=540°﹣180°=360°.
证法2:∵∠BAE=∠2+∠3,∠CBF=∠1+∠3,∠ACD=∠1+∠2,
∴∠BAE+∠CBF+∠ACD=2(∠1+∠2+∠3),
∵∠1+∠2+∠3=180°,
∴∠BAE+∠CBF+∠ACD=360°.
18、解:∵∠A=50°, ∴∠ABC+∠ACB=180°﹣50°=130°,
而∠D=90°,
∴∠DBC+∠DCB=90°,
∴∠DBA+∠DCA=(∠ABC+∠ACB)﹣(∠DBC+∠DCB)
=130°﹣90°
=40°. 21教育名师原创作品
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
