11.3多边形及其内角和同步练习(解析版)
文档属性
| 名称 | 11.3多边形及其内角和同步练习(解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 237.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-18 08:24:50 | ||
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
新人教版八年级数学上册同步练习
11.3多边形及其内角和
一、单选题
1、多边形的外角和等于( )
A、180° B、360° C、720° D、(n﹣2) 180°
2、一个多边形从一个顶点最多能引出三条对角线,这个多边形是( )
A、三角形 B、四边形 C、五边形 D、六边形
3、一个正多边形的边长为2,每个内角为135°,则这个多边形的周长是( )
A、8 B、12 C、16 D、18
4、若凸多边形的每个外角均为40°,过该多边形一个顶点的所有对角线条数是( )
A、6 B、8 C、18 D、27
5、若正多边形的一个内角是150°,则该正多边形的边数是( )
A、6 B、12 C、16 D、18
6、一个n边形共有20条对角线,则n的值为( )
A、5 B、6 C、8 D、10
7、十五边形从一个顶点出发有 ( )条对角线.
A、11 B、12 C、13 D、14
8、如果n边形每一个内角等于与它相邻外角的2倍,则n的值是( )
A、4 B、5 C、6 D、7
二、填空题
9、五边形从一个顶点出发,能引出________条对角线,一共有________条对角线.
10、一个多边形的内角和为1080°,则这个多边形的边数是________.
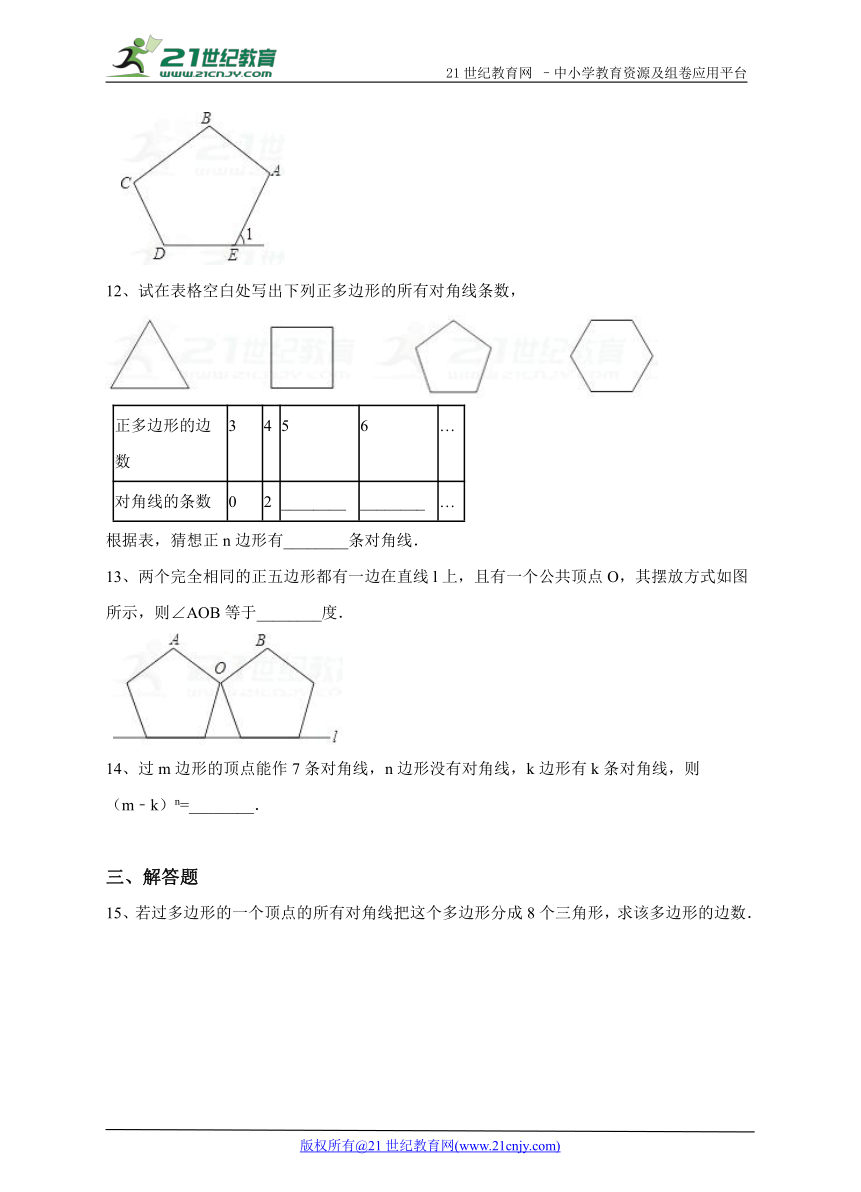
11、如图,∠1是五边形ABCDE的一个外角,若∠1=65°,则∠A+∠B+∠C+∠D=________°.
12、试在表格空白处写出下列正多边形的所有对角线条数,
正多边形的边数 3 4 5 6 …
对角线的条数 0 2 ________ ________ …
根据表,猜想正n边形有________条对角线.
13、两个完全相同的正五边形都有一边在直线l上,且有一个公共顶点O,其摆放方式如图所示,则∠AOB等于________度. 21cnjy.com
14、过m边形的顶点能作7条对角线,n边形没有对角线,k边形有k条对角线,则
(m﹣k)n=________.
三、解答题
15、若过多边形的一个顶点的所有对角线把这个多边形分成8个三角形,求该多边形的边数.
16、已知从n边形的一个顶点出发共有4条对角线,其周长为56,且各边长是连续的自然数,求这个多边形的各边长.21·cn·jy·com
17、如图,求:∠A+∠B+∠C+∠D+∠E+∠F的度数.
18、阅读下列内容,并答题:
我们知道计算n边形的对角线条数公式为, 如果有一个n边形的对角线一共有20条,则可以得到方程=20,去分母得n(n﹣3)=40;∵n为大于等于3的整数,且n比n﹣3的值大3,∴满足积为40且相差3的因数只有8和5,符合方程n(n﹣3)=40的整数n=8,即多边形是八边形.根据以上内容,问:
(1)若有一个多边形的对角线一共有14条,求这个多边形的边数;
(2)A同学说:“我求得一个多边形的对角线一共有30条.”你认为A同学说地正确吗?为什么? 【来源:21·世纪·教育·网】
参考答案与试题解析
一、单选题
1、B
解:多边形的外角和是360°,
故选:B.
2、D
解:设多边形有n条边, 则n﹣3=3,解得n=6.
故多边形的边数为6.
故选D.
3、C
解:∵正多边形的一个内角为135°,
∴外角是180﹣135=45°,
∵360÷45=8,
则这个多边形是八边形,
∴这个多边形的周长=2×8=16,
故选C. 21·世纪*教育网
4、A
解:这个多边形的边数是:360÷40=9, ∴过该多边形一个顶点的所有对角线条数是9﹣3=6条,
故选A. www-2-1-cnjy-com
5、B
解:设多边形为n边形,由题意,得 (n﹣2) 180°=150n,
解得n=12,
故选:B.
6、C
解:设这个多边形是n边形,则=20,
∴n2﹣3n﹣40=0,
(n﹣8)(n+5)=0,
解得n=8,n=﹣5(舍去).
故选C 21*cnjy*com
7、B
解:n边形(n>3)从一个顶点出发可以引(n﹣3)条对角线,所以十五边形从一个顶点出发有:15﹣3=12条对角线. 故选:B. 【来源:21cnj*y.co*m】
8、C
解:设外角为x,则相邻的内角为2x, 由题意得,2x+x=180°,
解得,x=60°,
360÷60°=6,
故选:C.
【出处:21教育名师】
二、填空题
9、2;5
解:五边形从一个顶点出发,能引出2条对角线,一共有5条对角线. 故答案为:2;5.
10、8
解:根据n边形的内角和公式,得 (n﹣2) 180=1080,
解得n=8.
∴这个多边形的边数是8.
故答案为:8. 【版权所有:21教育】
11、425
解:∵∠1=65°, ∴∠AED=115°,
∴∠A+∠B+∠C+∠D=540°﹣∠AED=425°,
故答案为:425.
12、5;9;
解:从四边形的一个顶点出发可画1条对角线,从五边形的一个顶点出发可画2条对角线,从六边形的一个顶点出发可画3条对角线,请猜想从七边形的一个顶点出发有4条对角线,从n边形的一个顶点出发有(n﹣3)条对角线,从而推导出n边形共有 条对角线, =5(条),
=9(条).
填表如下:21教育名师原创作品
正多边形的边数 3 4 5 6 …
对角线的条数 0 2 5 9 …
故答案为:5,9,.
13、108
解:如图
,
由正五边形的内角和,得∠1=∠2=∠3=∠4=108°,
∠5=∠6=180°﹣108°=72°,
∠7=180°﹣72°﹣72°=36°.
∠AOB=360°﹣108°﹣108°﹣36°=108°,
故答案为:108. 21世纪教育网版权所有
14、125
解:∵n边形从一个顶点发出的对角线有n﹣3条, ∴m=7+3=10,n=3,k=5,h=4;
∴(m﹣k)n=(10﹣5)3=125,
故答案为:125.
21教育网
三、解答题
15、解:设该多边形的边长为n,则
n﹣2=8,
解得:n=10.
答:该多边形是10边形.
www.21-cn-jy.com
16、解:依题意有n﹣3=4,
解得n=7,
设最短边为x,则
7x+1+2+3+4+5+6=56,
解得x=5.
故这个多边形的各边长是5,6,7,8,9,10,11.
2·1·c·n·j·y
17、解:如图,
∵∠BPO是△PDC的外角,
∴∠BPO=∠C+∠D,
∵∠POA是△OEF的外角,
∴∠POA=∠E+∠F,
∵∠A+∠B+∠BPO+∠POA=360°,
2-1-c-n-j-y
18、解:(1)方程=14,
去分母得:n(n﹣3)=28;
∵n为大于等于3的整数,且n比n﹣3的值大3,
∴满足积为28且相差3的因数只有7和4,
符合方程的整数n=7,即多边形是七边形.
(2)解:A同学说法是不正确的,
∵方程=30,去分母得n(n﹣3)=60;
符合方程n(n﹣3)=60的正整数n不存在,即多边形的对角线不可能有30条.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
新人教版八年级数学上册同步练习
11.3多边形及其内角和
一、单选题
1、多边形的外角和等于( )
A、180° B、360° C、720° D、(n﹣2) 180°
2、一个多边形从一个顶点最多能引出三条对角线,这个多边形是( )
A、三角形 B、四边形 C、五边形 D、六边形
3、一个正多边形的边长为2,每个内角为135°,则这个多边形的周长是( )
A、8 B、12 C、16 D、18
4、若凸多边形的每个外角均为40°,过该多边形一个顶点的所有对角线条数是( )
A、6 B、8 C、18 D、27
5、若正多边形的一个内角是150°,则该正多边形的边数是( )
A、6 B、12 C、16 D、18
6、一个n边形共有20条对角线,则n的值为( )
A、5 B、6 C、8 D、10
7、十五边形从一个顶点出发有 ( )条对角线.
A、11 B、12 C、13 D、14
8、如果n边形每一个内角等于与它相邻外角的2倍,则n的值是( )
A、4 B、5 C、6 D、7
二、填空题
9、五边形从一个顶点出发,能引出________条对角线,一共有________条对角线.
10、一个多边形的内角和为1080°,则这个多边形的边数是________.
11、如图,∠1是五边形ABCDE的一个外角,若∠1=65°,则∠A+∠B+∠C+∠D=________°.
12、试在表格空白处写出下列正多边形的所有对角线条数,
正多边形的边数 3 4 5 6 …
对角线的条数 0 2 ________ ________ …
根据表,猜想正n边形有________条对角线.
13、两个完全相同的正五边形都有一边在直线l上,且有一个公共顶点O,其摆放方式如图所示,则∠AOB等于________度. 21cnjy.com
14、过m边形的顶点能作7条对角线,n边形没有对角线,k边形有k条对角线,则
(m﹣k)n=________.
三、解答题
15、若过多边形的一个顶点的所有对角线把这个多边形分成8个三角形,求该多边形的边数.
16、已知从n边形的一个顶点出发共有4条对角线,其周长为56,且各边长是连续的自然数,求这个多边形的各边长.21·cn·jy·com
17、如图,求:∠A+∠B+∠C+∠D+∠E+∠F的度数.
18、阅读下列内容,并答题:
我们知道计算n边形的对角线条数公式为, 如果有一个n边形的对角线一共有20条,则可以得到方程=20,去分母得n(n﹣3)=40;∵n为大于等于3的整数,且n比n﹣3的值大3,∴满足积为40且相差3的因数只有8和5,符合方程n(n﹣3)=40的整数n=8,即多边形是八边形.根据以上内容,问:
(1)若有一个多边形的对角线一共有14条,求这个多边形的边数;
(2)A同学说:“我求得一个多边形的对角线一共有30条.”你认为A同学说地正确吗?为什么? 【来源:21·世纪·教育·网】
参考答案与试题解析
一、单选题
1、B
解:多边形的外角和是360°,
故选:B.
2、D
解:设多边形有n条边, 则n﹣3=3,解得n=6.
故多边形的边数为6.
故选D.
3、C
解:∵正多边形的一个内角为135°,
∴外角是180﹣135=45°,
∵360÷45=8,
则这个多边形是八边形,
∴这个多边形的周长=2×8=16,
故选C. 21·世纪*教育网
4、A
解:这个多边形的边数是:360÷40=9, ∴过该多边形一个顶点的所有对角线条数是9﹣3=6条,
故选A. www-2-1-cnjy-com
5、B
解:设多边形为n边形,由题意,得 (n﹣2) 180°=150n,
解得n=12,
故选:B.
6、C
解:设这个多边形是n边形,则=20,
∴n2﹣3n﹣40=0,
(n﹣8)(n+5)=0,
解得n=8,n=﹣5(舍去).
故选C 21*cnjy*com
7、B
解:n边形(n>3)从一个顶点出发可以引(n﹣3)条对角线,所以十五边形从一个顶点出发有:15﹣3=12条对角线. 故选:B. 【来源:21cnj*y.co*m】
8、C
解:设外角为x,则相邻的内角为2x, 由题意得,2x+x=180°,
解得,x=60°,
360÷60°=6,
故选:C.
【出处:21教育名师】
二、填空题
9、2;5
解:五边形从一个顶点出发,能引出2条对角线,一共有5条对角线. 故答案为:2;5.
10、8
解:根据n边形的内角和公式,得 (n﹣2) 180=1080,
解得n=8.
∴这个多边形的边数是8.
故答案为:8. 【版权所有:21教育】
11、425
解:∵∠1=65°, ∴∠AED=115°,
∴∠A+∠B+∠C+∠D=540°﹣∠AED=425°,
故答案为:425.
12、5;9;
解:从四边形的一个顶点出发可画1条对角线,从五边形的一个顶点出发可画2条对角线,从六边形的一个顶点出发可画3条对角线,请猜想从七边形的一个顶点出发有4条对角线,从n边形的一个顶点出发有(n﹣3)条对角线,从而推导出n边形共有 条对角线, =5(条),
=9(条).
填表如下:21教育名师原创作品
正多边形的边数 3 4 5 6 …
对角线的条数 0 2 5 9 …
故答案为:5,9,.
13、108
解:如图
,
由正五边形的内角和,得∠1=∠2=∠3=∠4=108°,
∠5=∠6=180°﹣108°=72°,
∠7=180°﹣72°﹣72°=36°.
∠AOB=360°﹣108°﹣108°﹣36°=108°,
故答案为:108. 21世纪教育网版权所有
14、125
解:∵n边形从一个顶点发出的对角线有n﹣3条, ∴m=7+3=10,n=3,k=5,h=4;
∴(m﹣k)n=(10﹣5)3=125,
故答案为:125.
21教育网
三、解答题
15、解:设该多边形的边长为n,则
n﹣2=8,
解得:n=10.
答:该多边形是10边形.
www.21-cn-jy.com
16、解:依题意有n﹣3=4,
解得n=7,
设最短边为x,则
7x+1+2+3+4+5+6=56,
解得x=5.
故这个多边形的各边长是5,6,7,8,9,10,11.
2·1·c·n·j·y
17、解:如图,
∵∠BPO是△PDC的外角,
∴∠BPO=∠C+∠D,
∵∠POA是△OEF的外角,
∴∠POA=∠E+∠F,
∵∠A+∠B+∠BPO+∠POA=360°,
2-1-c-n-j-y
18、解:(1)方程=14,
去分母得:n(n﹣3)=28;
∵n为大于等于3的整数,且n比n﹣3的值大3,
∴满足积为28且相差3的因数只有7和4,
符合方程的整数n=7,即多边形是七边形.
(2)解:A同学说法是不正确的,
∵方程=30,去分母得n(n﹣3)=60;
符合方程n(n﹣3)=60的正整数n不存在,即多边形的对角线不可能有30条.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
