第五章 平行四边形单元测试卷(解析版)
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
〖鲁教版五四制八年级上数学单元测试卷〗
第五章《平行四边形》
(时间:90分钟,总分100分)
题 号 一 二 三 总 分
得 分
班级: 姓名: 考号:
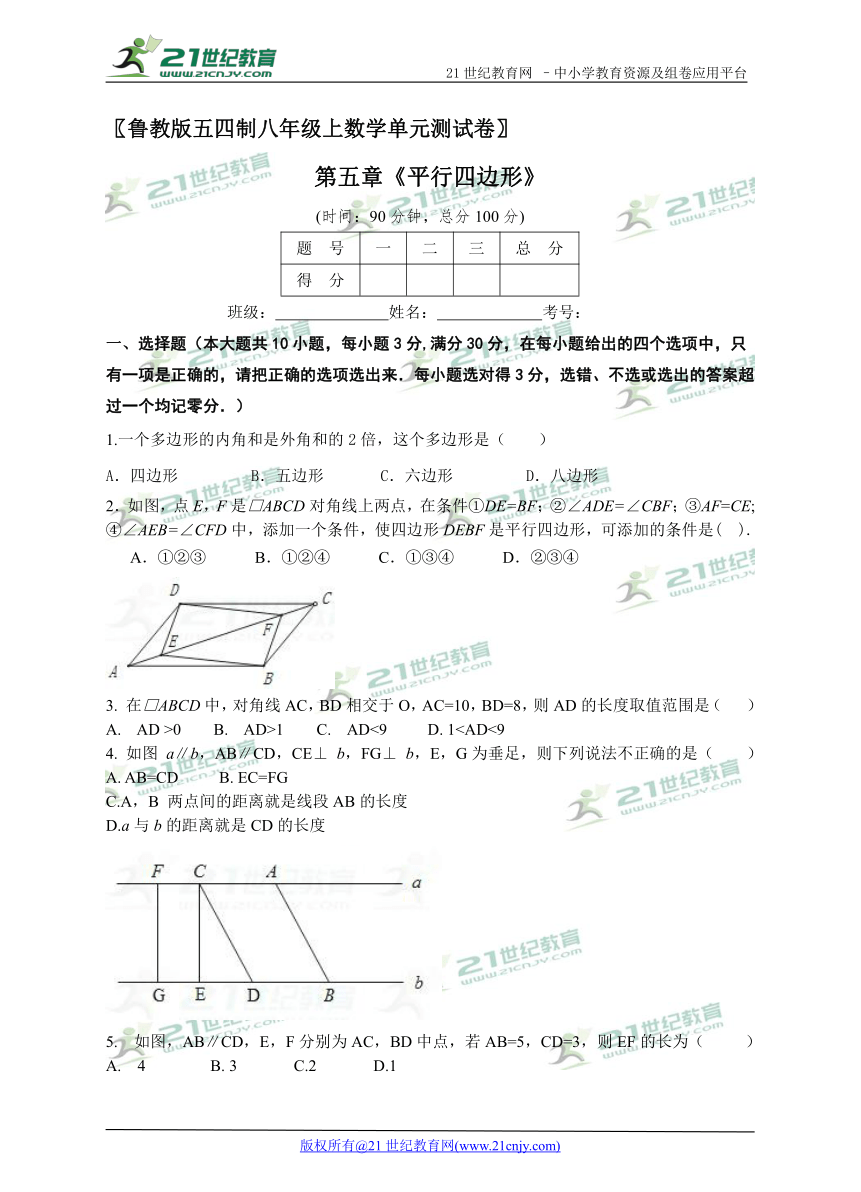
一、选择题(本大题共10小题,每小题3分,满分30分,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分.)21·世纪*教育网
1.一个多边形的内角和是外角和的2倍,这个多边形是( )
A.四边形 B.五边形 C.六边形 D.八边形
2.如图,点E,F是□ABCD对角线上两点,在条件①DE=BF;②∠ADE=∠CBF;③AF=CE; ④∠AEB=∠CFD中,添加一个条件,使四边形DEBF是平行四边形,可添加的条件是( ).
A.①②③ B.①②④ C.①③④ D.②③④
3. 在□ABCD中,对角线AC,BD相交于O,AC=10,BD=8,则AD的长度取值范围是( )
A. AD >0 B. AD>1 C. AD<9 D. 14. 如图 a∥b,AB∥CD,CE⊥ b,FG⊥ b,E,G为垂足,则下列说法不正确的是( )
A. AB=CD B. EC=FG
C.A,B 两点间的距离就是线段AB的长度
D.a与b的距离就是CD的长度
5. 如图,AB∥CD,E,F分别为AC,BD中点,若AB=5,CD=3,则EF的长为( )
A. 4 B. 3 C.2 D.1
6. 如图,在△ABC中,点D在边BC上,BD=AB,BM⊥AD于点M,N是AC的中点,连接MN.若DC=16 cm,则MN的长为( A )21世纪教育网版权所有21*cnjy*com
A. 8 cm B. 10 cm C. 12 cm D. 14 cm
7.如图,平行四边形ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为 ( )
A.3cm B.4cm C.5m D.8cm
8. 如图,△ABC的面积为16,点D是BC边上一点,且BD=BC,点G是AB上一点,点H在△ABC内部,且四边形BDHG是平行四边形.则图中阴影的面积是( )
A. 3 B. 4 C. 5 D. 6
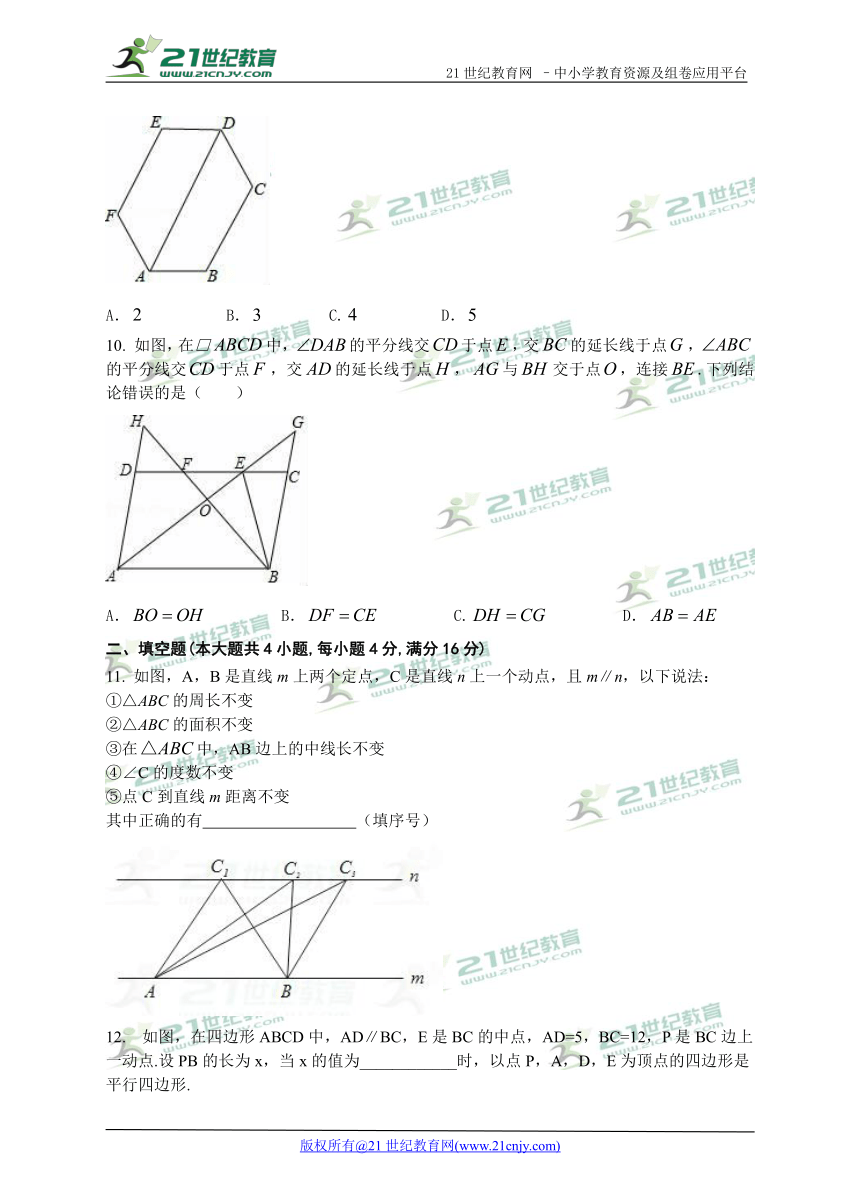
9.如图,六边形的内角都相等,,则下列结论成立的个数是
① ;②;③;④四边形是平行四边形;⑤六边形 即是中心对称图形,又是轴对称图形( )
A. B. C. D.
10. 如图,在□中,的平分线交于点,交的延长线于点,的平分线交于点,交的延长线于点,与交于点,连接.下列结论错误的是( )2-1-c-n-j-y【版权所有:21教育】
A. B. C. D.
二、填空题(本大题共4小题,每小题4分,满分16分)
11. 如图,A,B是直线m上两个定点,C是直线n上一个动点,且m∥n,以下说法:
①△ABC的周长不变
②△ABC的面积不变
③在中,AB边上的中线长不变
④∠C的度数不变
⑤点C到直线m距离不变
其中正确的有 (填序号)
12. 如图,在四边形ABCD中,AD∥BC,E是BC的中点,AD=5,BC=12,P是BC边上一动点.设PB的长为x,当x的值为____________时,以点P,A,D,E为顶点的四边形是平行四边形.2-1--j-y21*cnjy*com
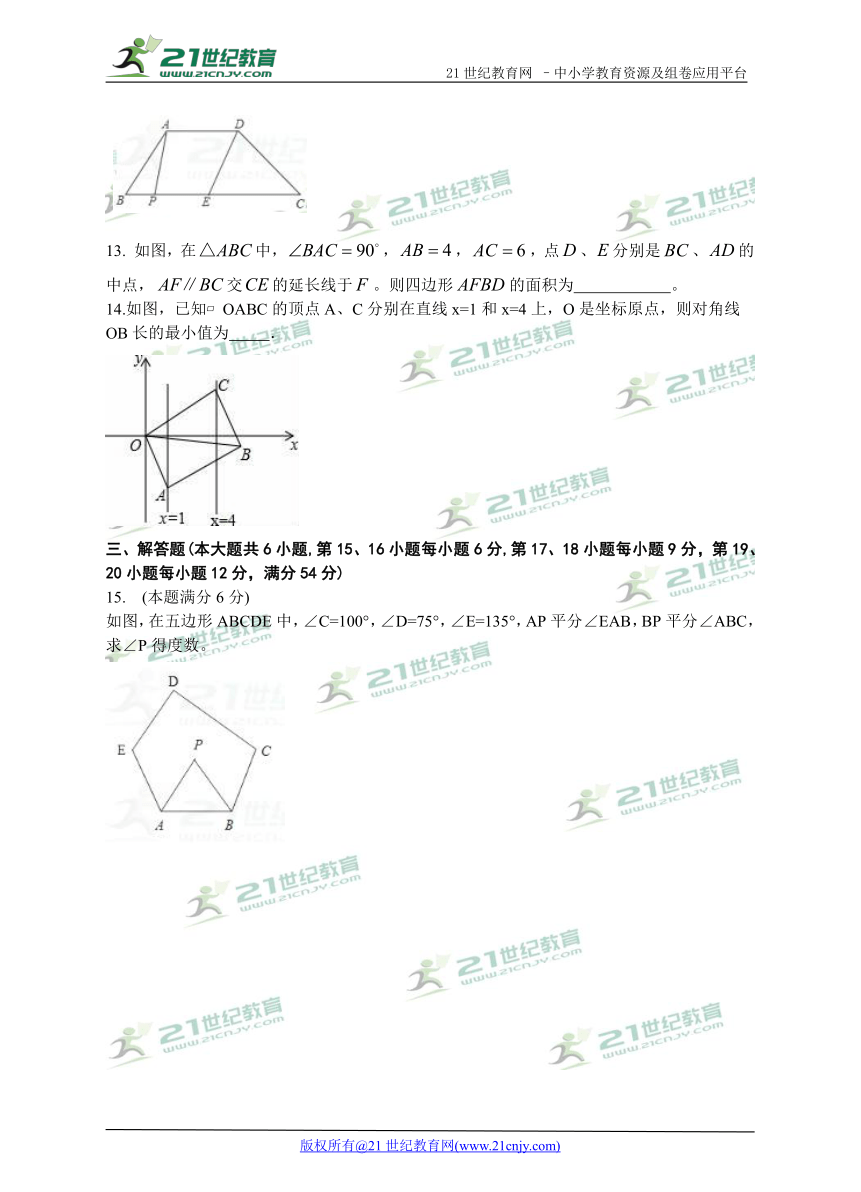
13. 如图,在中,,,,点、分别是、的中点,交的延长线于。则四边形的面积为 。
14.如图,已知 OABC的顶点A、C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为 .
三、解答题(本大题共6小题,第15、16小题每小题6分,第17、18小题每小题9分,第19、20小题每小题12分,满分54分)
15. (本题满分6分)
如图,在五边形ABCDE中,∠C=100°,∠D=75°,∠E=135°,AP平分∠EAB,BP平分∠ABC,求∠P得度数。
16. (本题满分6分)
已知,如图,平行四边形ABCD中,E是BC边的中点,连DE并延长交AB的延长线于点F,求证:AB=BF. www-2-1-cnjy-com21教育网
17. (本题满分9分)
提出命题:如图,在四边形ABCD中,∠A=∠C,∠ABC=∠ADC,求证:四边形ABCD是平行四边形.21教育名师原创作品
小明提供了如下解答过程:
证明:连接BD.
∵∠1+∠3=180 -∠A,∠2+∠4=180 ―∠C,∠A=∠C,
∴ ∠1+∠3=∠2+∠4.
∵∠ABC=∠ADC,
∴∠1=∠4,∠2=∠3.
∴AB∥CD,AD∥BC.
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).
反思交流:(1)请问小明的解法正确吗?如果有错,说明错在何处,并给出正确的证明过程.
(2)用语言叙述上述命题:___________________________________________________.
运用探究:(3)下列条件中,能确定四边形ABCD是平行四边形的是( )
A. ∠A∶∠B∶∠C∶∠D=1∶2∶3∶4 B. ∠A∶∠B∶∠C∶∠D=1∶3∶1∶3
C. ∠A∶∠B∶∠C∶∠D=2∶3∶3∶2 D. ∠A∶∠B∶∠C∶∠D=1∶1∶3∶3
18. (本题满分9分)
如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
19. (本题满分12分)
在△ABC中,AB=AC,点D在边所在的直线上,过点D作DF∥AC交AB于点F,DE∥AB交直线AC于点E.
(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF= .
20. (本题满分12分)
如图1,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE(不需证明)。
(温馨提示:在图1中,连结BD,取BD的中点H,连结HE、HF,根据三角形中位线定理,证明HE=HF,从而∠1=∠2,再利用平行线性质,可证得∠BME=∠CNE。)
(1)如图2,在四边形ADBC中,AB与CD相交于点O,AB=CD,E、F分别是BC、AD的中点,连结EF,分别交DC、AB于点M、N,判断△OMN的形状,请直接写出结论;
(2)如图3,在△ABC中,AC>AB,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,与BA的延长线交于点G,若∠EFC=60°,连结GD,判断△AGD的形状并证明。
〖鲁教版五四制八年级上数学单元测试卷〗
第五章《平行四边形》答案与解析
1.【答案】:C
【解析】:
解:根据多边形的外角和为360°,可知其内角和为720°,因此可根据多边形的内角和公式(n-2)·180°=720°,解得n=6,故是六边形.
故选:C
考点:多边形的内外角和
2.【答案】: D
【解析】:
解:选D,理由
∵□ABCD
∴AD∥BC
∴∠DAE=∠BCF
∵∠ADE=∠CBF,DE=BF
∴△ADE≌△BCF
∴∠AED=∠CFB
∴∠DEF=∠BFE
DE∥BF
∵∠ADE=∠CBF
∴∠BEF=∠DFE
∴DF∥BE
∴四边形DEBF是平行四边形
故选D
3.【答案】:D
【解析】:
解:如图
∵AC=10,BD=8
∴AO=5,DO=4
∴1故选D
4.【答案】:D
【解析】:解:线段CD与平行线a,b不垂直,a与b的距离不是CD的长度,选项D错误
故选D
6.【答案】:A
【解析】:
解:∵BD=AB,BM⊥AD
∴AM= MD
∵N是AC的中点
∴MN=DC=8
故选A
7.【答案】:B
【解析】:
解:因为四边形ABCD是平行四边形,所以AD=BC.因为□ABCD的周长是26cm,所以AD=BC且AB+BC=13①.因为△AOD的周长比△AOB的周长多3cm,所以AD-AB=3,即BC-AB=3②.①+②,得2BC=16,所以BC=8.因为AC⊥AB,所以∠BAC=90°,又因为E是BC中点,所以AE=BC=×8=4.,故选择B.21世纪教育网版权所有
【解后反思】(1)在直角三角形中出现斜边中点时,一般利用“直角三角形斜边上的中线等于斜边的一半”求斜边上的中线长.(2)平行四边形的性质:对边平行且相等,对角相等,邻角互补,对角线互相平分.www-2-1-cnjy-com
【关键词】平行四边形的性质;直角三角形.
8.【答案】:B
【解析】:
解:设△ABC底边BC上的高为h,△AGH底边GH上的高为h1,△CGH底边GH上的高为h2,则有h=h1+h2.【出处:21教育名师】
S△ABC=BC h=16,
S阴影=S△AGH+S△CGH=GH h1+ GH h2=GH (h1+h2)=GH h.
∵四边形BDHG是平行四边形,且BD=BC,
∴GH=BD=BC.
∴S阴影= ×(BC h)= S△ABC=4.故选择B
【解后反思】具有整体思想,发现两阴影面积的高的和与△ABC的高的关系是解题关键.
【关键词】三角形的面积,平行四边形的性质,整体思想
9.【答案】:D
【解析】:
考点:1.平行四边形的判定和性质;2.平行线的判定和性质;3.轴对称图形;4.中心对称图形.
10.【答案】:D
【解析】:
解:∵四边形ABCD是平行四边形,
∴AH∥BG,AD=BC,
∴∠H=∠HBG,
∵∠HBG=∠HBA,
∴∠H=∠HBA,
∴AH=AB,同理可证BG=AB,
考点:1、平行四边形的性质,2、等腰三角形的判定和性质
二、填空题
11.【答案】:②⑤
【解析】:
解:②△ABC的底边AB不变,高是两平行线m,n之间距离不变,所以面积不变,此选项正确;
⑤点C到直线m距离是两平行线m,n之间距离,所以点C到直线m距离不变
故答案是②⑤
12.【答案】:11或3
【解析】:
解:∵E是BC的中点,BC=12
∴BE=6
分类讨论
①当P点运到到P1时
∵四边形PADE是平行四边形
∴P1E=AD=5
∴PB=x=3
②当P点运到到P2时
∵四边形EADP是平行四边形
∴P2E=AD=5
∴PB=x=11
综上所述:x=11或3
13.【答案】:12
【解析】:
解:∵,,,
∴BC=
∵点是的中点
∴BD=BC=
∵点、分别是、的中点
∴AD∥BF
∵
∴四边形FBDA是平行四边形
过A点作AG⊥BC
∵S△ABC=AB· AC=AG· BC
∴4×6=AG×
∴AG=
∴四边形的面积为:×=12
14.【答案】:5
【解析】:
解:当B在x轴上时,对角线OB长的最小,如图所示:直线x=1与x轴交于点D,直线x=4与x轴交于点E,21cnjy.com
根据题意得:∠ADO=∠CEB=90°,OD=1,OE=4,
∵四边形ABCD是平行四边形,
∴OA∥BC,OA=BC,
∴∠AOD=∠CBE,
在△AOD和△CBE中,
,
∴△AOD≌△CBE(AAS),
∴OD=BE=1,
∴OB=OE+BE=5;
故答案为:5.
三、解答题
15.【答案】:65°
【解析】:解:在五边形ABCDE中
∠C+∠D+∠E+∠EAB+∠ABC=540°
∵∠C=100°,∠D=75°,∠E=135°
∴∠EAB+∠ABC=230°
∵AP平分∠EAB,BP平分∠ABC
∴∠PAB+∠PBC=115°
∴∠P=65°
16.【答案】:证明见解析.
【解析】:1-c-n-j-y
证明:∵E是BC的中点,
∴CE=BE,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠DCB=∠FBE,
在△CED和△BEF中,
,
∴△CED≌△BEF(ASA),
∴CD=BF,
∴AB=BF.
考点:1.平行四边形的性质;2.全等三角形的判定与性质.
17.【答案】:
【解析】:
解:(1)小明的解法不正确,错在推出∠1+∠3=∠2+∠4后,由∠ABC=∠ADC,不能直接推出∠1=∠4,∠2=∠3.21·cn·jy·com
正确证明:因为∠A+∠ABC+∠C+∠ADC=360°,∠A=∠C,∠ABC=∠ADC,所以2∠A+
2∠ABC=360°.所以∠A+∠ABC=180°.所以AD∥BC.同理∠A+∠ADC=180°.所以AB∥CD.所以四边形ABCD是平行四边形.www.21-cn-jy.com
(2)两组对角分别相等的四边形是平行四边形
(3)B
18.【答案】:(1)见解析;(2)6
【解析】:
解:(1)证明:∵点D、E、F、G分别为线段AB、OB、OC、AC的中点,
∴DG为△ABC的中位线,EF为△OBC的中位线,
∴DG∥BC且DG=BC,EF∥BC且EF=BC,
∴DG∥EF,DG=EF,∴四边形DEFG是平行四边形.
(2)解:∵∠OBC和∠OCB互余,∴△OBC是直角三角形,∠BOC=90°.
∵M为EF的中点,∴OM为Rt△OEF斜边的中线,
∴EF=2OM=2×3=6,∴DG=EF=6.
【解后反思】(1)当两个三角形有一条公共边时,则它们所对的三角形的中位线相等且平行.当两个直角三角形有公共的斜边时,则它们斜边上的中线相等.2·1·c·n·j·y
(2)平行四边形的判定方法,可分别从边、角、对角线等不同角度去理解与记忆,应用时可根据具体条件灵活选择.【来源:21·世纪·教育·网】
【关键词】三角形的中位线定理;平行四边形的判定;余角;直角三角形的判定与性质
19.【答案】:(1)见解析(2)图②中:AC+DE=DF;图③中:AC+DF=DE.(3)当如图①的情况,DF=AC-DE=6-4=2;当如图③的情况,DF=AC+DE=6+4=10.2-1-c-n-j-y
【解析】:
(1)证明:∵DF∥AC,DE∥AB,
∴四边形AFDE是平行四边形.
∴AF=DE,
∵DF∥AC,
∴∠FDB=∠C
又∵AB=AC,
∴∠B=∠C,
∴∠FDB=∠B
∴DF=BF
∴DE+DF=AB=AC;
(2)图②中:AC+DE=DF.
图③中:AC+DF=DE.
(3)当如图①的情况,DF=AC-DE=6-4=2;
当如图③的情况,DF=AC+DE=6+4=10.【来源:21cnj*y.co*m】
∴∠AGD=90°,即△AGD是直角三角形。
M
F
A
B
D
C
E
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
〖鲁教版五四制八年级上数学单元测试卷〗
第五章《平行四边形》
(时间:90分钟,总分100分)
题 号 一 二 三 总 分
得 分
班级: 姓名: 考号:
一、选择题(本大题共10小题,每小题3分,满分30分,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分.)21·世纪*教育网
1.一个多边形的内角和是外角和的2倍,这个多边形是( )
A.四边形 B.五边形 C.六边形 D.八边形
2.如图,点E,F是□ABCD对角线上两点,在条件①DE=BF;②∠ADE=∠CBF;③AF=CE; ④∠AEB=∠CFD中,添加一个条件,使四边形DEBF是平行四边形,可添加的条件是( ).
A.①②③ B.①②④ C.①③④ D.②③④
3. 在□ABCD中,对角线AC,BD相交于O,AC=10,BD=8,则AD的长度取值范围是( )
A. AD >0 B. AD>1 C. AD<9 D. 1
A. AB=CD B. EC=FG
C.A,B 两点间的距离就是线段AB的长度
D.a与b的距离就是CD的长度
5. 如图,AB∥CD,E,F分别为AC,BD中点,若AB=5,CD=3,则EF的长为( )
A. 4 B. 3 C.2 D.1
6. 如图,在△ABC中,点D在边BC上,BD=AB,BM⊥AD于点M,N是AC的中点,连接MN.若DC=16 cm,则MN的长为( A )21世纪教育网版权所有21*cnjy*com
A. 8 cm B. 10 cm C. 12 cm D. 14 cm
7.如图,平行四边形ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为 ( )
A.3cm B.4cm C.5m D.8cm
8. 如图,△ABC的面积为16,点D是BC边上一点,且BD=BC,点G是AB上一点,点H在△ABC内部,且四边形BDHG是平行四边形.则图中阴影的面积是( )
A. 3 B. 4 C. 5 D. 6
9.如图,六边形的内角都相等,,则下列结论成立的个数是
① ;②;③;④四边形是平行四边形;⑤六边形 即是中心对称图形,又是轴对称图形( )
A. B. C. D.
10. 如图,在□中,的平分线交于点,交的延长线于点,的平分线交于点,交的延长线于点,与交于点,连接.下列结论错误的是( )2-1-c-n-j-y【版权所有:21教育】
A. B. C. D.
二、填空题(本大题共4小题,每小题4分,满分16分)
11. 如图,A,B是直线m上两个定点,C是直线n上一个动点,且m∥n,以下说法:
①△ABC的周长不变
②△ABC的面积不变
③在中,AB边上的中线长不变
④∠C的度数不变
⑤点C到直线m距离不变
其中正确的有 (填序号)
12. 如图,在四边形ABCD中,AD∥BC,E是BC的中点,AD=5,BC=12,P是BC边上一动点.设PB的长为x,当x的值为____________时,以点P,A,D,E为顶点的四边形是平行四边形.2-1--j-y21*cnjy*com
13. 如图,在中,,,,点、分别是、的中点,交的延长线于。则四边形的面积为 。
14.如图,已知 OABC的顶点A、C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为 .
三、解答题(本大题共6小题,第15、16小题每小题6分,第17、18小题每小题9分,第19、20小题每小题12分,满分54分)
15. (本题满分6分)
如图,在五边形ABCDE中,∠C=100°,∠D=75°,∠E=135°,AP平分∠EAB,BP平分∠ABC,求∠P得度数。
16. (本题满分6分)
已知,如图,平行四边形ABCD中,E是BC边的中点,连DE并延长交AB的延长线于点F,求证:AB=BF. www-2-1-cnjy-com21教育网
17. (本题满分9分)
提出命题:如图,在四边形ABCD中,∠A=∠C,∠ABC=∠ADC,求证:四边形ABCD是平行四边形.21教育名师原创作品
小明提供了如下解答过程:
证明:连接BD.
∵∠1+∠3=180 -∠A,∠2+∠4=180 ―∠C,∠A=∠C,
∴ ∠1+∠3=∠2+∠4.
∵∠ABC=∠ADC,
∴∠1=∠4,∠2=∠3.
∴AB∥CD,AD∥BC.
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).
反思交流:(1)请问小明的解法正确吗?如果有错,说明错在何处,并给出正确的证明过程.
(2)用语言叙述上述命题:___________________________________________________.
运用探究:(3)下列条件中,能确定四边形ABCD是平行四边形的是( )
A. ∠A∶∠B∶∠C∶∠D=1∶2∶3∶4 B. ∠A∶∠B∶∠C∶∠D=1∶3∶1∶3
C. ∠A∶∠B∶∠C∶∠D=2∶3∶3∶2 D. ∠A∶∠B∶∠C∶∠D=1∶1∶3∶3
18. (本题满分9分)
如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
19. (本题满分12分)
在△ABC中,AB=AC,点D在边所在的直线上,过点D作DF∥AC交AB于点F,DE∥AB交直线AC于点E.
(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF= .
20. (本题满分12分)
如图1,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE(不需证明)。
(温馨提示:在图1中,连结BD,取BD的中点H,连结HE、HF,根据三角形中位线定理,证明HE=HF,从而∠1=∠2,再利用平行线性质,可证得∠BME=∠CNE。)
(1)如图2,在四边形ADBC中,AB与CD相交于点O,AB=CD,E、F分别是BC、AD的中点,连结EF,分别交DC、AB于点M、N,判断△OMN的形状,请直接写出结论;
(2)如图3,在△ABC中,AC>AB,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,与BA的延长线交于点G,若∠EFC=60°,连结GD,判断△AGD的形状并证明。
〖鲁教版五四制八年级上数学单元测试卷〗
第五章《平行四边形》答案与解析
1.【答案】:C
【解析】:
解:根据多边形的外角和为360°,可知其内角和为720°,因此可根据多边形的内角和公式(n-2)·180°=720°,解得n=6,故是六边形.
故选:C
考点:多边形的内外角和
2.【答案】: D
【解析】:
解:选D,理由
∵□ABCD
∴AD∥BC
∴∠DAE=∠BCF
∵∠ADE=∠CBF,DE=BF
∴△ADE≌△BCF
∴∠AED=∠CFB
∴∠DEF=∠BFE
DE∥BF
∵∠ADE=∠CBF
∴∠BEF=∠DFE
∴DF∥BE
∴四边形DEBF是平行四边形
故选D
3.【答案】:D
【解析】:
解:如图
∵AC=10,BD=8
∴AO=5,DO=4
∴1
4.【答案】:D
【解析】:解:线段CD与平行线a,b不垂直,a与b的距离不是CD的长度,选项D错误
故选D
6.【答案】:A
【解析】:
解:∵BD=AB,BM⊥AD
∴AM= MD
∵N是AC的中点
∴MN=DC=8
故选A
7.【答案】:B
【解析】:
解:因为四边形ABCD是平行四边形,所以AD=BC.因为□ABCD的周长是26cm,所以AD=BC且AB+BC=13①.因为△AOD的周长比△AOB的周长多3cm,所以AD-AB=3,即BC-AB=3②.①+②,得2BC=16,所以BC=8.因为AC⊥AB,所以∠BAC=90°,又因为E是BC中点,所以AE=BC=×8=4.,故选择B.21世纪教育网版权所有
【解后反思】(1)在直角三角形中出现斜边中点时,一般利用“直角三角形斜边上的中线等于斜边的一半”求斜边上的中线长.(2)平行四边形的性质:对边平行且相等,对角相等,邻角互补,对角线互相平分.www-2-1-cnjy-com
【关键词】平行四边形的性质;直角三角形.
8.【答案】:B
【解析】:
解:设△ABC底边BC上的高为h,△AGH底边GH上的高为h1,△CGH底边GH上的高为h2,则有h=h1+h2.【出处:21教育名师】
S△ABC=BC h=16,
S阴影=S△AGH+S△CGH=GH h1+ GH h2=GH (h1+h2)=GH h.
∵四边形BDHG是平行四边形,且BD=BC,
∴GH=BD=BC.
∴S阴影= ×(BC h)= S△ABC=4.故选择B
【解后反思】具有整体思想,发现两阴影面积的高的和与△ABC的高的关系是解题关键.
【关键词】三角形的面积,平行四边形的性质,整体思想
9.【答案】:D
【解析】:
考点:1.平行四边形的判定和性质;2.平行线的判定和性质;3.轴对称图形;4.中心对称图形.
10.【答案】:D
【解析】:
解:∵四边形ABCD是平行四边形,
∴AH∥BG,AD=BC,
∴∠H=∠HBG,
∵∠HBG=∠HBA,
∴∠H=∠HBA,
∴AH=AB,同理可证BG=AB,
考点:1、平行四边形的性质,2、等腰三角形的判定和性质
二、填空题
11.【答案】:②⑤
【解析】:
解:②△ABC的底边AB不变,高是两平行线m,n之间距离不变,所以面积不变,此选项正确;
⑤点C到直线m距离是两平行线m,n之间距离,所以点C到直线m距离不变
故答案是②⑤
12.【答案】:11或3
【解析】:
解:∵E是BC的中点,BC=12
∴BE=6
分类讨论
①当P点运到到P1时
∵四边形PADE是平行四边形
∴P1E=AD=5
∴PB=x=3
②当P点运到到P2时
∵四边形EADP是平行四边形
∴P2E=AD=5
∴PB=x=11
综上所述:x=11或3
13.【答案】:12
【解析】:
解:∵,,,
∴BC=
∵点是的中点
∴BD=BC=
∵点、分别是、的中点
∴AD∥BF
∵
∴四边形FBDA是平行四边形
过A点作AG⊥BC
∵S△ABC=AB· AC=AG· BC
∴4×6=AG×
∴AG=
∴四边形的面积为:×=12
14.【答案】:5
【解析】:
解:当B在x轴上时,对角线OB长的最小,如图所示:直线x=1与x轴交于点D,直线x=4与x轴交于点E,21cnjy.com
根据题意得:∠ADO=∠CEB=90°,OD=1,OE=4,
∵四边形ABCD是平行四边形,
∴OA∥BC,OA=BC,
∴∠AOD=∠CBE,
在△AOD和△CBE中,
,
∴△AOD≌△CBE(AAS),
∴OD=BE=1,
∴OB=OE+BE=5;
故答案为:5.
三、解答题
15.【答案】:65°
【解析】:解:在五边形ABCDE中
∠C+∠D+∠E+∠EAB+∠ABC=540°
∵∠C=100°,∠D=75°,∠E=135°
∴∠EAB+∠ABC=230°
∵AP平分∠EAB,BP平分∠ABC
∴∠PAB+∠PBC=115°
∴∠P=65°
16.【答案】:证明见解析.
【解析】:1-c-n-j-y
证明:∵E是BC的中点,
∴CE=BE,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠DCB=∠FBE,
在△CED和△BEF中,
,
∴△CED≌△BEF(ASA),
∴CD=BF,
∴AB=BF.
考点:1.平行四边形的性质;2.全等三角形的判定与性质.
17.【答案】:
【解析】:
解:(1)小明的解法不正确,错在推出∠1+∠3=∠2+∠4后,由∠ABC=∠ADC,不能直接推出∠1=∠4,∠2=∠3.21·cn·jy·com
正确证明:因为∠A+∠ABC+∠C+∠ADC=360°,∠A=∠C,∠ABC=∠ADC,所以2∠A+
2∠ABC=360°.所以∠A+∠ABC=180°.所以AD∥BC.同理∠A+∠ADC=180°.所以AB∥CD.所以四边形ABCD是平行四边形.www.21-cn-jy.com
(2)两组对角分别相等的四边形是平行四边形
(3)B
18.【答案】:(1)见解析;(2)6
【解析】:
解:(1)证明:∵点D、E、F、G分别为线段AB、OB、OC、AC的中点,
∴DG为△ABC的中位线,EF为△OBC的中位线,
∴DG∥BC且DG=BC,EF∥BC且EF=BC,
∴DG∥EF,DG=EF,∴四边形DEFG是平行四边形.
(2)解:∵∠OBC和∠OCB互余,∴△OBC是直角三角形,∠BOC=90°.
∵M为EF的中点,∴OM为Rt△OEF斜边的中线,
∴EF=2OM=2×3=6,∴DG=EF=6.
【解后反思】(1)当两个三角形有一条公共边时,则它们所对的三角形的中位线相等且平行.当两个直角三角形有公共的斜边时,则它们斜边上的中线相等.2·1·c·n·j·y
(2)平行四边形的判定方法,可分别从边、角、对角线等不同角度去理解与记忆,应用时可根据具体条件灵活选择.【来源:21·世纪·教育·网】
【关键词】三角形的中位线定理;平行四边形的判定;余角;直角三角形的判定与性质
19.【答案】:(1)见解析(2)图②中:AC+DE=DF;图③中:AC+DF=DE.(3)当如图①的情况,DF=AC-DE=6-4=2;当如图③的情况,DF=AC+DE=6+4=10.2-1-c-n-j-y
【解析】:
(1)证明:∵DF∥AC,DE∥AB,
∴四边形AFDE是平行四边形.
∴AF=DE,
∵DF∥AC,
∴∠FDB=∠C
又∵AB=AC,
∴∠B=∠C,
∴∠FDB=∠B
∴DF=BF
∴DE+DF=AB=AC;
(2)图②中:AC+DE=DF.
图③中:AC+DF=DE.
(3)当如图①的情况,DF=AC-DE=6-4=2;
当如图③的情况,DF=AC+DE=6+4=10.【来源:21cnj*y.co*m】
∴∠AGD=90°,即△AGD是直角三角形。
M
F
A
B
D
C
E
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
