西师大版小学六年级数学上 2.5解决与圆有关的实际问题课件
文档属性
| 名称 | 西师大版小学六年级数学上 2.5解决与圆有关的实际问题课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-10 00:00:00 | ||
图片预览





文档简介
课件29张PPT。六年级 数学 上册西师大版第2单元 圆5 解决与圆有关的
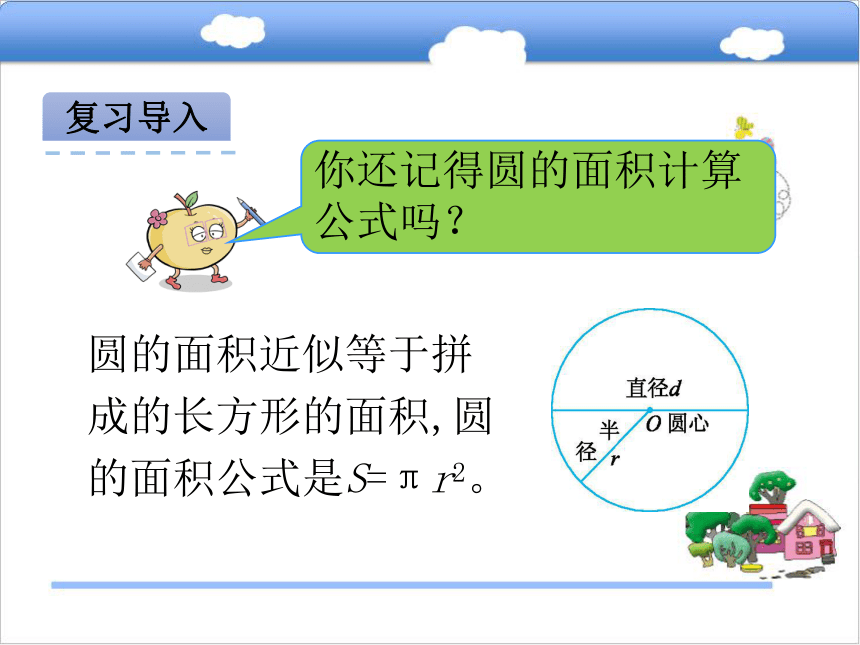
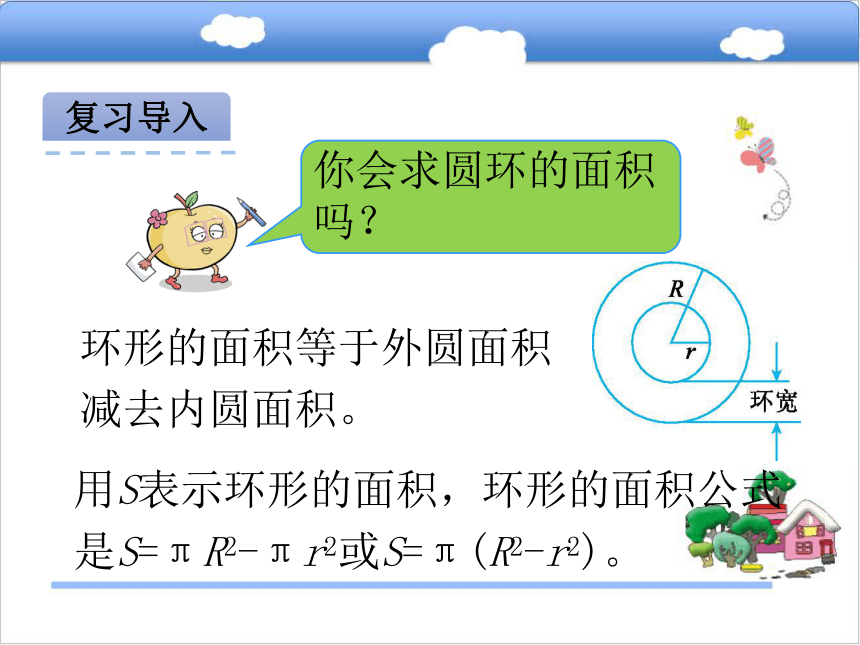
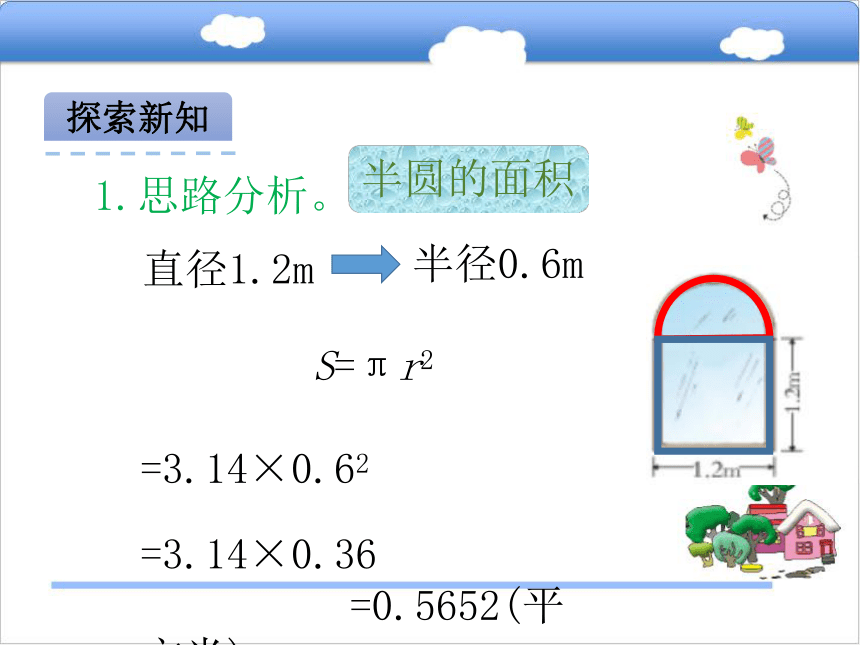
实际问题学习目标1.会运用圆的面积公式解决有关问题。2.会用“切割法”“平移法”等方法求组合图形的面积。3.初步了解“图形结合”的思想。复习导入圆的面积近似等于拼成的长方形的面积,圆的面积公式是S=πr2。复习导入环形的面积等于外圆面积减去内圆面积。用S表示环形的面积,环形的面积公式是S=πR2-πr2或S=π(R2-r2)。情景导入1学校阅览室的窗户上面是半圆,下面是正方形(如下图)。窗户的面积约是多少平方米?(得数保留整数)探索新知1.思路分析。半圆的面积直径1.2m半径0.6m S=πr2
=3.14×0.62
=3.14×0.36
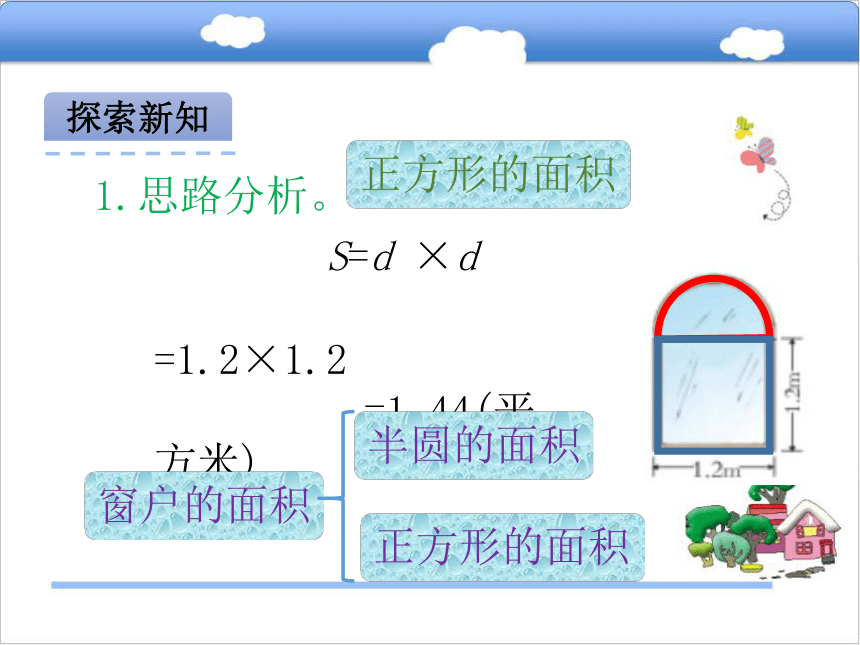
=0.5652(平方米)探索新知1.思路分析。正方形的面积 S=d ×d
=1.2×1.2
=1.44(平方米)窗户的面积半圆的面积正方形的面积探索新知2.解决问题。窗户的面积?解:答:窗户的面积约是2平方米。一张可折叠的圆桌,半径是0.6米,折叠后成了正方形。折叠部分的面积约是多少平方米?(得数保留两位小数)情景导入2探索新知折叠部分的面积解决问题:圆的面积=-正方形的面积圆的面积:S=πr2
=3.14×0.62
=3.14×0.36
=1.1304(平方米)探索新知解决问题:正方形的面积:
0.6×1.2÷2×2
=0.72(平方米)折叠部分的面积:
1.1304-0.72=0.4104
≈0.41(平方米)答:折叠部分的面积约是0.41平方米。典题精讲求下面涂色部分的面积。思路分析:
圆的面积半圆的面积三角形的面积涂色部分的面积S1=πr2?S2=ah÷2S=S1-S2典题精讲求下面涂色部分的面积。解决问题:
解:圆的半径:r=d÷2=10÷2=5(分米)
圆的面积:S=πr2=3.14×52
=78.5(平方分米)
半圆的面积:S÷2=78.5÷2
=39.25(平方分米)典题精讲求下面涂色部分的面积。解决问题:
涂色部分的面积:
39.25-25=14.25(平方分米)答:涂色部分的面积是14.25平方厘米。三角形的面积:S=a×r÷2=10×5÷2=25(平方分米)一个环形铁片,内圆半径是6厘米,外圆半径是10厘米。这个环形铁片的面积是多少平方厘米?错误解答易错提醒解: S=πr2
=3.14×62
=113.04(平方厘米)答:这个环形铁片的面积是113.04平方厘米。一个环形铁片,内圆半径是6厘米,外圆半径是10厘米。这个环形铁片的面积是多少平方厘米?易错提醒错误原因:错在直接用圆周率去乘内圆半径的平方了,没有掌握环形面积的求法。易错提醒要求环形的面积,应该用外圆的面积减去内圆的面积。如果用R表示外圆的半径,r表示内圆的半径,那么环形的面积就是πR2-πr2,也可以利用乘法分配律,将计算公式表示为S=π(R2-r2)。一个环形铁片,内圆半径是6厘米,外圆半径是10厘米。这个环形铁片的面积是多少平方厘米?正确解答易错提醒解: 3.14×(102-62) =3.14×64 =200.96(平方厘米)答:这个环形铁片的面积是200.96平方厘米。学以致用1.计算下面涂色部分的面积。(单位:米)
解: 3.14×(72-42) =3.14×33 =103.62(平方米)涂色部分的面积外圆的面积=-内圆的面积答:涂色部分的面积是103.62平方米。学以致用2.有一个运动场,两端是半圆,中间是长方形。它的周长和面积各是多少?解:周长=长方形两条长+圆的周长
C=100×2+3.14×64
=400.96(米) 学以致用2.有一个运动场,两端是半圆,中间是长方形。它的周长和面积各是多少?解:面积=长方形面积+圆的面积
S=100×64+3.14×(64÷2)2
=9615.36(平方米) 学以致用3.求阴影部分的面积。?圆的面积合起来就是一个整圆学以致用3.求阴影部分的面积。解:S=πr2
=3.14×42
=3.14×16
=50.24(cm2)答:阴影部分的面积是50.24cm2。学以致用4.如图,大、小两个正方形的边长分别是大、小两个圆的半径。阴影部分的面积是10平方厘米。求圆环的面积。圆环的面积外圆面积=-内圆面积解题思路:大圆半径(也就是大正方形的边长)为R小圆半径(也就是小正方形的边长)为rRr学以致用解题思路:大圆半径(也就是大正方形的边长)为R小圆半径(也就是小正方形的边长)为rRr大正方形的面积为R2小正方形的面积为r2阴影部分的面积是10平方厘米R2-r2=10(平方厘米)学以致用4.如图,大、小两个正方形的边长分别是大、小两个圆的半径。阴影部分的面积是10平方厘米。求圆环的面积。圆环的面积外圆面积=-内圆面积解:Rr 3.14×R2-3.14×r2
=3.14×(R2-r2)
=3.14×10
=31.4(平方厘米)答:圆环的面积是31.4平方厘米。课堂小结求两个或两个以上组合图形的面积时,先要分清组合图形是由哪几个规则图形组成的,求出各个规则图形的面积后,再相加(减)即可;
求不规则图形的面积时,可以考虑不规则图形是由哪几个规则图形组成的。谢谢
实际问题学习目标1.会运用圆的面积公式解决有关问题。2.会用“切割法”“平移法”等方法求组合图形的面积。3.初步了解“图形结合”的思想。复习导入圆的面积近似等于拼成的长方形的面积,圆的面积公式是S=πr2。复习导入环形的面积等于外圆面积减去内圆面积。用S表示环形的面积,环形的面积公式是S=πR2-πr2或S=π(R2-r2)。情景导入1学校阅览室的窗户上面是半圆,下面是正方形(如下图)。窗户的面积约是多少平方米?(得数保留整数)探索新知1.思路分析。半圆的面积直径1.2m半径0.6m S=πr2
=3.14×0.62
=3.14×0.36
=0.5652(平方米)探索新知1.思路分析。正方形的面积 S=d ×d
=1.2×1.2
=1.44(平方米)窗户的面积半圆的面积正方形的面积探索新知2.解决问题。窗户的面积?解:答:窗户的面积约是2平方米。一张可折叠的圆桌,半径是0.6米,折叠后成了正方形。折叠部分的面积约是多少平方米?(得数保留两位小数)情景导入2探索新知折叠部分的面积解决问题:圆的面积=-正方形的面积圆的面积:S=πr2
=3.14×0.62
=3.14×0.36
=1.1304(平方米)探索新知解决问题:正方形的面积:
0.6×1.2÷2×2
=0.72(平方米)折叠部分的面积:
1.1304-0.72=0.4104
≈0.41(平方米)答:折叠部分的面积约是0.41平方米。典题精讲求下面涂色部分的面积。思路分析:
圆的面积半圆的面积三角形的面积涂色部分的面积S1=πr2?S2=ah÷2S=S1-S2典题精讲求下面涂色部分的面积。解决问题:
解:圆的半径:r=d÷2=10÷2=5(分米)
圆的面积:S=πr2=3.14×52
=78.5(平方分米)
半圆的面积:S÷2=78.5÷2
=39.25(平方分米)典题精讲求下面涂色部分的面积。解决问题:
涂色部分的面积:
39.25-25=14.25(平方分米)答:涂色部分的面积是14.25平方厘米。三角形的面积:S=a×r÷2=10×5÷2=25(平方分米)一个环形铁片,内圆半径是6厘米,外圆半径是10厘米。这个环形铁片的面积是多少平方厘米?错误解答易错提醒解: S=πr2
=3.14×62
=113.04(平方厘米)答:这个环形铁片的面积是113.04平方厘米。一个环形铁片,内圆半径是6厘米,外圆半径是10厘米。这个环形铁片的面积是多少平方厘米?易错提醒错误原因:错在直接用圆周率去乘内圆半径的平方了,没有掌握环形面积的求法。易错提醒要求环形的面积,应该用外圆的面积减去内圆的面积。如果用R表示外圆的半径,r表示内圆的半径,那么环形的面积就是πR2-πr2,也可以利用乘法分配律,将计算公式表示为S=π(R2-r2)。一个环形铁片,内圆半径是6厘米,外圆半径是10厘米。这个环形铁片的面积是多少平方厘米?正确解答易错提醒解: 3.14×(102-62) =3.14×64 =200.96(平方厘米)答:这个环形铁片的面积是200.96平方厘米。学以致用1.计算下面涂色部分的面积。(单位:米)
解: 3.14×(72-42) =3.14×33 =103.62(平方米)涂色部分的面积外圆的面积=-内圆的面积答:涂色部分的面积是103.62平方米。学以致用2.有一个运动场,两端是半圆,中间是长方形。它的周长和面积各是多少?解:周长=长方形两条长+圆的周长
C=100×2+3.14×64
=400.96(米) 学以致用2.有一个运动场,两端是半圆,中间是长方形。它的周长和面积各是多少?解:面积=长方形面积+圆的面积
S=100×64+3.14×(64÷2)2
=9615.36(平方米) 学以致用3.求阴影部分的面积。?圆的面积合起来就是一个整圆学以致用3.求阴影部分的面积。解:S=πr2
=3.14×42
=3.14×16
=50.24(cm2)答:阴影部分的面积是50.24cm2。学以致用4.如图,大、小两个正方形的边长分别是大、小两个圆的半径。阴影部分的面积是10平方厘米。求圆环的面积。圆环的面积外圆面积=-内圆面积解题思路:大圆半径(也就是大正方形的边长)为R小圆半径(也就是小正方形的边长)为rRr学以致用解题思路:大圆半径(也就是大正方形的边长)为R小圆半径(也就是小正方形的边长)为rRr大正方形的面积为R2小正方形的面积为r2阴影部分的面积是10平方厘米R2-r2=10(平方厘米)学以致用4.如图,大、小两个正方形的边长分别是大、小两个圆的半径。阴影部分的面积是10平方厘米。求圆环的面积。圆环的面积外圆面积=-内圆面积解:Rr 3.14×R2-3.14×r2
=3.14×(R2-r2)
=3.14×10
=31.4(平方厘米)答:圆环的面积是31.4平方厘米。课堂小结求两个或两个以上组合图形的面积时,先要分清组合图形是由哪几个规则图形组成的,求出各个规则图形的面积后,再相加(减)即可;
求不规则图形的面积时,可以考虑不规则图形是由哪几个规则图形组成的。谢谢
