13.3.2(第5课时) 巧用特殊角构造含30°角的直角三角形课件
文档属性
| 名称 | 13.3.2(第5课时) 巧用特殊角构造含30°角的直角三角形课件 |  | |
| 格式 | zip | ||
| 文件大小 | 211.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-11 20:19:10 | ||
图片预览




文档简介
课件16张PPT。第十三章 轴对称第5课时 巧用特殊角构造含30°
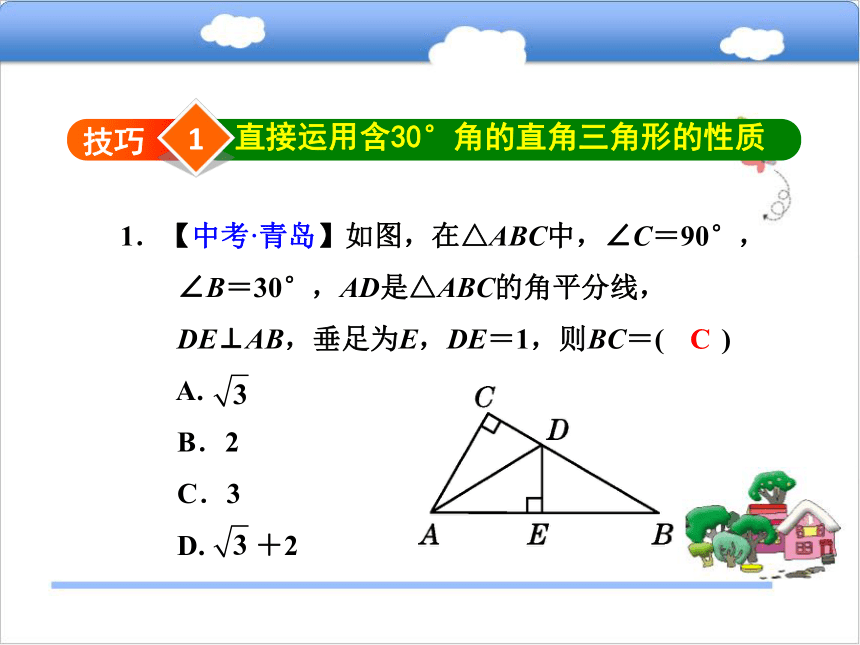
角的直角三角形名师点金 在解决有关三角形的问题时,遇到含有120°角的等腰三角形或含有30°角的三角形时,常常通过连线,延长或作垂线的方式,构造含30°角的直角三角形,将角的关系转化为边的关系来解决问题.1技巧直接运用含30°角的直角三角形的性质1.【中考·青岛】如图,在△ABC中,∠C=90°,
∠B=30°,AD是△ABC的角平分线,
DE⊥AB,垂足为E,DE=1,则BC=( )
A.
B.2
C.3
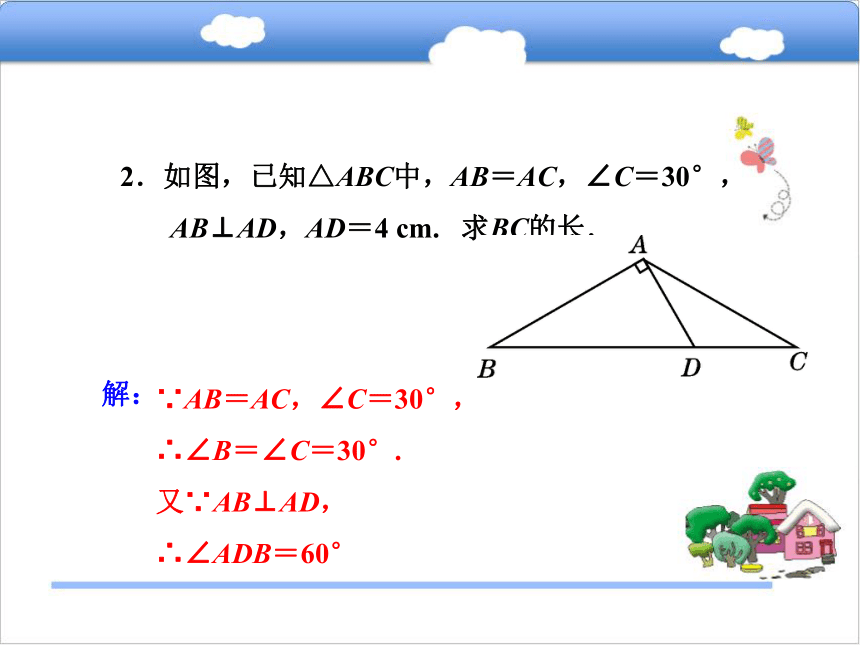
D. +2C2.如图,已知△ABC中,AB=AC,∠C=30°,
AB⊥AD,AD=4 cm. 求BC的长.∵AB=AC,∠C=30°,
∴∠B=∠C=30°.
又∵AB⊥AD,
∴∠ADB=60°解:∵∠ADB=∠C+∠CAD.
∴∠CAD=30°=∠C.
∴CD=AD=4 cm.
∵AB⊥AD,∠B=30°,
∴BD=2AD=8 cm.
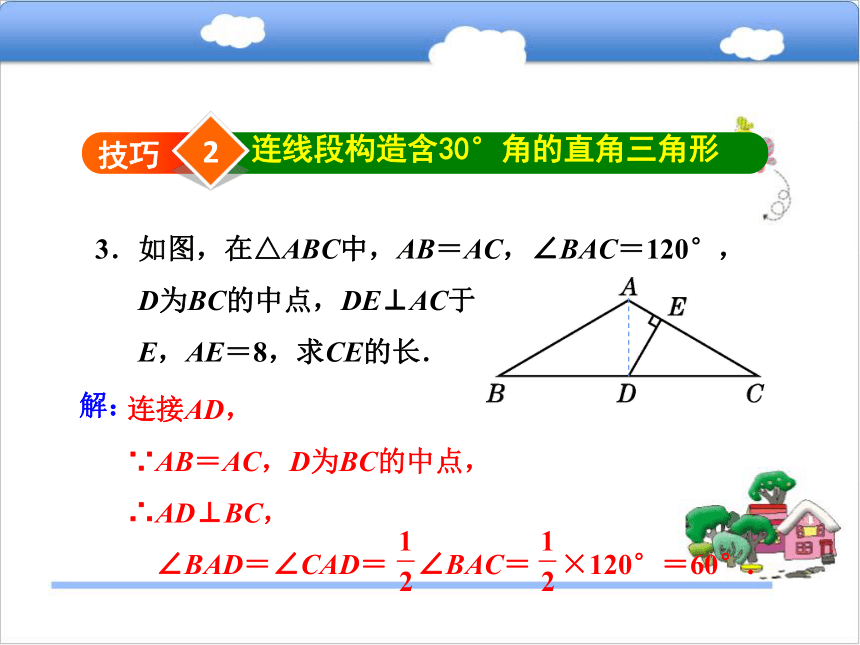
∴BC=BD+CD=12 cm.2连线段构造含30°角的直角三角形技巧3.如图,在△ABC中,AB=AC,∠BAC=120°,
D为BC的中点,DE⊥AC于
E,AE=8,求CE的长.连接AD,
∵AB=AC,D为BC的中点,
∴AD⊥BC,
∠BAD=∠CAD= ∠BAC= ×120°=60°.解:在Rt△ADE中,∠CAD=60°,
∴∠ADE=30°,
∴AD=2AE=16.
在△ABC中,AB=AC,∠BAC=120°.
∴∠B=∠C=30°,
∴AC=2AD=2×16=32.
∴CE=AC-AE=32-8=24.4.如图,已知在△ABC中,AB=AC,∠A=
120°,DE垂直平分AB于点D,交BC于点
E,求证:CE=2BE. 如图,连接AE.
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°.
∵DE垂直平分AB,
∴BE=AE.
∴∠BAE=∠B=30°.
∴∠EAC=120°-30°=90°.
又∵∠C=30°,∴CE=2AE.
又∵BE=AE,∴CE=2BE.证明:3延长两边构造含30°角的直角三角形技巧5.如图,在四边形ABCD中,AD=4,BC=1,
∠A=30°,∠B=90°,∠ADC=120°,
求CD的长.延长AD,BC交于点E.
∵∠A=30°,∠B=90°,
∴∠E=60°.解:又∵∠ADC=120°,
∴∠EDC=180°-120°=60°.
∴△DCE是等边三角形.
设CD=CE=DE=a,则有2(1+a)=4+a,
解得a=2.
∴CD的长为2.4作垂线构造含30°角的直角三角形6.如图,在四边形ABCD中,∠B=90°,DC∥AB,
AC平分∠BAD,∠DAB=30°,
求证:AD=2BC.技巧过点C作CE⊥AD,
交AD的延长线于E.
∵AC平分∠BAD,∠DAB=30°.
∴∠BAC=∠EAC=15°.证明:又∵DC∥AB,
∴∠DCA=∠BAC=15°.
∴∠DCA=∠EAC.
∴AD=CD.
在△DEC中,∠EDC=30°,∠DEC=90°,
∴CD=2CE.
∵AC平分∠BAD,CE⊥AE,CB⊥AB,
∴CE=BC,∴AD=2BC.7.如图,在△ABC中,BD=DC,若AD⊥AC,
∠BAD=30°.求证:AC= AB.过点B作BE⊥AD交AD的延
长线于E,则∠AEB=90°.
∵∠BAD=30°,
∴BE= AB.证明:∵AD⊥AC,∴∠DAC=90°,
∴∠AEB=∠DAC.
又∵BD=CD,∠BDE=∠CDA,
∴△BED≌△CAD,
∴BE=AC,
∴AC= AB.由结论AC= AB和条件∠BAD=30°,就想到能否找到或构造直角三角形,而显然图中没有含30°角的直角三角形,所以过点B作BE⊥AD交AD的延长线于点E,这样就得到了直角三角形ABE,这是解决本题的关键.点拨:
角的直角三角形名师点金 在解决有关三角形的问题时,遇到含有120°角的等腰三角形或含有30°角的三角形时,常常通过连线,延长或作垂线的方式,构造含30°角的直角三角形,将角的关系转化为边的关系来解决问题.1技巧直接运用含30°角的直角三角形的性质1.【中考·青岛】如图,在△ABC中,∠C=90°,
∠B=30°,AD是△ABC的角平分线,
DE⊥AB,垂足为E,DE=1,则BC=( )
A.
B.2
C.3
D. +2C2.如图,已知△ABC中,AB=AC,∠C=30°,
AB⊥AD,AD=4 cm. 求BC的长.∵AB=AC,∠C=30°,
∴∠B=∠C=30°.
又∵AB⊥AD,
∴∠ADB=60°解:∵∠ADB=∠C+∠CAD.
∴∠CAD=30°=∠C.
∴CD=AD=4 cm.
∵AB⊥AD,∠B=30°,
∴BD=2AD=8 cm.
∴BC=BD+CD=12 cm.2连线段构造含30°角的直角三角形技巧3.如图,在△ABC中,AB=AC,∠BAC=120°,
D为BC的中点,DE⊥AC于
E,AE=8,求CE的长.连接AD,
∵AB=AC,D为BC的中点,
∴AD⊥BC,
∠BAD=∠CAD= ∠BAC= ×120°=60°.解:在Rt△ADE中,∠CAD=60°,
∴∠ADE=30°,
∴AD=2AE=16.
在△ABC中,AB=AC,∠BAC=120°.
∴∠B=∠C=30°,
∴AC=2AD=2×16=32.
∴CE=AC-AE=32-8=24.4.如图,已知在△ABC中,AB=AC,∠A=
120°,DE垂直平分AB于点D,交BC于点
E,求证:CE=2BE. 如图,连接AE.
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°.
∵DE垂直平分AB,
∴BE=AE.
∴∠BAE=∠B=30°.
∴∠EAC=120°-30°=90°.
又∵∠C=30°,∴CE=2AE.
又∵BE=AE,∴CE=2BE.证明:3延长两边构造含30°角的直角三角形技巧5.如图,在四边形ABCD中,AD=4,BC=1,
∠A=30°,∠B=90°,∠ADC=120°,
求CD的长.延长AD,BC交于点E.
∵∠A=30°,∠B=90°,
∴∠E=60°.解:又∵∠ADC=120°,
∴∠EDC=180°-120°=60°.
∴△DCE是等边三角形.
设CD=CE=DE=a,则有2(1+a)=4+a,
解得a=2.
∴CD的长为2.4作垂线构造含30°角的直角三角形6.如图,在四边形ABCD中,∠B=90°,DC∥AB,
AC平分∠BAD,∠DAB=30°,
求证:AD=2BC.技巧过点C作CE⊥AD,
交AD的延长线于E.
∵AC平分∠BAD,∠DAB=30°.
∴∠BAC=∠EAC=15°.证明:又∵DC∥AB,
∴∠DCA=∠BAC=15°.
∴∠DCA=∠EAC.
∴AD=CD.
在△DEC中,∠EDC=30°,∠DEC=90°,
∴CD=2CE.
∵AC平分∠BAD,CE⊥AE,CB⊥AB,
∴CE=BC,∴AD=2BC.7.如图,在△ABC中,BD=DC,若AD⊥AC,
∠BAD=30°.求证:AC= AB.过点B作BE⊥AD交AD的延
长线于E,则∠AEB=90°.
∵∠BAD=30°,
∴BE= AB.证明:∵AD⊥AC,∴∠DAC=90°,
∴∠AEB=∠DAC.
又∵BD=CD,∠BDE=∠CDA,
∴△BED≌△CAD,
∴BE=AC,
∴AC= AB.由结论AC= AB和条件∠BAD=30°,就想到能否找到或构造直角三角形,而显然图中没有含30°角的直角三角形,所以过点B作BE⊥AD交AD的延长线于点E,这样就得到了直角三角形ABE,这是解决本题的关键.点拨:
