数学北师大版七上第三章整式及其加减 练习题(有答案)
文档属性
| 名称 | 数学北师大版七上第三章整式及其加减 练习题(有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 409.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-12 21:25:27 | ||
图片预览




文档简介
第三章 整式及其加减
3.1 字母表示数
基础题
知识点 用字母表示数
1.教室内有m排座位,每排有n个座位,则这个教室共有座位(A)
A.mn个
B.(m+n)个
C.(m-n)个
D.(2m+2n)个
2.某日的温差为9
℃,最高温度为t
℃,则最低气温可表示为(A)
A.(t-9)℃
B.(9-t)℃
C.(-9-t)℃
D.(t+9)℃
3.(吉林中考)小红要购买珠子串成一条手链.黑色珠子每个a元,白色珠子每个b元,要串成如图所示的手链,小红购买珠子应该花费(A)
A.(3a+4b)元
B.(4a+3b)元
C.4
(a+b)元
D.3
(a+b)元
4.用含字母的式子表示:
(1)x与y两数的差的平方:(x-y)2;
(2)a与b的平方差:a2-b2.
5.小明从每月的零花钱中储存x元钱捐给希望工程,一年下来小明捐款12x元.
6.今年,和你一起升入初中的同学约有15万人,其中男生约有a万人,则女生约有(15-a)万人.
中档题
7.车上有100袋面粉,每袋50千克,取下x袋,车上还有面粉(A)
A.50(100-x)千克
B.(50×100-x)千克
C.100(50-x)千克
D.50x千克
8.张老板以每个a元的单价买进水蜜桃100个,现以每个比单价多20%的价格卖出70个后,再以每个比单价低b元的价格将剩下的30个卖出,则全部水蜜桃共卖(D)
A.[70a+30(a-b)]元
B.[70(1+20%)a+30b]元
C.[100(1+20%)a-30(a-b)]元
D.[70(1+20%)a+30(a-b)]元
9.今年五月份,由于禽流感的影响,某市鸡肉的价格下降了10%,设鸡肉原来的价格为a元/千克,则五月份的价格为0.9a元/千克.
10.10名学生的平均成绩是x,如果另外5名学生每人得84分,那么整个组的平均成绩是分.
11.用字母表示图中阴影部分的面积.
(1)
(2)
解:(1)阴影部分的面积为ab-bx.
(2)阴影部分的面积为R2-πR2.
综合题
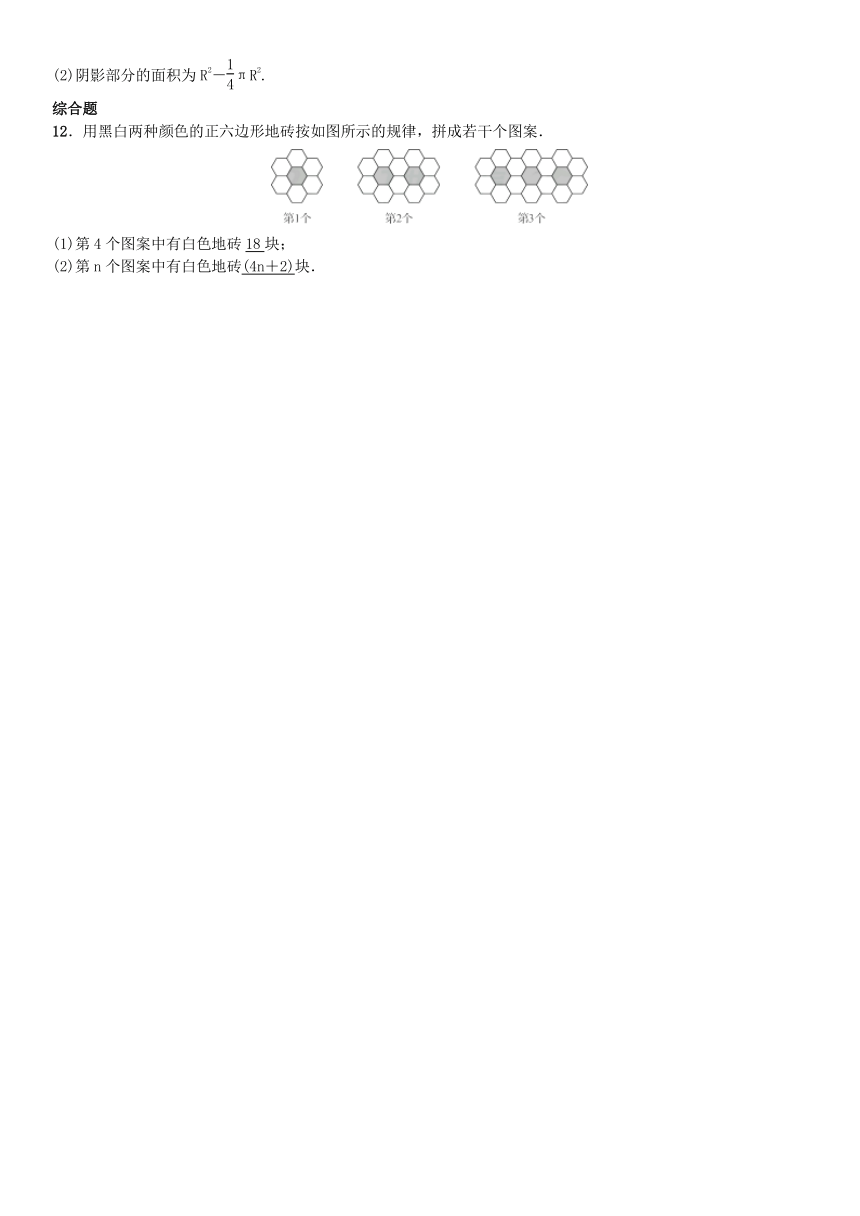
12.用黑白两种颜色的正六边形地砖按如图所示的规律,拼成若干个图案.
(1)第4个图案中有白色地砖18块;
(2)第n个图案中有白色地砖(4n+2)块.
3.2 代数式
第1课时 代数式
基础题
知识点1 代数式的概念
1.在a,0,π,,0.2xyz,n-3,-中,代数式的个数是(D)
A.4
B.5
C.6
D.7
知识点2 代数式的意义
2.在下列表述中,不能表示代数式“4a”意义的是(D)
A.4的a倍
B.a的4倍
C.4个a相加
D.4个a相乘
3.实验中学初三年级12个班总共有团员a人,则表示的实际意义是实验中学初三年级平均每班的团员的人数.
4.联系实际背景,说明代数式6a2的意义.
解:答案不唯一,如:6个边长为a的正方形的面积.
知识点3 列代数式
5.x的2倍与y的和的平方用代数式表示为(A)
A.(2x+y)2
B.2x+y2
C.2x2+y2
D.2(x+y)2
6.3月12日某班50名学生到郊外植树,平均每人植树a棵,则该班一共植树50a棵.
7.某种苹果的售价是每千克x元,用面值为100元的人民币购买了5千克,应找回(100-5x)元.
8.小明的存款是a元,小华的存款比小明存款的一半多2元,则小华存款为(a+2)元.
中档题
9.下列语句正确的是(B)
A.1+a不是一个代数式
B.0是代数式
C.S=πr2是一个代数式
D.单独一个字母a不是代数式
10.a表示一个一位数,b表示一个两位数,把a放到b的左边组成一个三位数,则这个三位数可以表示为(C)
A.ab
B.10a+b
C.100a+b
D.a+b
11.一批产品,甲单独做a小时可以完成,乙单独做b小时可以完成,现在已完成了任务的+,则甲、乙的工作情况是甲已工作了2小时,乙已工作了5小时.
12.A、B两地相距150千米,李明驾驶汽车以v千米/小时的速度从A地驶往B地,请你用代数式表示:
(1)李明从A地到B地需要的时间;
(2)如果汽车每小时多行驶10千米,李明从A地到B地需要多长时间?
(3)在(2)的情况下,李明从A地到B地比原计划少用的时间是多少?
解:(1)小时.
(2)小时.
(3)(-)小时.
综合题
13.家家乐超市出售一种商品,其原价为a元,现有三种调价方案:
①先提价20%,再降价20%;②先降价20%,再提价20%;③先提价15%,再降价15%.
(1)问用这三种方案调价结果是否一样?
(2)最后是不是都恢复了原价?
解:(1)①(1+20%)(1-20%)a=0.96a;
②(1-20%)(1+20%)a=0.96a;
③(1+15%)(1-15%)a=0.977
5a.
前两种方案调价结果一样.
(2)这三种方案最后的价格与原价都不一致.
第2课时 代数式值的变化
基础题
知识点1 求代数式的值
1.已知x=1,y=2,则代数式x-y的值为(B)
A.1
B.-1
C.2
D.-3
2.当a=3,b=2时,a2+2ab+b2的值是(D)
A.5
B.13
C.21
D.25
3.当a=2时,代数式3a-1的值是5.
4.当x=-2,y=3时,代数式2x2-3y的值是-1.
知识点2 数值转换机
5.如图是一个数值转换机,输入x,输出3(x-2),下面给出了四种转换步骤,其中不正确的是(C)
A.先减去2,再乘以3
B.先加上-2,再乘以3
C.先乘以3,再减去2
D.先乘以3,再减去6
6.按照如图所示的程序计算当x分别为-3,0时的输出值.
解:程序对应的代数式为2(5x-2).
当x=-3时,2(5x-2)=2×[5×(-3)-2]=2×(-17)=-34;
当x=0时,2(5x-2)=2×(5×0-2)=-4.
知识点3 代数式的值的简单应用
7.人们通常用c表示摄氏温度(℃),f表示华氏温度(?),c与f之间的关系为c=(f-32),当华氏温度为59(?)时,摄氏温度为(B)
A.-15
℃
B.15
℃
C.112.6
℃
D.95.8
℃
8.在三角形的面积公式S=ah中,a表示底边长,h表示底边上的高,若a=3.2
cm,h=5
cm,则S=8cm2.
中档题
9.下列说法正确的有(A)
①代数式的值只与代数式本身有关;②一个含有字母的代数式,只有一个值;③代数式x2+x-1的值为-1.
A.0个
B.1个
C.2个
D.3个
10.根据流程图中的程序,当输入数值x为-2时,输出数值y为(B)
A.4
B.6
C.8
D.10
11.当x=7与x=-7时,代数式3x4-2x2+1的两个值(A)
A.相等
B.互为倒数
C.互为相反数
D.既不相等也不互为相反数
12.已知2x-5y3=3,则9-4(2x-5y3)的值是-3.
13.某商店出售一批水果,最初以每箱a元的价格出售m箱,后来每箱降价为b元,又售出m箱,剩下30箱又以每箱再降价5元出售.
(1)用代数式表示这批水果共售多少元?
(2)如果a=20,b=18,m=60,进这批水果共花去1
500元,那么该商店赚了多少元?
解:(1)[am+bm+30(b-5)]元.
(2)1
170元.
3.3 整式
基础题
知识点1 单项式及其有关概念
1.在,x+1,-2,-,0.72xy,,各式中,单项式的个数是(C)
A.2
B.3
C.4
D.5
2.(台州中考)单项式2a的系数是(A)
A.2
B.2a
C.1
D.a
3.(德宏中考)-4a2b的次数是(A)
A.3
B.2
C.4
D.-4
4.写出下列各单项式的系数和次数:
单项式
y
-x3
ab2c3
-
πr2
系数
1
-1
1
-
π
次数
1
3
6
3
2
知识点2 多项式及其有关概念
5.下列式子:a+2b,,(x2-y2),,0中,多项式的个数是(B)
A.2
B.3
C.4
D.5
6.多项式3x2-2x-1的各项分别是(D)
A.3x2,2x,1
B.3x2,-2x,1
C.-3x2,2x,-1
D.3x2,-2x,-1
7.如果xn+x2-1是五次多项式,那么n的值是(C)
A.3
B.4
C.5
D.6
8.(佛山中考)多项式2a2b-a2b-ab的项数及次数分别是(A)
A.3,3
B.3,2
C.2,3
D.2,2
9.多项式x+3x2-53的次数最高的项是3x2,一次项系数是,常数项是-53,它是二次三项式.
10.一个关于x的多项式,一次项系数是1,二次项系数和常数项都是-,则这个多项式是-x2+x-.
11.填表:
多项式
3a-1
-x+5x2+7
-2x2y+6xy4-3
各项
3a,-1
-x,5x2,7
-2x2y,6xy4,-3
次数
1
2
5
最高次项
3a
5x2
6xy4
几次几项式
一次二项式
二次三项式
五次三项式
知识点3 整式的概念
12.在代数式x2+5,-1,-3x+2,π,,x2+,5x中,整式有(C)
A.3个
B.4个
C.5个
D.6个
中档题
13.下列说法中正确的是(B)
A.是单项式
B.单项式可以看成是只有一项的多项式
C.单项式3(x2+1)的系数是3
D.多项式的常数项
14.如果一个多项式是四次多项式,那么它任何一项的次数(D)
A.都小于4
B.都等于4
C.都不小于4
D.都不大于4
15.(3m-2)x2yn+1是关于x,y的五次单项式,且系数为1,则m,n的值分别是(B)
A.1,4
B.1,2
C.0,5
D.1,1
16.多项式2x5y-3x2y2-6xy2-8的次数是m,常数项是n,则mn=-48.
17.已知下列式子:①;②-5.8ab3;③;④a2-ab-2b2;⑤x+;⑥;⑦a.
(1)其中哪些是单项式?分别指出它们的系数和次数;
(2)其中哪些是多项式?分别指出它们的项和次数.
解:(1)①②⑦是单项式,系数分别是-,-5.8,1,次数分别是3,4,1.
(2)④,⑥是多项式,④的项分别是a2,-ab,-2b2,次数为2,⑥的项分别是2m2n,-n,,次数为3.
18.多项式(a-2)m2+(2b+1)mn-m+n-7是关于m,n的多项式,若该多项式不含二次项,求3a+2b的值.
解:由题意,得a-2=0,2b+1=0,
所以a=2,b=-.
所以3a+2b=3×2+2×(-)=5.
19.如图,某长方形广场的四个角都有一块半径相同的四分之一圆形的草地,若圆形的半径为r米,长方形的长为a米,宽为b米.
(1)分别用代数式表示草地和空地的面积;
(2)若长方形的长为300米,宽为200米,圆形的半径为10米,求广场空地的面积(计算结果保留到整数)
解:(1)草地面积为:4×πr2=πr2(米2),
空地面积为:(ab-πr2)米2.
(2)当a=300,b=200,r=10时,
ab-πr2=300×200-100π≈59
686(米2)
答:广场空地的面积约为59
686米2.
综合题
20.有一个多项式a10-a9b+a8b2-a7b3+…,按这样的规律写下去,你知道第7项是什么吗?最后一项呢?这是一个几次几项式?有什么规律?
解:可以观察出,从左到右a的指数逐渐减1,b的指数逐渐加1,
所以第7项是a4b6,最后一项是b10,这是关于a,b的十次十一项式,
它的每一项与字母的次数的关系是:
(-1)n+1a11-nbn-1(n代表第n项).
周周练(3.1~3.3)
(时间:45分钟 满分:100分)
一、选择题(每小题3分,共24分)
1.“比a的3倍大5的数”用代数式表示为(A)
A.3a+5
B.3(a+5)
C.3a-5
D.3(a-5)
2.在下列代数式:ab,a+b,ab2+b+1,π+3,+,x2-x+1中,多项式有(B)
A.2个
B.3个
C.4个
D.5个
3.在y3+1,+1,-x2y,,-8z,0中,整式的个数是(C)
A.6
B.3
C.4
D.5
4.三个连续的奇数,若中间一个为2n+1,则最小的数、最大的数分别是(C)
A.2n-1,2n+1
B.2n+1,2n+3
C.2n-1,2n+3
D.2n-1,3n+1
5.下列说法中正确的是(B)
A.代数式一定是单项式
B.单项式一定是代数式
C.单项式x的次数是0
D.单项式-π2x2y2的次数是6
6.一个运算程序输入x后,得到的结果是4x3-2,则这个运算程序是(C)
A.先乘4,然后立方,再减去2
B.先立方,然后减去2,再乘4
C.先立方,然后乘4,再减去2
D.先减去2,然后立方,再乘4
7.某商品进价为a元,商店将其进价提高30%作为零售价销售,在销售旺季过后,商店又以8折(即售价的80%)的价格开展促销活动,这时一件商品的售价为(D)
A.a元
B.0.8a元
C.0.92a元
D.1.04a元
8.当x=2时,ax+3的值是5;当x=-2时,代数式ax-3的值是(A)
A.-5
B.1
C.-1
D.2
二、填空题(每小题4分,共24分)
9.已知多项式x|m|+(m-2)x-10是二次三项式,m为常数,则m的值为-2.
10.若x+y=4,a,b互为倒数,则(x+y)+5ab的值是7.
11.已知|a+1|+(b-2)2=0,则单项式-xa+2byb-a的次数是4.
12.有a名男生和b名女生在社区做义工,他们为建花坛搬砖.男生每人搬了40块,女生每人搬了30块.这a名男生和b名女生一共搬了(40a+30b)块砖.
13.(包头中考)若2x-3y-1=0,则5-4x+6y的值为3.
14.下列式子按一定规律排列:,,,,…,则第10个式子是.
三、解答题(共52分)
15.(6分)把下列代数式中的单项式放入○中,多项式放入□中:
3,a2b,-m,x+2,x2-2x+1,-,,x3y,-9,,.
16.(8分)赋予下列式子不同的含义:
(1)40a;(2)b-3.
解:(1)汽车的速度为a,飞机的速度是汽车的40倍,则飞机的速度就是40a;底边长为40,底边上的高为a的平行四边形的面积为40a.
(2)爸爸的年龄是b,儿子的年龄比爸爸的年龄的还小3,则儿子的年龄为b-3;某种商品的售价为b,进价比售价的还少3,则进价为b-3.
17.(8分)说出下列多项式的次数和常数项:
(1)-x6+x5-2x2-;
(2)-6x3y2-3x2y+2y-5x-2.
解:(1)次数是6,常数项是-.
(2)次数是5,常数项是-2.
18.(10分)列代数式,如果是单项式,请分别指出它们的系数和次数:
(1)某中学组织七年级学生春游,有m名师生租用45座的大客车若干辆,且刚好坐满,那么租用大客车的辆数是多少?
(2)一个长方体的长和宽都是a,高是h,它的体积是多少?
解:(1),是单项式,系数是,次数是1.
(2)a2h,是单项式,系数是1,次数是3.
19.(10分)某种水果第一天以2元的价格卖出a斤,第二天以1.5元的价格卖出b斤,第三天以1.2元的价格卖出c斤.求:
(1)三天共卖出水果多少斤?
(2)这三天销售这种水果共得多少元?
(3)三天的平均售价是多少?并计算当a=30,b=40,c=45时,平均售价是多少?
解:(1)(a+b+c)斤.
(2)(2a+1.5b+1.2c)元.
(3)三天的平均售价为元.
当a=30,b=40,c=45时,平均售价为元.
20.(10分)按如图所示的程序计算:
(1)若开始输入的n的值为20,求最后输出的结果;
(2)若开始输入的n的值为5,你能得到输出的结果吗?
解:(1)210.
(2)输入5时,第一次运算得到的值为15,小于200,不能输出,从转换器可知,应把15再输入到公式计算得120,还是无法输出,再将120输入公式可得7
260,即最后的输出结果为7
260.
3.4 整式的加减
第1课时 合并同类项
基础题
知识点1 同类项的概念
1.(柳州中考)在下列单项式中,与2xy是同类项的是(C)
A.2x2y2
B.3y
C.xy
D.4x
2.下列各组中的两项,不是同类项的是(A)
A.a2b与-3ab2
B.-x2y与2yx2
C.2πr与π2r
D.35与53
知识点2 合并同类项
3.合并同类项-4a2b+3a2b=(-4+3)a2b=-a2b时,依据的运算律是(C)
A.加法交换律
B.乘法交换律
C.乘法分配律
D.乘法结合律
4.(泸州中考)计算3a2-a2的结果是(C)
A.4a2
B.3a2
C.2a2
D.3
5.若5x2y3+ax2y3=8x2y3,则a=3.
6.合并同类项:
(1)2x-3y+5x-8y-2;
解:原式=7x-11y-2.
(2)m-1-m+1+m;
解:原式=m.
(3)6x-10x2+12x2-5x;
解:原式=2x2+x.
(4)x2y-3xy2+2yx2-y2x.
解:原式=3x2y-4xy2.
中档题
7.如果单项式-xa+1y3与ybx2是同类项,那么a、b的值分别为(C)
A.a=2,b=3
B.a=1,b=2
C.a=1,b=3
D.a=2,b=2
8.如果多项式x2-7ab+b2+kab-1不含ab项,那么k的值为(B)
A.0
B.7
C.1
D.不能确定
9.求多项式3a+abc-c2-3a+c2的值,其中a=-,b=2,c=-3.
解:原式=abc.
当a=-,b=2,c=-3时,
原式=-×2×(-3)
=1.
综合题
10.有这样一道题:“当a=0.35,b=-0.28时,求多项式7a3-6a3b+3a2b+3a3+6a3b-3a2b-10a3的值.”小明说:本题中a=0.35,b=-0.28是多余的条件;小强马上反对说:这不可能,多项式中每一项都含有a和b,不给出a,b的值怎么能求出多项式的值呢?你同意哪名同学的观点?请说明理由.
解:我同意小明的观点.
因为7a3-6a3b+3a2b+3a3+6a3b-3a2b-10a3
=(7+3-10)a3+(-6+6)a3b+(3-3)a2b
=0,
所以a=0.35,b=-0.28是多余的条件,故小明的观点正确.
第2课时 去括号
基础题
知识点1 去括号
1.下列去括号正确的是(B)
A.a+(b-c+d)=a+b+c+d
B.a-(b+c-d)=a-b-c+d
C.a-(b-c-d)=a-b-c+d
D.a+(b-c-d)=a-b+c+d
2.下列运算正确的是(D)
A.-2(3x-1)=-6x-1
B.-2(3x-1)=-6x+1
C.-2(3x-1)=-6x-2
D.-2(3x-1)=-6x+2
知识点2 去括号化简整式
3.化简m-n-(m+n)的结果是(C)
A.0
B.2m
C.-2n
D.2m-2n
4.(1)(3x+6)-(2x-7);
解:原式=3x+6-2x+7
=x+13.
(2)-(2x2-xy)+(x2+xy-6);
解:原式=-2x2+xy+x2+xy-6
=-x2+2xy-6.
(3)(4ab-b2)-2(a2+2ab-b2).
解:原式=4ab-b2-2a2-4ab+2b2
=-2a2+b2.
中档题
5.不改变代数式的值,把5x-x2+xy-y的二次项放在前面带有“+”号的括号里,把一次项放在前面带有“-”号的括号里,正确的是(D)
A.(x2+xy)-(5x-y)
B.(-x2-xy)-(5x-y)
C.(-x2-xy)-(y-5x)
D.(-x2+xy)-(y-5x)
6.根据去括号的法则,在方框中填上“+”号或“-”号,正确的是(D)
①2x□(-y+2x)=4x-y;
②(x2+2y2)□(x2+y2)=y2;
③-(2x+3y)□(x-3y)=-3x;
④a□(m+n-p+d)=a-m-n+p-d.
A.+,+,-,-
B.+,-,+,-
C.+,-,-,+
D.+,-,-,-
7.(1)2a-(3a+4b)+(2a+b);
解:原式=2a-3a-4b+2a+b
=a-3b.
(2)3(a2-ab)-5(ab+2a2-1).
解:原式=3a2-3ab-5ab-10a2+5
=-7a2-8ab+5.
8.已知(a+2)2+4|b-5|=0,求(7a+8b)-(-4a+6b)的值.
解:根据题意,得a+2=0,b-5=0.
解得a=-2,b=5.
原式=7a+8b+4a-6b
=11a+2b.
当a=-2,b=5时,
原式=-22+10
=-12.
第3课时 整式的加减
基础题
知识点1 整式的加减
1.计算(6a2-5a+3)-(5a2+2a-1)的结果是(D)
A.a2-3a+4
B.a2-3a+2
C.a2-7a+2
D.a2-7a+4
2.化简5(2x-3)+4(3-2x)的结果为(A)
A.2x-3
B.2x+9
C.8x-3
D.18x-3
3.用2a+5b减去4a-4b的一半,应当得到(D)
A.4a-b
B.b-a
C.a-9b
D.7b
4.减去-2x等于-3x2+2x+1的多项式是(C)
A.-3x2+4x+1
B.3x2-4x-1
C.-3x2+1
D.3x2-1
5.化简:(x2+y2)-3(x2-2y2)=-2x2+7y2.
6.计算:
(1)(-x2+5x+4)+(5x-4+2x2);
解:原式=-x2+5x+4+5x-4+2x2
=x2+10x.
(2)(3a2-ab+7)-(5ab-4a2+7).
解:原式=3a2-ab+7-5ab+4a2-7
=7a2-6ab.
7.化简求值:(5a+2a2-3-4a3)-(-a+3a3-a2),其中a=-2.
解:原式=-7a3+3a2+6a-3.
当a=-2时,原式=53.
8.给出三个多项式:X=2a2+3ab+b2,Y=3a2+3ab,Z=a2+ab,请你任选两个进行加法或减法运算.
解:答案不唯一.
如:X-Z=(2a2+3ab+b2)-(a2+ab)=a2+2ab+b2.
Y-X=(3a2+3ab)-(2a2+3ab+b2)=a2-b2.
知识点2 整式的加减的应用
9.一个长方形的一边长是2a+3b,另一边长是a+b,则这个长方形的周长是(B)
A.12a+16b
B.6a+8b
C.3a+8b
D.6a+4b
10.一根铁丝的长为5a+4b,剪下一部分围成一个长为a,宽为b的长方形,则这根铁丝还剩下3a+2b.
11.已知某三角形的一条边长为m+n,另一条边长比这条边长大m-3,第三条边长等于2n-m,求这个三角形的周长.
解:(m+n)+(m-3)+(m+n)+(2n-m)
=2m+4n-3.
12.某校有A,B,C三个课外活动小组,A小组有学生(x+2y)名,B小组学生人数是A小组学生人数的3倍,C小组比A小组多3名学生,问A,B,C三个课外活动小组共有多少名学生?
解:(x+2y)+3(x+2y)+(x+2y)+3
=5(x+2y)+3
=5x+10y+3(名).
答:A,B,C三个课外活动小组共有(5x+10y+3)名学生.
中档题
13.若A=5a2-4a+3,B=3a2-4a+2,则A与B的大小关系是(B)
A.A=B
B.A>B
C.A<B
D.以上都可能成立
14.一家商店以每包a元的价格买进30包甲种茶叶,又以每包b元的价格买进60包乙种茶叶.如果以每包元的价格卖出这两种茶叶,那么卖完后,这家商店(D)
A.赚了
B.赔了
C.不赔不赚
D.不能确定赔或赚
15.定义新运算“
”:a
b=则当x=3时,计算2
x-4
x的结果为8.
16.某商场一月份的销售额为a元,二月份比一月份销售额多b元,三月份比二月份减少10%,第一季度的销售额总计为(2.9a+1.9b)元;当a=2万元,b=5
000元时,第一季度的总销售额为67__500元.
17.化简求值:
(1)(ab-3a2)-2b2-5ab-(a2-2ab),其中a=1,b=-2;
解:原式=-4a2-2b2-2ab.
当a=1,b=-2时,原式=-8.
(2)2(3b2-a3b)-3(2b2-a2b-a3b)-4a2b,其中a=-,b=8.
解:原式=a3b-a2b.
当a=-,b=8时,原式=-3.
18.先化简,再求值:
4x2-3(x2+2xy-y+2)+(-x2+6xy-y),其中x=2
015,y=-1.你会有什么发现?
解:原式=4x2-3x2-6xy+3y-6-x2+6xy-y
=2y-6.
当y=-1时,原式=-8.
由此可知,这个多项式的值与字母x的取值无关.
19.已知小明的年龄是m岁,小红的年龄比小明的年龄的2倍少4岁,小华的年龄比小红年龄的还多1岁,求这三名同学的年龄之和是多少.
解:m+(2m-4)+[(2m-4)+1]
=m+2m-4+m-2+1
=4m-5(岁).
答:这三名同学的年龄之和是(4m-5)岁.
综合题
20.老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:
+(-3x2+5x-7)=-2x2+3x-6.
(1)求所捂的多项式;
(2)若x为正整数,任取几个x值并求出所捂多项式的值,你能发现什么规律?
(3)若所捂多项式的值为144,请直接写出x的取值.
解:(1)(-2x2+3x-6)-(-3x2+5x-7)
=-2x2+3x-6+3x2-5x+7
=x2-2x+1,
即所捂的多项式是x2-2x+1.
(2)当x=1时,x2-2x+1=1-2+1=0;
当x=2时,x2-2x+1=4-4+1=1;
当x=3时,x2-2x+1=9-6+1=4;
当x=4时,x2-2x+1=16-8+1=9,
由上可以发现规律是所捂多项式的值是(x-1)2.
(3)x=13.
小专题(四) 整式的化简求值
1.化简下列各式:
(1)2x2-3x+4x2-6x-5;
解:原式=6x2-9x-5.
(2)3xy+4x2y-3xy2-5x2y;
解:原式=3xy-x2y-3xy2.
(3)a2+(5a2-2a)-2(a2-3a);
解:原式=a2+5a2-2a-2a2+6a
=4a2+4a.
(4)3a-[-2b+2(a-3b)-4a].
解:原式=3a-(-2b+2a-6b-4a)
=3a+2b-2a+6b+4a
=5a+8b.
2.先化简,再求值:
(1)(4a+3a2)-3-3a3-(-a+4a3),其中a=-2;
解:原式=-7a3+3a2+5a-3.
当a=-2时,原式=55.
(2)2x-y+(2y2-x2)-(x2+2y2),其中x=-,y=-3;
解:原式=2x-y+2y2-x2-x2-2y2
=-2x2+2x-y.
当x=-,y=-3时,
原式=-2×-1-(-3)=.
(3)4x-[3x-2x-(x-3)],其中x=;
解:原式=4x-3.
当x=时,原式=-1.
(4)3x2y-[2xy2-2(xy-x2y)+xy]+3xy2,其中x=3,y=-.
解:原式=3x2y-2xy2+2xy-3x2y-xy+3xy2
=xy2+xy.
当x=3,y=-时,原式=-.
3.若|x+2|+(y-)2=0,求代数式x3-2x2y+x3+3x2y+5xy2+7-5xy2的值.
解:由题意,得x=-2,y=.
原式=x3+x2y+7
=1.
4.若a2+2b2=5,求多项式(3a2-2ab+b2)-(a2-2ab-3b2)的值.
解:原式=3a2-2ab+b2-a2+2ab+3b2
=2a2+4b2.
当a2+2b2=5时,原式=2(a2+2b2)=10.
5.已知x=-2,y=,求kx-2(x-y2)+(-x+y2)的值.一位同学在做题时把x=-2看成x=2,但结果也正确,已知计算过程无误,求k的值.
解:原式=(k-)x+y2.
由题意知:代数式的值与x无关,
所以k-=0.
解得k=.
6.求m2n+2mn-3nm2-3nm+4m2n的值,其中m是最小的正整数,n是绝对值等于1的数.
解:m2n+2mn-3nm2-3nm+4m2n
=m2n-mn.
由题意知:m=1,n=±1.
当m=1,n=1时,原式=;
当m=1,n=-1时,原式=-.
7.一位同学做一道题:“已知两个多项式A、B,计算2A+B”.他误将“2A+B”看成“A+2B”,求得的结果为9x2-2x+7.已知B=x2+3x-2,请求出正确答案.
解:由题意,得A+2(x2+3x-2)=9x2-2x+7,A=9x2-2x+7-2(x2+3x-2)=9x2-2x+7-2x2-6x+4=7x2-8x+11.
所以正确答案为:2A+B=2(7x2-8x+11)+(x2+3x-2)=14x2-16x+22+x2+3x-2=15x2-13x+20.
8.阅读材料:
如果代数式5a+3b的值为-4,那么代数式2(a+b)+4(2a+b)的值是多少?
我们可以这样来解:
原式=2a+2b+8a+4b=10a+6b.
把式子5a+3b=-4两边同乘以2,
得10a+6b=-8.
仿照上面的解题方法,完成下面的问题:
(1)已知a2+a=0,求a2+a+2
017的值;
(2)已知a-b=-3,求3(a-b)-a+b+5的值;
(3)已知a2+2ab=-2,ab-b2=-4,求2a2+5ab-b2的值.
解:(1)因为a2+a=0,
所以a2+a+2
017=0+2
017=2
017.
(2)因为a-b=-3,
所以3(a-b)-a+b+5
=3×(-3)-(-3)+5
=-1.
(3)因为a2+2ab=-2,ab-b2=-4,
所以2a2+5ab-b2
=2a2+4ab+ab-b2
=2×(-2)+(-4)
=-8.
3.5 探索与表达规律
基础题
知识点1 用代数式表示数的规律
1.观察一串数:0,2,4,6,…,第n个数应为(A)
A.2(n-1)
B.2n-1
C.2(n+1)
D.2n+1
2.在日历中画一个正方形,使它圈起3行3列的9个日期,如果左上角的日期设为n,那么第一行的三个日期依次为n、n+1、n+2;第二行的三个日期依次为n+7、n+8、n+9;第三行的三个日期依次为n+14、n+15、n+16.
3.(广东中考)观察下列一组数:,,,,,…,根据该组数的排列规律,可推出第10个数是.
4.观察:a1=1-,a2=-,a3=-,a4=-,…,则an=-(n=1,2,3,…).
知识点2 用代数式表示图形的规律
5.(重庆中考)下列图形都是由几个黑色和白色的正方形按一定规律组成,图1中有2个黑色正方形,图2中有5个黑色正方形,图3中有8个黑色正方形,图4中有11个黑色正方形,…,依次规律,图10中黑色正方形的个数是(B)
…
图1
图2 图3 图4
A.32
B.29
C.28
D.26
6.(益阳中考)如图是用长度相等的小棒按一定规律摆成的一组图案,第1个图案中有6根小棒,第2个图案中有11根小棒,…,则第n个图案中有(5n+1)根小棒.
7.观察下列图形:
…
它们是按一定规律排列的,依照此规律,第9个图形中共有28个★.
知识点3 用代数式表示表格的规律
8.从2开始,连续的偶数相加,它们和的情况如下表:
加数的个数n
连续偶数的和S
1
2=1×2
2
2+4=6=2×3
3
2+4+6=12=3×4
4
2+4+6+8=20=4×5
5
2+4+6+8+10=30=5×6
…
…
根据表中的规律猜想:用n的代数式表示S的公式为:S=2+4+6+8+…+2n=n(n+1).
中档题
9.如图是将正整数从小到大按1、2、3、4、…、n、…的顺序组成的鱼状图案,则数“n”出现的个数为(A)
A.2n-1
B.2n
C.2n+1
D.2n+2
10.填在下面各正方形中的四个数之间都有相同的规律,根据此规律,m的值是(D)
A.38
B.52
C.66
D.74
11.(宁波中考)下列图案是用长度相同的火柴棒按一定规律拼搭而成,图案①需8根火柴棒,图案②需15根火柴棒,…,按此规律,图案⑦需50根火柴棒.
① ② ③
12.如图是小明用火柴搭的1条、2条、3条“金鱼”…,则搭n条“金鱼”需要火柴(6n+2)根.
13.当n等于1,2,3,…时,由白色小正方形和黑色小正方形组成的图形分别如图所示.则第n个图形中白色小正方形和黑色小正方形的个数总和等于n2+4n.(用n表示,n是正整数)
n=1
n=2
n=3
14.(枣庄中考改编)一列数a1,a2,a3,…满足条件:a1=,an=(n≥2,且n为整数),则a2
017=.
15.如图,按此规律,第6行最后一个数是16,第673行最后一个数是2
017.
1
2
3
4
3
4
5
6
7
4
5
6
7
8
9
10
…
综合题
16.(六盘水中考)毕达哥拉斯学派对“数”与“形”的巧妙结合作了如下研究:
名称及图形几何点数层数
三角形数
正方形数
五边形数
六边形数
第1层几何点数
1
1
1
1
第2层几何点数
2
3
4
5
第3层几何点数
3
5
7
9
…
…
…
…
…
第6层几何点数
▲
▲
▲
▲
…
…
…
…
…
第n层几何点数
▲
▲
▲
▲
写出第6层各个图形的几何点数,并归纳出第n层各个图形的几何点数.
解:因为前三层三角形的几何点数分别是1、2、3,
所以第6层的几何点数是6,第n层的几何点数是n;
因为前三层正方形的几何点数分别是:1=2×1-1、3=2×2-1、5=2×3-1,
所以第6层的几何点数是:2×6-1=11,第n层的几何点数是2n-1;
因为前三层五边形的几何点数分别是:1=3×1-2、4=3×2-2、7=3×3-2,
所以第6层的几何点数是:3×6-2=16,第n层的几何点数是3n-2;
因为前三层六边形的几何点数分别是:1=4×1-3、5=4×2-3、9=4×3-3,
所以第6层的几何点数是:4×6-3=21,第n层的几何点数是4n-3.
小专题(五) 图形的规律探索
——教材P98随堂练习的变式与应用
教材母题(教材P98
随堂练习):下面是用棋子摆成的“小房子”.摆第10个这样的“小房子”需要多少枚棋子?摆第n个这样的“小房子”呢?你是如何得到的?
【思路点拨】 观察图形,把“小房子”分成下边正方形的部分和上边正方形以上的两个部分,分别写出算式,从而得到第n个图形的棋子的枚数,然后把n=10代入进行计算.
【解答】 第1个“小房子”,下边正方形棋子4×2-4=4(枚),上边1枚,共4+1=5(枚);
第2个“小房子”,下边正方形棋子4×3-4=8(枚),上边3枚,共8+3=11(枚);
第3个“小房子”,下边正方形棋子4×4-4=12(枚),上边5枚,共12+5=17(枚);
第4个“小房子”,下边正方形棋子4×5-4=16(枚),上边7枚,共16+7=23(枚);
…
第n个“小房子”,下边正方形棋子4(n+1)-4=4n(枚),上边(2n-1)枚,共4n+2n-1=(6n-1)枚.
当n=10时,6n-1=6×10-1=59(枚).
【方法指导】 解决图形规律探索问题,首先从简单的基本图形入手,随着“序号”或“编号”增加时,后一个图形与前一个图形相比,在数量上的变化情况或图形的变化情况,找出变化规律,从而推出一般性结论.
1.如图是用相同长度的小棒摆成的一组有规律的图案,其中①需要4根小棒,②需要10根小棒,…,按此规律摆下去,则第11个图案所需小棒的根数为(C)
①
②
③ ④
A.70
B.68
C.64
D.58
2.(荆州中考)如图,用黑白两种颜色的纸片,按黑色纸片数逐渐增加1的规律拼成下列图案.若第n个图案中有2
017个白色纸片,则n的值为(B)
第1个 第2个
第3个
A.671
B.672
C.673
D.674
3.(益阳中考)小李用围棋子排成下列一组有规律的图案,其中第1个图案有1枚棋子,第2个图案有3枚棋子,第3个图案有4枚棋子,第4个图案有6枚棋子,…,那么第9个图案的棋子数是13枚.
4.如图是某同学在沙滩上用石子摆成的小房子.观察图形的变化规律,写出第9个小房子用了117块石子.第n个小房子用了(2n-1)+(n+1)2块石子.
5.如图是用棋子摆成的图案:
第1个图
第2个图 第3个图
根据图中棋子的排列规律解决下列问题:
(1)第4个图中有22颗棋子,第5个图中有32颗棋子;
(2)写出你猜想的第n个图中棋子的颗数(用含n的式子表示)是n2+n+2.
周周练(3.4~3.5)
(时间:45分钟 满分:100分)
一、选择题(每小题4分,共32分)
1.下列合并同类项的运算中,结果正确的是(C)
A.2ab+3c=5abc
B.-5ab-(-6ba)=-ab
C.3x2y-3yx2=0
D.m3-2m3=-
2.下列式子正确的是(D)
A.a-(b-c)=a-b-c
B.-(a-b+c)=-a+b+c
C.c+2(a-b)=c+2a-b
D.a-b-c=a-(b+c)
3.某天数学课上,老师讲了整式的加减.放学后,小明回到家拿出课堂笔记,认真地复习老师课堂上讲的内容,他突然发现一道题:
(-x2+3yx-y2)-(-x2+4xy-y2)=-x2________+y2,横线的地方被钢笔水弄污了,那么横线上应是(C)
A.-7xy
B.7xy
C.-xy
D.xy
4.下面计算正确的是(D)
A.3x2-x2=3
B.3a2+2a3=5a5
C.3+x=3x
D.-0.25ab+ba=0
5.化简a-(5a-3b)+(2b-a)的结果是(B)
A.7a-b
B.-5a+5b
C.7a+5b
D.-5a-b
6.已知m-n=100,x+y=-1,则代数式(n+x)-(m-y)的值是(D)
A.99
B.101
C.-99
D.-101
7.当3≤m<5时,化简|2m-10|-|m-3|的结果是(B)
A.13+m
B.13-3m
C.m-7
D.m-13
8.如图,第1个图形中一共有1个小平行四边形,第2个图形中一共有3个小平行四边形,第3个图形中一共有5个小平行四边形,…,则第n个图形中小平行四边形的个数是(D)
A.5n个
B.n2个
C.(n2+n)个
D.(2n-1)个
二、填空题(每小题4分,共24分)
9.若单项式x2ya与-2xby3的和仍为单项式,则其和为-x2y3.
10.填空:3x-(a-b+c)=3x-a+b-c.
11.一个多项式加上(-x2-x-5)得(x2+x-5),则这个多项式为x2+x.
12.一个学生由于粗心,在计算41+N(N为整式)时,误将“+”看成“-”,结果得12,则41+N的值应为70.
13.已知A=x3-2x2+4x+3,B=x2+2x-6,C=x3+2x-3,则A-(B+C)的值是-3x2+12.
14.(新疆中考)如图,下面每个图形中的四个数都是按相同的规律填写的,根据此规律确定x的值为370.
1
1
2
1
2
3
4
10
3
5
6
27
4
7
8
52
…
n
m
20
x
三、解答题(共44分)
15.(12分)计算:
(1)3c3-2c2+8c-13c3+2c-2c2+3;
解:原式=3c3-13c3-2c2-2c2+8c+2c+3
=-10c3-4c2+10c+3.
(2)5x2-2(3y2-5x2)+(-4y2+7xy).
解:原式=5x2-6y2+10x2-4y2+7xy
=(5+10)x2+(-6-4)y2+7xy
=15x2-10y2+7xy.
16.(14分)先化简,再求值:
(1)(3a2-ab+7)-(5ab-4a2+7),其中a=2,b=;
解:原式=3a2-ab+7-5ab+4a2-7
=7a2-6ab.
当a=2,b=时,原式=28-4=24.
(2)3(ab-5b2+2a2)-(7ab+16a2-25b2),其中|a-1|+(b+1)2=0.
解:因为|a-1|+(b+1)2=0,而|a-1|≥0,(b+1)2≥0,
所以a-1=0,b+1=0,即a=1,b=-1.
原式=3ab-15b2+6a2-7ab-16a2+25b2
=-10a2+10b2-4ab.
当a=1,b=-1时,
原式=-10×12+10×(-1)2-4×1×(-1)
=-10+10+4
=4.
17.(8分)小强和小亮同时计算这样一道求值题:“当a=-3时,求整式7a2-[5a-(4a-1)+4a2]-(2a2-a+1)的值.”小亮正确求得结果为7,而小强在计算时,错把a=-3看成了a=3,但计算的结果也正确,你能说明为什么吗?
解:原式=7a2-(5a-4a+1+4a2)-(2a2-a+1)=7a2-4a2-a-1-2a2+a-1=a2-2.
从化简的结果上看,只要a的取值互为相反数,计算的结果总是相等的.
故当a=3或a=-3时,均有a2-2=9-2=7.
所以小强计算的结果正确,但其解题过程错误.
18.(10分)现在房价涨得很厉害,国家为此出台了很多政策,可一些房产商依然不为所动,变着法子涨价.宇宙房产公司对外宣称:今年上半年地价上涨10%,建筑材料上涨10%,广告及人工费用上涨10%,则房价(假定房价由以下三块组成:地价、建筑材料、广告及人工费用)应上涨30%才能保本.你认为“宇宙房产公司”的说法合理吗?如果不合理,那么房价应上涨多少才能保本?
解:表面上看起来,房产商说得好像很有道理:房价既然由三部分构成,每部分上涨10%,当然总价就要上涨30%了.其实这种说法是错误的.
事实上,设房子总价为w元,地价、建筑材料、广告及人工费用分别为a元、b元、c元,则有w=a+b+c.各部分上涨10%,则总价变为a(1+10%)+b(1+10%)+c(1+10%)=(a+b+c)(1+10%)=w(1+10%),即房价上涨10%才是合理的.
章末复习(三) 整式及其加减
基础题
知识点1 代数式
1.以下各式不是代数式的是(C)
A.-
B.-2x+6x2-x
C.a2+b4≠0
D.y
2.(海南中考)某工厂去年的产值是a万元,今年比去年增加10%,今年的产值是(1+10%)a万元.
3.(咸宁中考)体育委员小金带了500元钱去买体育用品,已知一个足球x元,一个篮球y元.则代数式500-3x-2y表示的实际意义是体育委员买了3个足球、2个篮球后剩余的经费.
知识点2 整式
4.下列说法正确的是(D)
A.单项式-的系数是-5,次数是2
B.单项式a的系数为1,次数是0
C.是二次单项式
D.单项式-ab的系数为-,次数是2
5.已知4xy,x2+x-,,y2+y+,2x3-3,0,-+a,m,,,,则其中单项式有4xy,,0,m;多项式有x2+x-,2x3-3,;整式有4xy,x2+x-,,2x3-3,0,m,.
6.(1)多项式2x2y-x2+x2y2-3的最高次项是x2y2,三次项的系数是2,常数项是-3;
(2)多项式-xm-3-2x+1是六次三项式,则m的值是9.
知识点3 整式的加减
7.下列各组中是同类项的是(B)
A.3x2y与2xy2
B.x4y与yx4
C.-2a与0
D.πa2bc3与-3a2cb3
8.去掉下列各式中的括号:
(1)a-(-b+c)=a+b-c;
(2)a+(b-c)=a+b-c;
(3)(a-2b)-(b2-2a2)=a-2b-b2+2a2.
9.计算:
(1)5(2x-3)+4(3-2x);
解:原式=10x-15+12-8x
=2x-3.
(2)3(a2-2ab)-(-ab+b2).
解:原式=3a2-6ab+ab-b2
=3a2-5ab-b2.
知识点4 探索与表达规律
10.按照如图所示的方式摆放餐桌,每个小矩形代表一张餐桌,每个小圆圈代表一个人,按这样规律下去,摆n张餐桌可以坐(4n+2)人.
…
11.如图为手的示意图,在各个手指间标记字母A,B,C,D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始数连续的正整数1,2,3,4,…,当字母B第(2n-1)次出现时(n为正整数),恰好数到的数是6n-4(用含n的代数式表示).
中档题
12.当x=1时,多项式ax2+bx+1的值为3,则多项式-(6a-2b)+(5a-3b)的值等于(D)
A.0
B.1
C.2
D.-2
13.某校组织若干师生到活动基地进行社会实践活动.若学校租用45座的客车x辆,则余下20人无座位;若租用60座的客车则可少租用2辆,且最后一辆还没坐满,则乘坐最后一辆60座客车的人数是(C)
A.200-60x
B.140-15x
C.200-15x
D.140-60x
14.一个十位数字是a,个位数字是b的两位数表示为10a+b,交换这个两位数的十位数字和个位数字,又得一个新的两位数,新数与原数的差是9b-9a.
15.请写出一个符合下列要求的单项式:系数为-5,只含有字母m,n的四次单项式答案不唯一,如:-5m3n,-5m2n2,-5mn3.
16.电影院第一排有m个座位,后面每排比前一排多2个座位,则第n排的座位数为m+2(n-1).
17.(娄底中考)按照如图所示的操作步骤,若输入的值为3,则输出的值为55.
18.计算:
(1)-(-3a2-2ab+9)-(5ab+4a2-6);
解:原式=3a2+2ab-9-5ab-4a2+6
=-a2-3ab-3.
(2)(2x2+x)-[2x+(1-x2)].
解:原式=2x2+x-(2x+1-x2)
=2x2+x-2x-1+x2
=3x2-x-1.
19.如果xay3和-ybx2是同类项,求多项式3(a-b)2-(a-b)+(a-b)2-(a-b)的值.
解:由题意,得a=2,b=3.所以a-b=-1.
所以原式=(a-b)2-(a-b)
=×(-1)2-×(-1)
=.
20.已知3x2y|m|-(m-1)y+5是关于x,y的多项式,且它的最高次项的次数是3,求2m2-3m+1的值.
解:由题意知,2+|m|=3,所以m=-1或m=1.
当m=-1时,原式=2×(-1)2-3×(-1)+1=6.
当m=1时,原式=2×12-3×1+1=0.
综合题
21.一种中性笔售价是5元/支,如果一次买100支以上(不含100支),售价是4元/支.
(1)列代数式表示买n支中性笔所需要的钱数(注意对n的大小要有所考虑);
(2)按照这种售价规定,会不会出现多买比少买反而付钱少的情况?举例说明.
解:(1)当n≤100时,买n支中性笔所需要的钱数为5n;
当n>100时,买n支中性笔所需要的钱数为4n.
(2)按照这种售价规定,会出现多买比少买反而付钱少的情况.如:买101支中性笔需要404元,买100支中性笔需要500元.
3.1 字母表示数
基础题
知识点 用字母表示数
1.教室内有m排座位,每排有n个座位,则这个教室共有座位(A)
A.mn个
B.(m+n)个
C.(m-n)个
D.(2m+2n)个
2.某日的温差为9
℃,最高温度为t
℃,则最低气温可表示为(A)
A.(t-9)℃
B.(9-t)℃
C.(-9-t)℃
D.(t+9)℃
3.(吉林中考)小红要购买珠子串成一条手链.黑色珠子每个a元,白色珠子每个b元,要串成如图所示的手链,小红购买珠子应该花费(A)
A.(3a+4b)元
B.(4a+3b)元
C.4
(a+b)元
D.3
(a+b)元
4.用含字母的式子表示:
(1)x与y两数的差的平方:(x-y)2;
(2)a与b的平方差:a2-b2.
5.小明从每月的零花钱中储存x元钱捐给希望工程,一年下来小明捐款12x元.
6.今年,和你一起升入初中的同学约有15万人,其中男生约有a万人,则女生约有(15-a)万人.
中档题
7.车上有100袋面粉,每袋50千克,取下x袋,车上还有面粉(A)
A.50(100-x)千克
B.(50×100-x)千克
C.100(50-x)千克
D.50x千克
8.张老板以每个a元的单价买进水蜜桃100个,现以每个比单价多20%的价格卖出70个后,再以每个比单价低b元的价格将剩下的30个卖出,则全部水蜜桃共卖(D)
A.[70a+30(a-b)]元
B.[70(1+20%)a+30b]元
C.[100(1+20%)a-30(a-b)]元
D.[70(1+20%)a+30(a-b)]元
9.今年五月份,由于禽流感的影响,某市鸡肉的价格下降了10%,设鸡肉原来的价格为a元/千克,则五月份的价格为0.9a元/千克.
10.10名学生的平均成绩是x,如果另外5名学生每人得84分,那么整个组的平均成绩是分.
11.用字母表示图中阴影部分的面积.
(1)
(2)
解:(1)阴影部分的面积为ab-bx.
(2)阴影部分的面积为R2-πR2.
综合题
12.用黑白两种颜色的正六边形地砖按如图所示的规律,拼成若干个图案.
(1)第4个图案中有白色地砖18块;
(2)第n个图案中有白色地砖(4n+2)块.
3.2 代数式
第1课时 代数式
基础题
知识点1 代数式的概念
1.在a,0,π,,0.2xyz,n-3,-中,代数式的个数是(D)
A.4
B.5
C.6
D.7
知识点2 代数式的意义
2.在下列表述中,不能表示代数式“4a”意义的是(D)
A.4的a倍
B.a的4倍
C.4个a相加
D.4个a相乘
3.实验中学初三年级12个班总共有团员a人,则表示的实际意义是实验中学初三年级平均每班的团员的人数.
4.联系实际背景,说明代数式6a2的意义.
解:答案不唯一,如:6个边长为a的正方形的面积.
知识点3 列代数式
5.x的2倍与y的和的平方用代数式表示为(A)
A.(2x+y)2
B.2x+y2
C.2x2+y2
D.2(x+y)2
6.3月12日某班50名学生到郊外植树,平均每人植树a棵,则该班一共植树50a棵.
7.某种苹果的售价是每千克x元,用面值为100元的人民币购买了5千克,应找回(100-5x)元.
8.小明的存款是a元,小华的存款比小明存款的一半多2元,则小华存款为(a+2)元.
中档题
9.下列语句正确的是(B)
A.1+a不是一个代数式
B.0是代数式
C.S=πr2是一个代数式
D.单独一个字母a不是代数式
10.a表示一个一位数,b表示一个两位数,把a放到b的左边组成一个三位数,则这个三位数可以表示为(C)
A.ab
B.10a+b
C.100a+b
D.a+b
11.一批产品,甲单独做a小时可以完成,乙单独做b小时可以完成,现在已完成了任务的+,则甲、乙的工作情况是甲已工作了2小时,乙已工作了5小时.
12.A、B两地相距150千米,李明驾驶汽车以v千米/小时的速度从A地驶往B地,请你用代数式表示:
(1)李明从A地到B地需要的时间;
(2)如果汽车每小时多行驶10千米,李明从A地到B地需要多长时间?
(3)在(2)的情况下,李明从A地到B地比原计划少用的时间是多少?
解:(1)小时.
(2)小时.
(3)(-)小时.
综合题
13.家家乐超市出售一种商品,其原价为a元,现有三种调价方案:
①先提价20%,再降价20%;②先降价20%,再提价20%;③先提价15%,再降价15%.
(1)问用这三种方案调价结果是否一样?
(2)最后是不是都恢复了原价?
解:(1)①(1+20%)(1-20%)a=0.96a;
②(1-20%)(1+20%)a=0.96a;
③(1+15%)(1-15%)a=0.977
5a.
前两种方案调价结果一样.
(2)这三种方案最后的价格与原价都不一致.
第2课时 代数式值的变化
基础题
知识点1 求代数式的值
1.已知x=1,y=2,则代数式x-y的值为(B)
A.1
B.-1
C.2
D.-3
2.当a=3,b=2时,a2+2ab+b2的值是(D)
A.5
B.13
C.21
D.25
3.当a=2时,代数式3a-1的值是5.
4.当x=-2,y=3时,代数式2x2-3y的值是-1.
知识点2 数值转换机
5.如图是一个数值转换机,输入x,输出3(x-2),下面给出了四种转换步骤,其中不正确的是(C)
A.先减去2,再乘以3
B.先加上-2,再乘以3
C.先乘以3,再减去2
D.先乘以3,再减去6
6.按照如图所示的程序计算当x分别为-3,0时的输出值.
解:程序对应的代数式为2(5x-2).
当x=-3时,2(5x-2)=2×[5×(-3)-2]=2×(-17)=-34;
当x=0时,2(5x-2)=2×(5×0-2)=-4.
知识点3 代数式的值的简单应用
7.人们通常用c表示摄氏温度(℃),f表示华氏温度(?),c与f之间的关系为c=(f-32),当华氏温度为59(?)时,摄氏温度为(B)
A.-15
℃
B.15
℃
C.112.6
℃
D.95.8
℃
8.在三角形的面积公式S=ah中,a表示底边长,h表示底边上的高,若a=3.2
cm,h=5
cm,则S=8cm2.
中档题
9.下列说法正确的有(A)
①代数式的值只与代数式本身有关;②一个含有字母的代数式,只有一个值;③代数式x2+x-1的值为-1.
A.0个
B.1个
C.2个
D.3个
10.根据流程图中的程序,当输入数值x为-2时,输出数值y为(B)
A.4
B.6
C.8
D.10
11.当x=7与x=-7时,代数式3x4-2x2+1的两个值(A)
A.相等
B.互为倒数
C.互为相反数
D.既不相等也不互为相反数
12.已知2x-5y3=3,则9-4(2x-5y3)的值是-3.
13.某商店出售一批水果,最初以每箱a元的价格出售m箱,后来每箱降价为b元,又售出m箱,剩下30箱又以每箱再降价5元出售.
(1)用代数式表示这批水果共售多少元?
(2)如果a=20,b=18,m=60,进这批水果共花去1
500元,那么该商店赚了多少元?
解:(1)[am+bm+30(b-5)]元.
(2)1
170元.
3.3 整式
基础题
知识点1 单项式及其有关概念
1.在,x+1,-2,-,0.72xy,,各式中,单项式的个数是(C)
A.2
B.3
C.4
D.5
2.(台州中考)单项式2a的系数是(A)
A.2
B.2a
C.1
D.a
3.(德宏中考)-4a2b的次数是(A)
A.3
B.2
C.4
D.-4
4.写出下列各单项式的系数和次数:
单项式
y
-x3
ab2c3
-
πr2
系数
1
-1
1
-
π
次数
1
3
6
3
2
知识点2 多项式及其有关概念
5.下列式子:a+2b,,(x2-y2),,0中,多项式的个数是(B)
A.2
B.3
C.4
D.5
6.多项式3x2-2x-1的各项分别是(D)
A.3x2,2x,1
B.3x2,-2x,1
C.-3x2,2x,-1
D.3x2,-2x,-1
7.如果xn+x2-1是五次多项式,那么n的值是(C)
A.3
B.4
C.5
D.6
8.(佛山中考)多项式2a2b-a2b-ab的项数及次数分别是(A)
A.3,3
B.3,2
C.2,3
D.2,2
9.多项式x+3x2-53的次数最高的项是3x2,一次项系数是,常数项是-53,它是二次三项式.
10.一个关于x的多项式,一次项系数是1,二次项系数和常数项都是-,则这个多项式是-x2+x-.
11.填表:
多项式
3a-1
-x+5x2+7
-2x2y+6xy4-3
各项
3a,-1
-x,5x2,7
-2x2y,6xy4,-3
次数
1
2
5
最高次项
3a
5x2
6xy4
几次几项式
一次二项式
二次三项式
五次三项式
知识点3 整式的概念
12.在代数式x2+5,-1,-3x+2,π,,x2+,5x中,整式有(C)
A.3个
B.4个
C.5个
D.6个
中档题
13.下列说法中正确的是(B)
A.是单项式
B.单项式可以看成是只有一项的多项式
C.单项式3(x2+1)的系数是3
D.多项式的常数项
14.如果一个多项式是四次多项式,那么它任何一项的次数(D)
A.都小于4
B.都等于4
C.都不小于4
D.都不大于4
15.(3m-2)x2yn+1是关于x,y的五次单项式,且系数为1,则m,n的值分别是(B)
A.1,4
B.1,2
C.0,5
D.1,1
16.多项式2x5y-3x2y2-6xy2-8的次数是m,常数项是n,则mn=-48.
17.已知下列式子:①;②-5.8ab3;③;④a2-ab-2b2;⑤x+;⑥;⑦a.
(1)其中哪些是单项式?分别指出它们的系数和次数;
(2)其中哪些是多项式?分别指出它们的项和次数.
解:(1)①②⑦是单项式,系数分别是-,-5.8,1,次数分别是3,4,1.
(2)④,⑥是多项式,④的项分别是a2,-ab,-2b2,次数为2,⑥的项分别是2m2n,-n,,次数为3.
18.多项式(a-2)m2+(2b+1)mn-m+n-7是关于m,n的多项式,若该多项式不含二次项,求3a+2b的值.
解:由题意,得a-2=0,2b+1=0,
所以a=2,b=-.
所以3a+2b=3×2+2×(-)=5.
19.如图,某长方形广场的四个角都有一块半径相同的四分之一圆形的草地,若圆形的半径为r米,长方形的长为a米,宽为b米.
(1)分别用代数式表示草地和空地的面积;
(2)若长方形的长为300米,宽为200米,圆形的半径为10米,求广场空地的面积(计算结果保留到整数)
解:(1)草地面积为:4×πr2=πr2(米2),
空地面积为:(ab-πr2)米2.
(2)当a=300,b=200,r=10时,
ab-πr2=300×200-100π≈59
686(米2)
答:广场空地的面积约为59
686米2.
综合题
20.有一个多项式a10-a9b+a8b2-a7b3+…,按这样的规律写下去,你知道第7项是什么吗?最后一项呢?这是一个几次几项式?有什么规律?
解:可以观察出,从左到右a的指数逐渐减1,b的指数逐渐加1,
所以第7项是a4b6,最后一项是b10,这是关于a,b的十次十一项式,
它的每一项与字母的次数的关系是:
(-1)n+1a11-nbn-1(n代表第n项).
周周练(3.1~3.3)
(时间:45分钟 满分:100分)
一、选择题(每小题3分,共24分)
1.“比a的3倍大5的数”用代数式表示为(A)
A.3a+5
B.3(a+5)
C.3a-5
D.3(a-5)
2.在下列代数式:ab,a+b,ab2+b+1,π+3,+,x2-x+1中,多项式有(B)
A.2个
B.3个
C.4个
D.5个
3.在y3+1,+1,-x2y,,-8z,0中,整式的个数是(C)
A.6
B.3
C.4
D.5
4.三个连续的奇数,若中间一个为2n+1,则最小的数、最大的数分别是(C)
A.2n-1,2n+1
B.2n+1,2n+3
C.2n-1,2n+3
D.2n-1,3n+1
5.下列说法中正确的是(B)
A.代数式一定是单项式
B.单项式一定是代数式
C.单项式x的次数是0
D.单项式-π2x2y2的次数是6
6.一个运算程序输入x后,得到的结果是4x3-2,则这个运算程序是(C)
A.先乘4,然后立方,再减去2
B.先立方,然后减去2,再乘4
C.先立方,然后乘4,再减去2
D.先减去2,然后立方,再乘4
7.某商品进价为a元,商店将其进价提高30%作为零售价销售,在销售旺季过后,商店又以8折(即售价的80%)的价格开展促销活动,这时一件商品的售价为(D)
A.a元
B.0.8a元
C.0.92a元
D.1.04a元
8.当x=2时,ax+3的值是5;当x=-2时,代数式ax-3的值是(A)
A.-5
B.1
C.-1
D.2
二、填空题(每小题4分,共24分)
9.已知多项式x|m|+(m-2)x-10是二次三项式,m为常数,则m的值为-2.
10.若x+y=4,a,b互为倒数,则(x+y)+5ab的值是7.
11.已知|a+1|+(b-2)2=0,则单项式-xa+2byb-a的次数是4.
12.有a名男生和b名女生在社区做义工,他们为建花坛搬砖.男生每人搬了40块,女生每人搬了30块.这a名男生和b名女生一共搬了(40a+30b)块砖.
13.(包头中考)若2x-3y-1=0,则5-4x+6y的值为3.
14.下列式子按一定规律排列:,,,,…,则第10个式子是.
三、解答题(共52分)
15.(6分)把下列代数式中的单项式放入○中,多项式放入□中:
3,a2b,-m,x+2,x2-2x+1,-,,x3y,-9,,.
16.(8分)赋予下列式子不同的含义:
(1)40a;(2)b-3.
解:(1)汽车的速度为a,飞机的速度是汽车的40倍,则飞机的速度就是40a;底边长为40,底边上的高为a的平行四边形的面积为40a.
(2)爸爸的年龄是b,儿子的年龄比爸爸的年龄的还小3,则儿子的年龄为b-3;某种商品的售价为b,进价比售价的还少3,则进价为b-3.
17.(8分)说出下列多项式的次数和常数项:
(1)-x6+x5-2x2-;
(2)-6x3y2-3x2y+2y-5x-2.
解:(1)次数是6,常数项是-.
(2)次数是5,常数项是-2.
18.(10分)列代数式,如果是单项式,请分别指出它们的系数和次数:
(1)某中学组织七年级学生春游,有m名师生租用45座的大客车若干辆,且刚好坐满,那么租用大客车的辆数是多少?
(2)一个长方体的长和宽都是a,高是h,它的体积是多少?
解:(1),是单项式,系数是,次数是1.
(2)a2h,是单项式,系数是1,次数是3.
19.(10分)某种水果第一天以2元的价格卖出a斤,第二天以1.5元的价格卖出b斤,第三天以1.2元的价格卖出c斤.求:
(1)三天共卖出水果多少斤?
(2)这三天销售这种水果共得多少元?
(3)三天的平均售价是多少?并计算当a=30,b=40,c=45时,平均售价是多少?
解:(1)(a+b+c)斤.
(2)(2a+1.5b+1.2c)元.
(3)三天的平均售价为元.
当a=30,b=40,c=45时,平均售价为元.
20.(10分)按如图所示的程序计算:
(1)若开始输入的n的值为20,求最后输出的结果;
(2)若开始输入的n的值为5,你能得到输出的结果吗?
解:(1)210.
(2)输入5时,第一次运算得到的值为15,小于200,不能输出,从转换器可知,应把15再输入到公式计算得120,还是无法输出,再将120输入公式可得7
260,即最后的输出结果为7
260.
3.4 整式的加减
第1课时 合并同类项
基础题
知识点1 同类项的概念
1.(柳州中考)在下列单项式中,与2xy是同类项的是(C)
A.2x2y2
B.3y
C.xy
D.4x
2.下列各组中的两项,不是同类项的是(A)
A.a2b与-3ab2
B.-x2y与2yx2
C.2πr与π2r
D.35与53
知识点2 合并同类项
3.合并同类项-4a2b+3a2b=(-4+3)a2b=-a2b时,依据的运算律是(C)
A.加法交换律
B.乘法交换律
C.乘法分配律
D.乘法结合律
4.(泸州中考)计算3a2-a2的结果是(C)
A.4a2
B.3a2
C.2a2
D.3
5.若5x2y3+ax2y3=8x2y3,则a=3.
6.合并同类项:
(1)2x-3y+5x-8y-2;
解:原式=7x-11y-2.
(2)m-1-m+1+m;
解:原式=m.
(3)6x-10x2+12x2-5x;
解:原式=2x2+x.
(4)x2y-3xy2+2yx2-y2x.
解:原式=3x2y-4xy2.
中档题
7.如果单项式-xa+1y3与ybx2是同类项,那么a、b的值分别为(C)
A.a=2,b=3
B.a=1,b=2
C.a=1,b=3
D.a=2,b=2
8.如果多项式x2-7ab+b2+kab-1不含ab项,那么k的值为(B)
A.0
B.7
C.1
D.不能确定
9.求多项式3a+abc-c2-3a+c2的值,其中a=-,b=2,c=-3.
解:原式=abc.
当a=-,b=2,c=-3时,
原式=-×2×(-3)
=1.
综合题
10.有这样一道题:“当a=0.35,b=-0.28时,求多项式7a3-6a3b+3a2b+3a3+6a3b-3a2b-10a3的值.”小明说:本题中a=0.35,b=-0.28是多余的条件;小强马上反对说:这不可能,多项式中每一项都含有a和b,不给出a,b的值怎么能求出多项式的值呢?你同意哪名同学的观点?请说明理由.
解:我同意小明的观点.
因为7a3-6a3b+3a2b+3a3+6a3b-3a2b-10a3
=(7+3-10)a3+(-6+6)a3b+(3-3)a2b
=0,
所以a=0.35,b=-0.28是多余的条件,故小明的观点正确.
第2课时 去括号
基础题
知识点1 去括号
1.下列去括号正确的是(B)
A.a+(b-c+d)=a+b+c+d
B.a-(b+c-d)=a-b-c+d
C.a-(b-c-d)=a-b-c+d
D.a+(b-c-d)=a-b+c+d
2.下列运算正确的是(D)
A.-2(3x-1)=-6x-1
B.-2(3x-1)=-6x+1
C.-2(3x-1)=-6x-2
D.-2(3x-1)=-6x+2
知识点2 去括号化简整式
3.化简m-n-(m+n)的结果是(C)
A.0
B.2m
C.-2n
D.2m-2n
4.(1)(3x+6)-(2x-7);
解:原式=3x+6-2x+7
=x+13.
(2)-(2x2-xy)+(x2+xy-6);
解:原式=-2x2+xy+x2+xy-6
=-x2+2xy-6.
(3)(4ab-b2)-2(a2+2ab-b2).
解:原式=4ab-b2-2a2-4ab+2b2
=-2a2+b2.
中档题
5.不改变代数式的值,把5x-x2+xy-y的二次项放在前面带有“+”号的括号里,把一次项放在前面带有“-”号的括号里,正确的是(D)
A.(x2+xy)-(5x-y)
B.(-x2-xy)-(5x-y)
C.(-x2-xy)-(y-5x)
D.(-x2+xy)-(y-5x)
6.根据去括号的法则,在方框中填上“+”号或“-”号,正确的是(D)
①2x□(-y+2x)=4x-y;
②(x2+2y2)□(x2+y2)=y2;
③-(2x+3y)□(x-3y)=-3x;
④a□(m+n-p+d)=a-m-n+p-d.
A.+,+,-,-
B.+,-,+,-
C.+,-,-,+
D.+,-,-,-
7.(1)2a-(3a+4b)+(2a+b);
解:原式=2a-3a-4b+2a+b
=a-3b.
(2)3(a2-ab)-5(ab+2a2-1).
解:原式=3a2-3ab-5ab-10a2+5
=-7a2-8ab+5.
8.已知(a+2)2+4|b-5|=0,求(7a+8b)-(-4a+6b)的值.
解:根据题意,得a+2=0,b-5=0.
解得a=-2,b=5.
原式=7a+8b+4a-6b
=11a+2b.
当a=-2,b=5时,
原式=-22+10
=-12.
第3课时 整式的加减
基础题
知识点1 整式的加减
1.计算(6a2-5a+3)-(5a2+2a-1)的结果是(D)
A.a2-3a+4
B.a2-3a+2
C.a2-7a+2
D.a2-7a+4
2.化简5(2x-3)+4(3-2x)的结果为(A)
A.2x-3
B.2x+9
C.8x-3
D.18x-3
3.用2a+5b减去4a-4b的一半,应当得到(D)
A.4a-b
B.b-a
C.a-9b
D.7b
4.减去-2x等于-3x2+2x+1的多项式是(C)
A.-3x2+4x+1
B.3x2-4x-1
C.-3x2+1
D.3x2-1
5.化简:(x2+y2)-3(x2-2y2)=-2x2+7y2.
6.计算:
(1)(-x2+5x+4)+(5x-4+2x2);
解:原式=-x2+5x+4+5x-4+2x2
=x2+10x.
(2)(3a2-ab+7)-(5ab-4a2+7).
解:原式=3a2-ab+7-5ab+4a2-7
=7a2-6ab.
7.化简求值:(5a+2a2-3-4a3)-(-a+3a3-a2),其中a=-2.
解:原式=-7a3+3a2+6a-3.
当a=-2时,原式=53.
8.给出三个多项式:X=2a2+3ab+b2,Y=3a2+3ab,Z=a2+ab,请你任选两个进行加法或减法运算.
解:答案不唯一.
如:X-Z=(2a2+3ab+b2)-(a2+ab)=a2+2ab+b2.
Y-X=(3a2+3ab)-(2a2+3ab+b2)=a2-b2.
知识点2 整式的加减的应用
9.一个长方形的一边长是2a+3b,另一边长是a+b,则这个长方形的周长是(B)
A.12a+16b
B.6a+8b
C.3a+8b
D.6a+4b
10.一根铁丝的长为5a+4b,剪下一部分围成一个长为a,宽为b的长方形,则这根铁丝还剩下3a+2b.
11.已知某三角形的一条边长为m+n,另一条边长比这条边长大m-3,第三条边长等于2n-m,求这个三角形的周长.
解:(m+n)+(m-3)+(m+n)+(2n-m)
=2m+4n-3.
12.某校有A,B,C三个课外活动小组,A小组有学生(x+2y)名,B小组学生人数是A小组学生人数的3倍,C小组比A小组多3名学生,问A,B,C三个课外活动小组共有多少名学生?
解:(x+2y)+3(x+2y)+(x+2y)+3
=5(x+2y)+3
=5x+10y+3(名).
答:A,B,C三个课外活动小组共有(5x+10y+3)名学生.
中档题
13.若A=5a2-4a+3,B=3a2-4a+2,则A与B的大小关系是(B)
A.A=B
B.A>B
C.A<B
D.以上都可能成立
14.一家商店以每包a元的价格买进30包甲种茶叶,又以每包b元的价格买进60包乙种茶叶.如果以每包元的价格卖出这两种茶叶,那么卖完后,这家商店(D)
A.赚了
B.赔了
C.不赔不赚
D.不能确定赔或赚
15.定义新运算“
”:a
b=则当x=3时,计算2
x-4
x的结果为8.
16.某商场一月份的销售额为a元,二月份比一月份销售额多b元,三月份比二月份减少10%,第一季度的销售额总计为(2.9a+1.9b)元;当a=2万元,b=5
000元时,第一季度的总销售额为67__500元.
17.化简求值:
(1)(ab-3a2)-2b2-5ab-(a2-2ab),其中a=1,b=-2;
解:原式=-4a2-2b2-2ab.
当a=1,b=-2时,原式=-8.
(2)2(3b2-a3b)-3(2b2-a2b-a3b)-4a2b,其中a=-,b=8.
解:原式=a3b-a2b.
当a=-,b=8时,原式=-3.
18.先化简,再求值:
4x2-3(x2+2xy-y+2)+(-x2+6xy-y),其中x=2
015,y=-1.你会有什么发现?
解:原式=4x2-3x2-6xy+3y-6-x2+6xy-y
=2y-6.
当y=-1时,原式=-8.
由此可知,这个多项式的值与字母x的取值无关.
19.已知小明的年龄是m岁,小红的年龄比小明的年龄的2倍少4岁,小华的年龄比小红年龄的还多1岁,求这三名同学的年龄之和是多少.
解:m+(2m-4)+[(2m-4)+1]
=m+2m-4+m-2+1
=4m-5(岁).
答:这三名同学的年龄之和是(4m-5)岁.
综合题
20.老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:
+(-3x2+5x-7)=-2x2+3x-6.
(1)求所捂的多项式;
(2)若x为正整数,任取几个x值并求出所捂多项式的值,你能发现什么规律?
(3)若所捂多项式的值为144,请直接写出x的取值.
解:(1)(-2x2+3x-6)-(-3x2+5x-7)
=-2x2+3x-6+3x2-5x+7
=x2-2x+1,
即所捂的多项式是x2-2x+1.
(2)当x=1时,x2-2x+1=1-2+1=0;
当x=2时,x2-2x+1=4-4+1=1;
当x=3时,x2-2x+1=9-6+1=4;
当x=4时,x2-2x+1=16-8+1=9,
由上可以发现规律是所捂多项式的值是(x-1)2.
(3)x=13.
小专题(四) 整式的化简求值
1.化简下列各式:
(1)2x2-3x+4x2-6x-5;
解:原式=6x2-9x-5.
(2)3xy+4x2y-3xy2-5x2y;
解:原式=3xy-x2y-3xy2.
(3)a2+(5a2-2a)-2(a2-3a);
解:原式=a2+5a2-2a-2a2+6a
=4a2+4a.
(4)3a-[-2b+2(a-3b)-4a].
解:原式=3a-(-2b+2a-6b-4a)
=3a+2b-2a+6b+4a
=5a+8b.
2.先化简,再求值:
(1)(4a+3a2)-3-3a3-(-a+4a3),其中a=-2;
解:原式=-7a3+3a2+5a-3.
当a=-2时,原式=55.
(2)2x-y+(2y2-x2)-(x2+2y2),其中x=-,y=-3;
解:原式=2x-y+2y2-x2-x2-2y2
=-2x2+2x-y.
当x=-,y=-3时,
原式=-2×-1-(-3)=.
(3)4x-[3x-2x-(x-3)],其中x=;
解:原式=4x-3.
当x=时,原式=-1.
(4)3x2y-[2xy2-2(xy-x2y)+xy]+3xy2,其中x=3,y=-.
解:原式=3x2y-2xy2+2xy-3x2y-xy+3xy2
=xy2+xy.
当x=3,y=-时,原式=-.
3.若|x+2|+(y-)2=0,求代数式x3-2x2y+x3+3x2y+5xy2+7-5xy2的值.
解:由题意,得x=-2,y=.
原式=x3+x2y+7
=1.
4.若a2+2b2=5,求多项式(3a2-2ab+b2)-(a2-2ab-3b2)的值.
解:原式=3a2-2ab+b2-a2+2ab+3b2
=2a2+4b2.
当a2+2b2=5时,原式=2(a2+2b2)=10.
5.已知x=-2,y=,求kx-2(x-y2)+(-x+y2)的值.一位同学在做题时把x=-2看成x=2,但结果也正确,已知计算过程无误,求k的值.
解:原式=(k-)x+y2.
由题意知:代数式的值与x无关,
所以k-=0.
解得k=.
6.求m2n+2mn-3nm2-3nm+4m2n的值,其中m是最小的正整数,n是绝对值等于1的数.
解:m2n+2mn-3nm2-3nm+4m2n
=m2n-mn.
由题意知:m=1,n=±1.
当m=1,n=1时,原式=;
当m=1,n=-1时,原式=-.
7.一位同学做一道题:“已知两个多项式A、B,计算2A+B”.他误将“2A+B”看成“A+2B”,求得的结果为9x2-2x+7.已知B=x2+3x-2,请求出正确答案.
解:由题意,得A+2(x2+3x-2)=9x2-2x+7,A=9x2-2x+7-2(x2+3x-2)=9x2-2x+7-2x2-6x+4=7x2-8x+11.
所以正确答案为:2A+B=2(7x2-8x+11)+(x2+3x-2)=14x2-16x+22+x2+3x-2=15x2-13x+20.
8.阅读材料:
如果代数式5a+3b的值为-4,那么代数式2(a+b)+4(2a+b)的值是多少?
我们可以这样来解:
原式=2a+2b+8a+4b=10a+6b.
把式子5a+3b=-4两边同乘以2,
得10a+6b=-8.
仿照上面的解题方法,完成下面的问题:
(1)已知a2+a=0,求a2+a+2
017的值;
(2)已知a-b=-3,求3(a-b)-a+b+5的值;
(3)已知a2+2ab=-2,ab-b2=-4,求2a2+5ab-b2的值.
解:(1)因为a2+a=0,
所以a2+a+2
017=0+2
017=2
017.
(2)因为a-b=-3,
所以3(a-b)-a+b+5
=3×(-3)-(-3)+5
=-1.
(3)因为a2+2ab=-2,ab-b2=-4,
所以2a2+5ab-b2
=2a2+4ab+ab-b2
=2×(-2)+(-4)
=-8.
3.5 探索与表达规律
基础题
知识点1 用代数式表示数的规律
1.观察一串数:0,2,4,6,…,第n个数应为(A)
A.2(n-1)
B.2n-1
C.2(n+1)
D.2n+1
2.在日历中画一个正方形,使它圈起3行3列的9个日期,如果左上角的日期设为n,那么第一行的三个日期依次为n、n+1、n+2;第二行的三个日期依次为n+7、n+8、n+9;第三行的三个日期依次为n+14、n+15、n+16.
3.(广东中考)观察下列一组数:,,,,,…,根据该组数的排列规律,可推出第10个数是.
4.观察:a1=1-,a2=-,a3=-,a4=-,…,则an=-(n=1,2,3,…).
知识点2 用代数式表示图形的规律
5.(重庆中考)下列图形都是由几个黑色和白色的正方形按一定规律组成,图1中有2个黑色正方形,图2中有5个黑色正方形,图3中有8个黑色正方形,图4中有11个黑色正方形,…,依次规律,图10中黑色正方形的个数是(B)
…
图1
图2 图3 图4
A.32
B.29
C.28
D.26
6.(益阳中考)如图是用长度相等的小棒按一定规律摆成的一组图案,第1个图案中有6根小棒,第2个图案中有11根小棒,…,则第n个图案中有(5n+1)根小棒.
7.观察下列图形:
…
它们是按一定规律排列的,依照此规律,第9个图形中共有28个★.
知识点3 用代数式表示表格的规律
8.从2开始,连续的偶数相加,它们和的情况如下表:
加数的个数n
连续偶数的和S
1
2=1×2
2
2+4=6=2×3
3
2+4+6=12=3×4
4
2+4+6+8=20=4×5
5
2+4+6+8+10=30=5×6
…
…
根据表中的规律猜想:用n的代数式表示S的公式为:S=2+4+6+8+…+2n=n(n+1).
中档题
9.如图是将正整数从小到大按1、2、3、4、…、n、…的顺序组成的鱼状图案,则数“n”出现的个数为(A)
A.2n-1
B.2n
C.2n+1
D.2n+2
10.填在下面各正方形中的四个数之间都有相同的规律,根据此规律,m的值是(D)
A.38
B.52
C.66
D.74
11.(宁波中考)下列图案是用长度相同的火柴棒按一定规律拼搭而成,图案①需8根火柴棒,图案②需15根火柴棒,…,按此规律,图案⑦需50根火柴棒.
① ② ③
12.如图是小明用火柴搭的1条、2条、3条“金鱼”…,则搭n条“金鱼”需要火柴(6n+2)根.
13.当n等于1,2,3,…时,由白色小正方形和黑色小正方形组成的图形分别如图所示.则第n个图形中白色小正方形和黑色小正方形的个数总和等于n2+4n.(用n表示,n是正整数)
n=1
n=2
n=3
14.(枣庄中考改编)一列数a1,a2,a3,…满足条件:a1=,an=(n≥2,且n为整数),则a2
017=.
15.如图,按此规律,第6行最后一个数是16,第673行最后一个数是2
017.
1
2
3
4
3
4
5
6
7
4
5
6
7
8
9
10
…
综合题
16.(六盘水中考)毕达哥拉斯学派对“数”与“形”的巧妙结合作了如下研究:
名称及图形几何点数层数
三角形数
正方形数
五边形数
六边形数
第1层几何点数
1
1
1
1
第2层几何点数
2
3
4
5
第3层几何点数
3
5
7
9
…
…
…
…
…
第6层几何点数
▲
▲
▲
▲
…
…
…
…
…
第n层几何点数
▲
▲
▲
▲
写出第6层各个图形的几何点数,并归纳出第n层各个图形的几何点数.
解:因为前三层三角形的几何点数分别是1、2、3,
所以第6层的几何点数是6,第n层的几何点数是n;
因为前三层正方形的几何点数分别是:1=2×1-1、3=2×2-1、5=2×3-1,
所以第6层的几何点数是:2×6-1=11,第n层的几何点数是2n-1;
因为前三层五边形的几何点数分别是:1=3×1-2、4=3×2-2、7=3×3-2,
所以第6层的几何点数是:3×6-2=16,第n层的几何点数是3n-2;
因为前三层六边形的几何点数分别是:1=4×1-3、5=4×2-3、9=4×3-3,
所以第6层的几何点数是:4×6-3=21,第n层的几何点数是4n-3.
小专题(五) 图形的规律探索
——教材P98随堂练习的变式与应用
教材母题(教材P98
随堂练习):下面是用棋子摆成的“小房子”.摆第10个这样的“小房子”需要多少枚棋子?摆第n个这样的“小房子”呢?你是如何得到的?
【思路点拨】 观察图形,把“小房子”分成下边正方形的部分和上边正方形以上的两个部分,分别写出算式,从而得到第n个图形的棋子的枚数,然后把n=10代入进行计算.
【解答】 第1个“小房子”,下边正方形棋子4×2-4=4(枚),上边1枚,共4+1=5(枚);
第2个“小房子”,下边正方形棋子4×3-4=8(枚),上边3枚,共8+3=11(枚);
第3个“小房子”,下边正方形棋子4×4-4=12(枚),上边5枚,共12+5=17(枚);
第4个“小房子”,下边正方形棋子4×5-4=16(枚),上边7枚,共16+7=23(枚);
…
第n个“小房子”,下边正方形棋子4(n+1)-4=4n(枚),上边(2n-1)枚,共4n+2n-1=(6n-1)枚.
当n=10时,6n-1=6×10-1=59(枚).
【方法指导】 解决图形规律探索问题,首先从简单的基本图形入手,随着“序号”或“编号”增加时,后一个图形与前一个图形相比,在数量上的变化情况或图形的变化情况,找出变化规律,从而推出一般性结论.
1.如图是用相同长度的小棒摆成的一组有规律的图案,其中①需要4根小棒,②需要10根小棒,…,按此规律摆下去,则第11个图案所需小棒的根数为(C)
①
②
③ ④
A.70
B.68
C.64
D.58
2.(荆州中考)如图,用黑白两种颜色的纸片,按黑色纸片数逐渐增加1的规律拼成下列图案.若第n个图案中有2
017个白色纸片,则n的值为(B)
第1个 第2个
第3个
A.671
B.672
C.673
D.674
3.(益阳中考)小李用围棋子排成下列一组有规律的图案,其中第1个图案有1枚棋子,第2个图案有3枚棋子,第3个图案有4枚棋子,第4个图案有6枚棋子,…,那么第9个图案的棋子数是13枚.
4.如图是某同学在沙滩上用石子摆成的小房子.观察图形的变化规律,写出第9个小房子用了117块石子.第n个小房子用了(2n-1)+(n+1)2块石子.
5.如图是用棋子摆成的图案:
第1个图
第2个图 第3个图
根据图中棋子的排列规律解决下列问题:
(1)第4个图中有22颗棋子,第5个图中有32颗棋子;
(2)写出你猜想的第n个图中棋子的颗数(用含n的式子表示)是n2+n+2.
周周练(3.4~3.5)
(时间:45分钟 满分:100分)
一、选择题(每小题4分,共32分)
1.下列合并同类项的运算中,结果正确的是(C)
A.2ab+3c=5abc
B.-5ab-(-6ba)=-ab
C.3x2y-3yx2=0
D.m3-2m3=-
2.下列式子正确的是(D)
A.a-(b-c)=a-b-c
B.-(a-b+c)=-a+b+c
C.c+2(a-b)=c+2a-b
D.a-b-c=a-(b+c)
3.某天数学课上,老师讲了整式的加减.放学后,小明回到家拿出课堂笔记,认真地复习老师课堂上讲的内容,他突然发现一道题:
(-x2+3yx-y2)-(-x2+4xy-y2)=-x2________+y2,横线的地方被钢笔水弄污了,那么横线上应是(C)
A.-7xy
B.7xy
C.-xy
D.xy
4.下面计算正确的是(D)
A.3x2-x2=3
B.3a2+2a3=5a5
C.3+x=3x
D.-0.25ab+ba=0
5.化简a-(5a-3b)+(2b-a)的结果是(B)
A.7a-b
B.-5a+5b
C.7a+5b
D.-5a-b
6.已知m-n=100,x+y=-1,则代数式(n+x)-(m-y)的值是(D)
A.99
B.101
C.-99
D.-101
7.当3≤m<5时,化简|2m-10|-|m-3|的结果是(B)
A.13+m
B.13-3m
C.m-7
D.m-13
8.如图,第1个图形中一共有1个小平行四边形,第2个图形中一共有3个小平行四边形,第3个图形中一共有5个小平行四边形,…,则第n个图形中小平行四边形的个数是(D)
A.5n个
B.n2个
C.(n2+n)个
D.(2n-1)个
二、填空题(每小题4分,共24分)
9.若单项式x2ya与-2xby3的和仍为单项式,则其和为-x2y3.
10.填空:3x-(a-b+c)=3x-a+b-c.
11.一个多项式加上(-x2-x-5)得(x2+x-5),则这个多项式为x2+x.
12.一个学生由于粗心,在计算41+N(N为整式)时,误将“+”看成“-”,结果得12,则41+N的值应为70.
13.已知A=x3-2x2+4x+3,B=x2+2x-6,C=x3+2x-3,则A-(B+C)的值是-3x2+12.
14.(新疆中考)如图,下面每个图形中的四个数都是按相同的规律填写的,根据此规律确定x的值为370.
1
1
2
1
2
3
4
10
3
5
6
27
4
7
8
52
…
n
m
20
x
三、解答题(共44分)
15.(12分)计算:
(1)3c3-2c2+8c-13c3+2c-2c2+3;
解:原式=3c3-13c3-2c2-2c2+8c+2c+3
=-10c3-4c2+10c+3.
(2)5x2-2(3y2-5x2)+(-4y2+7xy).
解:原式=5x2-6y2+10x2-4y2+7xy
=(5+10)x2+(-6-4)y2+7xy
=15x2-10y2+7xy.
16.(14分)先化简,再求值:
(1)(3a2-ab+7)-(5ab-4a2+7),其中a=2,b=;
解:原式=3a2-ab+7-5ab+4a2-7
=7a2-6ab.
当a=2,b=时,原式=28-4=24.
(2)3(ab-5b2+2a2)-(7ab+16a2-25b2),其中|a-1|+(b+1)2=0.
解:因为|a-1|+(b+1)2=0,而|a-1|≥0,(b+1)2≥0,
所以a-1=0,b+1=0,即a=1,b=-1.
原式=3ab-15b2+6a2-7ab-16a2+25b2
=-10a2+10b2-4ab.
当a=1,b=-1时,
原式=-10×12+10×(-1)2-4×1×(-1)
=-10+10+4
=4.
17.(8分)小强和小亮同时计算这样一道求值题:“当a=-3时,求整式7a2-[5a-(4a-1)+4a2]-(2a2-a+1)的值.”小亮正确求得结果为7,而小强在计算时,错把a=-3看成了a=3,但计算的结果也正确,你能说明为什么吗?
解:原式=7a2-(5a-4a+1+4a2)-(2a2-a+1)=7a2-4a2-a-1-2a2+a-1=a2-2.
从化简的结果上看,只要a的取值互为相反数,计算的结果总是相等的.
故当a=3或a=-3时,均有a2-2=9-2=7.
所以小强计算的结果正确,但其解题过程错误.
18.(10分)现在房价涨得很厉害,国家为此出台了很多政策,可一些房产商依然不为所动,变着法子涨价.宇宙房产公司对外宣称:今年上半年地价上涨10%,建筑材料上涨10%,广告及人工费用上涨10%,则房价(假定房价由以下三块组成:地价、建筑材料、广告及人工费用)应上涨30%才能保本.你认为“宇宙房产公司”的说法合理吗?如果不合理,那么房价应上涨多少才能保本?
解:表面上看起来,房产商说得好像很有道理:房价既然由三部分构成,每部分上涨10%,当然总价就要上涨30%了.其实这种说法是错误的.
事实上,设房子总价为w元,地价、建筑材料、广告及人工费用分别为a元、b元、c元,则有w=a+b+c.各部分上涨10%,则总价变为a(1+10%)+b(1+10%)+c(1+10%)=(a+b+c)(1+10%)=w(1+10%),即房价上涨10%才是合理的.
章末复习(三) 整式及其加减
基础题
知识点1 代数式
1.以下各式不是代数式的是(C)
A.-
B.-2x+6x2-x
C.a2+b4≠0
D.y
2.(海南中考)某工厂去年的产值是a万元,今年比去年增加10%,今年的产值是(1+10%)a万元.
3.(咸宁中考)体育委员小金带了500元钱去买体育用品,已知一个足球x元,一个篮球y元.则代数式500-3x-2y表示的实际意义是体育委员买了3个足球、2个篮球后剩余的经费.
知识点2 整式
4.下列说法正确的是(D)
A.单项式-的系数是-5,次数是2
B.单项式a的系数为1,次数是0
C.是二次单项式
D.单项式-ab的系数为-,次数是2
5.已知4xy,x2+x-,,y2+y+,2x3-3,0,-+a,m,,,,则其中单项式有4xy,,0,m;多项式有x2+x-,2x3-3,;整式有4xy,x2+x-,,2x3-3,0,m,.
6.(1)多项式2x2y-x2+x2y2-3的最高次项是x2y2,三次项的系数是2,常数项是-3;
(2)多项式-xm-3-2x+1是六次三项式,则m的值是9.
知识点3 整式的加减
7.下列各组中是同类项的是(B)
A.3x2y与2xy2
B.x4y与yx4
C.-2a与0
D.πa2bc3与-3a2cb3
8.去掉下列各式中的括号:
(1)a-(-b+c)=a+b-c;
(2)a+(b-c)=a+b-c;
(3)(a-2b)-(b2-2a2)=a-2b-b2+2a2.
9.计算:
(1)5(2x-3)+4(3-2x);
解:原式=10x-15+12-8x
=2x-3.
(2)3(a2-2ab)-(-ab+b2).
解:原式=3a2-6ab+ab-b2
=3a2-5ab-b2.
知识点4 探索与表达规律
10.按照如图所示的方式摆放餐桌,每个小矩形代表一张餐桌,每个小圆圈代表一个人,按这样规律下去,摆n张餐桌可以坐(4n+2)人.
…
11.如图为手的示意图,在各个手指间标记字母A,B,C,D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始数连续的正整数1,2,3,4,…,当字母B第(2n-1)次出现时(n为正整数),恰好数到的数是6n-4(用含n的代数式表示).
中档题
12.当x=1时,多项式ax2+bx+1的值为3,则多项式-(6a-2b)+(5a-3b)的值等于(D)
A.0
B.1
C.2
D.-2
13.某校组织若干师生到活动基地进行社会实践活动.若学校租用45座的客车x辆,则余下20人无座位;若租用60座的客车则可少租用2辆,且最后一辆还没坐满,则乘坐最后一辆60座客车的人数是(C)
A.200-60x
B.140-15x
C.200-15x
D.140-60x
14.一个十位数字是a,个位数字是b的两位数表示为10a+b,交换这个两位数的十位数字和个位数字,又得一个新的两位数,新数与原数的差是9b-9a.
15.请写出一个符合下列要求的单项式:系数为-5,只含有字母m,n的四次单项式答案不唯一,如:-5m3n,-5m2n2,-5mn3.
16.电影院第一排有m个座位,后面每排比前一排多2个座位,则第n排的座位数为m+2(n-1).
17.(娄底中考)按照如图所示的操作步骤,若输入的值为3,则输出的值为55.
18.计算:
(1)-(-3a2-2ab+9)-(5ab+4a2-6);
解:原式=3a2+2ab-9-5ab-4a2+6
=-a2-3ab-3.
(2)(2x2+x)-[2x+(1-x2)].
解:原式=2x2+x-(2x+1-x2)
=2x2+x-2x-1+x2
=3x2-x-1.
19.如果xay3和-ybx2是同类项,求多项式3(a-b)2-(a-b)+(a-b)2-(a-b)的值.
解:由题意,得a=2,b=3.所以a-b=-1.
所以原式=(a-b)2-(a-b)
=×(-1)2-×(-1)
=.
20.已知3x2y|m|-(m-1)y+5是关于x,y的多项式,且它的最高次项的次数是3,求2m2-3m+1的值.
解:由题意知,2+|m|=3,所以m=-1或m=1.
当m=-1时,原式=2×(-1)2-3×(-1)+1=6.
当m=1时,原式=2×12-3×1+1=0.
综合题
21.一种中性笔售价是5元/支,如果一次买100支以上(不含100支),售价是4元/支.
(1)列代数式表示买n支中性笔所需要的钱数(注意对n的大小要有所考虑);
(2)按照这种售价规定,会不会出现多买比少买反而付钱少的情况?举例说明.
解:(1)当n≤100时,买n支中性笔所需要的钱数为5n;
当n>100时,买n支中性笔所需要的钱数为4n.
(2)按照这种售价规定,会出现多买比少买反而付钱少的情况.如:买101支中性笔需要404元,买100支中性笔需要500元.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
