数学北师大版七上第一章 丰富的图形练习题(有答案)
文档属性
| 名称 | 数学北师大版七上第一章 丰富的图形练习题(有答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 850.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-12 00:00:00 | ||
图片预览


文档简介
第一章 丰富的图形世界
1.1 生活中的立体图形
第1课时 认识几何体
基础题
知识点1 几何体的认识
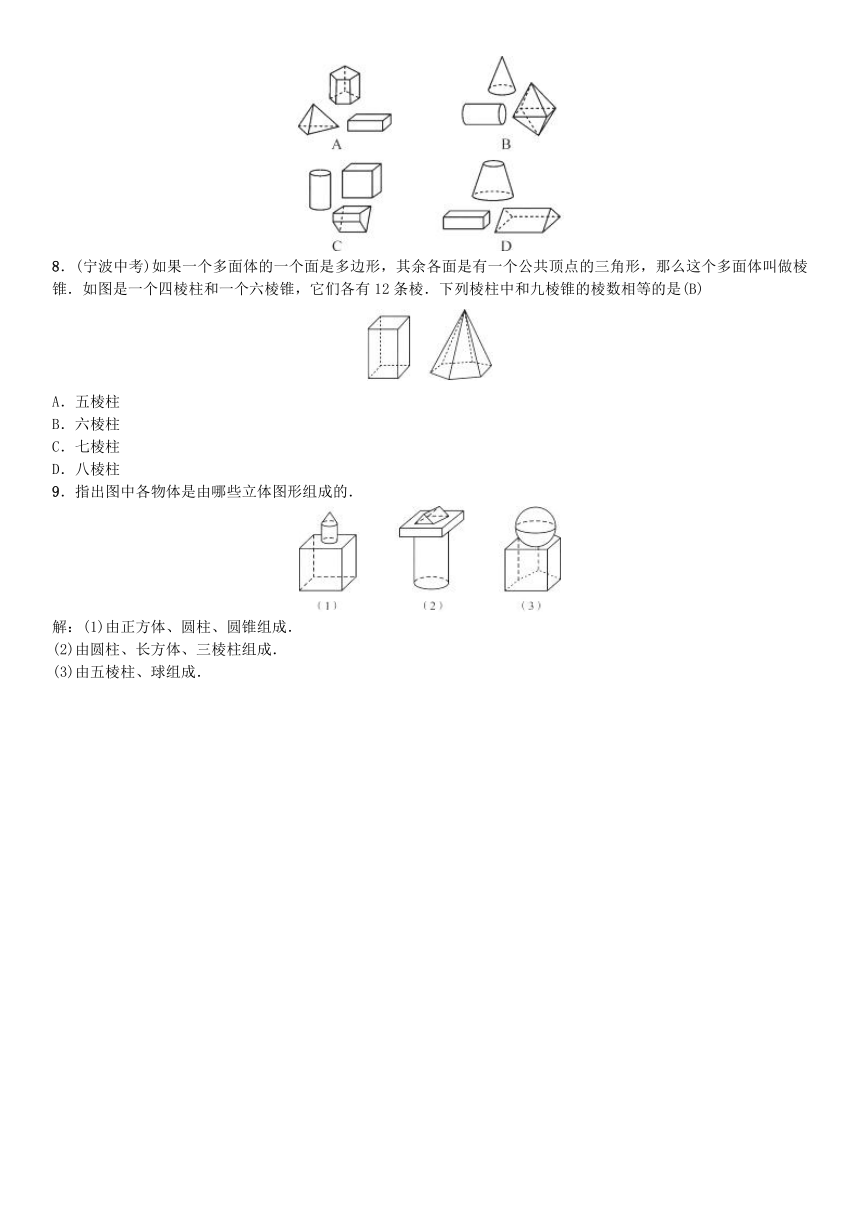
1.(丽水中考)下列图形中,属于立体图形的是(C)
A
B C D
2.下列物体的形状类似于球的是(C)
A.茶杯
B.羽毛球
C.乒乓球
D.白炽灯泡
3.说出与下列物体类似的立体图形名称:
数学课本类似于长方体,西瓜类似于球体,日光灯管类似于圆柱.
知识点2 几何体的分类
4.在如下图所示的图形中,柱体有①②③⑦,锥体有⑤⑥,球体有④.
5.如图所示的是一个棱柱,请问:
(1)这个棱柱由几个面围成?棱的条数为几条?
(2)这个棱柱的底面和侧面各是什么形状?
(3)该棱柱有几个顶点?
解:(1)这个棱柱由5个面围成,棱的条数为9条.
(2)棱柱的底面是三角形,侧面是长方形.
(3)有6个顶点.
中档题
6.下列各几何体中,直棱柱的个数是(C)
A.5
B.4
C.3
D.2
7.如图,下列图形全部属于柱体的是(C)
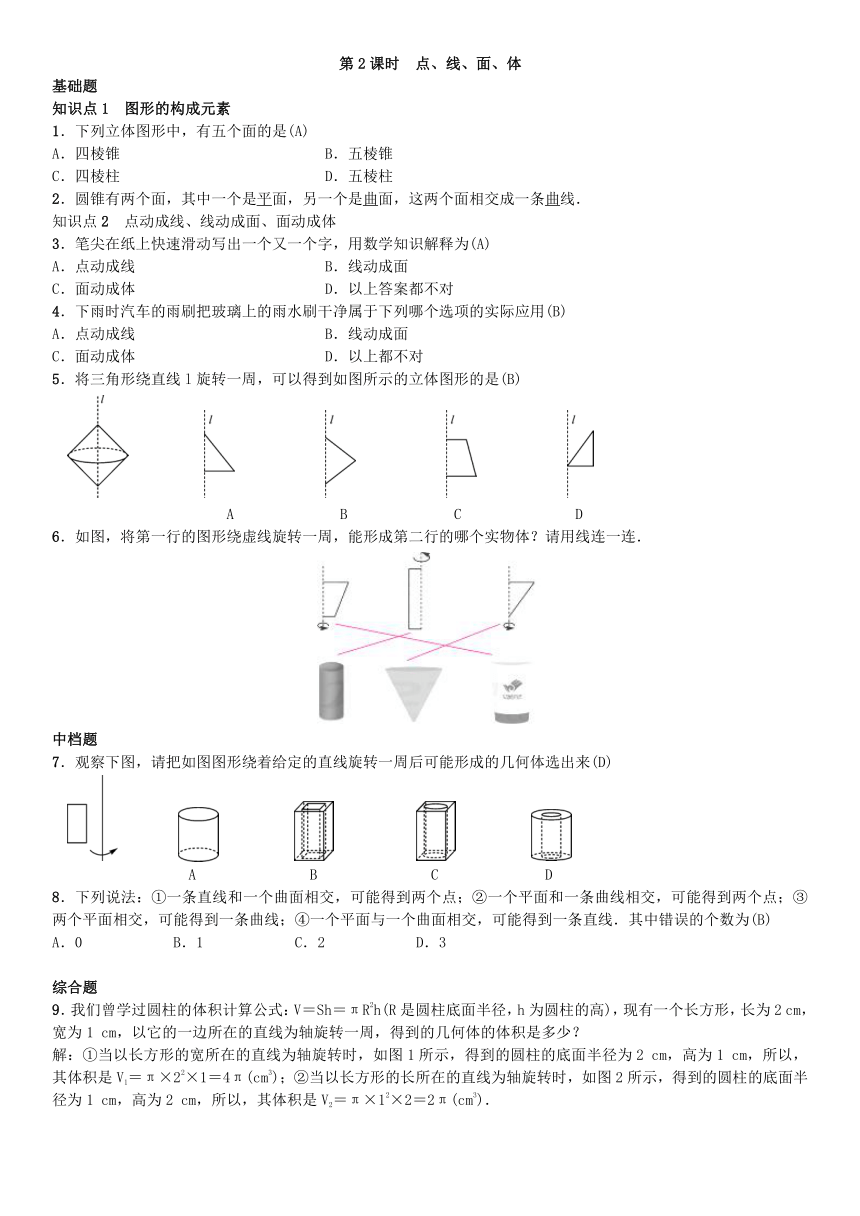
8.(宁波中考)如果一个多面体的一个面是多边形,其余各面是有一个公共顶点的三角形,那么这个多面体叫做棱锥.如图是一个四棱柱和一个六棱锥,它们各有12条棱.下列棱柱中和九棱锥的棱数相等的是(B)
A.五棱柱
B.六棱柱
C.七棱柱
D.八棱柱
9.指出图中各物体是由哪些立体图形组成的.
解:(1)由正方体、圆柱、圆锥组成.
(2)由圆柱、长方体、三棱柱组成.
(3)由五棱柱、球组成.
第2课时 点、线、面、体
基础题
知识点1 图形的构成元素
1.下列立体图形中,有五个面的是(A)
A.四棱锥
B.五棱锥
C.四棱柱
D.五棱柱
2.圆锥有两个面,其中一个是平面,另一个是曲面,这两个面相交成一条曲线.
知识点2 点动成线、线动成面、面动成体
3.笔尖在纸上快速滑动写出一个又一个字,用数学知识解释为(A)
A.点动成线
B.线动成面
C.面动成体
D.以上答案都不对
4.下雨时汽车的雨刷把玻璃上的雨水刷干净属于下列哪个选项的实际应用(B)
A.点动成线
B.线动成面
C.面动成体
D.以上都不对
5.将三角形绕直线l旋转一周,可以得到如图所示的立体图形的是(B)
A B
C
D
6.如图,将第一行的图形绕虚线旋转一周,能形成第二行的哪个实物体?请用线连一连.
中档题
7.观察下图,请把如图图形绕着给定的直线旋转一周后可能形成的几何体选出来(D)
A
B
C D
8.下列说法:①一条直线和一个曲面相交,可能得到两个点;②一个平面和一条曲线相交,可能得到两个点;③两个平面相交,可能得到一条曲线;④一个平面与一个曲面相交,可能得到一条直线.其中错误的个数为(B)
A.0
B.1
C.2
D.3
综合题
9.我们曾学过圆柱的体积计算公式:V=Sh=πR2h(R是圆柱底面半径,h为圆柱的高),现有一个长方形,长为2
cm,宽为1
cm,以它的一边所在的直线为轴旋转一周,得到的几何体的体积是多少?
解:①当以长方形的宽所在的直线为轴旋转时,如图1所示,得到的圆柱的底面半径为2
cm,高为1
cm,所以,其体积是V1=π×22×1=4π(cm3);②当以长方形的长所在的直线为轴旋转时,如图2所示,得到的圆柱的底面半径为1
cm,高为2
cm,所以,其体积是V2=π×12×2=2π(cm3).
所以,得到的几何体的体积是4π
cm3或2π
cm3.
1.2 展开与折叠
第1课时 正方体的展开与折叠
基础题
知识点 正方体的展开与折叠
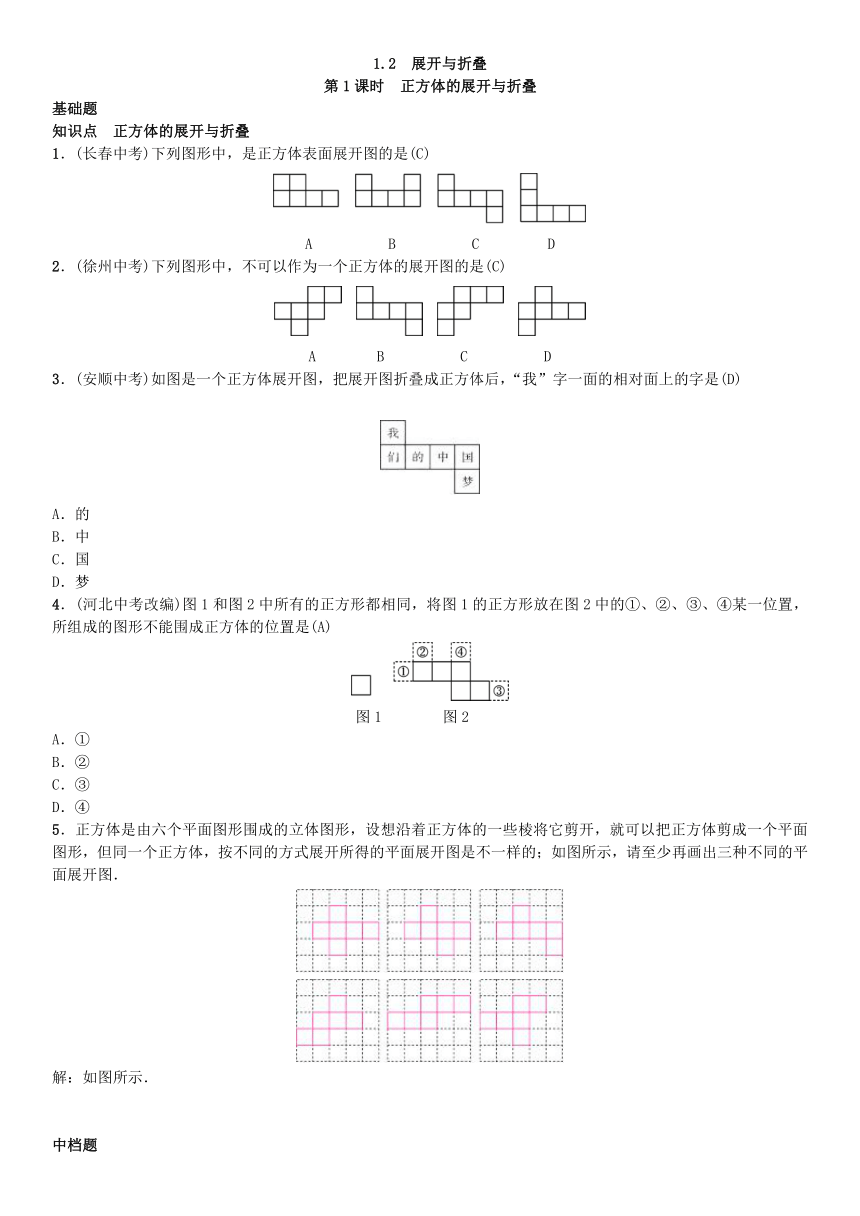
1.(长春中考)下列图形中,是正方体表面展开图的是(C)
A B C
D
2.(徐州中考)下列图形中,不可以作为一个正方体的展开图的是(C)
A B C
D
3.(安顺中考)如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字是(D)
A.的
B.中
C.国
D.梦
4.(河北中考改编)图1和图2中所有的正方形都相同,将图1的正方形放在图2中的①、②、③、④某一位置,所组成的图形不能围成正方体的位置是(A)
图1 图2
A.①
B.②
C.③
D.④
5.正方体是由六个平面图形围成的立体图形,设想沿着正方体的一些棱将它剪开,就可以把正方体剪成一个平面图形,但同一个正方体,按不同的方式展开所得的平面展开图是不一样的;如图所示,请至少再画出三种不同的平面展开图.
解:如图所示.
中档题
6.(恩施中考)正方体的六个面上分别标有1、2、3、4、5、6六个数字,如图是其三种不同的放置方式,与数字“6”相对的面上的数字是(B)
A.1
B.5
C.4
D.3
7.(枣庄中考)有3块积木,每一块的各面都涂上不同的颜色,3块的涂法完全相同,现把它们摆放成不同的位置(如图),请你根据图形判断涂成绿色一面的对面的颜色是(C)
A.白
B.红
C.黄
D.黑
8.如图,在图中增加1个小正方形使所得图形经过折叠能够围成一个正方体,则一共有4种方式.
综合题
9.把立方体的六个面分别涂上六种不同颜色,并画上朵数不等的花,各面上的颜色与花的朵数情况见表:
颜色
红
黄
蓝
白
紫
绿
花的朵数
1
2
3
4
5
6
现将上述大小相同,颜色、花朵分布也完全相同的四个立方体拼成一个水平放置的长方体,如图所示.问长方体的下底面共有多少朵花?
解:因为长方体是由大小相同,颜色、花朵分布也完全相同的四个立方体拼成,所以根据图中红色的面,可以确定出一个小立方体各个面的颜色为:红色面对绿色面,黄色面对紫色面,蓝色面对白色面,所以可知长方体下底面从左到右依次是紫色、黄色、绿色、白色,再由表格中花的朵数可知共有17朵.
第2课时 棱柱、圆柱、圆锥的展开与折叠
基础题
知识点1 棱柱的展开与折叠
1.下列形状的四张纸板,按图中虚线经过折叠可以围成一个三棱柱的是(C)
2.如图是一个长方体包装盒,则它的平面展开图是(A)
3.如图,请你在横线上写出哪种立体图形的表面能展开成下面的图形.
三棱柱 六棱柱 长方体
三棱柱
知识点2 圆柱、圆锥的展开与折叠
4.下列立体图形中,侧面展开图是扇形的是(B)
5.如图,圆柱体的表面展开后得到的平面图形是(B)
6.如图所示的平面图形中,不可能围成圆锥的是(D)
7.用一个宽2
cm,长3
cm的长方形卷成一个圆柱,则此圆柱的侧面积为6__cm2.
中档题
8.按如图的方式把圆锥的侧面展开,得到的图形是(C)
9.如图是一个长方体的展开图,每个面上都标注了字母,如果F面在前面,B面在左面,(字母朝外),那么在上面的字母是C.
综合题
10.小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
①
②
(1)小明总共剪开了8条棱;
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全;
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880
cm,求这个长方体纸盒的体积.
解:(2)如图,四种情况.
(3)因为长方体纸盒的底面是一个正方形,
所以设最短的棱长高为a
cm,则长与宽相等为5a
cm.
因为长方体纸盒所有棱长的和是880
cm,
所以4(a+5a+5a)=880,解得a=20.
所以这个长方体纸盒的体积为:
20×100×100=200
000(立方厘米).
1.3 截一个几何体
基础题
知识点 用平面去截一个几何体
1.如图所示几何体的截面是(B)
A.四边形
B.五边形
C.六边形
D.五棱柱
2.(梅列区校级质检)用一个平面去截一个圆柱体,截面不可能是(B)
3.如图所示的一块长方体木头,沿虚线所示位置截下去所得到的截面图形是(B)
4.用一个平面去截一个几何体,截面的形状是圆形,这个几何体可能是(D)
A.正方体
B.三棱锥
C.五棱柱
D.圆锥体
5.用一个平面去截一个几何体,不能截得三角形截面的几何体是(A)
A.圆柱
B.圆锥
C.三棱柱
D.正方体
6.下列关于截面的说法正确的是(A)
A.截面是一个平面图形
B.截面的形状与所截几何体无关
C.同一个几何体,截面只有一个
D.同一个几何体,截面的形状都相同
7.如图所示的几何体是由一个正方体截去后形成的,这个几何体是由8个面围成的,其中正方形有2个,长方形有4个.
8.将如图所示的几何体的截面用阴影部分表示出来,并分别指出它们的形状.
图1 图2
解:如图1所示,截面是一个三角形;
如图2所示,截面是一个梯形.
9.截几何图形:
(a)用刀将马铃薯、萝卜等切出正方体、长方体、圆柱、圆锥;
(b)用刀截正方体、长方体、圆柱、圆锥.
讨论:(1)(b)的截面各有几种形状?
(2)截面可能是圆的几何体有哪些?
解:(1)正方体和长方体的截面可能是三角形,四边形,五边形,六边形;圆柱的截面可能是圆,长方形;圆锥的截面可能是圆,三角形.
(2)截面可能是圆的几何体有圆柱、圆锥、球.
中档题
10.如图是将正方体切去一个角后的几何体,则该几何体有(A)
A.7个面,14条棱
B.6个面,12条棱
C.7个面,12条棱
D.8个面,13条棱
11.用一平面去截如图所示的5个几何体,能得到长方形截面的几何体的个数是(B)
A.4
B.3
C.2
D.1
12.下列说法正确的是(D)
①正方体的截面可以是等边三角形;②正方体不可能截出七边形;③用一个平面截正方体,当这个平面与四个平面相交时,所得的截面一定是正方形;④正方体的截面中边数最多的是六边形.
A.①②③④
B.①②③
C.①③④
D.①②④
13.一物体的外形为正方体,为探明其内部结构,给其“做CT”,用一组垂直的平面从左向右截这个物体,按顺序得到如下截面,请你猜猜这个正方体的内部构造为正方体中间有一球状(或椭球状等)空洞.
14.用平面截几何体可得到平面图形,在下列表示几何体的字母后填上它可以截出的平面图形的号码.
如A(1、5、6),则B(1、2、3、4);C(5);D(3、5、6).
15.一个圆柱的底面半径是10
cm,高是18
cm,把这个圆柱放在水平桌面上,如图所示.
(1)如果用一个平面沿水平方向去截这个圆柱,所得的截面是什么形状?
(2)如果用一个平面沿竖直方向去截这个圆柱,所得的截面是什么形状?
(3)怎样截时所得的截面是长方形且长方形的面积最大,请你画出这个截面并求其面积.
解:(1)所得的截面是圆.
(2)所得的截面是长方形.
(3)当平面沿竖直方向且经过两个底面的圆心时,截得的长方形面积最大.这时,长方形的一边等于圆柱的高,长方形的另一边等于圆柱的底面直径.则这个长方形的面积为10×2×18=360(cm2).图略.
综合题
16.如图1至图3是将正方体截去一部分后得到的多面体.
(1)根据要求填写表格:
面数(f)
顶点数(v)
棱数(e)
图1
7
9
14
图2
6
8
12
图3
7
10
15
(2)猜想f、v、e三个数量间有何关系;
(3)根据猜想计算,若一个多面体的顶点有2
016个,棱有4
029条,试求出它的面数.
解:(2)f+v-e=2.
(3)因为v=2
016,e=4
029,f+v-e=2,
所以f+2
016-4
029=2.
解得f=2
015,
即它的面数是2
015.
1.4 从三个方向看物体的形状
基础题
知识点1 从三个方向看物体的形状
1.(昆明中考)下面所给几何体从上面看到的是(B)
A
B
C
D
2.(济宁中考)如图,几何体是由3个大小完全一样的正方体组成的,从左边看到的图形是(D)
A
B
C
D
3.(宁波中考)如图所示的几何体从正面看到的图形为(B)
A
B
C
D
4.(安徽中考改编)如图,图中的几何体是圆柱沿竖直方向切掉一半后得到的,若从上面看这个几何体,则所看到的平面图形是(D)
知识点2 由从不同方向看到的物体的形状图确定实物形状
5.如图是一个物体从上面看到的形状图,它所对应的物体是(A)
6.(茂名中考)如图是某几何体从三个不同方向看到的形状,该几何体是(D)
A.球
B.三棱柱
C.圆柱
D.圆锥
知识点3 确定组成几何体的小正方体的个数
7.(大庆中考)由若干边长相等的小正方体构成的几何体从三个不同方向看到的图形如图所示,则构成这个几何体的小正方体有(B)
A.5个
B.6个
C.7个
D.8个
8.用一些大小相同的小正方体组成的几何体从左面看和从上面看到的形状图如图所示,则组成这个几何体的小正方体的块数,最多可能是(C)
A.17块
B.18块
C.19块
D.20块
中档题
9.(陕西中考改编)如图是一个正方体被截去一个直三棱柱得到的几何体,则从左面看这个几何图体,得到的形状图是(A)
10.下列四个几何体:
①正方体 ②球 ③圆锥 ④圆柱
其中从左面与从上面看到的是相同的形状图的几何体共有(B)
A.1个
B.2个
C.3个
D.4个
11.中央电视台有一个非常受欢迎的娱乐节目:墙来了!选手需按墙上的空洞造型摆出相同姿势,才能穿墙而过,否则会被墙推入水池.类似地,有一个几何体恰好无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞,则该几何体为(A)
12.如图是某物体从正面、从左面、从上面三个方向上看所得到的图形,那么物体的形状是圆柱;如果从正面看到的图形的宽为10,长为16,则该物体的表面积为288π.
13.下图是由四个相同的小立方体组成的立体图形从正面和左面看到的形状图,那么原立体图形可能是①②④.(把下图中正确的立体图形的序号都填在横线上)
14.如图是某几何体的三种形状图.
(1)说出这个几何体的名称;
(2)画出它的一种表面展开图.
解:(1)这个几何体是三棱柱.
(2)它的一种表面展开图如图所示.
综合题
15.(教材P18T4变式)由一些大小相同的小正方体组成的简单几何体从正面和上面看到的形状图如图所示.
(1)请你画出这个几何体的一种从左面看到的形状图;
(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值.
解:(1)从左面看到的形状图有以下5种情形(只要画对一种即可):
(2)n=8,9,10,11.
章末复习(一) 丰富的图形世界
基础题
知识点1 生活中的立体图形
1.(东台月考)下列图形属于棱柱的有(B)
A.2个
B.3个
C.4个
D.5个
2.下列说法错误的是(C)
A.长方体、正方体都是棱柱
B.六棱柱有18条棱、6个侧面、12个顶点
C.三棱柱的侧面是三角形
D.圆柱由两个平面和一个曲面围成
3.人在雪地上行走,他的脚印形成一条线,这就是点动成线的原理.
知识点2 图形的展开与折叠
4.(泰州中考)一个几何体的表面展开图如图所示,则这个几何体是(A)
A.四棱锥
B.四棱柱
C.三棱锥
D.三棱柱
5.(河南中考)如图是正方体的一种展开图,其每个面上都标有一个数字,那么在原正方体中,与数字“2”相对的面上的数字是(B)
A.1
B.4
C.5
D.6
6.(通辽中考)妈妈为今年参加中考的女儿小红制作了一个正方体礼品盒(如图),六个面上各有一个字,连起来就是“预祝中考成功”,其中“祝”的对面是“考”,“成”的对面是“功”,则它的平面展开图可能是(D)
知识点3 截一个几何体
7.(玉田中考)如图所示,用一个平面去截一个圆柱,则截得的形状应为(B)
8.用一平面去截下列几何体,其截面可能是长方形的有(C)
A.1个
B.2个
C.3个
D.4个
知识点4 从三个方向看物体的形状
9.(广州中考)从正面看如图所示的几何体得到的平面图形是(A)
10.在下面四个几何体中,从左面看、从上面看分别得到的平面图形是长方形、圆,这个几何体是(A)
11.(山西中考)如图是由几个大小相同的小正方体搭成的几何体从上面看到的图形,小正方形中的数字表示该位置小正方体的个数,则该几何体从左面看到的图形是(A)
A B
C D
中档题
12.(普宁校级月考)下列说法中,正确的个数是(B)
①柱体的两个底面一样大;②圆柱、圆锥的底面都是圆;③棱柱的底面是四边形;④长方体一定是柱体;⑤棱柱的侧面一定是长方形.
A.2
B.3
C.4
D.5
13.(牡丹江中考)如图,由高和直径相同的5个圆柱搭成的几何体,从左边看得到的平面图形是(C)
14.将如图所示放置的一个直角三角形ABC,(∠C=90°),绕斜边AB旋转一周,所得到的几何体从正面看到的图形是下面四个图中的(C)
A
B
C
D
15.(河南模拟)如图是一个正方体被截去一个正三棱锥得到的几何体,从上面看这个几何体,则所看到的平面图形是(B)
16.如图的几何体有9个面,16条棱,9个顶点,它是由简单的几何体四棱锥和四棱柱组成的.
17.围成下面这些立体图形的各个面中,哪些面是平的?哪些面是曲的?
(1) (2)
解:(1)中的5个面都是平的.
(2)中圆锥的侧面是曲的,圆柱的侧面是曲的,圆柱的底面是平的.
综合题
18.(镇江校级期末)如图,图1为一个长方体,AB=AD=16,AE=6,图2为左图的表面展开图,请根据要求回答问题:
(1)面“学”的对面是面“国”;
(2)图1中,M、N为所在棱的中点,试在图2中画出点M、N的位置,并求出图2中△ABN的面积.
解:点M、N如图所示.
因为N是所在棱的中点,
所以点N到AB的距离为AD=×16=8.
所以△ABN的面积为AB×8=×16×8=64.
1.1 生活中的立体图形
第1课时 认识几何体
基础题
知识点1 几何体的认识
1.(丽水中考)下列图形中,属于立体图形的是(C)
A
B C D
2.下列物体的形状类似于球的是(C)
A.茶杯
B.羽毛球
C.乒乓球
D.白炽灯泡
3.说出与下列物体类似的立体图形名称:
数学课本类似于长方体,西瓜类似于球体,日光灯管类似于圆柱.
知识点2 几何体的分类
4.在如下图所示的图形中,柱体有①②③⑦,锥体有⑤⑥,球体有④.
5.如图所示的是一个棱柱,请问:
(1)这个棱柱由几个面围成?棱的条数为几条?
(2)这个棱柱的底面和侧面各是什么形状?
(3)该棱柱有几个顶点?
解:(1)这个棱柱由5个面围成,棱的条数为9条.
(2)棱柱的底面是三角形,侧面是长方形.
(3)有6个顶点.
中档题
6.下列各几何体中,直棱柱的个数是(C)
A.5
B.4
C.3
D.2
7.如图,下列图形全部属于柱体的是(C)
8.(宁波中考)如果一个多面体的一个面是多边形,其余各面是有一个公共顶点的三角形,那么这个多面体叫做棱锥.如图是一个四棱柱和一个六棱锥,它们各有12条棱.下列棱柱中和九棱锥的棱数相等的是(B)
A.五棱柱
B.六棱柱
C.七棱柱
D.八棱柱
9.指出图中各物体是由哪些立体图形组成的.
解:(1)由正方体、圆柱、圆锥组成.
(2)由圆柱、长方体、三棱柱组成.
(3)由五棱柱、球组成.
第2课时 点、线、面、体
基础题
知识点1 图形的构成元素
1.下列立体图形中,有五个面的是(A)
A.四棱锥
B.五棱锥
C.四棱柱
D.五棱柱
2.圆锥有两个面,其中一个是平面,另一个是曲面,这两个面相交成一条曲线.
知识点2 点动成线、线动成面、面动成体
3.笔尖在纸上快速滑动写出一个又一个字,用数学知识解释为(A)
A.点动成线
B.线动成面
C.面动成体
D.以上答案都不对
4.下雨时汽车的雨刷把玻璃上的雨水刷干净属于下列哪个选项的实际应用(B)
A.点动成线
B.线动成面
C.面动成体
D.以上都不对
5.将三角形绕直线l旋转一周,可以得到如图所示的立体图形的是(B)
A B
C
D
6.如图,将第一行的图形绕虚线旋转一周,能形成第二行的哪个实物体?请用线连一连.
中档题
7.观察下图,请把如图图形绕着给定的直线旋转一周后可能形成的几何体选出来(D)
A
B
C D
8.下列说法:①一条直线和一个曲面相交,可能得到两个点;②一个平面和一条曲线相交,可能得到两个点;③两个平面相交,可能得到一条曲线;④一个平面与一个曲面相交,可能得到一条直线.其中错误的个数为(B)
A.0
B.1
C.2
D.3
综合题
9.我们曾学过圆柱的体积计算公式:V=Sh=πR2h(R是圆柱底面半径,h为圆柱的高),现有一个长方形,长为2
cm,宽为1
cm,以它的一边所在的直线为轴旋转一周,得到的几何体的体积是多少?
解:①当以长方形的宽所在的直线为轴旋转时,如图1所示,得到的圆柱的底面半径为2
cm,高为1
cm,所以,其体积是V1=π×22×1=4π(cm3);②当以长方形的长所在的直线为轴旋转时,如图2所示,得到的圆柱的底面半径为1
cm,高为2
cm,所以,其体积是V2=π×12×2=2π(cm3).
所以,得到的几何体的体积是4π
cm3或2π
cm3.
1.2 展开与折叠
第1课时 正方体的展开与折叠
基础题
知识点 正方体的展开与折叠
1.(长春中考)下列图形中,是正方体表面展开图的是(C)
A B C
D
2.(徐州中考)下列图形中,不可以作为一个正方体的展开图的是(C)
A B C
D
3.(安顺中考)如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字是(D)
A.的
B.中
C.国
D.梦
4.(河北中考改编)图1和图2中所有的正方形都相同,将图1的正方形放在图2中的①、②、③、④某一位置,所组成的图形不能围成正方体的位置是(A)
图1 图2
A.①
B.②
C.③
D.④
5.正方体是由六个平面图形围成的立体图形,设想沿着正方体的一些棱将它剪开,就可以把正方体剪成一个平面图形,但同一个正方体,按不同的方式展开所得的平面展开图是不一样的;如图所示,请至少再画出三种不同的平面展开图.
解:如图所示.
中档题
6.(恩施中考)正方体的六个面上分别标有1、2、3、4、5、6六个数字,如图是其三种不同的放置方式,与数字“6”相对的面上的数字是(B)
A.1
B.5
C.4
D.3
7.(枣庄中考)有3块积木,每一块的各面都涂上不同的颜色,3块的涂法完全相同,现把它们摆放成不同的位置(如图),请你根据图形判断涂成绿色一面的对面的颜色是(C)
A.白
B.红
C.黄
D.黑
8.如图,在图中增加1个小正方形使所得图形经过折叠能够围成一个正方体,则一共有4种方式.
综合题
9.把立方体的六个面分别涂上六种不同颜色,并画上朵数不等的花,各面上的颜色与花的朵数情况见表:
颜色
红
黄
蓝
白
紫
绿
花的朵数
1
2
3
4
5
6
现将上述大小相同,颜色、花朵分布也完全相同的四个立方体拼成一个水平放置的长方体,如图所示.问长方体的下底面共有多少朵花?
解:因为长方体是由大小相同,颜色、花朵分布也完全相同的四个立方体拼成,所以根据图中红色的面,可以确定出一个小立方体各个面的颜色为:红色面对绿色面,黄色面对紫色面,蓝色面对白色面,所以可知长方体下底面从左到右依次是紫色、黄色、绿色、白色,再由表格中花的朵数可知共有17朵.
第2课时 棱柱、圆柱、圆锥的展开与折叠
基础题
知识点1 棱柱的展开与折叠
1.下列形状的四张纸板,按图中虚线经过折叠可以围成一个三棱柱的是(C)
2.如图是一个长方体包装盒,则它的平面展开图是(A)
3.如图,请你在横线上写出哪种立体图形的表面能展开成下面的图形.
三棱柱 六棱柱 长方体
三棱柱
知识点2 圆柱、圆锥的展开与折叠
4.下列立体图形中,侧面展开图是扇形的是(B)
5.如图,圆柱体的表面展开后得到的平面图形是(B)
6.如图所示的平面图形中,不可能围成圆锥的是(D)
7.用一个宽2
cm,长3
cm的长方形卷成一个圆柱,则此圆柱的侧面积为6__cm2.
中档题
8.按如图的方式把圆锥的侧面展开,得到的图形是(C)
9.如图是一个长方体的展开图,每个面上都标注了字母,如果F面在前面,B面在左面,(字母朝外),那么在上面的字母是C.
综合题
10.小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
①
②
(1)小明总共剪开了8条棱;
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全;
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880
cm,求这个长方体纸盒的体积.
解:(2)如图,四种情况.
(3)因为长方体纸盒的底面是一个正方形,
所以设最短的棱长高为a
cm,则长与宽相等为5a
cm.
因为长方体纸盒所有棱长的和是880
cm,
所以4(a+5a+5a)=880,解得a=20.
所以这个长方体纸盒的体积为:
20×100×100=200
000(立方厘米).
1.3 截一个几何体
基础题
知识点 用平面去截一个几何体
1.如图所示几何体的截面是(B)
A.四边形
B.五边形
C.六边形
D.五棱柱
2.(梅列区校级质检)用一个平面去截一个圆柱体,截面不可能是(B)
3.如图所示的一块长方体木头,沿虚线所示位置截下去所得到的截面图形是(B)
4.用一个平面去截一个几何体,截面的形状是圆形,这个几何体可能是(D)
A.正方体
B.三棱锥
C.五棱柱
D.圆锥体
5.用一个平面去截一个几何体,不能截得三角形截面的几何体是(A)
A.圆柱
B.圆锥
C.三棱柱
D.正方体
6.下列关于截面的说法正确的是(A)
A.截面是一个平面图形
B.截面的形状与所截几何体无关
C.同一个几何体,截面只有一个
D.同一个几何体,截面的形状都相同
7.如图所示的几何体是由一个正方体截去后形成的,这个几何体是由8个面围成的,其中正方形有2个,长方形有4个.
8.将如图所示的几何体的截面用阴影部分表示出来,并分别指出它们的形状.
图1 图2
解:如图1所示,截面是一个三角形;
如图2所示,截面是一个梯形.
9.截几何图形:
(a)用刀将马铃薯、萝卜等切出正方体、长方体、圆柱、圆锥;
(b)用刀截正方体、长方体、圆柱、圆锥.
讨论:(1)(b)的截面各有几种形状?
(2)截面可能是圆的几何体有哪些?
解:(1)正方体和长方体的截面可能是三角形,四边形,五边形,六边形;圆柱的截面可能是圆,长方形;圆锥的截面可能是圆,三角形.
(2)截面可能是圆的几何体有圆柱、圆锥、球.
中档题
10.如图是将正方体切去一个角后的几何体,则该几何体有(A)
A.7个面,14条棱
B.6个面,12条棱
C.7个面,12条棱
D.8个面,13条棱
11.用一平面去截如图所示的5个几何体,能得到长方形截面的几何体的个数是(B)
A.4
B.3
C.2
D.1
12.下列说法正确的是(D)
①正方体的截面可以是等边三角形;②正方体不可能截出七边形;③用一个平面截正方体,当这个平面与四个平面相交时,所得的截面一定是正方形;④正方体的截面中边数最多的是六边形.
A.①②③④
B.①②③
C.①③④
D.①②④
13.一物体的外形为正方体,为探明其内部结构,给其“做CT”,用一组垂直的平面从左向右截这个物体,按顺序得到如下截面,请你猜猜这个正方体的内部构造为正方体中间有一球状(或椭球状等)空洞.
14.用平面截几何体可得到平面图形,在下列表示几何体的字母后填上它可以截出的平面图形的号码.
如A(1、5、6),则B(1、2、3、4);C(5);D(3、5、6).
15.一个圆柱的底面半径是10
cm,高是18
cm,把这个圆柱放在水平桌面上,如图所示.
(1)如果用一个平面沿水平方向去截这个圆柱,所得的截面是什么形状?
(2)如果用一个平面沿竖直方向去截这个圆柱,所得的截面是什么形状?
(3)怎样截时所得的截面是长方形且长方形的面积最大,请你画出这个截面并求其面积.
解:(1)所得的截面是圆.
(2)所得的截面是长方形.
(3)当平面沿竖直方向且经过两个底面的圆心时,截得的长方形面积最大.这时,长方形的一边等于圆柱的高,长方形的另一边等于圆柱的底面直径.则这个长方形的面积为10×2×18=360(cm2).图略.
综合题
16.如图1至图3是将正方体截去一部分后得到的多面体.
(1)根据要求填写表格:
面数(f)
顶点数(v)
棱数(e)
图1
7
9
14
图2
6
8
12
图3
7
10
15
(2)猜想f、v、e三个数量间有何关系;
(3)根据猜想计算,若一个多面体的顶点有2
016个,棱有4
029条,试求出它的面数.
解:(2)f+v-e=2.
(3)因为v=2
016,e=4
029,f+v-e=2,
所以f+2
016-4
029=2.
解得f=2
015,
即它的面数是2
015.
1.4 从三个方向看物体的形状
基础题
知识点1 从三个方向看物体的形状
1.(昆明中考)下面所给几何体从上面看到的是(B)
A
B
C
D
2.(济宁中考)如图,几何体是由3个大小完全一样的正方体组成的,从左边看到的图形是(D)
A
B
C
D
3.(宁波中考)如图所示的几何体从正面看到的图形为(B)
A
B
C
D
4.(安徽中考改编)如图,图中的几何体是圆柱沿竖直方向切掉一半后得到的,若从上面看这个几何体,则所看到的平面图形是(D)
知识点2 由从不同方向看到的物体的形状图确定实物形状
5.如图是一个物体从上面看到的形状图,它所对应的物体是(A)
6.(茂名中考)如图是某几何体从三个不同方向看到的形状,该几何体是(D)
A.球
B.三棱柱
C.圆柱
D.圆锥
知识点3 确定组成几何体的小正方体的个数
7.(大庆中考)由若干边长相等的小正方体构成的几何体从三个不同方向看到的图形如图所示,则构成这个几何体的小正方体有(B)
A.5个
B.6个
C.7个
D.8个
8.用一些大小相同的小正方体组成的几何体从左面看和从上面看到的形状图如图所示,则组成这个几何体的小正方体的块数,最多可能是(C)
A.17块
B.18块
C.19块
D.20块
中档题
9.(陕西中考改编)如图是一个正方体被截去一个直三棱柱得到的几何体,则从左面看这个几何图体,得到的形状图是(A)
10.下列四个几何体:
①正方体 ②球 ③圆锥 ④圆柱
其中从左面与从上面看到的是相同的形状图的几何体共有(B)
A.1个
B.2个
C.3个
D.4个
11.中央电视台有一个非常受欢迎的娱乐节目:墙来了!选手需按墙上的空洞造型摆出相同姿势,才能穿墙而过,否则会被墙推入水池.类似地,有一个几何体恰好无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞,则该几何体为(A)
12.如图是某物体从正面、从左面、从上面三个方向上看所得到的图形,那么物体的形状是圆柱;如果从正面看到的图形的宽为10,长为16,则该物体的表面积为288π.
13.下图是由四个相同的小立方体组成的立体图形从正面和左面看到的形状图,那么原立体图形可能是①②④.(把下图中正确的立体图形的序号都填在横线上)
14.如图是某几何体的三种形状图.
(1)说出这个几何体的名称;
(2)画出它的一种表面展开图.
解:(1)这个几何体是三棱柱.
(2)它的一种表面展开图如图所示.
综合题
15.(教材P18T4变式)由一些大小相同的小正方体组成的简单几何体从正面和上面看到的形状图如图所示.
(1)请你画出这个几何体的一种从左面看到的形状图;
(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值.
解:(1)从左面看到的形状图有以下5种情形(只要画对一种即可):
(2)n=8,9,10,11.
章末复习(一) 丰富的图形世界
基础题
知识点1 生活中的立体图形
1.(东台月考)下列图形属于棱柱的有(B)
A.2个
B.3个
C.4个
D.5个
2.下列说法错误的是(C)
A.长方体、正方体都是棱柱
B.六棱柱有18条棱、6个侧面、12个顶点
C.三棱柱的侧面是三角形
D.圆柱由两个平面和一个曲面围成
3.人在雪地上行走,他的脚印形成一条线,这就是点动成线的原理.
知识点2 图形的展开与折叠
4.(泰州中考)一个几何体的表面展开图如图所示,则这个几何体是(A)
A.四棱锥
B.四棱柱
C.三棱锥
D.三棱柱
5.(河南中考)如图是正方体的一种展开图,其每个面上都标有一个数字,那么在原正方体中,与数字“2”相对的面上的数字是(B)
A.1
B.4
C.5
D.6
6.(通辽中考)妈妈为今年参加中考的女儿小红制作了一个正方体礼品盒(如图),六个面上各有一个字,连起来就是“预祝中考成功”,其中“祝”的对面是“考”,“成”的对面是“功”,则它的平面展开图可能是(D)
知识点3 截一个几何体
7.(玉田中考)如图所示,用一个平面去截一个圆柱,则截得的形状应为(B)
8.用一平面去截下列几何体,其截面可能是长方形的有(C)
A.1个
B.2个
C.3个
D.4个
知识点4 从三个方向看物体的形状
9.(广州中考)从正面看如图所示的几何体得到的平面图形是(A)
10.在下面四个几何体中,从左面看、从上面看分别得到的平面图形是长方形、圆,这个几何体是(A)
11.(山西中考)如图是由几个大小相同的小正方体搭成的几何体从上面看到的图形,小正方形中的数字表示该位置小正方体的个数,则该几何体从左面看到的图形是(A)
A B
C D
中档题
12.(普宁校级月考)下列说法中,正确的个数是(B)
①柱体的两个底面一样大;②圆柱、圆锥的底面都是圆;③棱柱的底面是四边形;④长方体一定是柱体;⑤棱柱的侧面一定是长方形.
A.2
B.3
C.4
D.5
13.(牡丹江中考)如图,由高和直径相同的5个圆柱搭成的几何体,从左边看得到的平面图形是(C)
14.将如图所示放置的一个直角三角形ABC,(∠C=90°),绕斜边AB旋转一周,所得到的几何体从正面看到的图形是下面四个图中的(C)
A
B
C
D
15.(河南模拟)如图是一个正方体被截去一个正三棱锥得到的几何体,从上面看这个几何体,则所看到的平面图形是(B)
16.如图的几何体有9个面,16条棱,9个顶点,它是由简单的几何体四棱锥和四棱柱组成的.
17.围成下面这些立体图形的各个面中,哪些面是平的?哪些面是曲的?
(1) (2)
解:(1)中的5个面都是平的.
(2)中圆锥的侧面是曲的,圆柱的侧面是曲的,圆柱的底面是平的.
综合题
18.(镇江校级期末)如图,图1为一个长方体,AB=AD=16,AE=6,图2为左图的表面展开图,请根据要求回答问题:
(1)面“学”的对面是面“国”;
(2)图1中,M、N为所在棱的中点,试在图2中画出点M、N的位置,并求出图2中△ABN的面积.
解:点M、N如图所示.
因为N是所在棱的中点,
所以点N到AB的距离为AD=×16=8.
所以△ABN的面积为AB×8=×16×8=64.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
