河北省涞水县2017_2018学年高中数学第一章集合与函数概念1.2.1函数的概念学案(无答案)新人教A版必修1
文档属性
| 名称 | 河北省涞水县2017_2018学年高中数学第一章集合与函数概念1.2.1函数的概念学案(无答案)新人教A版必修1 |

|
|
| 格式 | zip | ||
| 文件大小 | 44.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-14 10:28:24 | ||
图片预览

文档简介
§1.2.1
函数的概念
【学习目标】
通过现实生活中的实例体会函数是描述变量之间的依赖关系得重要模型,理解函数概念;
了解构成函数的三要素:定义域、对应法则、值域,会求一些简单函数的定义域并能说出他们的值域
.
【课前导学】
一、复习回顾
下列函数你认识吗?1)
( http: / / www.21cnjy.com )
2)
( http: / / www.21cnjy.com )
3)
( http: / / www.21cnjy.com )
初中时候函数的定义:_________________________________________
思考:
y=1(x∈R)是函数吗?
二、问题情境
阅读课本23页的问题(1)、(2)、(3),并分别说出对其理解
(1)这一变化过程中,有哪几个变量?
(2)这几个变量的范围分别是多少?
(3)如何用集合的语言来阐述上面3个例子中的共同特点?
【课堂活动】
一、建构数学:
一般地,设A.B是两个_____的数集,如果按某种对应法则f,对于集合A中的______元素x,在集合B中都有_______的元素y和它对应,那么这样的对应叫做从A到B的一个函数(function),通常记作__________,其中,______________定义域(domain),对于A中的每一个x,都有一个输出值y与之对应,我们将所有输出值y组成的集合叫做函数的值域(range).
定义域、值域、对应法则,称为函数的三个要素,缺一不可;
(1)函数作为一种数学模型,主要用于刻画两个变量之间的关系;
(2)函数的本质是一种对应;
(3)y=f(x)不一定是解析式,在不少问题中,对应法则f可能不便使用或不能使用解析式,这时就必须采用其它方式,如数表和图象,在研究函数时,除用符号f(x)表示外,还常用g(x).F(x).G(x)等符号来表示;
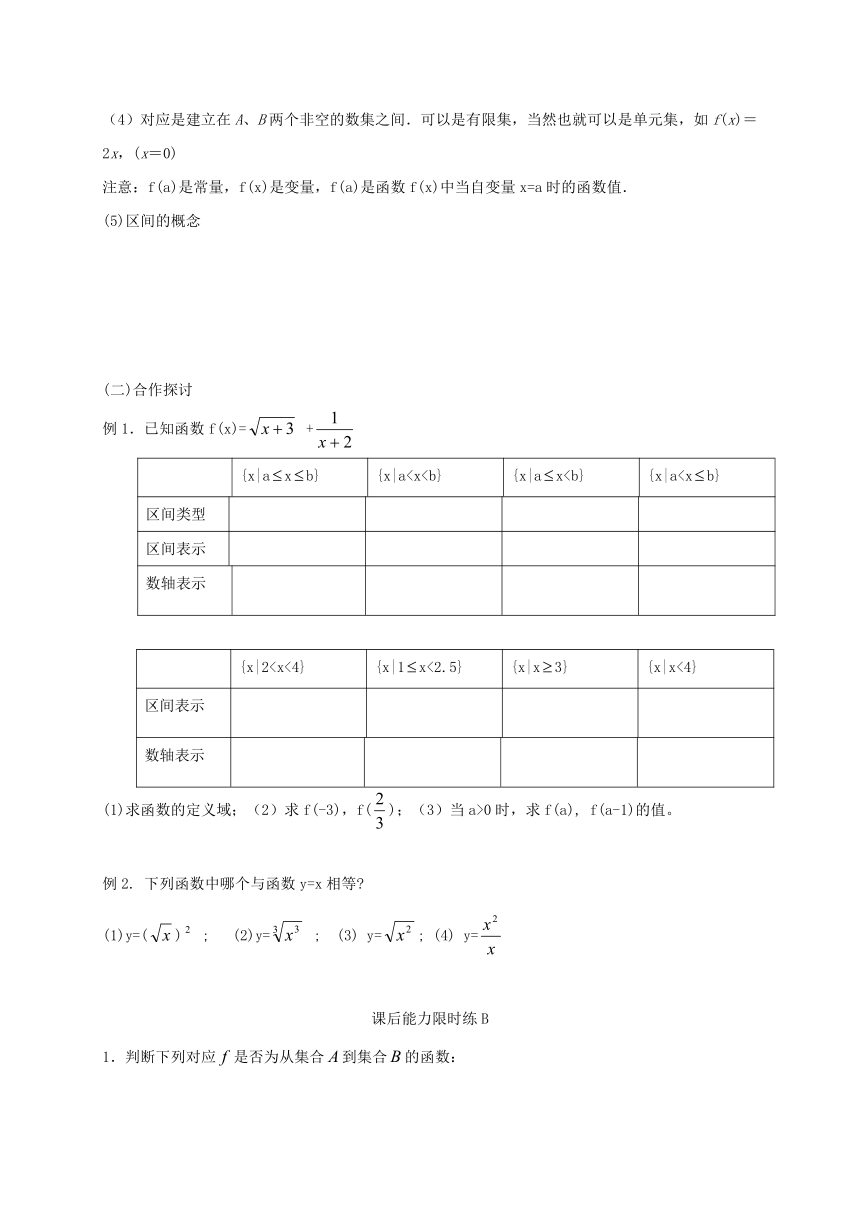
(4)对应是建立在A、B两个非空的数集之间.可以是有限集,当然也就可以是单元集,如f(x)=2x,(x=0)
注意:f(a)是常量,f(x)是变量,f(a)是函数f(x)中当自变量x=a时的函数值.
(5)区间的概念
{x|a
( http: / / www.21cnjy.com )x
( http: / / www.21cnjy.com )b}
{x|a{x|a
( http: / / www.21cnjy.com )x{x|a( http: / / www.21cnjy.com )b}
区间类型
区间表示
数轴表示
{x|2{x|1
( http: / / www.21cnjy.com )x<2.5}
{x|x
( http: / / www.21cnjy.com )3}
{x|x<4}
区间表示
数轴表示
(二)合作探讨
例1.已知函数f(x)=
( http: / / www.21cnjy.com )
+
( http: / / www.21cnjy.com )
(1)求函数的定义域;(2)求f(-3),f(
( http: / / www.21cnjy.com ));(3)当a>0时,求f(a),
f(a-1)的值。
例2.
下列函数中哪个与函数y=x相等
(1)y=(
( http: / / www.21cnjy.com ))
( http: / / www.21cnjy.com )
;
(2)y=
( http: / / www.21cnjy.com )
;
(3)
y=
( http: / / www.21cnjy.com );
(4)
y=
( http: / / www.21cnjy.com )
课后能力限时练B
1.判断下列对应
( http: / / www.21cnjy.com )是否为从集合
( http: / / www.21cnjy.com )到集合
( http: / / www.21cnjy.com )的函数:
①
( http: / / www.21cnjy.com ),
( http: / / www.21cnjy.com ),
( http: / / www.21cnjy.com );
②
( http: / / www.21cnjy.com ),
( http: / / www.21cnjy.com );
③
( http: / / www.21cnjy.com ),
( http: / / www.21cnjy.com );④
( http: / / www.21cnjy.com ),当
( http: / / www.21cnjy.com )为奇数时,
( http: / / www.21cnjy.com );当
( http: / / www.21cnjy.com )为偶数时,
( http: / / www.21cnjy.com )。其中是从集合
( http: / / www.21cnjy.com )到集合
( http: / / www.21cnjy.com )的函数对应的序号为
。
已知集合
( http: / / www.21cnjy.com ),对应法则
( http: / / www.21cnjy.com ),若
( http: / / www.21cnjy.com )为输入值,且
( http: / / www.21cnjy.com ),相应的输出值为
( http: / / www.21cnjy.com ),则
( http: / / www.21cnjy.com )
,
( http: / / www.21cnjy.com )
,0
( http: / / www.21cnjy.com )
,
( http: / / www.21cnjy.com ),
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )。
下列各组式子为同一函数是
(1)
( http: / / www.21cnjy.com ),
( http: / / www.21cnjy.com );(2)
( http: / / www.21cnjy.com ),
( http: / / www.21cnjy.com );
(3)
( http: / / www.21cnjy.com );(4)
( http: / / www.21cnjy.com ),
( http: / / www.21cnjy.com )。
4.若
( http: / / www.21cnjy.com ),则
( http: / / www.21cnjy.com )
。
5.已知函数
( http: / / www.21cnjy.com ),求
( http: / / www.21cnjy.com ).
6.已知
( http: / / www.21cnjy.com ).
(1)求f(2),
g(2)的值;(2)求
( http: / / www.21cnjy.com )的值;(3)求
( http: / / www.21cnjy.com )的解析式。
(三)个人收获与问题
知识:
方法:
函数的概念
【学习目标】
通过现实生活中的实例体会函数是描述变量之间的依赖关系得重要模型,理解函数概念;
了解构成函数的三要素:定义域、对应法则、值域,会求一些简单函数的定义域并能说出他们的值域
.
【课前导学】
一、复习回顾
下列函数你认识吗?1)
( http: / / www.21cnjy.com )
2)
( http: / / www.21cnjy.com )
3)
( http: / / www.21cnjy.com )
初中时候函数的定义:_________________________________________
思考:
y=1(x∈R)是函数吗?
二、问题情境
阅读课本23页的问题(1)、(2)、(3),并分别说出对其理解
(1)这一变化过程中,有哪几个变量?
(2)这几个变量的范围分别是多少?
(3)如何用集合的语言来阐述上面3个例子中的共同特点?
【课堂活动】
一、建构数学:
一般地,设A.B是两个_____的数集,如果按某种对应法则f,对于集合A中的______元素x,在集合B中都有_______的元素y和它对应,那么这样的对应叫做从A到B的一个函数(function),通常记作__________,其中,______________定义域(domain),对于A中的每一个x,都有一个输出值y与之对应,我们将所有输出值y组成的集合叫做函数的值域(range).
定义域、值域、对应法则,称为函数的三个要素,缺一不可;
(1)函数作为一种数学模型,主要用于刻画两个变量之间的关系;
(2)函数的本质是一种对应;
(3)y=f(x)不一定是解析式,在不少问题中,对应法则f可能不便使用或不能使用解析式,这时就必须采用其它方式,如数表和图象,在研究函数时,除用符号f(x)表示外,还常用g(x).F(x).G(x)等符号来表示;
(4)对应是建立在A、B两个非空的数集之间.可以是有限集,当然也就可以是单元集,如f(x)=2x,(x=0)
注意:f(a)是常量,f(x)是变量,f(a)是函数f(x)中当自变量x=a时的函数值.
(5)区间的概念
{x|a
( http: / / www.21cnjy.com )x
( http: / / www.21cnjy.com )b}
{x|a
( http: / / www.21cnjy.com )x
区间类型
区间表示
数轴表示
{x|2
( http: / / www.21cnjy.com )x<2.5}
{x|x
( http: / / www.21cnjy.com )3}
{x|x<4}
区间表示
数轴表示
(二)合作探讨
例1.已知函数f(x)=
( http: / / www.21cnjy.com )
+
( http: / / www.21cnjy.com )
(1)求函数的定义域;(2)求f(-3),f(
( http: / / www.21cnjy.com ));(3)当a>0时,求f(a),
f(a-1)的值。
例2.
下列函数中哪个与函数y=x相等
(1)y=(
( http: / / www.21cnjy.com ))
( http: / / www.21cnjy.com )
;
(2)y=
( http: / / www.21cnjy.com )
;
(3)
y=
( http: / / www.21cnjy.com );
(4)
y=
( http: / / www.21cnjy.com )
课后能力限时练B
1.判断下列对应
( http: / / www.21cnjy.com )是否为从集合
( http: / / www.21cnjy.com )到集合
( http: / / www.21cnjy.com )的函数:
①
( http: / / www.21cnjy.com ),
( http: / / www.21cnjy.com ),
( http: / / www.21cnjy.com );
②
( http: / / www.21cnjy.com ),
( http: / / www.21cnjy.com );
③
( http: / / www.21cnjy.com ),
( http: / / www.21cnjy.com );④
( http: / / www.21cnjy.com ),当
( http: / / www.21cnjy.com )为奇数时,
( http: / / www.21cnjy.com );当
( http: / / www.21cnjy.com )为偶数时,
( http: / / www.21cnjy.com )。其中是从集合
( http: / / www.21cnjy.com )到集合
( http: / / www.21cnjy.com )的函数对应的序号为
。
已知集合
( http: / / www.21cnjy.com ),对应法则
( http: / / www.21cnjy.com ),若
( http: / / www.21cnjy.com )为输入值,且
( http: / / www.21cnjy.com ),相应的输出值为
( http: / / www.21cnjy.com ),则
( http: / / www.21cnjy.com )
,
( http: / / www.21cnjy.com )
,0
( http: / / www.21cnjy.com )
,
( http: / / www.21cnjy.com ),
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )。
下列各组式子为同一函数是
(1)
( http: / / www.21cnjy.com ),
( http: / / www.21cnjy.com );(2)
( http: / / www.21cnjy.com ),
( http: / / www.21cnjy.com );
(3)
( http: / / www.21cnjy.com );(4)
( http: / / www.21cnjy.com ),
( http: / / www.21cnjy.com )。
4.若
( http: / / www.21cnjy.com ),则
( http: / / www.21cnjy.com )
。
5.已知函数
( http: / / www.21cnjy.com ),求
( http: / / www.21cnjy.com ).
6.已知
( http: / / www.21cnjy.com ).
(1)求f(2),
g(2)的值;(2)求
( http: / / www.21cnjy.com )的值;(3)求
( http: / / www.21cnjy.com )的解析式。
(三)个人收获与问题
知识:
方法:
