12.2三角形全等的判定同步练习(解析版)
文档属性
| 名称 | 12.2三角形全等的判定同步练习(解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 450.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-18 08:23:20 | ||
图片预览

文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
新人教版八年级数学上册同步练习
12.2三角形全等的判定
一、单选题
1、如图,在平行四边形ABCD中,连接对角线AC、BD,图中的全等三角形的对数( )
A、1对 B、2对 C、3对 D、4对
2、如图,用直尺和圆规画∠AOB的平分线OE,其理论依据是( )
A、SAS B、ASA C、AAS D、SSS
3、如图,正方形ABCD中,E为CD边上一点,F为BC延长线上一点,CE=CF.若∠BEC=80°,则∠EFD的度数为( )【来源:21cnj*y.co*m】
A、20° B、25° C、35° D、40°
4、如图,在△ABC与△DEF中,B、F、C、E在一条直线上,若BF=CE,AC=FD,则下列补充的条件能说明△ABC≌△DEF的有( ) ①∠E=∠B; ②AC∥DF; ③∠A=∠D.
A、1个 B、2个 C、3个 D、0个
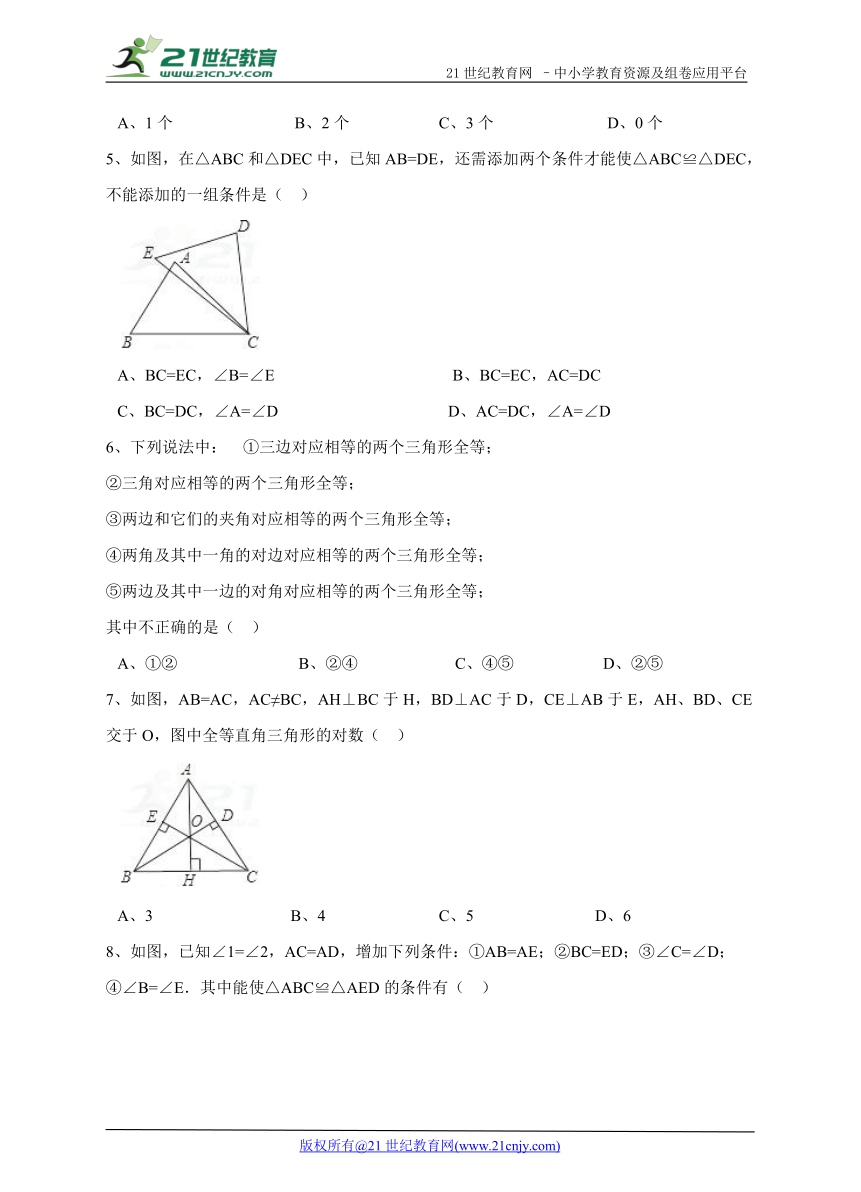
5、如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A、BC=EC,∠B=∠E B、BC=EC,AC=DC
C、BC=DC,∠A=∠D D、AC=DC,∠A=∠D
6、下列说法中: ①三边对应相等的两个三角形全等;
②三角对应相等的两个三角形全等;
③两边和它们的夹角对应相等的两个三角形全等;
④两角及其中一角的对边对应相等的两个三角形全等;
⑤两边及其中一边的对角对应相等的两个三角形全等;
其中不正确的是( )
A、①② B、②④ C、④⑤ D、②⑤
7、如图,AB=AC,AC≠BC,AH⊥BC于H,BD⊥AC于D,CE⊥AB于E,AH、BD、CE交于O,图中全等直角三角形的对数( )
A、3 B、4 C、5 D、6
8、如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的条件有( )21教育名师原创作品
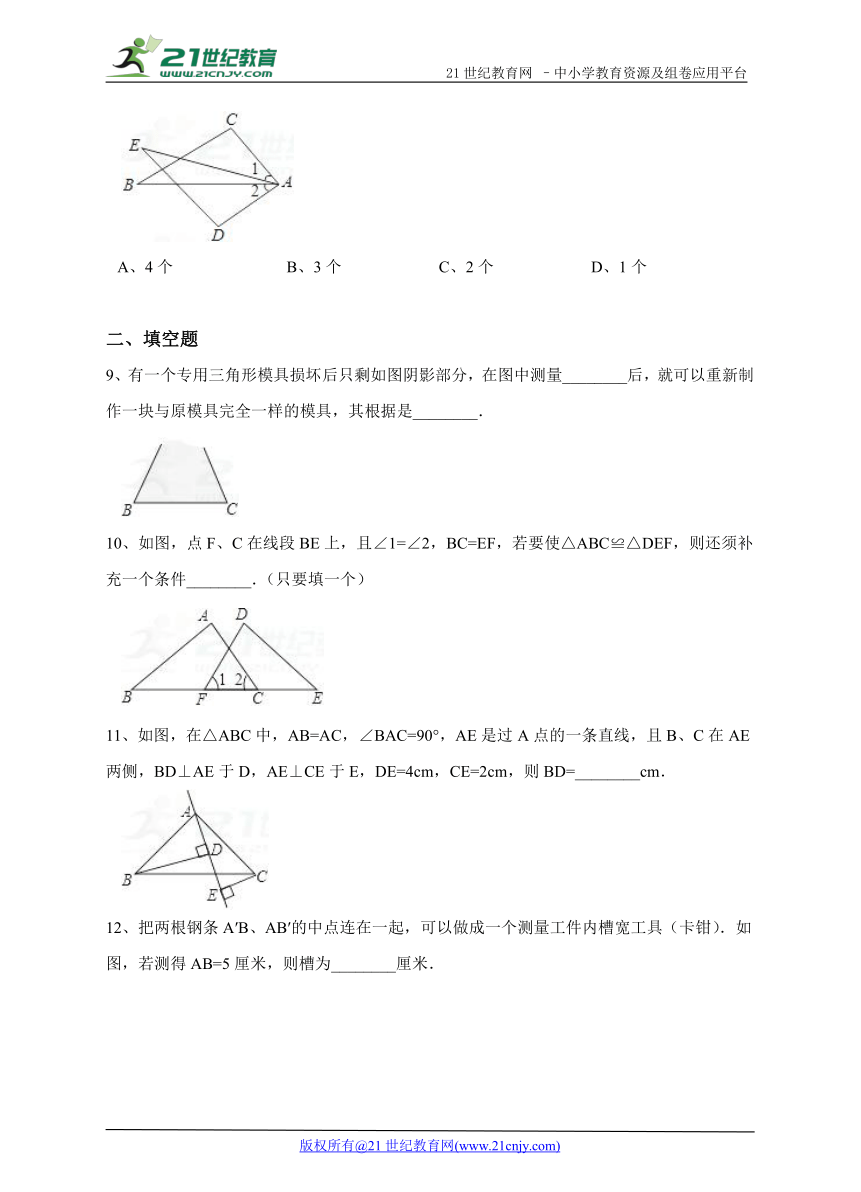
A、4个 B、3个 C、2个 D、1个
二、填空题
9、有一个专用三角形模具损坏后只剩如图阴影部分,在图中测量________后,就可以重新制作一块与原模具完全一样的模具,其根据是________.
10、如图,点F、C在线段BE上,且∠1=∠2,BC=EF,若要使△ABC≌△DEF,则还须补充一个条件________.(只要填一个)
11、如图,在△ABC中,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在AE两侧,BD⊥AE于D,AE⊥CE于E,DE=4cm,CE=2cm,则BD=________cm.
12、把两根钢条A′B、AB′的中点连在一起,可以做成一个测量工件内槽宽工具(卡钳).如图,若测得AB=5厘米,则槽为________厘米.21*cnjy*com
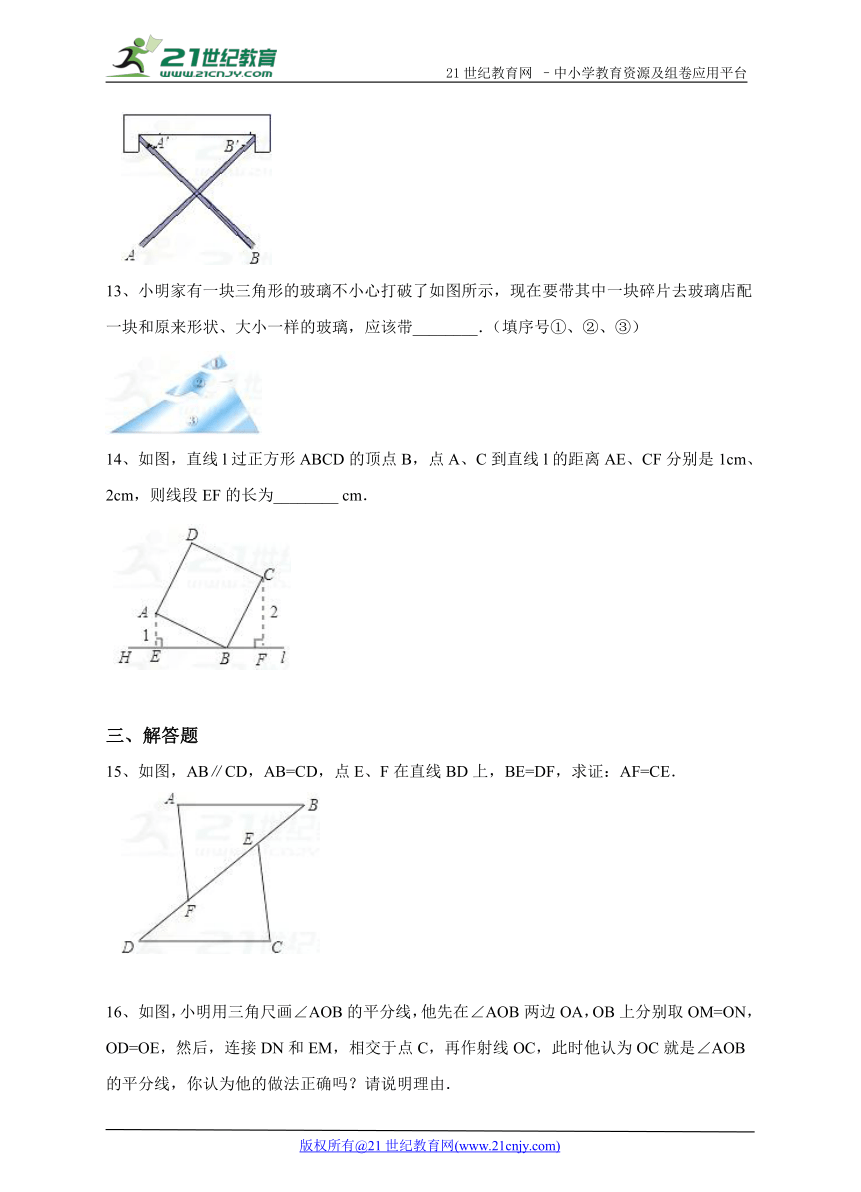
13、小明家有一块三角形的玻璃不小心打破了如图所示,现在要带其中一块碎片去玻璃店配一块和原来形状、大小一样的玻璃,应该带________.(填序号①、②、③)
14、如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离AE、CF分别是1cm、2cm,则线段EF的长为________ cm.
三、解答题
15、如图,AB∥CD,AB=CD,点E、F在直线BD上,BE=DF,求证:AF=CE.
16、如图,小明用三角尺画∠AOB的平分线,他先在∠AOB两边OA,OB上分别取OM=ON,OD=OE,然后,连接DN和EM,相交于点C,再作射线OC,此时他认为OC就是∠AOB的平分线,你认为他的做法正确吗?请说明理由.2-1-c-n-j-y
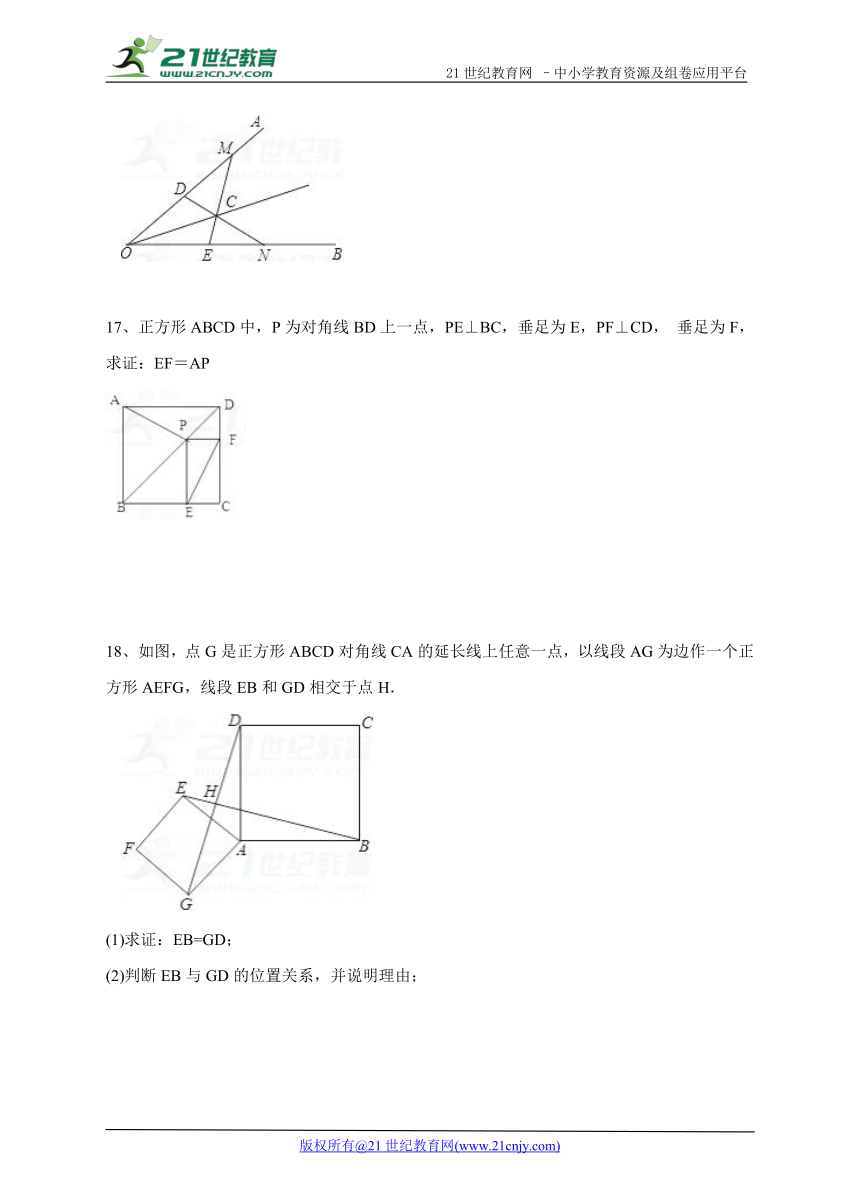
17、正方形ABCD中,P为对角线BD上一点,PE⊥BC,垂足为E,PF⊥CD, 垂足为F,求证:EF=AP
21cnjy.com
18、如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.【出处:21教育名师】
(1)求证:EB=GD;
(2)判断EB与GD的位置关系,并说明理由;
参考答案与试题解析
一、单选题
1、D
解:∵四边形ABCD是平行四边形,∴AB=CD,AD=BC;OD=OB,OA=OC;
∵在△AOD和△COB中2·1·c·n·j·y
∴△AOD≌△COB(SAS);
同理可得出△AOB≌△COD(SAS);
∵在△ABD和△DCB中21*cnjy*com
,
∴△ABD≌△CDB(SSS);
同理可得:△ACD≌△CAB(SSS).
共有4对全等三角形.
故选D.
【版权所有:21教育】
2、D
解:连接CE、DE,
在△OCE和△ODE中,
,
∴△OCE≌△ODE(SSS),
∴∠AOE=∠BOE.
因此画∠AOB的平分线OE,其理论依据是:SSS.
故选:D.
3、C
解:∵四边形ABCD是正方形, ∴BC=CD,∠BCD=∠DCF=90°,
∵在△BCE和△DCF中
,
∴△BCE≌△DCF,
∴∠DFC=∠BEC=80°,
∵∠DCF=90°,CE=CF,
∴∠CFE=∠CEF=45°,
∴∠EFD=80°﹣45°=35°.
故选C.
4、A
解:∵BF=CE,
∴BC=EF,且AC=FD,
∴当∠E=∠B时,是“SSA”,故①不能;
当AC∥DF时,可得∠ACB=∠DFE,满足“SAS”,故②可以;
当∠A=∠D时,是“SSA”,故③不能;
综上可知能说明△ABC≌△DEF的有1个,
故选A.
5、C
解: ∵AB=DE,
∴当BC=EC,∠B=∠E时,满足SAS,可证明△ABC≌△DEC,故A可以;
当BC=EC,AC=DC时,满足SSS,可证明△ABC≌△DEC,故B可以;
当BC=DC,∠A=∠D时,在△ABC中是ASS,在△DEC中是SAS,故不能证明△ABC≌△DEC,故C不可以;
当AC=DC,∠A=∠D时,满足SAS,可证明△ABC≌△DEC,故D可以;
故选C.
21·世纪*教育网
6、D
解:∵全等三角形的判定定理有SAS,ASA,AAS,SSS, SSS定理即三边对应相等的两个三角形全等,∴①正确;
∵三角对应相等的两个三角形不全等,∴②错误;
∵两边和它们的夹角对应相等的两个三角形全等,∴③正确;
∵两角及其中一角的对边对应相等的两个三角形全等,∴④正确;
∵两边及其中一边的对角对应相等的两个三角形不全等,∴⑤错误;
故选D.
21·cn·jy·com
7、D
解:∵AB=AC,AC≠BC,AH⊥BC于H,BD⊥AC于D,CE⊥AB于E, ∴BH=CH,∠BAH=∠CAH,∠ABC=∠ACB,BC=CB,AH=AH,
∴Rt△ABH≌Rt△ACH,Rt△BCE≌Rt△CBD,
∴BE=CD,
∴AE=AD,
∴Rt△AEO≌Rt△ADO,Rt△EOB≌Rt△DOC,Rt△ABD≌Rt△AEC,
∴OB=OC,
∴Rt△OHB≌Rt△OHC.
∴共有6对全等直角三角形.
故选D.
【来源:21·世纪·教育·网】
8、B
解:已知∠1=∠2,AC=AD,由∠1=∠2可知∠BAC=∠EAD, 加①AB=AE,就可以用SAS判定△ABC≌△AED;
加③∠C=∠D,就可以用ASA判定△ABC≌△AED;
加④∠B=∠E,就可以用AAS判定△ABC≌△AED;
加②BC=ED只是具备SSA,不能判定三角形全等.
其中能使△ABC≌△AED的条件有:①③④
故选:B.
二、填空题
9、∠B、∠C、BC;ASA
解:测量出∠B、∠C、BC,根据是ASA. 故答案为:∠B、∠C、BC;ASA
10、AC=DF
解:补充AC=DF. ∵∠1=∠2,BC=EF,AC=DF
∴△ABC≌△DEF,
故填AC=DF.
11、6
解:∵BD⊥AE于D,AE⊥CE于E,∠BAC=90° ∠BDA=∠AEC=90°,∠EAC+∠ACE=90°,∠EAC+∠BAD=90°
∴∠BAD=∠ACE
在△ABD与△CAE中
∴△ABD≌△CAE(AAS)
∴AD=CE,BD=AE
∵DE=4cm,CE=2cm
∴AE=AD+DE=CE+DE=6cm
∴BD=6cm.
12、5
解:连接AB, ∵把两根钢条A′B、AB′的中点连在一起,
∴AO=A′O,BO=B′O,
在△ABO和△A′B′O中
,
∴△AOB≌△A′OB′(SAS),
∴A′B′=AB=5cm,
故答案为:5.
13、③
解:第①块,仅保留了原三角形的一个角和部分边,不符合任何判定方法; 第②块,仅保留了原三角形的一部分边,所以该块不行;
第③块,不但保留了原三角形的两个角还保留了其中一个边,所以符合ASA判定,所以应该拿这块去.
故答案为:③.
21教育网
14、3
解:∵四边形ABCD为正方形, ∴AB=BC,∠ABC=90°.
∵AE⊥l,CF⊥l,
∴∠E=∠F=90°,∠EAB+∠ABE=90°,∠FBC+∠BCF=90°.
∵∠ABE+∠ABC+∠FBC=180°,
∴∠ABE+∠FBC=90°,
∴∠EAB=∠FBC.
在△ABE和△BCF中,
,
∴△ABE≌△BCF(AAS),
∴BE=CF=2cm,BF=AE=1cm,
∴EF=BE+BF=2+1=3cm.
故答案为:3.
www.21-cn-jy.com
三、解答题
15、证明:∵DF=BE, ∴DF+EF=BE+EF,
即:CE=BF,
∵AB∥CD,
∴∠AEB=∠CFD,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴AF=CE.
16、解:他的做法正确; 理由:在△MOE和△NOD中
∴△MOE≌△NOD(SAS),
∴∠OME=∠DNO,
∵OM=ON,OD=OE,
∴DM=EN,
∴在△MDC和△NEC中
∴△MDC≌△NEC(AAS),
∴DC=EC,
在△DOC和△EOC中
∴△DOC≌△EOC(SSS),
∴∠DOC=∠EOC,
∴OC就是∠AOB的平分线.
21世纪教育网版权所有
17、证明:分别延长FP、EP交AB于F',AD于E',
可知四边形BEPF'和FPE′D是正方形,
∴PE=PF'=AE',PF=PE'.且∠AE'P=∠EPF.
∴△APE'≌△EFP.
∴AP=EF.
www-2-1-cnjy-com
18、(1)证明:在△GAD和△EAB中,∠GAD=90°+∠EAD,∠EAB=90°+∠EAD ∴∠GAD=∠EAB,
∵四边形EFGA和四边形ABCD是正方形,
∴AG=AE,AB=AD,
在△GAD和△EAB中,
∴△GAD≌△EAB(SAS),
∴EB=GD;
(2)解:EB⊥GD.
理由如下:∵四边形ABCD是正方形,
∴∠DAB=90°,∴∠AMB+∠ABM=90°,
又∵△AEB≌△AGD,∴∠GDA=∠EBA,
∵∠HMD=∠AMB(对顶角相等),
∴∠HDM+∠DMH=∠AMB+∠ABM=90°,
∴∠DHM=180°﹣(∠HDM+∠DMH)=180°﹣90°=90°,
∴EB⊥GD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
新人教版八年级数学上册同步练习
12.2三角形全等的判定
一、单选题
1、如图,在平行四边形ABCD中,连接对角线AC、BD,图中的全等三角形的对数( )
A、1对 B、2对 C、3对 D、4对
2、如图,用直尺和圆规画∠AOB的平分线OE,其理论依据是( )
A、SAS B、ASA C、AAS D、SSS
3、如图,正方形ABCD中,E为CD边上一点,F为BC延长线上一点,CE=CF.若∠BEC=80°,则∠EFD的度数为( )【来源:21cnj*y.co*m】
A、20° B、25° C、35° D、40°
4、如图,在△ABC与△DEF中,B、F、C、E在一条直线上,若BF=CE,AC=FD,则下列补充的条件能说明△ABC≌△DEF的有( ) ①∠E=∠B; ②AC∥DF; ③∠A=∠D.
A、1个 B、2个 C、3个 D、0个
5、如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A、BC=EC,∠B=∠E B、BC=EC,AC=DC
C、BC=DC,∠A=∠D D、AC=DC,∠A=∠D
6、下列说法中: ①三边对应相等的两个三角形全等;
②三角对应相等的两个三角形全等;
③两边和它们的夹角对应相等的两个三角形全等;
④两角及其中一角的对边对应相等的两个三角形全等;
⑤两边及其中一边的对角对应相等的两个三角形全等;
其中不正确的是( )
A、①② B、②④ C、④⑤ D、②⑤
7、如图,AB=AC,AC≠BC,AH⊥BC于H,BD⊥AC于D,CE⊥AB于E,AH、BD、CE交于O,图中全等直角三角形的对数( )
A、3 B、4 C、5 D、6
8、如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的条件有( )21教育名师原创作品
A、4个 B、3个 C、2个 D、1个
二、填空题
9、有一个专用三角形模具损坏后只剩如图阴影部分,在图中测量________后,就可以重新制作一块与原模具完全一样的模具,其根据是________.
10、如图,点F、C在线段BE上,且∠1=∠2,BC=EF,若要使△ABC≌△DEF,则还须补充一个条件________.(只要填一个)
11、如图,在△ABC中,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在AE两侧,BD⊥AE于D,AE⊥CE于E,DE=4cm,CE=2cm,则BD=________cm.
12、把两根钢条A′B、AB′的中点连在一起,可以做成一个测量工件内槽宽工具(卡钳).如图,若测得AB=5厘米,则槽为________厘米.21*cnjy*com
13、小明家有一块三角形的玻璃不小心打破了如图所示,现在要带其中一块碎片去玻璃店配一块和原来形状、大小一样的玻璃,应该带________.(填序号①、②、③)
14、如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离AE、CF分别是1cm、2cm,则线段EF的长为________ cm.
三、解答题
15、如图,AB∥CD,AB=CD,点E、F在直线BD上,BE=DF,求证:AF=CE.
16、如图,小明用三角尺画∠AOB的平分线,他先在∠AOB两边OA,OB上分别取OM=ON,OD=OE,然后,连接DN和EM,相交于点C,再作射线OC,此时他认为OC就是∠AOB的平分线,你认为他的做法正确吗?请说明理由.2-1-c-n-j-y
17、正方形ABCD中,P为对角线BD上一点,PE⊥BC,垂足为E,PF⊥CD, 垂足为F,求证:EF=AP
21cnjy.com
18、如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.【出处:21教育名师】
(1)求证:EB=GD;
(2)判断EB与GD的位置关系,并说明理由;
参考答案与试题解析
一、单选题
1、D
解:∵四边形ABCD是平行四边形,∴AB=CD,AD=BC;OD=OB,OA=OC;
∵在△AOD和△COB中2·1·c·n·j·y
∴△AOD≌△COB(SAS);
同理可得出△AOB≌△COD(SAS);
∵在△ABD和△DCB中21*cnjy*com
,
∴△ABD≌△CDB(SSS);
同理可得:△ACD≌△CAB(SSS).
共有4对全等三角形.
故选D.
【版权所有:21教育】
2、D
解:连接CE、DE,
在△OCE和△ODE中,
,
∴△OCE≌△ODE(SSS),
∴∠AOE=∠BOE.
因此画∠AOB的平分线OE,其理论依据是:SSS.
故选:D.
3、C
解:∵四边形ABCD是正方形, ∴BC=CD,∠BCD=∠DCF=90°,
∵在△BCE和△DCF中
,
∴△BCE≌△DCF,
∴∠DFC=∠BEC=80°,
∵∠DCF=90°,CE=CF,
∴∠CFE=∠CEF=45°,
∴∠EFD=80°﹣45°=35°.
故选C.
4、A
解:∵BF=CE,
∴BC=EF,且AC=FD,
∴当∠E=∠B时,是“SSA”,故①不能;
当AC∥DF时,可得∠ACB=∠DFE,满足“SAS”,故②可以;
当∠A=∠D时,是“SSA”,故③不能;
综上可知能说明△ABC≌△DEF的有1个,
故选A.
5、C
解: ∵AB=DE,
∴当BC=EC,∠B=∠E时,满足SAS,可证明△ABC≌△DEC,故A可以;
当BC=EC,AC=DC时,满足SSS,可证明△ABC≌△DEC,故B可以;
当BC=DC,∠A=∠D时,在△ABC中是ASS,在△DEC中是SAS,故不能证明△ABC≌△DEC,故C不可以;
当AC=DC,∠A=∠D时,满足SAS,可证明△ABC≌△DEC,故D可以;
故选C.
21·世纪*教育网
6、D
解:∵全等三角形的判定定理有SAS,ASA,AAS,SSS, SSS定理即三边对应相等的两个三角形全等,∴①正确;
∵三角对应相等的两个三角形不全等,∴②错误;
∵两边和它们的夹角对应相等的两个三角形全等,∴③正确;
∵两角及其中一角的对边对应相等的两个三角形全等,∴④正确;
∵两边及其中一边的对角对应相等的两个三角形不全等,∴⑤错误;
故选D.
21·cn·jy·com
7、D
解:∵AB=AC,AC≠BC,AH⊥BC于H,BD⊥AC于D,CE⊥AB于E, ∴BH=CH,∠BAH=∠CAH,∠ABC=∠ACB,BC=CB,AH=AH,
∴Rt△ABH≌Rt△ACH,Rt△BCE≌Rt△CBD,
∴BE=CD,
∴AE=AD,
∴Rt△AEO≌Rt△ADO,Rt△EOB≌Rt△DOC,Rt△ABD≌Rt△AEC,
∴OB=OC,
∴Rt△OHB≌Rt△OHC.
∴共有6对全等直角三角形.
故选D.
【来源:21·世纪·教育·网】
8、B
解:已知∠1=∠2,AC=AD,由∠1=∠2可知∠BAC=∠EAD, 加①AB=AE,就可以用SAS判定△ABC≌△AED;
加③∠C=∠D,就可以用ASA判定△ABC≌△AED;
加④∠B=∠E,就可以用AAS判定△ABC≌△AED;
加②BC=ED只是具备SSA,不能判定三角形全等.
其中能使△ABC≌△AED的条件有:①③④
故选:B.
二、填空题
9、∠B、∠C、BC;ASA
解:测量出∠B、∠C、BC,根据是ASA. 故答案为:∠B、∠C、BC;ASA
10、AC=DF
解:补充AC=DF. ∵∠1=∠2,BC=EF,AC=DF
∴△ABC≌△DEF,
故填AC=DF.
11、6
解:∵BD⊥AE于D,AE⊥CE于E,∠BAC=90° ∠BDA=∠AEC=90°,∠EAC+∠ACE=90°,∠EAC+∠BAD=90°
∴∠BAD=∠ACE
在△ABD与△CAE中
∴△ABD≌△CAE(AAS)
∴AD=CE,BD=AE
∵DE=4cm,CE=2cm
∴AE=AD+DE=CE+DE=6cm
∴BD=6cm.
12、5
解:连接AB, ∵把两根钢条A′B、AB′的中点连在一起,
∴AO=A′O,BO=B′O,
在△ABO和△A′B′O中
,
∴△AOB≌△A′OB′(SAS),
∴A′B′=AB=5cm,
故答案为:5.
13、③
解:第①块,仅保留了原三角形的一个角和部分边,不符合任何判定方法; 第②块,仅保留了原三角形的一部分边,所以该块不行;
第③块,不但保留了原三角形的两个角还保留了其中一个边,所以符合ASA判定,所以应该拿这块去.
故答案为:③.
21教育网
14、3
解:∵四边形ABCD为正方形, ∴AB=BC,∠ABC=90°.
∵AE⊥l,CF⊥l,
∴∠E=∠F=90°,∠EAB+∠ABE=90°,∠FBC+∠BCF=90°.
∵∠ABE+∠ABC+∠FBC=180°,
∴∠ABE+∠FBC=90°,
∴∠EAB=∠FBC.
在△ABE和△BCF中,
,
∴△ABE≌△BCF(AAS),
∴BE=CF=2cm,BF=AE=1cm,
∴EF=BE+BF=2+1=3cm.
故答案为:3.
www.21-cn-jy.com
三、解答题
15、证明:∵DF=BE, ∴DF+EF=BE+EF,
即:CE=BF,
∵AB∥CD,
∴∠AEB=∠CFD,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴AF=CE.
16、解:他的做法正确; 理由:在△MOE和△NOD中
∴△MOE≌△NOD(SAS),
∴∠OME=∠DNO,
∵OM=ON,OD=OE,
∴DM=EN,
∴在△MDC和△NEC中
∴△MDC≌△NEC(AAS),
∴DC=EC,
在△DOC和△EOC中
∴△DOC≌△EOC(SSS),
∴∠DOC=∠EOC,
∴OC就是∠AOB的平分线.
21世纪教育网版权所有
17、证明:分别延长FP、EP交AB于F',AD于E',
可知四边形BEPF'和FPE′D是正方形,
∴PE=PF'=AE',PF=PE'.且∠AE'P=∠EPF.
∴△APE'≌△EFP.
∴AP=EF.
www-2-1-cnjy-com
18、(1)证明:在△GAD和△EAB中,∠GAD=90°+∠EAD,∠EAB=90°+∠EAD ∴∠GAD=∠EAB,
∵四边形EFGA和四边形ABCD是正方形,
∴AG=AE,AB=AD,
在△GAD和△EAB中,
∴△GAD≌△EAB(SAS),
∴EB=GD;
(2)解:EB⊥GD.
理由如下:∵四边形ABCD是正方形,
∴∠DAB=90°,∴∠AMB+∠ABM=90°,
又∵△AEB≌△AGD,∴∠GDA=∠EBA,
∵∠HMD=∠AMB(对顶角相等),
∴∠HDM+∠DMH=∠AMB+∠ABM=90°,
∴∠DHM=180°﹣(∠HDM+∠DMH)=180°﹣90°=90°,
∴EB⊥GD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
