2017—2018学年数学湘教版九年级上册第3章图形的相似 单元测试(含答案)
文档属性
| 名称 | 2017—2018学年数学湘教版九年级上册第3章图形的相似 单元测试(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 222.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-17 00:00:00 | ||
图片预览


文档简介
单元测试(三) 图形的相似
(时间:45分钟 满分:100分)
一、选择题(每小题3分,共24分)
1.已知=,那么下列各式中,不成立的是(
)
A.2x=3y
B.3x=2y
C.=
D.=
2.在比例尺为1∶5
000的地图上,量得甲、乙两地的距离为25
cm,则甲、乙两地间的实际距离是(
)
A.1
250
km
B.125
km
C.12.5
km
D.1.25
km
3.(南京中考)若△ABC∽△A′B′C′,相似比为1∶2,则△ABC与△A′B′C′的面积的比为(
)
A.1∶2
B.2∶1
C.1∶4
D.4∶1
4.某学习小组在讨论“变化的三角形”时,知道大三角形与小三角形是位似图形(如图所示),则小三角形上的顶点(a,b)对应于大三角形上的顶点坐标为(
)
A.(-2a,-2b)
B.(2a,2b)
C.(-2b,-2a)
D.(-2a,-b)
5.如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是(
)
A.AB2=BC·BD
B.AB2=AC·BD
C.AB·AD=BD·BC
D.AB·AD=AD·CD
6.(毕节中考)如图,△ABC中,AE交BC于点D,∠C=∠E,AD∶DE=3∶5,AE=8,BD=4,则DC的长等于(
)
A.
B.
C.
D.
7.如图,在钝角△ABC中,AB=6
cm,AC=12
cm,动点D从A点出发到B点止,动点E从C点出发到A点止,点D运动的速度为1
cm/秒,点E运动的速度为2
cm/秒.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是(
)
A.3秒或4.8秒
B.3秒
C.4.5秒
D.4.5秒或4.8秒
8.如图,已知△ABC、△DEA是两个全等的等腰直角三角形,∠BAC=∠D=90°,两条直角边AB、AD重合,把AD绕点A逆时针旋转α角(0°<α<90°),到如图所示的位置时,BC分别与AD、AE相交于点F、G,则图中相似三角形的对数为(
)
A.1对
B.2对
C.3对
D.4对
二、填空题(每小题4分,共32分)
9.已知=,则=________.
10.已知线段a、b、c、d成比例,且a=6,b=9,c=12,则d=________.
11.若两个相似三角形的相似比是2∶3,则这两个三角形对应中线的比是________.
12.如图,直线l1∥l2∥l3,已知AG=0.6
cm,BG=1.2
cm,CD=1.5
cm,则CH=________cm.
13.(温州一模)若△ABC∽△A′B′C′且=,△ABC的周长为15
cm,则△A′B′C′的周长为________cm.
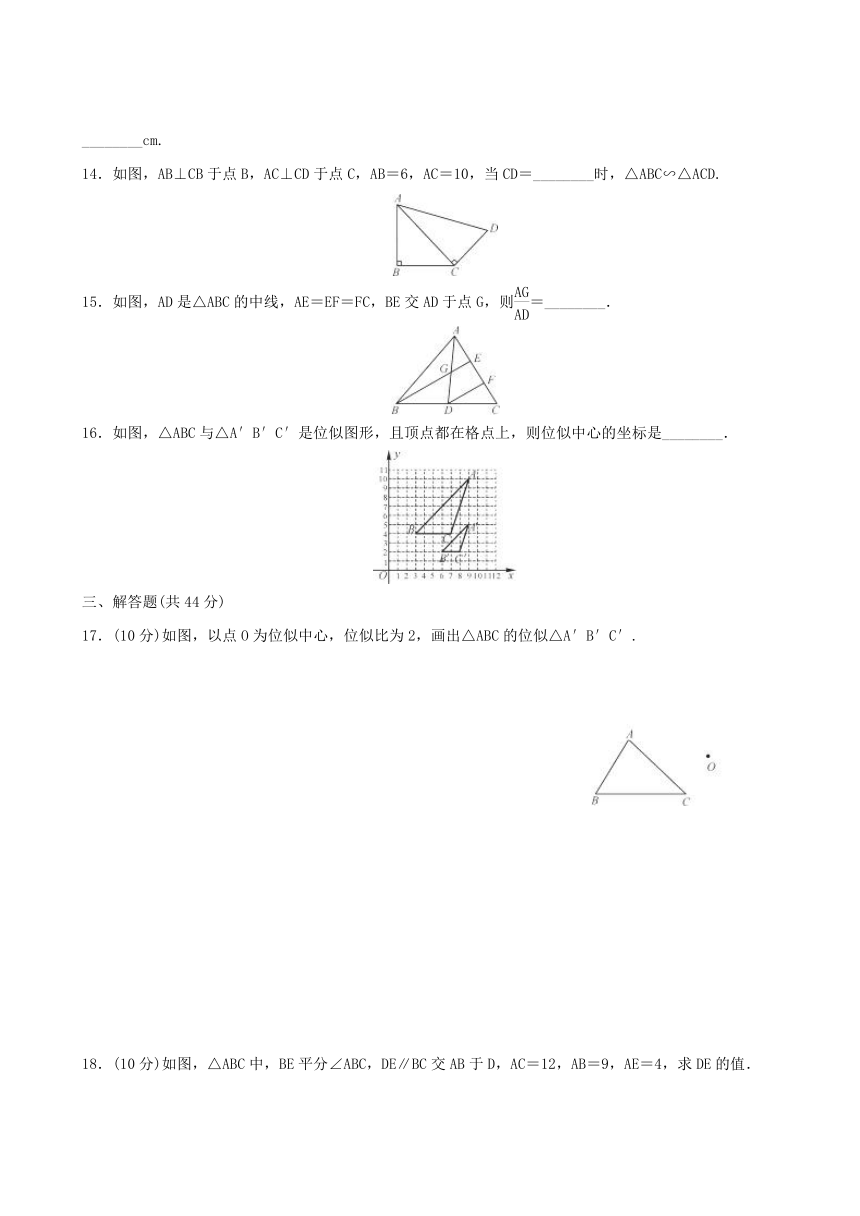
14.如图,AB⊥CB于点B,AC⊥CD于点C,AB=6,AC=10,当CD=________时,△ABC∽△ACD.
15.如图,AD是△ABC的中线,AE=EF=FC,BE交AD于点G,则=________.
16.如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,则位似中心的坐标是________.
三、解答题(共44分)
17.(10分)如图,以点O为位似中心,位似比为2,画出△ABC的位似△A′B′C′.
18.(10分)如图,△ABC中,BE平分∠ABC,DE∥BC交AB于D,AC=12,AB=9,AE=4,求DE的值.
19.(12分)如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
20.(12分)(泰安中考)如图,在四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
(1)求证:AC2=AB·AD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求的值.
参考答案
1.B 2.D 3.C 4.A 5.A 6.A 7.A 8.D 9. 10.18 11.2∶3 12.0.5 13.20 14. 15. 16.(9,0)
17如图.
18.∵BE平分∠ABC,∴∠ABE=∠EBC.
∵DE∥BC,∴∠EBC=∠DEB.∴∠ABE=∠DEB.∴BD=ED.
设DE=x,则BD=x,AD=9-x.
∵DE∥BC,∴=,即=,解得x=6.∴DE=6.
19.变短了.
∵∠MAC=∠MOP=90°,∠AMC=∠OMP,
∴△MAC∽△MOP.∴=,即=.解得MA=5.
同理由△NBD∽△NOP可求得NB=1.5.MA-NB=5-1.5=3.5(米).即小明的身影变短了3.5米.
20.(1)∵AC平分∠DAB,∴∠DAC=∠CAB.
又∵∠ADC=∠ACB=90°,∴△ADC∽△ACB.∴=,即AC2=AB·AD.
(2)∵∠ACB=90°,E为AB的中点,∴CE=AB=AE,∴∠EAC=∠ECA.
又∵∠CAD=∠CAB.∴∠DAC=∠ECA.∴CE∥AD.
(3)∵CE∥AD,∴△AFD∽△CFE.∴=.
∵CE=AB=×6=3,AD=4,
∴=.∴=,即=.
(时间:45分钟 满分:100分)
一、选择题(每小题3分,共24分)
1.已知=,那么下列各式中,不成立的是(
)
A.2x=3y
B.3x=2y
C.=
D.=
2.在比例尺为1∶5
000的地图上,量得甲、乙两地的距离为25
cm,则甲、乙两地间的实际距离是(
)
A.1
250
km
B.125
km
C.12.5
km
D.1.25
km
3.(南京中考)若△ABC∽△A′B′C′,相似比为1∶2,则△ABC与△A′B′C′的面积的比为(
)
A.1∶2
B.2∶1
C.1∶4
D.4∶1
4.某学习小组在讨论“变化的三角形”时,知道大三角形与小三角形是位似图形(如图所示),则小三角形上的顶点(a,b)对应于大三角形上的顶点坐标为(
)
A.(-2a,-2b)
B.(2a,2b)
C.(-2b,-2a)
D.(-2a,-b)
5.如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是(
)
A.AB2=BC·BD
B.AB2=AC·BD
C.AB·AD=BD·BC
D.AB·AD=AD·CD
6.(毕节中考)如图,△ABC中,AE交BC于点D,∠C=∠E,AD∶DE=3∶5,AE=8,BD=4,则DC的长等于(
)
A.
B.
C.
D.
7.如图,在钝角△ABC中,AB=6
cm,AC=12
cm,动点D从A点出发到B点止,动点E从C点出发到A点止,点D运动的速度为1
cm/秒,点E运动的速度为2
cm/秒.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是(
)
A.3秒或4.8秒
B.3秒
C.4.5秒
D.4.5秒或4.8秒
8.如图,已知△ABC、△DEA是两个全等的等腰直角三角形,∠BAC=∠D=90°,两条直角边AB、AD重合,把AD绕点A逆时针旋转α角(0°<α<90°),到如图所示的位置时,BC分别与AD、AE相交于点F、G,则图中相似三角形的对数为(
)
A.1对
B.2对
C.3对
D.4对
二、填空题(每小题4分,共32分)
9.已知=,则=________.
10.已知线段a、b、c、d成比例,且a=6,b=9,c=12,则d=________.
11.若两个相似三角形的相似比是2∶3,则这两个三角形对应中线的比是________.
12.如图,直线l1∥l2∥l3,已知AG=0.6
cm,BG=1.2
cm,CD=1.5
cm,则CH=________cm.
13.(温州一模)若△ABC∽△A′B′C′且=,△ABC的周长为15
cm,则△A′B′C′的周长为________cm.
14.如图,AB⊥CB于点B,AC⊥CD于点C,AB=6,AC=10,当CD=________时,△ABC∽△ACD.
15.如图,AD是△ABC的中线,AE=EF=FC,BE交AD于点G,则=________.
16.如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,则位似中心的坐标是________.
三、解答题(共44分)
17.(10分)如图,以点O为位似中心,位似比为2,画出△ABC的位似△A′B′C′.
18.(10分)如图,△ABC中,BE平分∠ABC,DE∥BC交AB于D,AC=12,AB=9,AE=4,求DE的值.
19.(12分)如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
20.(12分)(泰安中考)如图,在四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
(1)求证:AC2=AB·AD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求的值.
参考答案
1.B 2.D 3.C 4.A 5.A 6.A 7.A 8.D 9. 10.18 11.2∶3 12.0.5 13.20 14. 15. 16.(9,0)
17如图.
18.∵BE平分∠ABC,∴∠ABE=∠EBC.
∵DE∥BC,∴∠EBC=∠DEB.∴∠ABE=∠DEB.∴BD=ED.
设DE=x,则BD=x,AD=9-x.
∵DE∥BC,∴=,即=,解得x=6.∴DE=6.
19.变短了.
∵∠MAC=∠MOP=90°,∠AMC=∠OMP,
∴△MAC∽△MOP.∴=,即=.解得MA=5.
同理由△NBD∽△NOP可求得NB=1.5.MA-NB=5-1.5=3.5(米).即小明的身影变短了3.5米.
20.(1)∵AC平分∠DAB,∴∠DAC=∠CAB.
又∵∠ADC=∠ACB=90°,∴△ADC∽△ACB.∴=,即AC2=AB·AD.
(2)∵∠ACB=90°,E为AB的中点,∴CE=AB=AE,∴∠EAC=∠ECA.
又∵∠CAD=∠CAB.∴∠DAC=∠ECA.∴CE∥AD.
(3)∵CE∥AD,∴△AFD∽△CFE.∴=.
∵CE=AB=×6=3,AD=4,
∴=.∴=,即=.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
