2017—2018学年数学湘教版九年级上册第3章图形的相似 章末复习(含答案)
文档属性
| 名称 | 2017—2018学年数学湘教版九年级上册第3章图形的相似 章末复习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 243.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-17 19:24:17 | ||
图片预览

文档简介
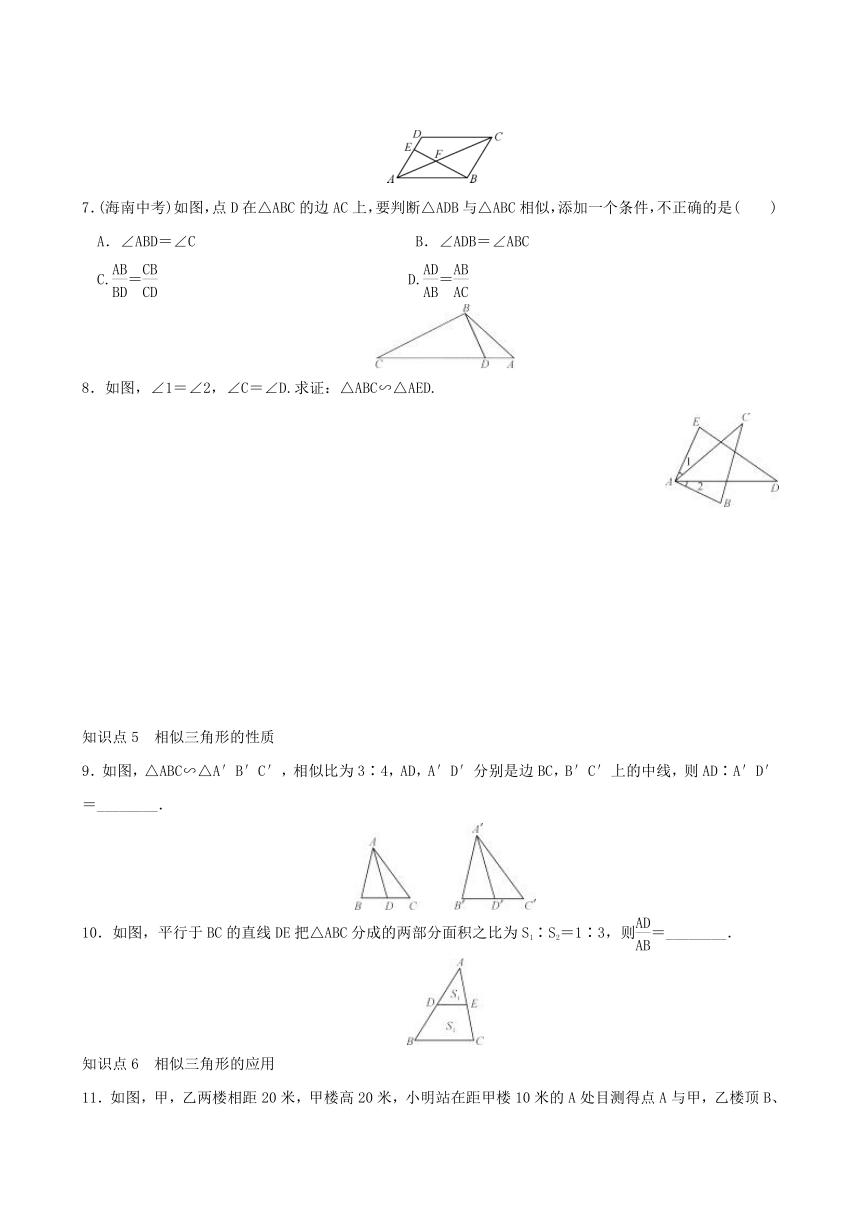
章末复习(三) 图形的相似
基础题
知识点1 比例及比例线段
1.下列各线段的长度成比例的是(
)
A.2
cm,5
cm,6
cm,8
cm
B.1
cm,2
cm,3
cm,4
cm
C.3
cm,6
cm,7
cm,9
cm
D.3
cm,6
cm,9
cm,18
cm
2.已知5x-8y=0,则x∶y=________.
知识点2 平行线分线段成比例
3.如图,已知AB∥CD∥EF,那么下列结论正确的是(
)
A.=
B.=
C.=
D.=
知识点3 相似图形和位似图形
4.如图所示,它们是两个相似的平行四边形,根据条件可知,∠α=________,m=________.
5.如图,将△AOB缩小得到△COD,则△AOB与△COD的相似比是________.
知识点4 相似三角形的判定
6.如图,在
□ABCD中,E为AD的三等分点,AE=AD,连接BE,交AC于点F,AC=12,则AF为(
)
A.4
B.4.8
C.5.2
D.6
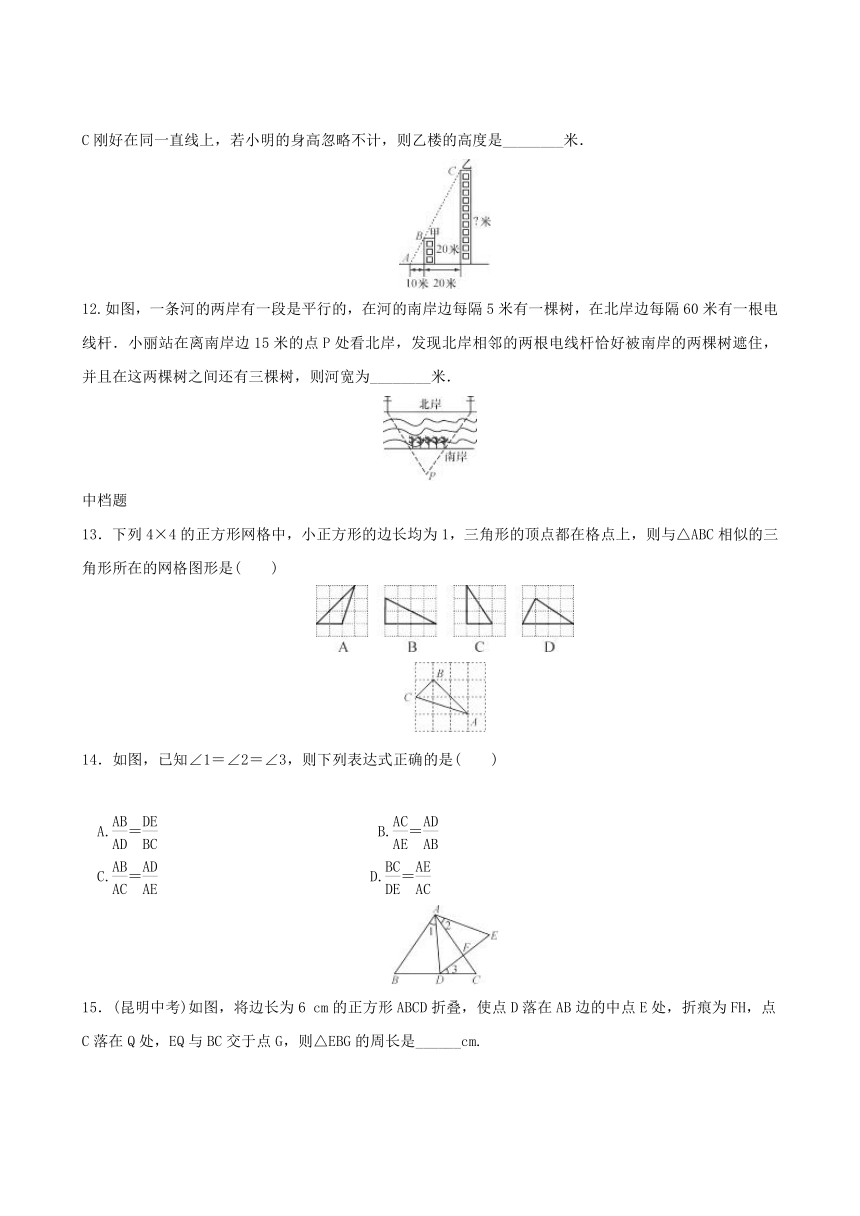
7.(海南中考)如图,点D在△ABC的边AC上,要判断△ADB与△ABC相似,添加一个条件,不正确的是(
)
A.∠ABD=∠C
B.∠ADB=∠ABC
C.=
D.=
8.如图,∠1=∠2,∠C=∠D.求证:△ABC∽△AED.
知识点5 相似三角形的性质
9.如图,△ABC∽△A′B′C′,相似比为3∶4,AD,A′D′分别是边BC,B′C′上的中线,则AD∶A′D′=________.
10.如图,平行于BC的直线DE把△ABC分成的两部分面积之比为S1∶S2=1∶3,则=________.
知识点6 相似三角形的应用
11.如图,甲,乙两楼相距20米,甲楼高20米,小明站在距甲楼10米的A处目测得点A与甲,乙楼顶B、C刚好在同一直线上,若小明的身高忽略不计,则乙楼的高度是________米.
12.如图,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔60米有一根电线杆.小丽站在离南岸边15米的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为________米.
中档题
13.下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是(
)
14.如图,已知∠1=∠2=∠3,则下列表达式正确的是(
)
A.=
B.=
C.=
D.=
15.(昆明中考)如图,将边长为6
cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,则△EBG的周长是______cm.
16.在△ABC中,∠B=25°,AD是BC边上的高,并且AD2=BD·DC,则∠BCA的度数为________.
17.如图,在正方形ABCD中,E为CD的中点,F在BC上,且BF=3FC,求的值.
18.(牡丹江中考改编)在同一时刻两根木杆在太阳光下的影子如图所示,其中木杆AB=2
m,它的影子BC=1.6
m,木杆PQ的影子有一部分落在了墙上,PM=1.2
m,MN=0.8
m,求木杆PQ的长度.
综合题
19.(益阳中考改编)如图,在△ABC中,AB=AC,BD=CD,CE⊥AB
于E.BE=2,BC=6.
(1)求证:△ABD∽△CBE;
(2)求AE的长度;
(3)设AD与CE交于F,求△CFD的面积.
参考答案
基础题
1.D 2.8∶5 3.A 4.125° 12 5.2∶1 6.B 7.C
8.∵∠1=∠2,∴∠1+∠CAD=∠2+∠CAD,即∠BAC=∠EAD.又∵∠C=∠D,∴△ABC∽△AED.
9.3∶4 10. 11.60 12.30
中档题
13.B 14.C 15.2 16.65°或115°
17.设FC=a,∵BF=3FC=3a,则BC=4a.
∵E为CD的中点,∴DE=EC=2a.
∵==2,==2,∴=.
∵∠ADE=∠ECF=90°,∴△ADE∽△ECF.∴===.
18.过N点作ND⊥PQ于D,∴=.
又∵AB=2,BC=1.6,PM=1.2,NM=0.8,∴QD==1.5.
∴PQ=QD+DP=QD+NM=1.5+0.8=2.3(米).
答:木杆PQ的长度为2.3米.
综合题
19.(1)在△ABC中,AB=AC,BD=CD,∴AD⊥BC.∵CE⊥AB,∴∠ADB=∠CEB=90°.
又∠B=∠B,∴△ABD∽△CBE.
(2)∵△ABD∽△CBE,∴AB∶CB=BD∶BE.∴AB∶6=3∶2.解得AB=9.∴AE=7.
(3)在Rt△BEC中,由勾股定理得CE=4.、
∵∠ADC=∠CEB=90°,∠ECB=∠ECB,
∴△CDF∽△CEB.
∴CD∶CE=DF∶BE.
∴3∶4=DF∶2.
解得DF=.
∴△CFD的面积为××3=.
基础题
知识点1 比例及比例线段
1.下列各线段的长度成比例的是(
)
A.2
cm,5
cm,6
cm,8
cm
B.1
cm,2
cm,3
cm,4
cm
C.3
cm,6
cm,7
cm,9
cm
D.3
cm,6
cm,9
cm,18
cm
2.已知5x-8y=0,则x∶y=________.
知识点2 平行线分线段成比例
3.如图,已知AB∥CD∥EF,那么下列结论正确的是(
)
A.=
B.=
C.=
D.=
知识点3 相似图形和位似图形
4.如图所示,它们是两个相似的平行四边形,根据条件可知,∠α=________,m=________.
5.如图,将△AOB缩小得到△COD,则△AOB与△COD的相似比是________.
知识点4 相似三角形的判定
6.如图,在
□ABCD中,E为AD的三等分点,AE=AD,连接BE,交AC于点F,AC=12,则AF为(
)
A.4
B.4.8
C.5.2
D.6
7.(海南中考)如图,点D在△ABC的边AC上,要判断△ADB与△ABC相似,添加一个条件,不正确的是(
)
A.∠ABD=∠C
B.∠ADB=∠ABC
C.=
D.=
8.如图,∠1=∠2,∠C=∠D.求证:△ABC∽△AED.
知识点5 相似三角形的性质
9.如图,△ABC∽△A′B′C′,相似比为3∶4,AD,A′D′分别是边BC,B′C′上的中线,则AD∶A′D′=________.
10.如图,平行于BC的直线DE把△ABC分成的两部分面积之比为S1∶S2=1∶3,则=________.
知识点6 相似三角形的应用
11.如图,甲,乙两楼相距20米,甲楼高20米,小明站在距甲楼10米的A处目测得点A与甲,乙楼顶B、C刚好在同一直线上,若小明的身高忽略不计,则乙楼的高度是________米.
12.如图,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔60米有一根电线杆.小丽站在离南岸边15米的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为________米.
中档题
13.下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是(
)
14.如图,已知∠1=∠2=∠3,则下列表达式正确的是(
)
A.=
B.=
C.=
D.=
15.(昆明中考)如图,将边长为6
cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,则△EBG的周长是______cm.
16.在△ABC中,∠B=25°,AD是BC边上的高,并且AD2=BD·DC,则∠BCA的度数为________.
17.如图,在正方形ABCD中,E为CD的中点,F在BC上,且BF=3FC,求的值.
18.(牡丹江中考改编)在同一时刻两根木杆在太阳光下的影子如图所示,其中木杆AB=2
m,它的影子BC=1.6
m,木杆PQ的影子有一部分落在了墙上,PM=1.2
m,MN=0.8
m,求木杆PQ的长度.
综合题
19.(益阳中考改编)如图,在△ABC中,AB=AC,BD=CD,CE⊥AB
于E.BE=2,BC=6.
(1)求证:△ABD∽△CBE;
(2)求AE的长度;
(3)设AD与CE交于F,求△CFD的面积.
参考答案
基础题
1.D 2.8∶5 3.A 4.125° 12 5.2∶1 6.B 7.C
8.∵∠1=∠2,∴∠1+∠CAD=∠2+∠CAD,即∠BAC=∠EAD.又∵∠C=∠D,∴△ABC∽△AED.
9.3∶4 10. 11.60 12.30
中档题
13.B 14.C 15.2 16.65°或115°
17.设FC=a,∵BF=3FC=3a,则BC=4a.
∵E为CD的中点,∴DE=EC=2a.
∵==2,==2,∴=.
∵∠ADE=∠ECF=90°,∴△ADE∽△ECF.∴===.
18.过N点作ND⊥PQ于D,∴=.
又∵AB=2,BC=1.6,PM=1.2,NM=0.8,∴QD==1.5.
∴PQ=QD+DP=QD+NM=1.5+0.8=2.3(米).
答:木杆PQ的长度为2.3米.
综合题
19.(1)在△ABC中,AB=AC,BD=CD,∴AD⊥BC.∵CE⊥AB,∴∠ADB=∠CEB=90°.
又∠B=∠B,∴△ABD∽△CBE.
(2)∵△ABD∽△CBE,∴AB∶CB=BD∶BE.∴AB∶6=3∶2.解得AB=9.∴AE=7.
(3)在Rt△BEC中,由勾股定理得CE=4.、
∵∠ADC=∠CEB=90°,∠ECB=∠ECB,
∴△CDF∽△CEB.
∴CD∶CE=DF∶BE.
∴3∶4=DF∶2.
解得DF=.
∴△CFD的面积为××3=.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
