13.3.2 等边三角形课件
图片预览






文档简介
课件23张PPT。等边三角形观察下列图片,你有
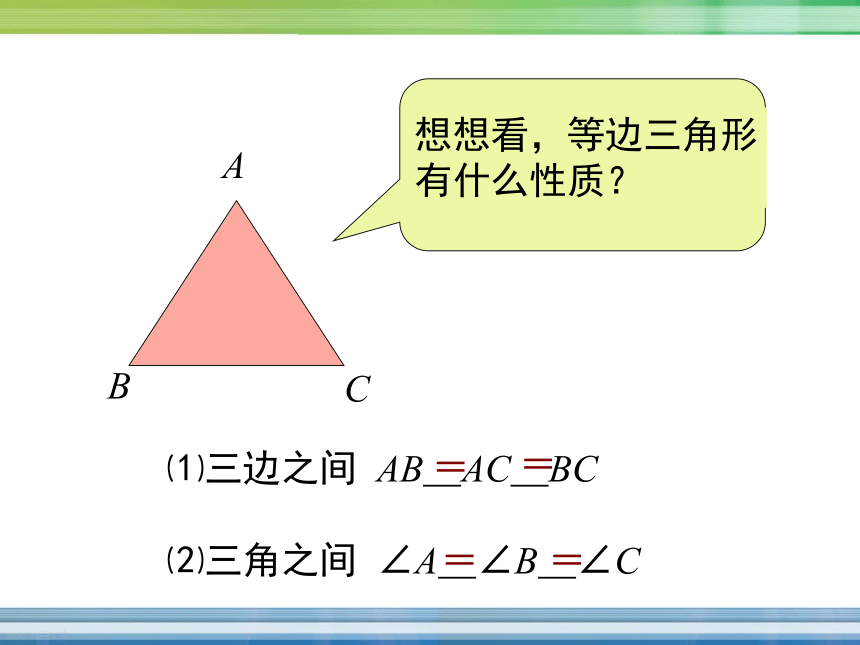
什么印象?你发现了什么?这就是今天我们要学的等边三角形ABC⑴三边之间 AB_AC_BC
⑵三角之间 ∠A_∠B_∠C====⑵ 等边三角形的三个内角都相等,并且
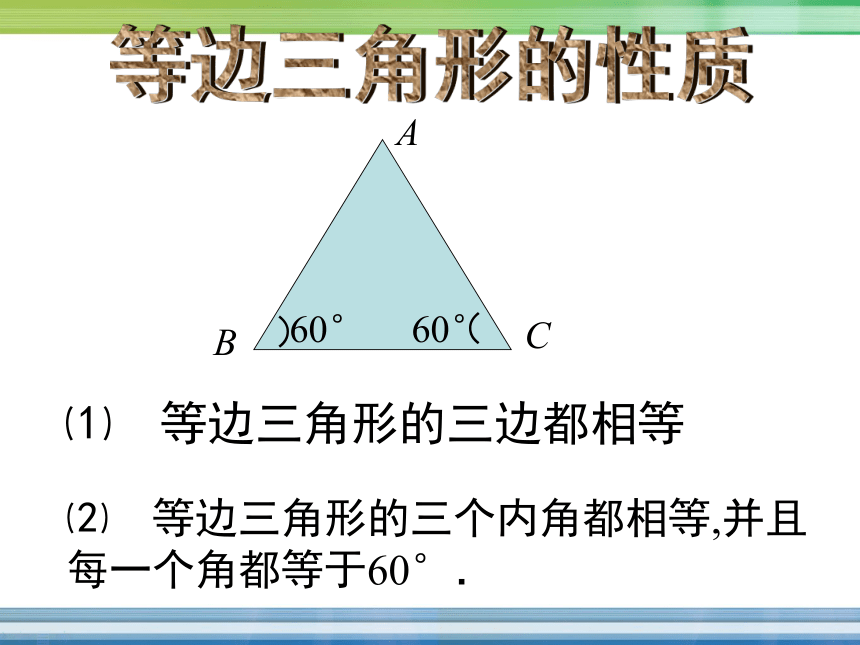
每一个角都等于60°.等边三角形的性质⑴ 等边三角形的三边都相等 符号语言:
∵ △ABC 是等边三角形,
∴ ∠A =∠B =∠C =60°.细心观察,探索性质 等边三角形的性质:
等边三角形的三个内角都相等,并且每一个角都等
于60°. 相等
每个角都等于60°细心观察,探索性质 结合等腰三角形的性质,你能填出等边三角形对应
的结论吗? 是(三线合一)
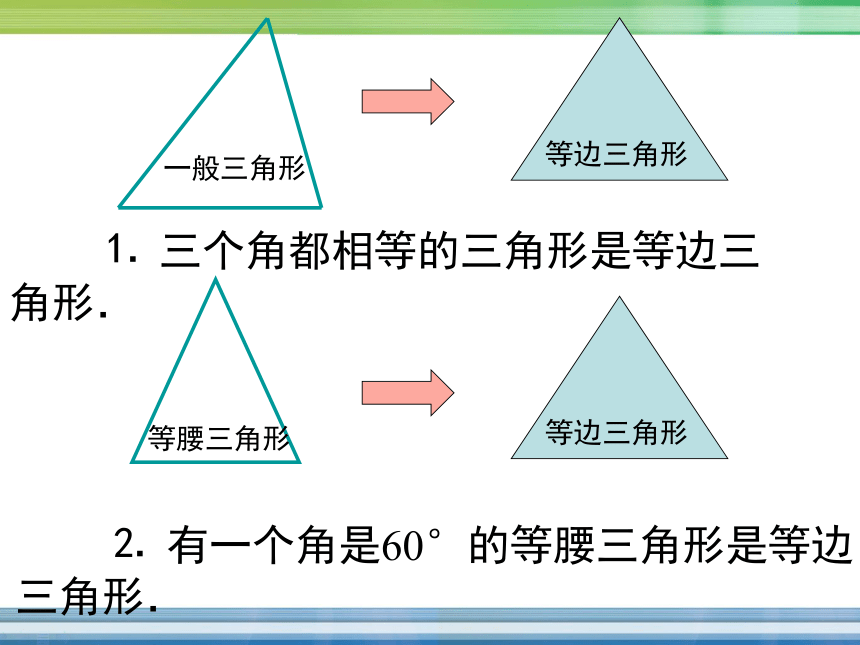
三条对称轴思考题? 一个三角形满足什么条件
就是等边三角形? ⒈ 三个角都相等的三角形是等边三角形. ⒉ 有一个角是60°的等腰三角形是等边
三角形.符号语言:
在△ABC 中,
∵ ∠A=∠B =∠C ,
∴ △ABC 是等边三角形.细心观察,探索性质 等边三角形的判定定理1:
三个角都相等的三角形是等边三角形. 细心观察,探索性质 等边三角形的判定定理2:
有一个角为60°的等腰三角形是等边三角形. 符号语言:
在△ABC 中,
∵ BC =AC,∠A =60°,
∴ △ABC 是等边三角形. 证明: ∵ △ABC 是等边三角形,
∴ ∠A =∠B =∠C =60°.
∵ DE∥BC,
∴ ∠B =∠ADE,∠C =∠AED.
∴ ∠A=∠ADE =∠AED.
∴ △ADE 是等边三角形.动脑思考,例题解析 例1 如图,△ABC 是等边三角形,DE∥BC, 分
别交AB,AC 于点D,E.求证:△ADE 是等边三角形. 追问 本题还有其他证法吗? 将两个含有板有30°的三角尺如图摆放在
一起你能借助这个图形,找到Rt△ABC的直角
边BC与斜边AB之间的数量关系吗?
探究∵△ABC与△ADC关于AC轴对称
∴AB=AD
△ABD是等边三角形
又∵AC⊥BD∴BC=DC=1/2AB动手操作,探索性质另证:
在△ACE 中,
∵ ∠A=30°,∠ACE =30°,
∴ △AEC是等腰三角形.
∴ CE =AE.
∴ BC =BE =CE =AE.符号语言:
∵ 在Rt△ABC 中,
∠C =90°,∠A =30°, 动手操作,探索性质 在直角三角形中,如果一个锐角等于30°,那么
它所对的直角边等于斜边的一半.5课堂练习 练习1 如图,在△ABC 中,∠C =90°,∠A =
30°,AB =10,则BC 的长为 .1课堂练习 练习2 如图,在△ABC 中,∠ACB =90°,CD 是
高,∠A =30°,AB =4.则BD = . 解:∵ DE⊥AC,BC⊥AC,∠A =30°,∴ BC =3.7(m). 答:立柱BC 的长是3.7 m,DE 的长是1.85 m. 性质运用 例 如图是屋架设计图的一部分,点D 是斜梁AB
的中点,立柱BC、DE 垂直于横梁AC,AB =7.4 cm,
∠A =30°,立柱BC、DE 要多长? 要把一块三角形的土地均匀分给甲 、 乙、丙三家农户去种植,如果∠C=90°∠B=30°,要使这三家农户所得土地的大小和形状都相同,请你试着分一分,在图上画出来.请你分一分 这是两个等边三角形,那么请移动三根火
柴,将此图变成四个等边三角形. 提示:此题并不难,如果外部不能解决,那么
想想里面吧.考考你小结 我们这节课学习了哪些知识?
谈谈你的体会.再见
什么印象?你发现了什么?这就是今天我们要学的等边三角形ABC⑴三边之间 AB_AC_BC
⑵三角之间 ∠A_∠B_∠C====⑵ 等边三角形的三个内角都相等,并且
每一个角都等于60°.等边三角形的性质⑴ 等边三角形的三边都相等 符号语言:
∵ △ABC 是等边三角形,
∴ ∠A =∠B =∠C =60°.细心观察,探索性质 等边三角形的性质:
等边三角形的三个内角都相等,并且每一个角都等
于60°. 相等
每个角都等于60°细心观察,探索性质 结合等腰三角形的性质,你能填出等边三角形对应
的结论吗? 是(三线合一)
三条对称轴思考题? 一个三角形满足什么条件
就是等边三角形? ⒈ 三个角都相等的三角形是等边三角形. ⒉ 有一个角是60°的等腰三角形是等边
三角形.符号语言:
在△ABC 中,
∵ ∠A=∠B =∠C ,
∴ △ABC 是等边三角形.细心观察,探索性质 等边三角形的判定定理1:
三个角都相等的三角形是等边三角形. 细心观察,探索性质 等边三角形的判定定理2:
有一个角为60°的等腰三角形是等边三角形. 符号语言:
在△ABC 中,
∵ BC =AC,∠A =60°,
∴ △ABC 是等边三角形. 证明: ∵ △ABC 是等边三角形,
∴ ∠A =∠B =∠C =60°.
∵ DE∥BC,
∴ ∠B =∠ADE,∠C =∠AED.
∴ ∠A=∠ADE =∠AED.
∴ △ADE 是等边三角形.动脑思考,例题解析 例1 如图,△ABC 是等边三角形,DE∥BC, 分
别交AB,AC 于点D,E.求证:△ADE 是等边三角形. 追问 本题还有其他证法吗? 将两个含有板有30°的三角尺如图摆放在
一起你能借助这个图形,找到Rt△ABC的直角
边BC与斜边AB之间的数量关系吗?
探究∵△ABC与△ADC关于AC轴对称
∴AB=AD
△ABD是等边三角形
又∵AC⊥BD∴BC=DC=1/2AB动手操作,探索性质另证:
在△ACE 中,
∵ ∠A=30°,∠ACE =30°,
∴ △AEC是等腰三角形.
∴ CE =AE.
∴ BC =BE =CE =AE.符号语言:
∵ 在Rt△ABC 中,
∠C =90°,∠A =30°, 动手操作,探索性质 在直角三角形中,如果一个锐角等于30°,那么
它所对的直角边等于斜边的一半.5课堂练习 练习1 如图,在△ABC 中,∠C =90°,∠A =
30°,AB =10,则BC 的长为 .1课堂练习 练习2 如图,在△ABC 中,∠ACB =90°,CD 是
高,∠A =30°,AB =4.则BD = . 解:∵ DE⊥AC,BC⊥AC,∠A =30°,∴ BC =3.7(m). 答:立柱BC 的长是3.7 m,DE 的长是1.85 m. 性质运用 例 如图是屋架设计图的一部分,点D 是斜梁AB
的中点,立柱BC、DE 垂直于横梁AC,AB =7.4 cm,
∠A =30°,立柱BC、DE 要多长? 要把一块三角形的土地均匀分给甲 、 乙、丙三家农户去种植,如果∠C=90°∠B=30°,要使这三家农户所得土地的大小和形状都相同,请你试着分一分,在图上画出来.请你分一分 这是两个等边三角形,那么请移动三根火
柴,将此图变成四个等边三角形. 提示:此题并不难,如果外部不能解决,那么
想想里面吧.考考你小结 我们这节课学习了哪些知识?
谈谈你的体会.再见
