2017—2018学年数学北师大版必修2第1章立体几何初步章末测试
文档属性
| 名称 | 2017—2018学年数学北师大版必修2第1章立体几何初步章末测试 |

|
|
| 格式 | zip | ||
| 文件大小 | 292.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-19 00:00:00 | ||
图片预览



文档简介
第一章章末测试
班级____ 姓名____ 考号____ 分数____
本试卷满分100分,考试时间90分钟.
一、选择题:本大题共10小题,每小题4分,共40分.在下列各题的四个选项中,只有一个选项是符合题目要求的.
1.若a α,b β,α∩β=c,a∩b=M,则( )
A.M∈c
B.M c
C.M c
D.M c
答案:A
解析:注意点、线、面关系的符号表示,结合平面的公理3可知,M∈c.
2.从长方体的一个顶点引出的三条棱的长度分别是2,3,3,则长方体的外接球的表面积为( )
A.20π
B.22π
C.24π
D.26π
答案:B
解析:设球的半径为r,则4r2=22+32+32=22,球的表面积为4πr2=22π.
3.一个几何体的三视图中的正(主)视图、侧(左)视图、俯视图均是大小形状完全相同的图形,那么这个几何体可能是( )
A.圆柱
B.圆锥
C.圆台
D.球
答案:D
解析:因为球的三视图都是半径相等的圆,则其他的三个均不可能满足条件.
4.圆锥的高伸长为原来的2倍,底面半径缩小为原来的,则它的体积是原来体积的( )
A.
B.
C.
D.
答案:A
解析:设原圆锥高为h,底面面积为S,则V=hS,新圆锥的高为2h,底面面积为,∴V′=×2h×=V.
5.如图,已知正方体ABCD-A1B1C1D1,E是DD1的中点,F是BB1的中点,设过点C1,E,F三点的平面为α,则正方体被平面α所截的截面的形状为( )
A.菱形
B.矩形
C.梯形
D.五边形
答案:A
解析:设正方体棱长为a,连接AE,C1F易发现AE∥C1F,所以平面α经过点A,所以截面是四边形AEC1F,根据勾股定理易求得AE=EC1=C1F=AF=a,所以截面为菱形.
6.平面α与平面β平行的条件可以是( )
A.α内有无数条直线都与平面β平行
B.α内的任何直线都与平面β平行
C.直线a α,直线b β且a∥β,b∥α
D.直线a∥α,a∥β
答案:B
7.底面是正三角形,侧棱垂直底面水平放置的三棱柱的所有棱长均为2,当其正(主)视图有最大面积时,其侧(左)视图的面积为( )
A.2
B.
C.2
D.6
答案:C
解析:S=×2=2.
8.设α、β是两个不同的平面,a、b是两条不同的直线,给出下列四个命题,其中正确的命题是( )
A.若a∥α,b∥α,则a∥b
B.若a∥α,b∥β,a∥b,则α∥β
C.若a⊥α,b⊥β,a⊥b,则α⊥β
D.若a、b在平面α内的射影互相垂直,则a⊥b
答案:C
解析:与同一平面平行的两条直线不一定平行,所以A错误;与两条平行直线分别平行的两个平面未必平行,所以B错误;如图所示,直线a,b在平面α内的射影分别为m、n,显然m⊥n,但a、b不垂直,所以D错误,故选C.
9.三条直线a、b、c两两平行且不共面,这三条直线可以确定m个平面,这m个平面把空间分成n个部分,则( )
A.m=2,n=2
B.m=2,n=6
C.m=3,n=7
D.m=3,n=8
答案:C
解析:本题主要考查空间想象能力,三条不共面的平行线可以确定三个平面,而这三个平面把空间分成7部分.
10.平行六面体的相交于一顶点的三条棱长分别是a、b、c,三条棱中每两条的夹角都是60°,则它的体积是( )
A.abc
B.
C.abc
D.abc
答案:D
解析:如图所示,设AA1=c,AB=a,AD=b,A1在底面射影O.
在∠DAB的平分线上,作OE⊥AB于E,连结A1E,则A1E⊥AB,在Rt△A1AE中,∠A1AE=60°,AE=,
在Rt△AEO中,∠OAE=30°,AO=c,高A1O=c.
∴V=S四边形ABCD·A1O=abc.
二、填空题:本大题共3小题,每小题4分,共12分.把答案填在题中横线上.
11.正方体的内切球与外接球的体积之比等于________.
答案:1:3
解析:设正方体的棱长为a,则内切球半径为r=,外接球半径R=a.
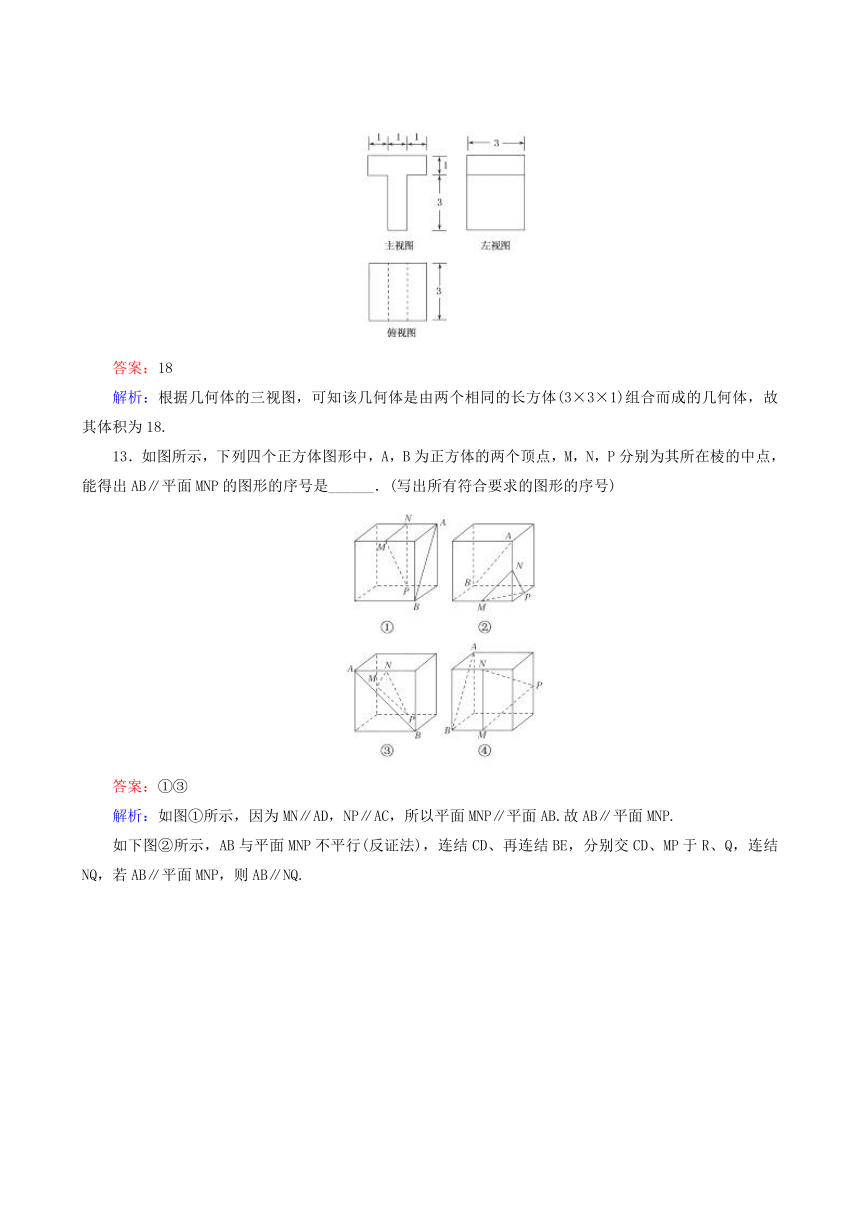
12.若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是________cm3.
答案:18
解析:根据几何体的三视图,可知该几何体是由两个相同的长方体(3×3×1)组合而成的几何体,故其体积为18.
13.如图所示,下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是______.(写出所有符合要求的图形的序号)
答案:①③
解析:如图①所示,因为MN∥AD,NP∥AC,所以平面MNP∥平面AB.故AB∥平面MNP.
如下图②所示,AB与平面MNP不平行(反证法),连结CD、再连结BE,分别交CD、MP于R、Q,连结NQ,若AB∥平面MNP,则AB∥NQ.
又由N为AE的中点,R为BE的中点,得AB∥NR.在平面ABE中过点N有两条相交的直线平行于AB,与平行公理矛盾,所以AB与平面MNP不平行.
如图③所示,连结CD,因为AD平行且等于BC,所以四边形ABCD为平行四边形.所以AB∥CD.又因为MP∥CD,所以AB∥MP.所以AB∥平面MNP.
对于④,AB与平面MNP不平行(反证法),如上图④所示,连接DM,ME.若AB∥平面MNP,因为MN∥DP,所以DM 平面MNP,又DM 平面ABMD,所以AB∥DM.又由AD平行且等于BC,得四边形ABCD是平行四边形,故AB∥CD.在平面ABCD中过点D有两条相交直线平行于AB,与平行公理矛盾.于是AB与平面MNP不平行.
三、解答题:本大题共5小题,共48分,其中第14小题8分,第15~18小题各10分.解答应写出文字说明、证明过程或演算步骤.
14.四棱锥P-ABCD中,底面ABCD是矩形,PD⊥底面ABCD,AD=PD,E、F分别为CD、PB的中点,求证:EF⊥面PAB.
证明:
如图,连结EP.
∵PD⊥面ABCD,DE在面ABCD内,
∴PD⊥DE,又CE=ED,PD=AD=BC.
∴Rt△BCE≌Rt△PDE.∴PE=BE.
∵F为PB的中点,∴EF⊥PB,
∵PD⊥ABCD
AB ABCD
∴PD⊥AB
又∵AB⊥AD∴AB⊥平面PAD∴PA⊥AB
∴在Rt△PAB中,PF=AF,又PE=BE=EA,
∴△EFP≌△EFA,∴EF⊥FA.
又PB,FA为平面PAB内相交直线
∴EF⊥面PAB.
15.
如图所示,在正三角形ABC中,E、F分别是AB、AC的中点,AD⊥BC,EH⊥BC,FG⊥BC,D、H、G为垂足,若将正△ABC绕AD旋转一周所得圆锥体积为V,求由阴影部分所产生旋转体的体积与V的比值.
解:
如图所示,设圆锥的高为h,底面半径为r,则圆柱的高为,底半径为,则=1-=1-=1-=.
16.如图所示,在侧棱垂直于底面ABC的三棱柱ABC-A1B1C1中,
A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F是B1C1的中点.求证:
(1)平面ADE⊥平面BCC1B1;
(2)直线A1F∥平面ADE.
证明:(1)因为CC1⊥平面ABC,又AD 平面ABC,所以CC1⊥AD.
又因为AD⊥DE,CC1,DE 平面BCC1B1,CC1∩DE=E,所以AD⊥平面BCC1B1.又AD 平面ADE,
所以平面ADE⊥平面BCC1B1.
(2)因为A1B1=A1C1,F为B1C1的中点,所以A1F⊥B1C1.
因为CC1⊥平面A1B1C1,且A1F 平面A1B1C1,所以CC1⊥A1F.
又因为CC1,B1C1 平面BCC1B1,CC1∩B1C1=C1,所以A1F⊥平面BCC1B1.
由(1)知AD⊥平面BCC1B1,所以A1F∥AD.
又AD 平面ADE,A1F 平面ADE,所以A1F∥平面ADE.
17.如图所示,AB是圆柱的母线,O′是上底面的圆心,△BCD是下底面圆的内接三角形,且BD是下底面圆的直径,E是CD的中点.求证:
(1)O′E∥平面ABC;
(2)平面O′CD⊥平面ABC.
解:
(1)取BC中点为F,连结EF,O′A,
则EF是△BCD的中位线,
∴EF綊BD.
设下底面圆心为O,连结OO′,∵AB是母线,
∴AB綊OO′,
∴AO′綊EF,
∴AF∥O′E且AF 平面ABC,O′E 平面ABC,
∴O′E∥平面ABC.
(2)在圆柱中,AB⊥平面BCD,∴AB⊥CD
∵BC⊥CD,AB∩BC=B
∴CD⊥平面ABC
∵CD 平面O′CD
∴平面O′CD⊥平面ABC.
18.如图所示,在侧面均垂直于底面ABC的三棱柱ABC-A′B′C′中,∠BAC=90°,AB=AC=,AA′=1,点M,N分别为A′B和B′C′的中点.
(1)证明:MN∥平面A′ACC′;
(2)求三棱锥A′-MNC的体积.
解:
(1)(法一)连接AB′,AC′,由已知∠BAC=90°,AB=AC,三棱柱ABC-A′B′C′为直三棱柱,所以M为AB′中点.
又因为N为B′C′的中点,
所以MN∥AC′.
又MN 平面A′ACC′,
AC′ 平面A′ACC′,
因此MN∥平面A′ACC′.
(法二)取A′B′中点P,连接MP,NP,
则M,N分别为AB′与B′C′的中点,所以MP∥AA′,PN∥A′C′,
所以MP∥平面A′ACC′,PN∥平面A′ACC′.
又MP∩NP=P,因此平面MPN∥平面A′ACC′.
而MN 平面MPN,因此MN∥平面A′ACC′.
(2)(法一)连接BN,由题意A′N⊥B′C′,平面A′B′C′∩平面B′BCC′=B′C′,
所以A′N⊥平面NBC.
又A′N=B′C′=1,故VA′-MNC=VN-A′MC=VN-A′BC=VA′-NBC=.
(法二)VA′-MNC=VA′-NBC-VM-NBC
=VA′-NBC=.
班级____ 姓名____ 考号____ 分数____
本试卷满分100分,考试时间90分钟.
一、选择题:本大题共10小题,每小题4分,共40分.在下列各题的四个选项中,只有一个选项是符合题目要求的.
1.若a α,b β,α∩β=c,a∩b=M,则( )
A.M∈c
B.M c
C.M c
D.M c
答案:A
解析:注意点、线、面关系的符号表示,结合平面的公理3可知,M∈c.
2.从长方体的一个顶点引出的三条棱的长度分别是2,3,3,则长方体的外接球的表面积为( )
A.20π
B.22π
C.24π
D.26π
答案:B
解析:设球的半径为r,则4r2=22+32+32=22,球的表面积为4πr2=22π.
3.一个几何体的三视图中的正(主)视图、侧(左)视图、俯视图均是大小形状完全相同的图形,那么这个几何体可能是( )
A.圆柱
B.圆锥
C.圆台
D.球
答案:D
解析:因为球的三视图都是半径相等的圆,则其他的三个均不可能满足条件.
4.圆锥的高伸长为原来的2倍,底面半径缩小为原来的,则它的体积是原来体积的( )
A.
B.
C.
D.
答案:A
解析:设原圆锥高为h,底面面积为S,则V=hS,新圆锥的高为2h,底面面积为,∴V′=×2h×=V.
5.如图,已知正方体ABCD-A1B1C1D1,E是DD1的中点,F是BB1的中点,设过点C1,E,F三点的平面为α,则正方体被平面α所截的截面的形状为( )
A.菱形
B.矩形
C.梯形
D.五边形
答案:A
解析:设正方体棱长为a,连接AE,C1F易发现AE∥C1F,所以平面α经过点A,所以截面是四边形AEC1F,根据勾股定理易求得AE=EC1=C1F=AF=a,所以截面为菱形.
6.平面α与平面β平行的条件可以是( )
A.α内有无数条直线都与平面β平行
B.α内的任何直线都与平面β平行
C.直线a α,直线b β且a∥β,b∥α
D.直线a∥α,a∥β
答案:B
7.底面是正三角形,侧棱垂直底面水平放置的三棱柱的所有棱长均为2,当其正(主)视图有最大面积时,其侧(左)视图的面积为( )
A.2
B.
C.2
D.6
答案:C
解析:S=×2=2.
8.设α、β是两个不同的平面,a、b是两条不同的直线,给出下列四个命题,其中正确的命题是( )
A.若a∥α,b∥α,则a∥b
B.若a∥α,b∥β,a∥b,则α∥β
C.若a⊥α,b⊥β,a⊥b,则α⊥β
D.若a、b在平面α内的射影互相垂直,则a⊥b
答案:C
解析:与同一平面平行的两条直线不一定平行,所以A错误;与两条平行直线分别平行的两个平面未必平行,所以B错误;如图所示,直线a,b在平面α内的射影分别为m、n,显然m⊥n,但a、b不垂直,所以D错误,故选C.
9.三条直线a、b、c两两平行且不共面,这三条直线可以确定m个平面,这m个平面把空间分成n个部分,则( )
A.m=2,n=2
B.m=2,n=6
C.m=3,n=7
D.m=3,n=8
答案:C
解析:本题主要考查空间想象能力,三条不共面的平行线可以确定三个平面,而这三个平面把空间分成7部分.
10.平行六面体的相交于一顶点的三条棱长分别是a、b、c,三条棱中每两条的夹角都是60°,则它的体积是( )
A.abc
B.
C.abc
D.abc
答案:D
解析:如图所示,设AA1=c,AB=a,AD=b,A1在底面射影O.
在∠DAB的平分线上,作OE⊥AB于E,连结A1E,则A1E⊥AB,在Rt△A1AE中,∠A1AE=60°,AE=,
在Rt△AEO中,∠OAE=30°,AO=c,高A1O=c.
∴V=S四边形ABCD·A1O=abc.
二、填空题:本大题共3小题,每小题4分,共12分.把答案填在题中横线上.
11.正方体的内切球与外接球的体积之比等于________.
答案:1:3
解析:设正方体的棱长为a,则内切球半径为r=,外接球半径R=a.
12.若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是________cm3.
答案:18
解析:根据几何体的三视图,可知该几何体是由两个相同的长方体(3×3×1)组合而成的几何体,故其体积为18.
13.如图所示,下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是______.(写出所有符合要求的图形的序号)
答案:①③
解析:如图①所示,因为MN∥AD,NP∥AC,所以平面MNP∥平面AB.故AB∥平面MNP.
如下图②所示,AB与平面MNP不平行(反证法),连结CD、再连结BE,分别交CD、MP于R、Q,连结NQ,若AB∥平面MNP,则AB∥NQ.
又由N为AE的中点,R为BE的中点,得AB∥NR.在平面ABE中过点N有两条相交的直线平行于AB,与平行公理矛盾,所以AB与平面MNP不平行.
如图③所示,连结CD,因为AD平行且等于BC,所以四边形ABCD为平行四边形.所以AB∥CD.又因为MP∥CD,所以AB∥MP.所以AB∥平面MNP.
对于④,AB与平面MNP不平行(反证法),如上图④所示,连接DM,ME.若AB∥平面MNP,因为MN∥DP,所以DM 平面MNP,又DM 平面ABMD,所以AB∥DM.又由AD平行且等于BC,得四边形ABCD是平行四边形,故AB∥CD.在平面ABCD中过点D有两条相交直线平行于AB,与平行公理矛盾.于是AB与平面MNP不平行.
三、解答题:本大题共5小题,共48分,其中第14小题8分,第15~18小题各10分.解答应写出文字说明、证明过程或演算步骤.
14.四棱锥P-ABCD中,底面ABCD是矩形,PD⊥底面ABCD,AD=PD,E、F分别为CD、PB的中点,求证:EF⊥面PAB.
证明:
如图,连结EP.
∵PD⊥面ABCD,DE在面ABCD内,
∴PD⊥DE,又CE=ED,PD=AD=BC.
∴Rt△BCE≌Rt△PDE.∴PE=BE.
∵F为PB的中点,∴EF⊥PB,
∵PD⊥ABCD
AB ABCD
∴PD⊥AB
又∵AB⊥AD∴AB⊥平面PAD∴PA⊥AB
∴在Rt△PAB中,PF=AF,又PE=BE=EA,
∴△EFP≌△EFA,∴EF⊥FA.
又PB,FA为平面PAB内相交直线
∴EF⊥面PAB.
15.
如图所示,在正三角形ABC中,E、F分别是AB、AC的中点,AD⊥BC,EH⊥BC,FG⊥BC,D、H、G为垂足,若将正△ABC绕AD旋转一周所得圆锥体积为V,求由阴影部分所产生旋转体的体积与V的比值.
解:
如图所示,设圆锥的高为h,底面半径为r,则圆柱的高为,底半径为,则=1-=1-=1-=.
16.如图所示,在侧棱垂直于底面ABC的三棱柱ABC-A1B1C1中,
A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F是B1C1的中点.求证:
(1)平面ADE⊥平面BCC1B1;
(2)直线A1F∥平面ADE.
证明:(1)因为CC1⊥平面ABC,又AD 平面ABC,所以CC1⊥AD.
又因为AD⊥DE,CC1,DE 平面BCC1B1,CC1∩DE=E,所以AD⊥平面BCC1B1.又AD 平面ADE,
所以平面ADE⊥平面BCC1B1.
(2)因为A1B1=A1C1,F为B1C1的中点,所以A1F⊥B1C1.
因为CC1⊥平面A1B1C1,且A1F 平面A1B1C1,所以CC1⊥A1F.
又因为CC1,B1C1 平面BCC1B1,CC1∩B1C1=C1,所以A1F⊥平面BCC1B1.
由(1)知AD⊥平面BCC1B1,所以A1F∥AD.
又AD 平面ADE,A1F 平面ADE,所以A1F∥平面ADE.
17.如图所示,AB是圆柱的母线,O′是上底面的圆心,△BCD是下底面圆的内接三角形,且BD是下底面圆的直径,E是CD的中点.求证:
(1)O′E∥平面ABC;
(2)平面O′CD⊥平面ABC.
解:
(1)取BC中点为F,连结EF,O′A,
则EF是△BCD的中位线,
∴EF綊BD.
设下底面圆心为O,连结OO′,∵AB是母线,
∴AB綊OO′,
∴AO′綊EF,
∴AF∥O′E且AF 平面ABC,O′E 平面ABC,
∴O′E∥平面ABC.
(2)在圆柱中,AB⊥平面BCD,∴AB⊥CD
∵BC⊥CD,AB∩BC=B
∴CD⊥平面ABC
∵CD 平面O′CD
∴平面O′CD⊥平面ABC.
18.如图所示,在侧面均垂直于底面ABC的三棱柱ABC-A′B′C′中,∠BAC=90°,AB=AC=,AA′=1,点M,N分别为A′B和B′C′的中点.
(1)证明:MN∥平面A′ACC′;
(2)求三棱锥A′-MNC的体积.
解:
(1)(法一)连接AB′,AC′,由已知∠BAC=90°,AB=AC,三棱柱ABC-A′B′C′为直三棱柱,所以M为AB′中点.
又因为N为B′C′的中点,
所以MN∥AC′.
又MN 平面A′ACC′,
AC′ 平面A′ACC′,
因此MN∥平面A′ACC′.
(法二)取A′B′中点P,连接MP,NP,
则M,N分别为AB′与B′C′的中点,所以MP∥AA′,PN∥A′C′,
所以MP∥平面A′ACC′,PN∥平面A′ACC′.
又MP∩NP=P,因此平面MPN∥平面A′ACC′.
而MN 平面MPN,因此MN∥平面A′ACC′.
(2)(法一)连接BN,由题意A′N⊥B′C′,平面A′B′C′∩平面B′BCC′=B′C′,
所以A′N⊥平面NBC.
又A′N=B′C′=1,故VA′-MNC=VN-A′MC=VN-A′BC=VA′-NBC=.
(法二)VA′-MNC=VA′-NBC-VM-NBC
=VA′-NBC=.
