九年级数学上册 21.2.4一元二次方程根与系数的关系 课件
文档属性
| 名称 | 九年级数学上册 21.2.4一元二次方程根与系数的关系 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-18 12:47:32 | ||
图片预览








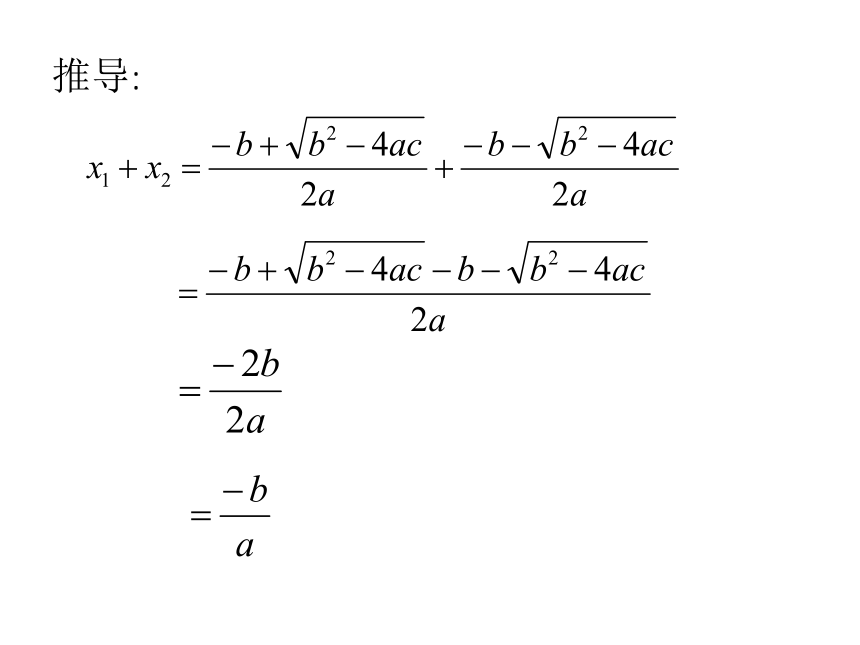
文档简介
课件27张PPT。22.2.4 一元二次方程的根与系数的关系1.一元二次方程的一般形式是什么?3.一元二次方程的根的情况怎样确定?2.一元二次方程的求根公式是什么?4、求一个一元二次方程,使它的两个 根分别为
①2和3;②-4和7;③3和-8;④-5和-2①(x-2)(x-3)=0x2-5x+6=0x2-3x-28=0③(x-3)(x+8)=0 x2+5x-24=0④(x+5)(x+2)=0②(x+4)(x-7)=0x2+7x+10=0问题1:从求这些方程的过程中你发现根
与各项系数之间有什么关系?1.?填表,观察、猜想 问题:你发现什么规律?
①用语言叙述你发现的规律;
② x2+px+q=0的两根x1,, x2用式子表示你发现的规律。 新课讲解如果方程x2+px+q=0有两个根是x1,x2 那么有x1+ x2=-p, x1 ?x2=q猜想:2x2-5x+3=0,这个方程的两根之和,两根之积与各项系数之间有什么关系?问题2;对于一元二次方程的一般式是否也具备这个特征?根与系数关系 如果关于x的方程的两根是 , ,则:如果方程二次项系数不为1呢?问题:上面发现的结论在这里成立吗?请完善规律;
①用语言叙述发现的规律;
② ax2+bx+c=0的两根x1,, x2用式子表示你发现的规
律:
已知:如果一元二次方程
的两个根分别是 、 。求证:推导: 如果一元二次方程
的两个根分别是 、 ,那么:这就是一元二次方程根与系数的关系,也叫韦达定理。1、 x2 - 2x - 1=02、 2x2 - 3x + =03、 2x2 - 6x =04、 3x2 = 4x1+x2=2x1x2=-1x1+x2=x1+x2=3x1+x2=0x1x2=x1x2=0x1x2= -示例一元二次方程的 根与系数的关系 16世纪法国最杰出的数学家韦达发现
代数方程的根与系数之间有这种关系,因此,人们把这个关系称为韦达定理。数学原本只是韦达的业余爱好,但就是这个业余爱好,使他取得了伟大的成就。韦达是第一个有意识地和系统地使用字母表示数的人,并且对数学符号进行了很多改进。是他确定了符号代数的原理与方法,使当时的代数学系统化并且把代数学作为解析的方法使用。因此,他获得了“代数学之父”之称。 1.3.2.4.5.口答下列方程的两根之和与两根之积。例1:根据一元二次方程的根与系数的关系,求下列方程两个根的和与积.的值。解:根据根与系数的关系: 例3: 已知方程 的一个根是2,求它的另一个根及k的值. 解:设方程 的两个根
分别是 、 ,其中 。
所以:
即:
由于
得:k=-7
答:方程的另一个根是 ,k=-7
举一反三:已知方程 的一个根是-3,求它的另一个根及k的值. 已知方程 的两个实数根
是 且 ,求k的值。 解:由根与系数的关系得
X1+X2=-k, X1×X2=k+2
又 X12+ X2 2 = 4
即(X1+ X2)2 -2X1X2=4
K2- 2(k+2)=4
K2-2k-8=0
∵ △= K2-4k-8
当k=4时, △<0
当k=-2时,△>0
∴ k=-2解得:k=4 或k=-2
我要冲关: 2.应用一元二次方程的根与系数关系时,
首先要把已知方程化成一般形式. 3.应用一元二次方程的根与系数关系时,
要特别注意,方程有实根的条件,即在初
中代数里,当且仅当 时,才
能应用根与系数的关系. 1.一元二次方程根与系数的关系是什么?总结归纳巩固练习1:巩固练习2:
5、已知方程 的两根互为相反数,求k的值。
6、已知关于的方程 的一个根是另一个根的2倍,求m的值。
7、已知 的两个实数根,求 的值。挑战自己:8、关于 x的方程 的两实数根之和等于两实数根的倒数和,求m 的值.
9、已知关于X的方程 (1)当方程有两个实数根时,求k的取值范围,的值为整,求整数k的值 。 (2)如果x1、 x2是方程的两个实数根,要使挑战自己:10、方程
有一个正根,一个负根,求m的取值范围。解:由已知,△={即{m>0
m-1<0∴0(1). (2).
(3). (4).
(5). (6).
11:几种常见的变形
与各项系数之间有什么关系?1.?填表,观察、猜想 问题:你发现什么规律?
①用语言叙述你发现的规律;
② x2+px+q=0的两根x1,, x2用式子表示你发现的规律。 新课讲解如果方程x2+px+q=0有两个根是x1,x2 那么有x1+ x2=-p, x1 ?x2=q猜想:2x2-5x+3=0,这个方程的两根之和,两根之积与各项系数之间有什么关系?问题2;对于一元二次方程的一般式是否也具备这个特征?根与系数关系 如果关于x的方程的两根是 , ,则:如果方程二次项系数不为1呢?问题:上面发现的结论在这里成立吗?请完善规律;
①用语言叙述发现的规律;
② ax2+bx+c=0的两根x1,, x2用式子表示你发现的规
律:
已知:如果一元二次方程
的两个根分别是 、 。求证:推导: 如果一元二次方程
的两个根分别是 、 ,那么:这就是一元二次方程根与系数的关系,也叫韦达定理。1、 x2 - 2x - 1=02、 2x2 - 3x + =03、 2x2 - 6x =04、 3x2 = 4x1+x2=2x1x2=-1x1+x2=x1+x2=3x1+x2=0x1x2=x1x2=0x1x2= -示例一元二次方程的 根与系数的关系 16世纪法国最杰出的数学家韦达发现
代数方程的根与系数之间有这种关系,因此,人们把这个关系称为韦达定理。数学原本只是韦达的业余爱好,但就是这个业余爱好,使他取得了伟大的成就。韦达是第一个有意识地和系统地使用字母表示数的人,并且对数学符号进行了很多改进。是他确定了符号代数的原理与方法,使当时的代数学系统化并且把代数学作为解析的方法使用。因此,他获得了“代数学之父”之称。 1.3.2.4.5.口答下列方程的两根之和与两根之积。例1:根据一元二次方程的根与系数的关系,求下列方程两个根的和与积.的值。解:根据根与系数的关系: 例3: 已知方程 的一个根是2,求它的另一个根及k的值. 解:设方程 的两个根
分别是 、 ,其中 。
所以:
即:
由于
得:k=-7
答:方程的另一个根是 ,k=-7
举一反三:已知方程 的一个根是-3,求它的另一个根及k的值. 已知方程 的两个实数根
是 且 ,求k的值。 解:由根与系数的关系得
X1+X2=-k, X1×X2=k+2
又 X12+ X2 2 = 4
即(X1+ X2)2 -2X1X2=4
K2- 2(k+2)=4
K2-2k-8=0
∵ △= K2-4k-8
当k=4时, △<0
当k=-2时,△>0
∴ k=-2解得:k=4 或k=-2
我要冲关: 2.应用一元二次方程的根与系数关系时,
首先要把已知方程化成一般形式. 3.应用一元二次方程的根与系数关系时,
要特别注意,方程有实根的条件,即在初
中代数里,当且仅当 时,才
能应用根与系数的关系. 1.一元二次方程根与系数的关系是什么?总结归纳巩固练习1:巩固练习2:
5、已知方程 的两根互为相反数,求k的值。
6、已知关于的方程 的一个根是另一个根的2倍,求m的值。
7、已知 的两个实数根,求 的值。挑战自己:8、关于 x的方程 的两实数根之和等于两实数根的倒数和,求m 的值.
9、已知关于X的方程 (1)当方程有两个实数根时,求k的取值范围,的值为整,求整数k的值 。 (2)如果x1、 x2是方程的两个实数根,要使挑战自己:10、方程
有一个正根,一个负根,求m的取值范围。解:由已知,△={即{m>0
m-1<0∴0
(3). (4).
(5). (6).
11:几种常见的变形
同课章节目录
