12.3 角的平分线的性质同步练习(解析版)
文档属性
| 名称 | 12.3 角的平分线的性质同步练习(解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 412.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-18 00:00:00 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
新人教版八年级数学上册同步练习
12.3角的平分线的性质
一、单选题
1、已知,Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=32,且BD:CD=9:7,则D到AB的距离为( ) 【版权所有:21教育】
A、18 B、16 C、14 D、12
2、如图,△ABC中,∠C = 90°,AD是∠BAC的平分线,DE⊥AB于E,若DE = 8cm,DB = 10cm则BC等于( )
A、14cm B、16cm C、18cm D、20cm
3、如图,已知点P到AE、AD、BC的距离相等,下列说法:
①点P在∠BAC的平分线上;
②点P在∠CBE的平分线上;
③点P在∠BCD的平分线上;
④点P在∠BAC,∠CBE,∠BCD的平分线的交点上.
其中正确的是( )
www-2-1-cnjy-com
A、①②③④ B、①②③ C、④ D、②③
4、如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于,且OD=4,△ABC的面积是( )21教育网
A、25 B、84 C、42 D、21
5、如图,在 ABCD中,AB=4,AD=7,∠ABC的平分线BE交AD于点E , 则DE的长是( )
A、4 B、3 C、3.5 D、2
6、下列说法正确的是( )
A、角平分线上的点到这个角两边的距离相等
B、角平分线就是角的对称轴
C、如果两个角相等,那么这两个角互为对顶角
D、有一条公共边的两个角互为补角
7、如图,点E是BC的中点,AB⊥BC , DC⊥BC , AE平分∠BAD , 下列结论:
①∠AED=90° ②∠ADE=∠CDE ③DE=BE④AD=AB+CD , 四个结论中成立的是( )
【出处:21教育名师】
A、①②④ B、①②③ C、②③④ D、①③④
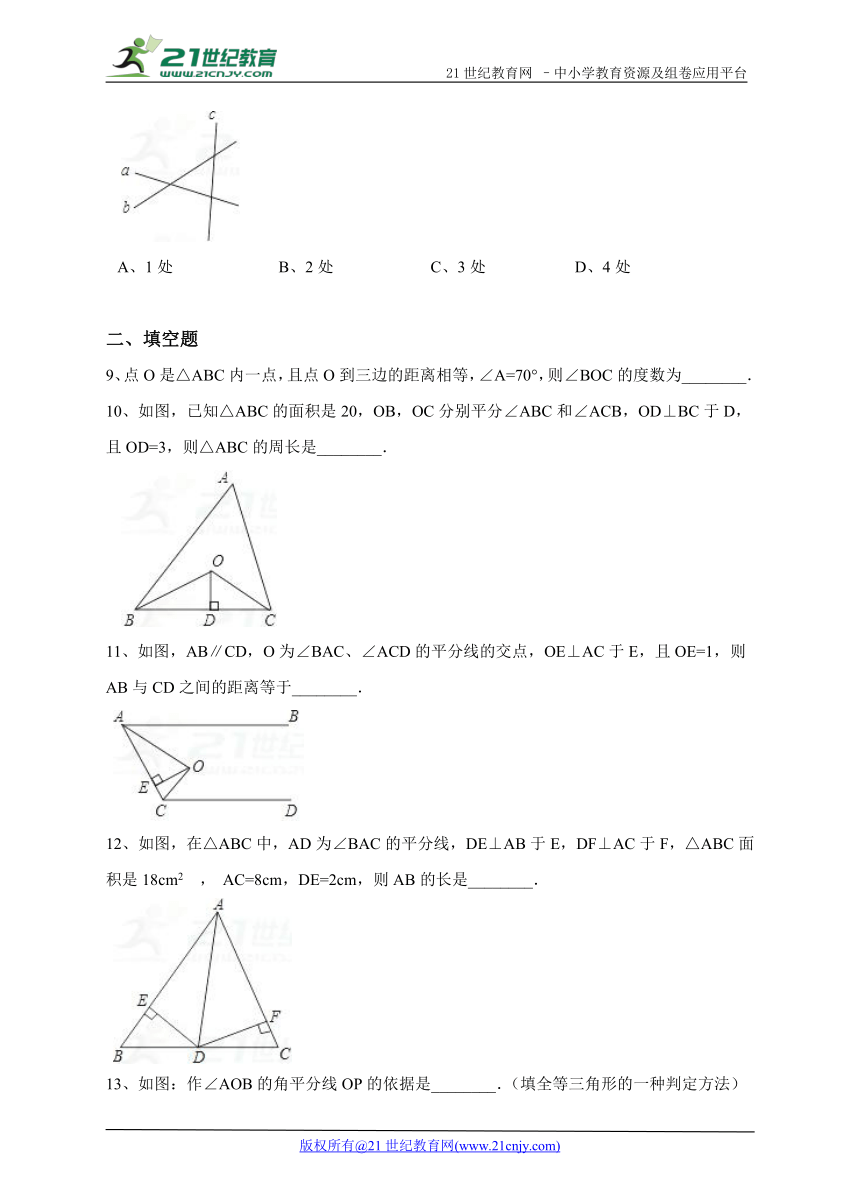
8、如图,直线a、b、c表示三条互相交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
A、1处 B、2处 C、3处 D、4处
二、填空题
9、点O是△ABC内一点,且点O到三边的距离相等,∠A=70°,则∠BOC的度数为________.
10、如图,已知△ABC的面积是20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的周长是________.【来源:21·世纪·教育·网】
11、如图,AB∥CD,O为∠BAC、∠ACD的平分线的交点,OE⊥AC于E,且OE=1,则AB与CD之间的距离等于________. 【来源:21cnj*y.co*m】
12、如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是18cm2 , AC=8cm,DE=2cm,则AB的长是________.
13、如图:作∠AOB的角平分线OP的依据是________.(填全等三角形的一种判定方法)
14、如图,在△ABC中,∠C=90°,AM是∠BAC的平分线,CM=20cm,那么M到AB的距离为________ 21·世纪*教育网
三、解答题
15、已知:如图,AD为∠BAC的平分线,且DF⊥AC于F,∠B=90°,DE=DC.试问BE与CF的关系,并加以说明.21·cn·jy·com
16、已知,如图,在四边形ABCD中,BC>BA,∠A+∠C=180°,DE⊥BC,BD平分∠ABC,试说明AD=DC.
17、如图,已知BE⊥AD,CF⊥AD,且BE=CF.请你判断AD是△ABC的中线还是角平分线?请说明你的理由.
18、如图,小明用三角尺画∠AOB的平分线,他先在∠AOB两边OA,OB上分别取OM=ON,OD=OE,然后,连接DN和EM,相交于点C,再作射线OC,此时他认为OC就是∠AOB的平分线,你认为他的做法正确吗?请说明理由.
参考答案与试题解析
一、单选题
1、C
解:如图,
∵BD+CD=BC=32,BD:DC=9:7
∴CD=14
作DE⊥AB于E,
∵∠C=90°,AD平分∠BAC
∴DE=CD=14.(角平分线上的点到角的两边的距离相等)
即:点D到AB的距离为14,
故选C. 21世纪教育网版权所有
2、C
解:已知△ABC中,∠C = 90°,AD是∠BAC的平分线,DE⊥AB于E,根据角平分线的性质可得CD=DE=8cm,所以BC=CD+BD=18cm,故选C. 2·1·c·n·j·y
3、A
解:∵点P到AE、AD、BC的距离相等, ∴点P在∠BAC的平分线上,故①正确;
点P在∠CBE的平分线上,故②正确;
点P在∠BCD的平分线上,故③正确;
点P在∠BAC,∠CBE,∠BCD的平分线的交点上,故④正确,
综上所述,正确的是①②③④.
故选A. 21*cnjy*com
4、C
解:连接OA,作OE⊥AB于E,OF⊥AC于F,如图, ∵OB,OC分别平分∠ABC和∠ACB,
∴OD=OE=4,OD=OF=4,
∴△ABC的面积=
S△AOB+S△BOC+S△AOC
= OE AB+ OD BC+ OF AC
= ×4×(AB+BC+AC)
= ×4×21
=42.
故选C.
www.21-cn-jy.com
5、B
解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AEB=∠EBC,
又∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE,
∴ED=AD-AE=AD-AB=7-4=3.
故选B. 21*cnjy*com
6、A
解:A.根据角平分线的性质可知,角平分线上的点到这个角两边的距离相等,故A正确;
B根据角的轴对称性质可知,角平分线所在直线就是角的对称轴,故B错误;
C根据对顶角的定义可知,如果一个角的两边分别是另一个角两边的反向延长线,且这两个角有公共顶点,那么这两个角互为对顶角,故C错误;
D根据补角的定义可知,如果两个角的和为180 ,那么这两个角互为补角,故D错误。
故选:A
7、A
解:
如图,过E作EF⊥AD于F.
∵AB⊥BC , AE平分∠BAD ,
∴Rt△AEF≌Rt△AEB ,
∴BE=EF , AB=AF , ∠AEF=∠AEB;
而点E是BC的中点,
∴EC=EF=BE , 所以③错误;
∵Rt△EFD≌Rt△ECD ,
∴DC=DF , ∠FDE=∠CDE , 所以②正确;
∵AD=AF+FD=AB+DC , 所以④正确;
.
故选A.
8、D
解:∵△ABC内角平分线的交点到三角形三边的距离相等, ∴△ABC内角平分线的交点满足条件;
如图:点P是△ABC两条外角平分线的交点,
过点P作PE⊥AB,PD⊥BC,PF⊥AC,
∴PE=PF,PF=PD,
∴PE=PF=PD,
∴点P到△ABC的三边的距离相等,
∴△ABC两条外角平分线的交点到其三边的距离也相等,满足这条件的点有3个;
综上,到三条公路的距离相等的点有4个,
∴可供选择的地址有4个.
故选D.
二、填空题
9、125°
解:连接OA,OB,OC, ∵点O是△ABC内一点,且点O到三边的距离相等,
∴OA、OB、OC分别平分∠BAC、∠ABC、∠ACB,
∵∠BAC=70°,∴∠ABC+∠ACB=110°,
∴∠OBC+∠OCB=110°÷2=55°,
∴∠BOC=180°﹣55°=125°.
故答案为:125°.
10、
解:如图,连接OA, ∵OB、OC分别平分∠ABC和∠ACB,
∴点O到AB、AC、BC的距离都相等,
∵△ABC的面积是20,OD⊥BC于D,且OD=3,
∴S△ABC=×(AB+BC+AC)×3=20.
∴AB+BC+AC=,
故答案为:.
11、2
解:过O作OF⊥AB,OG⊥CD, ∵AO为∠BAC的平分线,且OE⊥AC,OF⊥AB,
∴OE=OF=1,
∵CO为∠BAC的平分线,且OE⊥AC,OG⊥CD,
∴OG=OE=1,
∴FG=OF+OG=2,
∵AB∥CD,
∴AB与CD之间的距离等于2,
故答案为:2
21cnjy.com
12、10cm
解:∵AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,DE=2cm, ∴DF=DE=2cm,
∵△ABC面积是18cm2 ,
∴S△ABD+S△ACD=S△ABC=18cm2 ,
∵AC=8cm,DE=DF=2cm,
∴ AB×2+ ×8×2=18,
∴AB=10(cm),
故答案为:10cm.
13、SSS
解:在△OPC与△OPD中,
∵ ,
∴△OPC≌△OPD(SSS),
∴OP是∠AOB的平分线.
故答案为:SSS.
14、20cm
解:如图,过点M作DM⊥AB于D,
∵∠C=90°,AM是∠CAB的平分线,
∴DM=CM=20cm,
即M到AB的距离为20cm.
故答案为:20cm.
2-1-c-n-j-y
三、解答题
15、解:BE=CF. 理由:∵∠B=90°,
∴BD⊥AB.
∵AD为∠BAC的平分线,且DF⊥AC,
∴DB=DF.
在Rt△BDE和Rt△FDC中,
,
∴Rt△BDE≌Rt△FDC(HL),
∴BE=CF
16、证明:
如图,过D作DF⊥AB,交BA的延长线于点F,
∵DE⊥BC,BD平分∠ABC,
∴DE=DF,∠F=∠DEC=90°,
∵∠BAD+∠C=180°,且∠BAD+∠DAF=180°,
∴∠DAF=∠C,
在△ADF和△CDE中
∴△ADF≌△CDE(AAS),
∴AD=CD
17、解:AD是△ABC的中线.理由如下: ∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD=90°,
在△BDE和△CDF中,21教育名师原创作品
∴△BDE≌△CDF(AAS),
∴BD=CD.
∴AD是△ABC的中线.
18、解:他的做法正确; 理由:在△MOE和△NOD中
,
∴△MOE≌△NOD(SAS),
∴∠OME=∠DNO,
∵OM=ON,OD=OE,
∴DM=EN,
∴在△MDC和△NEC中
,
∴△MDC≌△NEC(AAS),
∴DC=EC,
在△DOC和△EOC中
,
∴△DOC≌△EOC(SSS),
∴∠DOC=∠EOC,
∴OC就是∠AOB的平分线.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
新人教版八年级数学上册同步练习
12.3角的平分线的性质
一、单选题
1、已知,Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=32,且BD:CD=9:7,则D到AB的距离为( ) 【版权所有:21教育】
A、18 B、16 C、14 D、12
2、如图,△ABC中,∠C = 90°,AD是∠BAC的平分线,DE⊥AB于E,若DE = 8cm,DB = 10cm则BC等于( )
A、14cm B、16cm C、18cm D、20cm
3、如图,已知点P到AE、AD、BC的距离相等,下列说法:
①点P在∠BAC的平分线上;
②点P在∠CBE的平分线上;
③点P在∠BCD的平分线上;
④点P在∠BAC,∠CBE,∠BCD的平分线的交点上.
其中正确的是( )
www-2-1-cnjy-com
A、①②③④ B、①②③ C、④ D、②③
4、如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于,且OD=4,△ABC的面积是( )21教育网
A、25 B、84 C、42 D、21
5、如图,在 ABCD中,AB=4,AD=7,∠ABC的平分线BE交AD于点E , 则DE的长是( )
A、4 B、3 C、3.5 D、2
6、下列说法正确的是( )
A、角平分线上的点到这个角两边的距离相等
B、角平分线就是角的对称轴
C、如果两个角相等,那么这两个角互为对顶角
D、有一条公共边的两个角互为补角
7、如图,点E是BC的中点,AB⊥BC , DC⊥BC , AE平分∠BAD , 下列结论:
①∠AED=90° ②∠ADE=∠CDE ③DE=BE④AD=AB+CD , 四个结论中成立的是( )
【出处:21教育名师】
A、①②④ B、①②③ C、②③④ D、①③④
8、如图,直线a、b、c表示三条互相交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
A、1处 B、2处 C、3处 D、4处
二、填空题
9、点O是△ABC内一点,且点O到三边的距离相等,∠A=70°,则∠BOC的度数为________.
10、如图,已知△ABC的面积是20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的周长是________.【来源:21·世纪·教育·网】
11、如图,AB∥CD,O为∠BAC、∠ACD的平分线的交点,OE⊥AC于E,且OE=1,则AB与CD之间的距离等于________. 【来源:21cnj*y.co*m】
12、如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是18cm2 , AC=8cm,DE=2cm,则AB的长是________.
13、如图:作∠AOB的角平分线OP的依据是________.(填全等三角形的一种判定方法)
14、如图,在△ABC中,∠C=90°,AM是∠BAC的平分线,CM=20cm,那么M到AB的距离为________ 21·世纪*教育网
三、解答题
15、已知:如图,AD为∠BAC的平分线,且DF⊥AC于F,∠B=90°,DE=DC.试问BE与CF的关系,并加以说明.21·cn·jy·com
16、已知,如图,在四边形ABCD中,BC>BA,∠A+∠C=180°,DE⊥BC,BD平分∠ABC,试说明AD=DC.
17、如图,已知BE⊥AD,CF⊥AD,且BE=CF.请你判断AD是△ABC的中线还是角平分线?请说明你的理由.
18、如图,小明用三角尺画∠AOB的平分线,他先在∠AOB两边OA,OB上分别取OM=ON,OD=OE,然后,连接DN和EM,相交于点C,再作射线OC,此时他认为OC就是∠AOB的平分线,你认为他的做法正确吗?请说明理由.
参考答案与试题解析
一、单选题
1、C
解:如图,
∵BD+CD=BC=32,BD:DC=9:7
∴CD=14
作DE⊥AB于E,
∵∠C=90°,AD平分∠BAC
∴DE=CD=14.(角平分线上的点到角的两边的距离相等)
即:点D到AB的距离为14,
故选C. 21世纪教育网版权所有
2、C
解:已知△ABC中,∠C = 90°,AD是∠BAC的平分线,DE⊥AB于E,根据角平分线的性质可得CD=DE=8cm,所以BC=CD+BD=18cm,故选C. 2·1·c·n·j·y
3、A
解:∵点P到AE、AD、BC的距离相等, ∴点P在∠BAC的平分线上,故①正确;
点P在∠CBE的平分线上,故②正确;
点P在∠BCD的平分线上,故③正确;
点P在∠BAC,∠CBE,∠BCD的平分线的交点上,故④正确,
综上所述,正确的是①②③④.
故选A. 21*cnjy*com
4、C
解:连接OA,作OE⊥AB于E,OF⊥AC于F,如图, ∵OB,OC分别平分∠ABC和∠ACB,
∴OD=OE=4,OD=OF=4,
∴△ABC的面积=
S△AOB+S△BOC+S△AOC
= OE AB+ OD BC+ OF AC
= ×4×(AB+BC+AC)
= ×4×21
=42.
故选C.
www.21-cn-jy.com
5、B
解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AEB=∠EBC,
又∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE,
∴ED=AD-AE=AD-AB=7-4=3.
故选B. 21*cnjy*com
6、A
解:A.根据角平分线的性质可知,角平分线上的点到这个角两边的距离相等,故A正确;
B根据角的轴对称性质可知,角平分线所在直线就是角的对称轴,故B错误;
C根据对顶角的定义可知,如果一个角的两边分别是另一个角两边的反向延长线,且这两个角有公共顶点,那么这两个角互为对顶角,故C错误;
D根据补角的定义可知,如果两个角的和为180 ,那么这两个角互为补角,故D错误。
故选:A
7、A
解:
如图,过E作EF⊥AD于F.
∵AB⊥BC , AE平分∠BAD ,
∴Rt△AEF≌Rt△AEB ,
∴BE=EF , AB=AF , ∠AEF=∠AEB;
而点E是BC的中点,
∴EC=EF=BE , 所以③错误;
∵Rt△EFD≌Rt△ECD ,
∴DC=DF , ∠FDE=∠CDE , 所以②正确;
∵AD=AF+FD=AB+DC , 所以④正确;
.
故选A.
8、D
解:∵△ABC内角平分线的交点到三角形三边的距离相等, ∴△ABC内角平分线的交点满足条件;
如图:点P是△ABC两条外角平分线的交点,
过点P作PE⊥AB,PD⊥BC,PF⊥AC,
∴PE=PF,PF=PD,
∴PE=PF=PD,
∴点P到△ABC的三边的距离相等,
∴△ABC两条外角平分线的交点到其三边的距离也相等,满足这条件的点有3个;
综上,到三条公路的距离相等的点有4个,
∴可供选择的地址有4个.
故选D.
二、填空题
9、125°
解:连接OA,OB,OC, ∵点O是△ABC内一点,且点O到三边的距离相等,
∴OA、OB、OC分别平分∠BAC、∠ABC、∠ACB,
∵∠BAC=70°,∴∠ABC+∠ACB=110°,
∴∠OBC+∠OCB=110°÷2=55°,
∴∠BOC=180°﹣55°=125°.
故答案为:125°.
10、
解:如图,连接OA, ∵OB、OC分别平分∠ABC和∠ACB,
∴点O到AB、AC、BC的距离都相等,
∵△ABC的面积是20,OD⊥BC于D,且OD=3,
∴S△ABC=×(AB+BC+AC)×3=20.
∴AB+BC+AC=,
故答案为:.
11、2
解:过O作OF⊥AB,OG⊥CD, ∵AO为∠BAC的平分线,且OE⊥AC,OF⊥AB,
∴OE=OF=1,
∵CO为∠BAC的平分线,且OE⊥AC,OG⊥CD,
∴OG=OE=1,
∴FG=OF+OG=2,
∵AB∥CD,
∴AB与CD之间的距离等于2,
故答案为:2
21cnjy.com
12、10cm
解:∵AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,DE=2cm, ∴DF=DE=2cm,
∵△ABC面积是18cm2 ,
∴S△ABD+S△ACD=S△ABC=18cm2 ,
∵AC=8cm,DE=DF=2cm,
∴ AB×2+ ×8×2=18,
∴AB=10(cm),
故答案为:10cm.
13、SSS
解:在△OPC与△OPD中,
∵ ,
∴△OPC≌△OPD(SSS),
∴OP是∠AOB的平分线.
故答案为:SSS.
14、20cm
解:如图,过点M作DM⊥AB于D,
∵∠C=90°,AM是∠CAB的平分线,
∴DM=CM=20cm,
即M到AB的距离为20cm.
故答案为:20cm.
2-1-c-n-j-y
三、解答题
15、解:BE=CF. 理由:∵∠B=90°,
∴BD⊥AB.
∵AD为∠BAC的平分线,且DF⊥AC,
∴DB=DF.
在Rt△BDE和Rt△FDC中,
,
∴Rt△BDE≌Rt△FDC(HL),
∴BE=CF
16、证明:
如图,过D作DF⊥AB,交BA的延长线于点F,
∵DE⊥BC,BD平分∠ABC,
∴DE=DF,∠F=∠DEC=90°,
∵∠BAD+∠C=180°,且∠BAD+∠DAF=180°,
∴∠DAF=∠C,
在△ADF和△CDE中
∴△ADF≌△CDE(AAS),
∴AD=CD
17、解:AD是△ABC的中线.理由如下: ∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD=90°,
在△BDE和△CDF中,21教育名师原创作品
∴△BDE≌△CDF(AAS),
∴BD=CD.
∴AD是△ABC的中线.
18、解:他的做法正确; 理由:在△MOE和△NOD中
,
∴△MOE≌△NOD(SAS),
∴∠OME=∠DNO,
∵OM=ON,OD=OE,
∴DM=EN,
∴在△MDC和△NEC中
,
∴△MDC≌△NEC(AAS),
∴DC=EC,
在△DOC和△EOC中
,
∴△DOC≌△EOC(SSS),
∴∠DOC=∠EOC,
∴OC就是∠AOB的平分线.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
