第二十九章 直线与圆的位置关系 达标检测卷(含答案)
文档属性
| 名称 | 第二十九章 直线与圆的位置关系 达标检测卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 348.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-20 08:19:16 | ||
图片预览

文档简介
第二十九章达标检测卷
(120分,90分钟)
题 号
一
二
三
总 分
得 分
一、选择题(每题3分,共48分)
1.已知⊙O的半径为5,点P到圆心O的距离为6,那么点P与⊙O的位置关系是( )
A.点P在⊙O外
B.点P在⊙O内
C.点P在⊙O上
D.无法确定
2.⊙O的直径是3,直线l与⊙O相交,圆心O到直线l的距离是d,则d应满足( )
A.d>3
B.1.5C.0≤d<1.5
D.d>0
3.下列直线中,能判定为圆的切线的是( )
A.与圆有公共点的直线
B.垂直于半径的直线
C.经过半径的外端的直线
D.经过半径的外端并且垂直于这条半径的直线
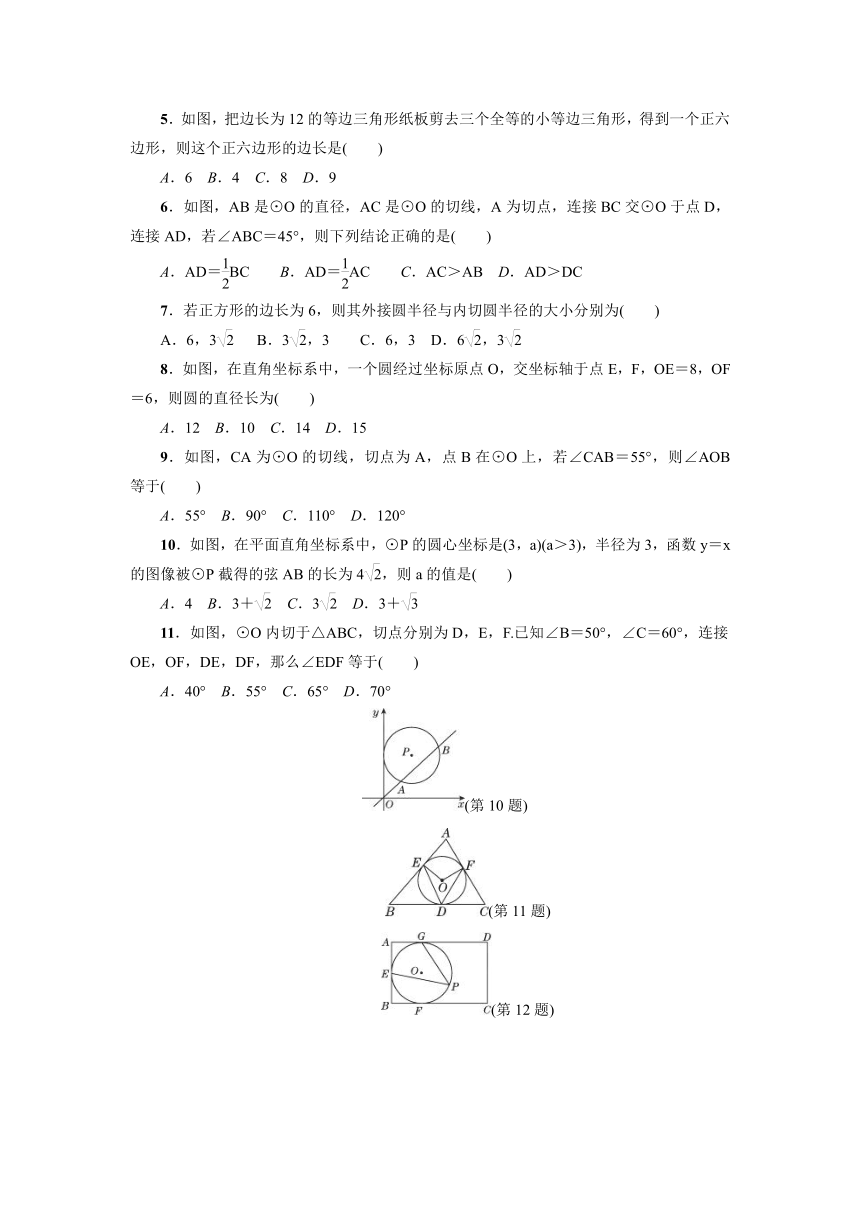
4.如图,⊙O的弦AB=8,M是AB的中点,且OM=3,则⊙O的半径等于( )
A.4
B.5
C.8
D.10
(第4题)
(第5题)
(第6题)
(第8题)
(第9题)
5.如图,把边长为12的等边三角形纸板剪去三个全等的小等边三角形,得到一个正六边形,则这个正六边形的边长是( )
A.6
B.4
C.8
D.9
6.如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,连接BC交⊙O于点D,连接AD,若∠ABC=45°,则下列结论正确的是( )
A.AD=BC
B.AD=AC
C.AC>AB
D.AD>DC
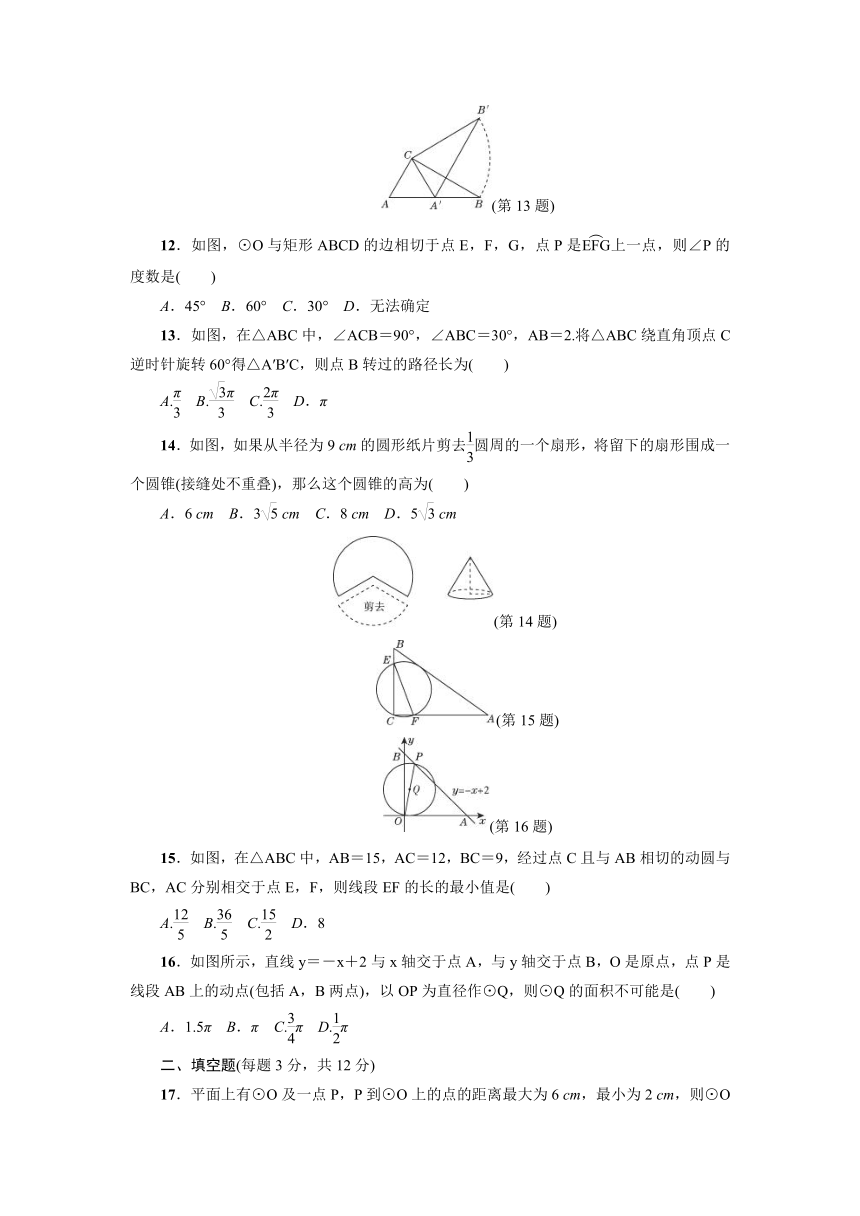
7.若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为( )
A.6,3
B.3,3
C.6,3
D.6,3
8.如图,在直角坐标系中,一个圆经过坐标原点O,交坐标轴于点E,F,OE=8,OF=6,则圆的直径长为( )
A.12
B.10
C.14
D.15
9.如图,CA为⊙O的切线,切点为A,点B在⊙O上,若∠CAB=55°,则∠AOB等于( )
A.55°
B.90°
C.110°
D.120°
10.如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图像被⊙P截得的弦AB的长为4,则a的值是( )
A.4
B.3+
C.3
D.3+
11.如图,⊙O内切于△ABC,切点分别为D,E,F.已知∠B=50°,∠C=60°,连接OE,OF,DE,DF,那么∠EDF等于( )
A.40°
B.55°
C.65°
D.70°
(第10题)
(第11题)
(第12题)
(第13题)
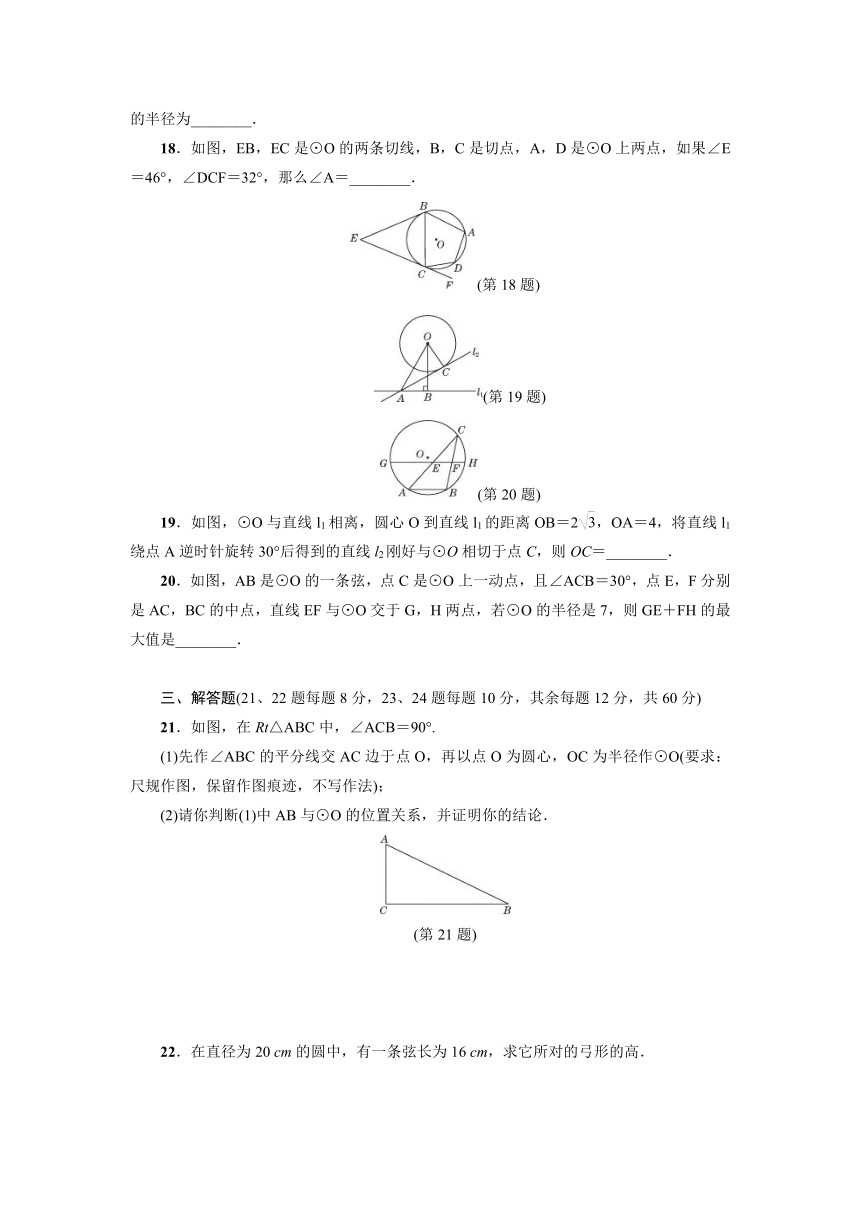
12.如图,⊙O与矩形ABCD的边相切于点E,F,G,点P是上一点,则∠P的度数是( )
A.45°
B.60°
C.30°
D.无法确定
13.如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C,则点B转过的路径长为( )
A.
B.
C.
D.π
14.如图,如果从半径为9
cm的圆形纸片剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为( )
A.6
cm
B.3
cm
C.8
cm
D.5
cm
(第14题)
(第15题)
(第16题)
15.如图,在△ABC中,AB=15,AC=12,BC=9,经过点C且与AB相切的动圆与BC,AC分别相交于点E,F,则线段EF的长的最小值是( )
A.
B.
C.
D.8
16.如图所示,直线y=-x+2与x轴交于点A,与y轴交于点B,O是原点,点P是线段AB上的动点(包括A,B两点),以OP为直径作⊙Q,则⊙Q的面积不可能是( )
A.1.5π
B.π
C.π
D.π
二、填空题(每题3分,共12分)
17.平面上有⊙O及一点P,P到⊙O上的点的距离最大为6
cm,最小为2
cm,则⊙O的半径为________.
18.如图,EB,EC是⊙O的两条切线,B,C是切点,A,D是⊙O上两点,如果∠E=46°,∠DCF=32°,那么∠A=________.
(第18题)
(第19题)
(第20题)
19.如图,⊙O与直线l1相离,圆心O到直线l1的距离OB=2,OA=4,将直线l1绕点A逆时针旋转30°后得到的直线l2刚好与⊙O相切于点C,则OC=________.
20.如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E,F分别是AC,BC的中点,直线EF与⊙O交于G,H两点,若⊙O的半径是7,则GE+FH的最大值是________.
三、解答题(21、22题每题8分,23、24题每题10分,其余每题12分,共60分)
21.如图,在Rt△ABC中,∠ACB=90°.
(1)先作∠ABC的平分线交AC边于点O,再以点O为圆心,OC为半径作⊙O(要求:尺规作图,保留作图痕迹,不写作法);
(2)请你判断(1)中AB与⊙O的位置关系,并证明你的结论.
(第21题)
22.在直径为20
cm的圆中,有一条弦长为16
cm,求它所对的弓形的高.
23.如图,有一个圆O和两个正六边形T1,T2,T1的六个顶点都在圆周上,T2的六条边都和圆O相切(称T1,T2分别为圆O的内接正六边形和外切正六边形).
(1)设T1,T2的边长分别为a,b,圆O的半径为r,求r?a与r?b;
(2)设正六边形T1的面积为S1,T2的面积为S2,求S1?S2.
(第23题)
24.已知:如图,AB为⊙O的直径,点C,D在⊙O上,且BC=6
cm,AC=8
cm,∠ABD=45°.
(1)求BD的长;
(2)求图中阴影部分的面积.
(第24题)
25.如图,点P在y轴上,⊙P交x轴于A,B两点,连接BP并延长交⊙P于点C,过点C的直线y=2x+b交x轴于点D,且⊙P的半径为,AB=4.
(1)求点B,P,C的坐标;
(2)求证:CD是⊙P的切线.
(第25题)
26.如图,已知在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.
(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG·AB=12,求AC的长;
(3)在满足(2)的条件下,若AF∶FD=1∶2,GF=1,求⊙O的半径及sin∠ACE的值.
(第26题)
答案
一、1.A 2.C 3.D 4.B 5.B
6.A 点拨:由AB是⊙O的直径,AC是⊙O的切线,A为切点,可知AD⊥BC,∠BAC=90°.又∵∠ABC=45°,∴∠C=45°,∴AB=AC.根据等腰三角形三线合一的性质可得,D是BC的中点.由直角三角形的性质可知,AD=BC=DC.在Rt△ACD中,∠C=45°,∴AD=AC.
7.B
点拨:因为正方形内切圆半径为正方形边长的一半且正方形边长为6,所以其内切圆半径为3;又因为正方形边长是其外接圆半径的倍,所以其外接圆半径为=3,故选B.
8.B 9.C 10.B
11.B 点拨:由∠B=50°,∠C=60°可求出∠A=70°,则易求得∠EOF=110°,∴∠EDF=∠EOF=55°.
12.A
13.B
14.B 点拨:∵留下的扇形的弧长为×2π×9=12π(cm).∴围成圆锥的底面圆半径r==6(cm).
又∵圆锥母线长l=9
cm,∴h===3(cm).
15.B 点拨:在△ABC中,∵AB=15,AC=12,BC=9,∴AB2=225,AC2+BC2=144+81=225,∴AC2+BC2=AB2,
∴△ABC为直角三角形,且∠C=90°.∴EF是动圆的直径.设AB切动圆于点D,连接CD,当CD垂直于AB,即CD是动圆的直径时,EF的长最小,最小值是=.
16.A 点拨:∵直线y=-x+2与x轴交于点A,与y轴交于点B,
∴OA=OB=2,由勾股定理得AB=2.过O作OC⊥AB于C,则·OB·OA=·AB·OC,解得OC=.当点P,C重合时,⊙Q的面积最小,为π×=π;当点P和A或B重合时,⊙Q的面积最大,为π×12=π.故π≤⊙Q的面积≤π.
二、17.4
cm或2
cm 点拨:本题采用分类讨论思想.点P可能位于⊙O的内部,也可能位于⊙O的外部.
18.99° 点拨:易知EB=EC.又∠E=46°,所以∠ECB=67°.从而∠BCD=180°-67°-32°=81°.在⊙O中,∠BCD与∠A互补,所以∠A=180°-81°=99°.
19.2 点拨:∵OB⊥AB,OB=2,OA=4,∴在Rt△ABO中,sin∠OAB==,则∠OAB=60°.又∵∠CAB=30°,∴∠OAC=∠OAB-∠CAB=30°.∵直线l2刚好与⊙O相切于点C,∴∠ACO=90°,∴在Rt△AOC中,OC=OA=2.
20.10.5
三、21.解:(1)如图所示.
(第21题)
(2)AB与⊙O相切.
证明:作OD⊥AB于点D,如图所示.
∵BO平分∠ABC,∠ACB=90°,
OD⊥AB,
∴OD=OC.∴AB与⊙O相切.
点拨:在证明圆的切线时,如果没有明确直线与圆的公共点,一般过圆心作直线的垂线段,证明圆心到直线的距离等于圆的半径,根据直线与圆的位置关系的判定方法得到圆的切线.
22.解:∵这条小于直径的弦所对的弧有两条:劣弧与优弧,∴对应的弓形也有两个.
如图,HG为⊙O的直径,
且HG⊥AB,AB=16
cm,
HG=20
cm,连接BO.
∴OB=OH=10
cm,BC=AB=8
cm.
∴OC===6(cm).
∴CH=OH-OC=10-6=4(cm),
CG=OC+OG=6+10=16(cm).
故所求弓形的高为4
cm或16
cm.
(第22题)
23.解:(1)∵正六边形的中心角是60°,
∴分别连接圆心O和T1的6个顶点,可得6个全等的等边三角形,即r?a=1?1;
分别连接圆心O和T2的两个相邻顶点,得以圆O的半径为高的正三角形,则b=2×r·tan30°=r,
∴r?b=?2.
(2)由(1)得:a=r,b=r
,
∴S1=6×r·r=r2,S2=6××r·r=2r2,
∴S1?S2=r2?2r2=3?4.
24.解:(1)∵AB为⊙O的直径,
∴∠ACB=90°.
∵BC=6
cm,AC=8
cm,∴AB=10
cm,∴OB=5
cm.
连接OD,∵OD=OB,∴∠ODB=∠ABD=45°.∴∠BOD=90°.∴BD==5
cm.
(2)S阴影=π×52-×5×5=
(cm2).
25.(1)解:如图,连接CA.
∵OP⊥AB,∴OB=OA=2.
∵OP2+BO2=BP2,
∴OP2=5-4=1,OP=1.
∵BC是⊙P的直径,
∴∠CAB=90°.
∵CP=BP,OB=OA,
∴AC=2OP=2.
∴B(2,0),P(0,1),C(-2,2).
(第25题)
(2)证明:∵y=2x+b过C点,
∴b=6.∴y=2x+6.
∵当y=0时,x=-3,
∴D(-3,0).∴AD=1.
∵OB=AC=2,AD=OP=1,
∠CAD=∠POB=90°,
∴△DAC≌△POB.
∴∠DCA=∠ABC.
又∵∠ACB+∠CBA=90°,
∴∠DCA+∠ACB=90°,即CD⊥BC.
∴CD是⊙P的切线.
26.(1)证明:如图,连接CD,
∵AD是⊙O的直径.∴∠ACD=90°.
∴∠CAD+∠ADC=90°.
又∵∠PAC=∠PBA,∠ADC=∠PBA,
∴∠PAC=∠ADC.
∴∠CAD+∠PAC=90°.
∴PA⊥OA.而AD是⊙O的直径,
∴PA是⊙O的切线.
(2)解:由(1)知,PA⊥AD,
又∵CF⊥AD,
∴CF∥PA.∴∠GCA=∠PAC.
又∵∠PAC=∠PBA,
∴∠GCA=∠PBA.
而∠CAG=∠BAC,
∴△CAG∽△BAC.
∴=,
即AC2=AG·AB.
∵AG·AB=12,
∴AC2=12.∴AC=2.
(3)解:设AF=x,∵AF?FD=1?2,
∴FD=2x.∴AD=AF+FD=3x.
在Rt△ACD中,∵CF⊥AD,
∴AC2=AF·AD,即12=3x2,
解得x=2或x=-2(舍去).
∴AF=2,AD=6.∴⊙O的半径为3.
在Rt△AFG中,AF=2,GF=1,
根据勾股定理得AG===,由(2)知AG·AB=12,
∴AB==.连接BD,如图.
∵AD是⊙O的直径,∴∠ABD=90°.
在Rt△ABD中,∵sin∠ADB=,
AD=6,AB=,∴sin∠ADB=.
∵∠ACE=∠ADB,∴sin∠ACE=.
(第26题)
(120分,90分钟)
题 号
一
二
三
总 分
得 分
一、选择题(每题3分,共48分)
1.已知⊙O的半径为5,点P到圆心O的距离为6,那么点P与⊙O的位置关系是( )
A.点P在⊙O外
B.点P在⊙O内
C.点P在⊙O上
D.无法确定
2.⊙O的直径是3,直线l与⊙O相交,圆心O到直线l的距离是d,则d应满足( )
A.d>3
B.1.5
D.d>0
3.下列直线中,能判定为圆的切线的是( )
A.与圆有公共点的直线
B.垂直于半径的直线
C.经过半径的外端的直线
D.经过半径的外端并且垂直于这条半径的直线
4.如图,⊙O的弦AB=8,M是AB的中点,且OM=3,则⊙O的半径等于( )
A.4
B.5
C.8
D.10
(第4题)
(第5题)
(第6题)
(第8题)
(第9题)
5.如图,把边长为12的等边三角形纸板剪去三个全等的小等边三角形,得到一个正六边形,则这个正六边形的边长是( )
A.6
B.4
C.8
D.9
6.如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,连接BC交⊙O于点D,连接AD,若∠ABC=45°,则下列结论正确的是( )
A.AD=BC
B.AD=AC
C.AC>AB
D.AD>DC
7.若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为( )
A.6,3
B.3,3
C.6,3
D.6,3
8.如图,在直角坐标系中,一个圆经过坐标原点O,交坐标轴于点E,F,OE=8,OF=6,则圆的直径长为( )
A.12
B.10
C.14
D.15
9.如图,CA为⊙O的切线,切点为A,点B在⊙O上,若∠CAB=55°,则∠AOB等于( )
A.55°
B.90°
C.110°
D.120°
10.如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图像被⊙P截得的弦AB的长为4,则a的值是( )
A.4
B.3+
C.3
D.3+
11.如图,⊙O内切于△ABC,切点分别为D,E,F.已知∠B=50°,∠C=60°,连接OE,OF,DE,DF,那么∠EDF等于( )
A.40°
B.55°
C.65°
D.70°
(第10题)
(第11题)
(第12题)
(第13题)
12.如图,⊙O与矩形ABCD的边相切于点E,F,G,点P是上一点,则∠P的度数是( )
A.45°
B.60°
C.30°
D.无法确定
13.如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C,则点B转过的路径长为( )
A.
B.
C.
D.π
14.如图,如果从半径为9
cm的圆形纸片剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为( )
A.6
cm
B.3
cm
C.8
cm
D.5
cm
(第14题)
(第15题)
(第16题)
15.如图,在△ABC中,AB=15,AC=12,BC=9,经过点C且与AB相切的动圆与BC,AC分别相交于点E,F,则线段EF的长的最小值是( )
A.
B.
C.
D.8
16.如图所示,直线y=-x+2与x轴交于点A,与y轴交于点B,O是原点,点P是线段AB上的动点(包括A,B两点),以OP为直径作⊙Q,则⊙Q的面积不可能是( )
A.1.5π
B.π
C.π
D.π
二、填空题(每题3分,共12分)
17.平面上有⊙O及一点P,P到⊙O上的点的距离最大为6
cm,最小为2
cm,则⊙O的半径为________.
18.如图,EB,EC是⊙O的两条切线,B,C是切点,A,D是⊙O上两点,如果∠E=46°,∠DCF=32°,那么∠A=________.
(第18题)
(第19题)
(第20题)
19.如图,⊙O与直线l1相离,圆心O到直线l1的距离OB=2,OA=4,将直线l1绕点A逆时针旋转30°后得到的直线l2刚好与⊙O相切于点C,则OC=________.
20.如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E,F分别是AC,BC的中点,直线EF与⊙O交于G,H两点,若⊙O的半径是7,则GE+FH的最大值是________.
三、解答题(21、22题每题8分,23、24题每题10分,其余每题12分,共60分)
21.如图,在Rt△ABC中,∠ACB=90°.
(1)先作∠ABC的平分线交AC边于点O,再以点O为圆心,OC为半径作⊙O(要求:尺规作图,保留作图痕迹,不写作法);
(2)请你判断(1)中AB与⊙O的位置关系,并证明你的结论.
(第21题)
22.在直径为20
cm的圆中,有一条弦长为16
cm,求它所对的弓形的高.
23.如图,有一个圆O和两个正六边形T1,T2,T1的六个顶点都在圆周上,T2的六条边都和圆O相切(称T1,T2分别为圆O的内接正六边形和外切正六边形).
(1)设T1,T2的边长分别为a,b,圆O的半径为r,求r?a与r?b;
(2)设正六边形T1的面积为S1,T2的面积为S2,求S1?S2.
(第23题)
24.已知:如图,AB为⊙O的直径,点C,D在⊙O上,且BC=6
cm,AC=8
cm,∠ABD=45°.
(1)求BD的长;
(2)求图中阴影部分的面积.
(第24题)
25.如图,点P在y轴上,⊙P交x轴于A,B两点,连接BP并延长交⊙P于点C,过点C的直线y=2x+b交x轴于点D,且⊙P的半径为,AB=4.
(1)求点B,P,C的坐标;
(2)求证:CD是⊙P的切线.
(第25题)
26.如图,已知在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.
(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG·AB=12,求AC的长;
(3)在满足(2)的条件下,若AF∶FD=1∶2,GF=1,求⊙O的半径及sin∠ACE的值.
(第26题)
答案
一、1.A 2.C 3.D 4.B 5.B
6.A 点拨:由AB是⊙O的直径,AC是⊙O的切线,A为切点,可知AD⊥BC,∠BAC=90°.又∵∠ABC=45°,∴∠C=45°,∴AB=AC.根据等腰三角形三线合一的性质可得,D是BC的中点.由直角三角形的性质可知,AD=BC=DC.在Rt△ACD中,∠C=45°,∴AD=AC.
7.B
点拨:因为正方形内切圆半径为正方形边长的一半且正方形边长为6,所以其内切圆半径为3;又因为正方形边长是其外接圆半径的倍,所以其外接圆半径为=3,故选B.
8.B 9.C 10.B
11.B 点拨:由∠B=50°,∠C=60°可求出∠A=70°,则易求得∠EOF=110°,∴∠EDF=∠EOF=55°.
12.A
13.B
14.B 点拨:∵留下的扇形的弧长为×2π×9=12π(cm).∴围成圆锥的底面圆半径r==6(cm).
又∵圆锥母线长l=9
cm,∴h===3(cm).
15.B 点拨:在△ABC中,∵AB=15,AC=12,BC=9,∴AB2=225,AC2+BC2=144+81=225,∴AC2+BC2=AB2,
∴△ABC为直角三角形,且∠C=90°.∴EF是动圆的直径.设AB切动圆于点D,连接CD,当CD垂直于AB,即CD是动圆的直径时,EF的长最小,最小值是=.
16.A 点拨:∵直线y=-x+2与x轴交于点A,与y轴交于点B,
∴OA=OB=2,由勾股定理得AB=2.过O作OC⊥AB于C,则·OB·OA=·AB·OC,解得OC=.当点P,C重合时,⊙Q的面积最小,为π×=π;当点P和A或B重合时,⊙Q的面积最大,为π×12=π.故π≤⊙Q的面积≤π.
二、17.4
cm或2
cm 点拨:本题采用分类讨论思想.点P可能位于⊙O的内部,也可能位于⊙O的外部.
18.99° 点拨:易知EB=EC.又∠E=46°,所以∠ECB=67°.从而∠BCD=180°-67°-32°=81°.在⊙O中,∠BCD与∠A互补,所以∠A=180°-81°=99°.
19.2 点拨:∵OB⊥AB,OB=2,OA=4,∴在Rt△ABO中,sin∠OAB==,则∠OAB=60°.又∵∠CAB=30°,∴∠OAC=∠OAB-∠CAB=30°.∵直线l2刚好与⊙O相切于点C,∴∠ACO=90°,∴在Rt△AOC中,OC=OA=2.
20.10.5
三、21.解:(1)如图所示.
(第21题)
(2)AB与⊙O相切.
证明:作OD⊥AB于点D,如图所示.
∵BO平分∠ABC,∠ACB=90°,
OD⊥AB,
∴OD=OC.∴AB与⊙O相切.
点拨:在证明圆的切线时,如果没有明确直线与圆的公共点,一般过圆心作直线的垂线段,证明圆心到直线的距离等于圆的半径,根据直线与圆的位置关系的判定方法得到圆的切线.
22.解:∵这条小于直径的弦所对的弧有两条:劣弧与优弧,∴对应的弓形也有两个.
如图,HG为⊙O的直径,
且HG⊥AB,AB=16
cm,
HG=20
cm,连接BO.
∴OB=OH=10
cm,BC=AB=8
cm.
∴OC===6(cm).
∴CH=OH-OC=10-6=4(cm),
CG=OC+OG=6+10=16(cm).
故所求弓形的高为4
cm或16
cm.
(第22题)
23.解:(1)∵正六边形的中心角是60°,
∴分别连接圆心O和T1的6个顶点,可得6个全等的等边三角形,即r?a=1?1;
分别连接圆心O和T2的两个相邻顶点,得以圆O的半径为高的正三角形,则b=2×r·tan30°=r,
∴r?b=?2.
(2)由(1)得:a=r,b=r
,
∴S1=6×r·r=r2,S2=6××r·r=2r2,
∴S1?S2=r2?2r2=3?4.
24.解:(1)∵AB为⊙O的直径,
∴∠ACB=90°.
∵BC=6
cm,AC=8
cm,∴AB=10
cm,∴OB=5
cm.
连接OD,∵OD=OB,∴∠ODB=∠ABD=45°.∴∠BOD=90°.∴BD==5
cm.
(2)S阴影=π×52-×5×5=
(cm2).
25.(1)解:如图,连接CA.
∵OP⊥AB,∴OB=OA=2.
∵OP2+BO2=BP2,
∴OP2=5-4=1,OP=1.
∵BC是⊙P的直径,
∴∠CAB=90°.
∵CP=BP,OB=OA,
∴AC=2OP=2.
∴B(2,0),P(0,1),C(-2,2).
(第25题)
(2)证明:∵y=2x+b过C点,
∴b=6.∴y=2x+6.
∵当y=0时,x=-3,
∴D(-3,0).∴AD=1.
∵OB=AC=2,AD=OP=1,
∠CAD=∠POB=90°,
∴△DAC≌△POB.
∴∠DCA=∠ABC.
又∵∠ACB+∠CBA=90°,
∴∠DCA+∠ACB=90°,即CD⊥BC.
∴CD是⊙P的切线.
26.(1)证明:如图,连接CD,
∵AD是⊙O的直径.∴∠ACD=90°.
∴∠CAD+∠ADC=90°.
又∵∠PAC=∠PBA,∠ADC=∠PBA,
∴∠PAC=∠ADC.
∴∠CAD+∠PAC=90°.
∴PA⊥OA.而AD是⊙O的直径,
∴PA是⊙O的切线.
(2)解:由(1)知,PA⊥AD,
又∵CF⊥AD,
∴CF∥PA.∴∠GCA=∠PAC.
又∵∠PAC=∠PBA,
∴∠GCA=∠PBA.
而∠CAG=∠BAC,
∴△CAG∽△BAC.
∴=,
即AC2=AG·AB.
∵AG·AB=12,
∴AC2=12.∴AC=2.
(3)解:设AF=x,∵AF?FD=1?2,
∴FD=2x.∴AD=AF+FD=3x.
在Rt△ACD中,∵CF⊥AD,
∴AC2=AF·AD,即12=3x2,
解得x=2或x=-2(舍去).
∴AF=2,AD=6.∴⊙O的半径为3.
在Rt△AFG中,AF=2,GF=1,
根据勾股定理得AG===,由(2)知AG·AB=12,
∴AB==.连接BD,如图.
∵AD是⊙O的直径,∴∠ABD=90°.
在Rt△ABD中,∵sin∠ADB=,
AD=6,AB=,∴sin∠ADB=.
∵∠ACE=∠ADB,∴sin∠ACE=.
(第26题)
