2017-2018学年九年级下数学期末达标检测卷(含答案)
文档属性
| 名称 | 2017-2018学年九年级下数学期末达标检测卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 408.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-20 08:07:41 | ||
图片预览


文档简介
2017-2018学年九年级下数学期末达标检测卷
(120分,90分钟)
题 号
一
二
三
总 分
得 分
一、选择题(每题3分,共48分)
1.若抛物线y=2xm2-4m-3+(m-5)的顶点在x轴的下方,则( )
A.m=5
B.m=-1
C.m=5或m=-1
D.m=-5
2.
在一个不透明的袋子中装有4个红球和3个黑球,它们除颜色外其他均相同,从中任意摸出一个球,则摸出黑球的概率是( )
A.
B.
C.
D.
3.如图是将正方体切去一个角后形成的几何体,则该几何体的左视图为( )
(第3题)
INCLUDEPICTURE
"../../../YXJ18.tif"
\
MERGEFORMAT
4.如图所示,正方形ABCD的边长为1,E,F,G,H分别为各边上的点(与A,B,C,D不重合),且AE=BF=CG=DH,设小正方形EFGH的面积为S,AE的长为x,则S关于x的函数图像大致是( )
(第4题)
5.一个几何体的三视图如图所示,这个几何体是( )
A.球
B.圆柱
C.圆锥
D.立方体
(第5题)
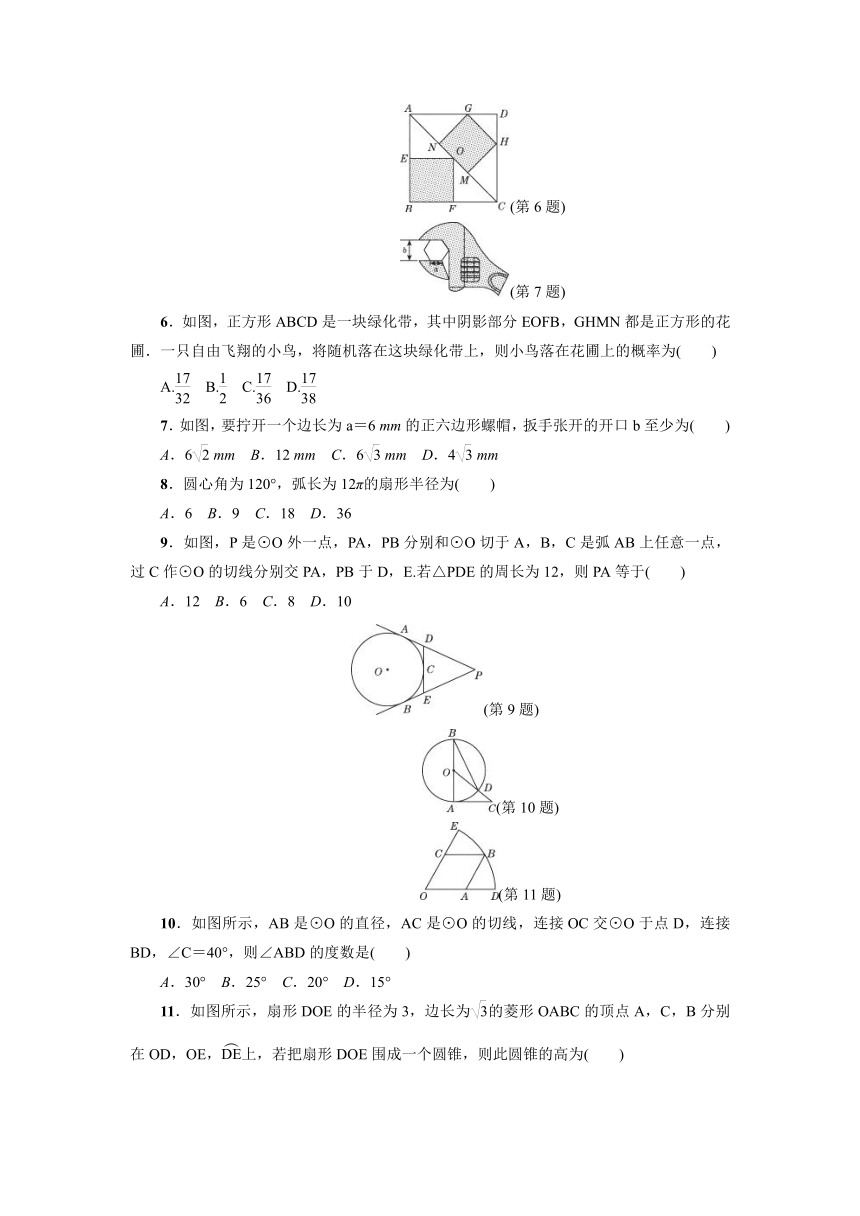
(第6题)
(第7题)
6.如图,正方形ABCD是一块绿化带,其中阴影部分EOFB,GHMN都是正方形的花圃.一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟落在花圃上的概率为( )
A.
B.
C.
D.
7.如图,要拧开一个边长为a=6
mm的正六边形螺帽,扳手张开的开口b至少为( )
A.6
mm
B.12
mm
C.6
mm
D.4
mm
8.圆心角为120°,弧长为12π的扇形半径为( )
A.6
B.9
C.18
D.36
9.如图,P是⊙O外一点,PA,PB分别和⊙O切于A,B,C是弧AB上任意一点,过C作⊙O的切线分别交PA,PB于D,E.若△PDE的周长为12,则PA等于( )
A.12
B.6
C.8
D.10
(第9题)
(第10题)
(第11题)
10.如图所示,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=40°,则∠ABD的度数是( )
A.30°
B.25°
C.20°
D.15°
11.如图所示,扇形DOE的半径为3,边长为的菱形OABC的顶点A,C,B分别在OD,OE,上,若把扇形DOE围成一个圆锥,则此圆锥的高为( )
A.
B.2
C.
D.
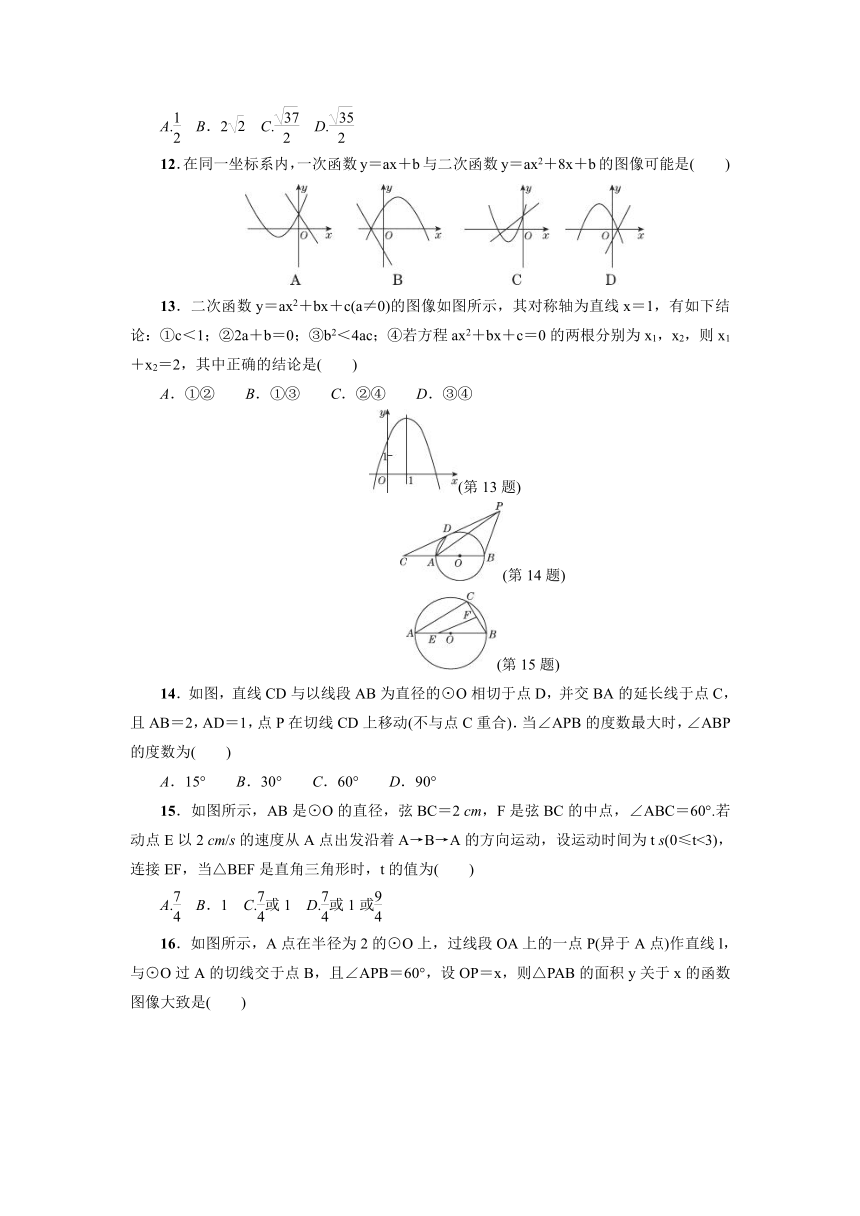
12.在同一坐标系内,一次函数y=ax+b与二次函数y=ax2+8x+b的图像可能是( )
13.二次函数y=ax2+bx+c(a≠0)的图像如图所示,其对称轴为直线x=1,有如下结论:①c<1;②2a+b=0;③b2<4ac;④若方程ax2+bx+c=0的两根分别为x1,x2,则x1+x2=2,其中正确的结论是( )
A.①②
B.①③
C.②④
D.③④
(第13题)
(第14题)
(第15题)
14.如图,直线CD与以线段AB为直径的⊙O相切于点D,并交BA的延长线于点C,且AB=2,AD=1,点P在切线CD上移动(不与点C重合).当∠APB的度数最大时,∠ABP的度数为( )
A.15°
B.30°
C.60°
D.90°
15.如图所示,AB是⊙O的直径,弦BC=2
cm,F是弦BC的中点,∠ABC=60°.若动点E以2
cm/s的速度从A点出发沿着A→B→A的方向运动,设运动时间为t
s(0≤t<3),连接EF,当△BEF是直角三角形时,t的值为( )
A.
B.1
C.或1
D.或1或
16.如图所示,A点在半径为2的⊙O上,过线段OA上的一点P(异于A点)作直线l,与⊙O过A的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图像大致是( )
(第16题)
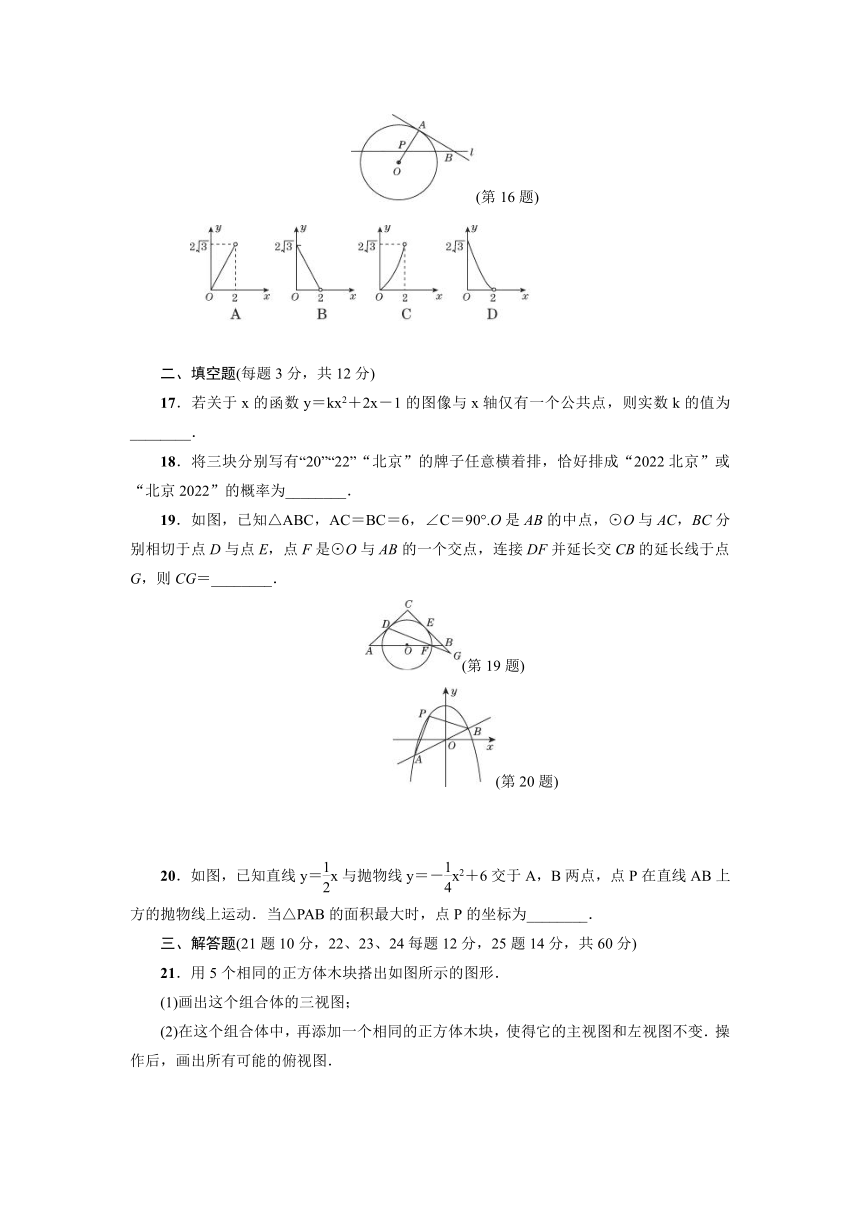
二、填空题(每题3分,共12分)
17.若关于x的函数y=kx2+2x-1的图像与x轴仅有一个公共点,则实数k的值为________.
18.将三块分别写有“20”“22”“北京”的牌子任意横着排,恰好排成“2022北京”或“北京2022”的概率为________.
19.如图,已知△ABC,AC=BC=6,∠C=90°.O是AB的中点,⊙O与AC,BC分别相切于点D与点E,点F是⊙O与AB的一个交点,连接DF并延长交CB的延长线于点G,则CG=________.
(第19题)
(第20题)
20.如图,已知直线y=x与抛物线y=-x2+6交于A,B两点,点P在直线AB上方的抛物线上运动.当△PAB的面积最大时,点P的坐标为________.
三、解答题(21题10分,22、23、24每题12分,25题14分,共60分)
21.用5个相同的正方体木块搭出如图所示的图形.
(1)画出这个组合体的三视图;
(2)在这个组合体中,再添加一个相同的正方体木块,使得它的主视图和左视图不变.操作后,画出所有可能的俯视图.
(第21题)
22.某中学要在全校学生中举办“中国梦·我的梦”主题演讲比赛,要求每班选一名代表参赛.九年级
(1)班经过投票初选,小亮和小丽票数并列班级第一,现在他们都想代表本班参赛.经班长与他们协商决定,用他们学过的掷骰子游戏来确定谁去参赛(胜者参赛).
规则如下:两人同时随机各掷一枚完全相同且质地均匀的骰子一次,向上一面的点数都是奇数,则小亮胜;向上一面的点数都是偶数,则小丽胜;否则,视为平局.若为平局,继续上述游戏,直至分出胜负为止.
如果小亮和小丽按上述规则各掷一次骰子,那么请你解答下列问题:
(1)小亮掷得向上一面的点数为奇数的概率是多少?
(2)该游戏是否公平?请用列表或画树形图等方法说明理由.
(骰子:六个面上分别刻有1,2,3,4,5,6个小圆点的小正方体)
23.已知:平面直角坐标系中,四边形OABC的顶点分别为O(0,0),A(5,0),B(m,2),C(m-5,2).
(1)问:是否存在这样的m,使得在边BC上总存在点P,使∠OPA=90°?若存在,求出m的取值范围;若不存在,请说明理由.
(2)当∠AOC与∠OAB的平分线的交点Q在边BC上时,求m的值.
24.某工厂生产一种合金薄板(其厚度忽略不计),这些薄板的形状均为正方形,边长(单位:cm)在5~50之间,每张薄板的成本价(单位:元)与它的面积(单位:cm2)成正比例,每张薄板的出厂价(单位:元)由基础价和浮动价两部分组成,其中基础价与薄板的大小无关,是固定不变的,浮动价与薄板的边长成正比例.在营销过程中得到了下面表格中的数据.
薄板的边长/cm
20
30
出厂价/(元/张)
50
70
(1)求一张薄板的出厂价与边长之间满足的函数关系式;
(2)已知出厂一张边长为40
cm的薄板,获得的利润是26元(利润=出厂价-成本价).
①求一张薄板的利润与边长之间满足的函数关系式;
②当边长为多少时,出厂一张薄板获得的利润最大?最大利润是多少?
参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标是.
25.如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为,且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
(1)求抛物线的表达式及A,B两点的坐标.
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值;若不存在,请说明理由;
(3)在以AB为直径的⊙M中,CE与⊙M相切于点E,CE交x轴于点D,求直线CE的表达式.
(第25题)
答案
一、1.B 2.B 3.C
4.B 点拨:S=EH2=x2+(1-x)2=2x2-2x+1,x的取值范围是05.B
6.C 点拨:设正方形ABCD的边长为a,则正方形ABCD的面积为a2.易知AE=OE=BE=a,所以正方形EOFB的面积为a2.又易知AN
=MN=CM=AC=a,所以正方形MHGN的面积为a2,所以P(小鸟落在花圃上)==,故选C.
(第7题)
7.C 点拨:如图,设正六边形的中心是O.连接OA,OB,OC,AC,其中AC交OB于点M,则∠AOB=∠BOC=60°,∴OA=OB=AB=OC=BC,
∴四边形ABCO是菱形,∠BAO=60°,
∴∠BAC=30°.∵cos∠BAC=,
∴AM=6×=3(mm).∵四边形ABCO是菱形,∴AC=2AM=6
mm,故选C.
8.C 9.B
10.B 点拨:∵AC是⊙O的切线,
∴∠OAC=90°.又∵∠C=40°,
∴∠AOC=50°,∴∠ABD=25°.
(第11题)
11.D 点拨:如图所示,连接OB,AC,BO与AC相交于点F,在菱形OABC中,AC⊥BO,CF=AF,FO=BF,∠COB=∠BOA,又∵扇形DOE的半径为3,菱形OABC的边长为,∴FO=BF=1.5,∴cos∠FOC===,∴∠FOC=30°,∴∠EOD=2×30°=60°,∴l==π,设围成的圆锥的底面圆的半径为r,则2πr=π,解得r=,∵圆锥的母线长为3,则此圆锥的高为=.
12.C 点拨:当x=0时,两个函数的函数值都等于b,所以两个函数图像与y轴相交于同一点,故B,D选项错误;由A,C选项中抛物线开口方向向上,所以a>0,所以一次函数y=ax+b的图像经过第一、三象限,所以A选项错误,C选项正确.
13.C 点拨:由抛物线与y轴的交点位置得c>1,故①错误;∵抛物线的对称轴为直线x=-=1,∴2a+b=0,故②正确;由抛物线与x轴有两个交点,得b2-4ac>0,即b2>4ac,故③错误;令y=0,得ax2+bx+c=0,∵方程的两根分别为x1,x2,且-=1,∴x1+x2=-=2,故④正确.
14.B 点拨:连接BD.∵直线CD与以线段AB为直径的⊙O相切于点D,∴∠ADB=90°.当∠APB的度数最大时,点P和点D重合,∴∠APB=90°.∵AB=2,AD=1,∴sin
∠ABP==,∴∠ABP=30°.∴当∠APB的度数最大时,∠ABP的度数为30°.
15.D 点拨:∵AB是⊙O的直径,
∴∠ACB=90°,∵在Rt△ABC中,BC=2,∠ABC=60°,∴AB=2BC=4
cm.①当∠BFE=90°时,由∠ABC=60°,得BE=2BF=2
cm.此时AE=AB-BE=2
cm.∴点E运动的距离为2
cm或6
cm,故t=1或t=3,由0≤t<3,知t=3不合题意,舍去.∴当∠BFE=90°时,t=1.②当∠BEF=90°时,同①可求得BE=0.5
cm,此时AE=AB-BE=3.5
cm,∴点E运动的距离为3.5
cm或4.5
cm,故t=1.75或t=2.25.综上所述,当t的值为1或1.75或2.25时,△BEF是直角三角形,故选D.
16.D 点拨:因为AB与⊙O相切,所以∠BAP=90°.因为OP=x,所以AP=2-x,因为∠APB=60°,所以AB=(2-x),所以y=AB·AP=(2-x)2(0≤x<2).故选D.
二、17.0或-1 18.
(第19题)
19.3+3 点拨:如图,连接OD.因为AC=BC=6,∠C=90°,所以AB=6.因为AC是⊙O的切线,D为切点,所以OD⊥AC,所以OD∥CG.又因为点O是AB的中点,所以OD=3.因为OD∥CG,所以△ODF∽△BGF,所以==1,所以BG==3-3,所以CG=6+3-3=3+3.
20. 点拨:本题利用割补法.如图,作PM⊥x轴交AB于点M.设点P的坐标为,则点M的坐标为,故PM=-a2-a+6.由求得点A,B的横坐标分别为-6,4.S△PAB=S△PAM+S△PBM=×(6+4)×PM=-(a+1)2+,故当a=-1时,△PAB的面积最大,此时-a2+6=,所以点P的坐标为.
(第20题)
三、21.解:(1)画出的三视图如图①所示.
(2)画出的所有可能的俯视图如图②所示.
(第21题)
22.解:(1)所求概率P==.
(2)游戏公平.
理由如下:
小丽
小亮
1
2
3
4
5
6
1
(1,1)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
2
(2,1)
(2,2)
(2,3)
(2,4)
(2,5)
(2,6)
3
(3,1)
(3,2)
(3,3)
(3,4)
(3,5)
(3,6)
4
(4,1)
(4,2)
(4,3)
(4,4)
(4,5)
(4,6)
5
(5,1)
(5,2)
(5,3)
(5,4)
(5,5)
(5,6)
6
(6,1)
(6,2)
(6,3)
(6,4)
(6,5)
(6,6)
由上表可知,共有36种等可能的结果,其中小亮、小丽获胜各有9种结果,
∴P(小亮胜)==,P(小丽胜)==.
∴该游戏是公平的.
23.解:(1)存在.由题意,知:BC∥OA,以OA为直径作⊙D,与直线BC交于点E,F,如图①(简图),则∠OEA=∠OFA=90°.
过点D作DG⊥EF于G,连DE,则DE=OD=2.5,DG=2,
EG=GF,∴EG==1.5,
∴点E(1,2),点F(4,2).
∴当即1≤m≤9时,边BC上总存在这样的点P,使∠OPA=90°.
(第23题)
(2)∵BC=5=OA,BC∥OA,∴四边形OABC是平行四边形.
当Q在边BC上时,∠OQA=180°-∠QOA-∠QAO=180°-(∠COA+∠OAB)=90°,∴点Q只能是(1)中的点E或点F.
当Q在F点时,简图如图②,∵OF,AF分别是∠AOC与∠OAB的平分线,BC∥OA,∴∠CFO=∠FOA=∠FOC,∠BFA=∠FAO=∠FAB,∴CF=OC,BF=AB,∵OC=AB,∴F是BC的中点.∵F点坐标为(4,2),∴此时m的值为6.5.
当Q在E点时,同理可求得此时m的值为3.5.
综上可知,m的值为3.5或6.5.
24.解:(1)设一张薄板的边长为x
cm,它的出厂价为y元,基础价为n元,浮动价为kx元,则y=kx+n.
由表格中的数据,得解得
所以y=2x+10.
(2)①设一张薄板的利润为P元,它的成本价为mx2元,由题意,得P=y-mx2=2x+10-mx2.将x=40,P=26代入P=2x+10-mx2,得26=2×40+10-m×402,解得m=,所以P=-x2+2x+10;②因为a=-<0,所以,当x=-=-=25(x在5~50之间)时,P有最大值,P最大值===35,即出厂一张边长为25
cm的薄板获得的利润最大,最大利润是35元.
25.解:(1)由题意,设抛物线的表达式为y=a(x-4)2-(a≠0).
∵抛物线经过点C(0,2),
∴a(0-4)2-=2,
解得a=.∴y=(x-4)2-,
即y=x2-x+2.当y=0时,
x2-x+2=0,
解得x1=2,x2=6,
∴A(2,0),B(6,0).
(2)存在,由(1)知,抛物线的对称轴l为直线x
=4,因为A、B两点关于l对称,连接CB交l于点P,则AP=BP,
所以AP+CP=BC的值最小,
∵B(6,0),C(0,2),
∴OB=6,OC=2.
∴BC==2.
∴AP+CP=BC=2.
∴AP+CP的最小值为2.
(3)连接ME,∵CE是⊙M的切线,
∴CE⊥ME,∠CEM=90°.
∴∠COD=∠DEM=90°.
由题意,得OC=ME=2,
∠ODC=∠MDE,
∴△COD≌△MED.
∴OD=DE,DC=DM.设OD=x,
则CD=DM=OM-OD=4-x.
在Rt△COD中,OD2+OC2=CD2,
∴x2+22=(4-x)2.
∴x=.∴D.
设直线CE的表达式为y=kx+b′(k≠0),
∵直线CE过C(0,2),
D两点,
则解得
∴直线CE的表达式为y=-x+2.
(120分,90分钟)
题 号
一
二
三
总 分
得 分
一、选择题(每题3分,共48分)
1.若抛物线y=2xm2-4m-3+(m-5)的顶点在x轴的下方,则( )
A.m=5
B.m=-1
C.m=5或m=-1
D.m=-5
2.
在一个不透明的袋子中装有4个红球和3个黑球,它们除颜色外其他均相同,从中任意摸出一个球,则摸出黑球的概率是( )
A.
B.
C.
D.
3.如图是将正方体切去一个角后形成的几何体,则该几何体的左视图为( )
(第3题)
INCLUDEPICTURE
"../../../YXJ18.tif"
\
MERGEFORMAT
4.如图所示,正方形ABCD的边长为1,E,F,G,H分别为各边上的点(与A,B,C,D不重合),且AE=BF=CG=DH,设小正方形EFGH的面积为S,AE的长为x,则S关于x的函数图像大致是( )
(第4题)
5.一个几何体的三视图如图所示,这个几何体是( )
A.球
B.圆柱
C.圆锥
D.立方体
(第5题)
(第6题)
(第7题)
6.如图,正方形ABCD是一块绿化带,其中阴影部分EOFB,GHMN都是正方形的花圃.一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟落在花圃上的概率为( )
A.
B.
C.
D.
7.如图,要拧开一个边长为a=6
mm的正六边形螺帽,扳手张开的开口b至少为( )
A.6
mm
B.12
mm
C.6
mm
D.4
mm
8.圆心角为120°,弧长为12π的扇形半径为( )
A.6
B.9
C.18
D.36
9.如图,P是⊙O外一点,PA,PB分别和⊙O切于A,B,C是弧AB上任意一点,过C作⊙O的切线分别交PA,PB于D,E.若△PDE的周长为12,则PA等于( )
A.12
B.6
C.8
D.10
(第9题)
(第10题)
(第11题)
10.如图所示,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=40°,则∠ABD的度数是( )
A.30°
B.25°
C.20°
D.15°
11.如图所示,扇形DOE的半径为3,边长为的菱形OABC的顶点A,C,B分别在OD,OE,上,若把扇形DOE围成一个圆锥,则此圆锥的高为( )
A.
B.2
C.
D.
12.在同一坐标系内,一次函数y=ax+b与二次函数y=ax2+8x+b的图像可能是( )
13.二次函数y=ax2+bx+c(a≠0)的图像如图所示,其对称轴为直线x=1,有如下结论:①c<1;②2a+b=0;③b2<4ac;④若方程ax2+bx+c=0的两根分别为x1,x2,则x1+x2=2,其中正确的结论是( )
A.①②
B.①③
C.②④
D.③④
(第13题)
(第14题)
(第15题)
14.如图,直线CD与以线段AB为直径的⊙O相切于点D,并交BA的延长线于点C,且AB=2,AD=1,点P在切线CD上移动(不与点C重合).当∠APB的度数最大时,∠ABP的度数为( )
A.15°
B.30°
C.60°
D.90°
15.如图所示,AB是⊙O的直径,弦BC=2
cm,F是弦BC的中点,∠ABC=60°.若动点E以2
cm/s的速度从A点出发沿着A→B→A的方向运动,设运动时间为t
s(0≤t<3),连接EF,当△BEF是直角三角形时,t的值为( )
A.
B.1
C.或1
D.或1或
16.如图所示,A点在半径为2的⊙O上,过线段OA上的一点P(异于A点)作直线l,与⊙O过A的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图像大致是( )
(第16题)
二、填空题(每题3分,共12分)
17.若关于x的函数y=kx2+2x-1的图像与x轴仅有一个公共点,则实数k的值为________.
18.将三块分别写有“20”“22”“北京”的牌子任意横着排,恰好排成“2022北京”或“北京2022”的概率为________.
19.如图,已知△ABC,AC=BC=6,∠C=90°.O是AB的中点,⊙O与AC,BC分别相切于点D与点E,点F是⊙O与AB的一个交点,连接DF并延长交CB的延长线于点G,则CG=________.
(第19题)
(第20题)
20.如图,已知直线y=x与抛物线y=-x2+6交于A,B两点,点P在直线AB上方的抛物线上运动.当△PAB的面积最大时,点P的坐标为________.
三、解答题(21题10分,22、23、24每题12分,25题14分,共60分)
21.用5个相同的正方体木块搭出如图所示的图形.
(1)画出这个组合体的三视图;
(2)在这个组合体中,再添加一个相同的正方体木块,使得它的主视图和左视图不变.操作后,画出所有可能的俯视图.
(第21题)
22.某中学要在全校学生中举办“中国梦·我的梦”主题演讲比赛,要求每班选一名代表参赛.九年级
(1)班经过投票初选,小亮和小丽票数并列班级第一,现在他们都想代表本班参赛.经班长与他们协商决定,用他们学过的掷骰子游戏来确定谁去参赛(胜者参赛).
规则如下:两人同时随机各掷一枚完全相同且质地均匀的骰子一次,向上一面的点数都是奇数,则小亮胜;向上一面的点数都是偶数,则小丽胜;否则,视为平局.若为平局,继续上述游戏,直至分出胜负为止.
如果小亮和小丽按上述规则各掷一次骰子,那么请你解答下列问题:
(1)小亮掷得向上一面的点数为奇数的概率是多少?
(2)该游戏是否公平?请用列表或画树形图等方法说明理由.
(骰子:六个面上分别刻有1,2,3,4,5,6个小圆点的小正方体)
23.已知:平面直角坐标系中,四边形OABC的顶点分别为O(0,0),A(5,0),B(m,2),C(m-5,2).
(1)问:是否存在这样的m,使得在边BC上总存在点P,使∠OPA=90°?若存在,求出m的取值范围;若不存在,请说明理由.
(2)当∠AOC与∠OAB的平分线的交点Q在边BC上时,求m的值.
24.某工厂生产一种合金薄板(其厚度忽略不计),这些薄板的形状均为正方形,边长(单位:cm)在5~50之间,每张薄板的成本价(单位:元)与它的面积(单位:cm2)成正比例,每张薄板的出厂价(单位:元)由基础价和浮动价两部分组成,其中基础价与薄板的大小无关,是固定不变的,浮动价与薄板的边长成正比例.在营销过程中得到了下面表格中的数据.
薄板的边长/cm
20
30
出厂价/(元/张)
50
70
(1)求一张薄板的出厂价与边长之间满足的函数关系式;
(2)已知出厂一张边长为40
cm的薄板,获得的利润是26元(利润=出厂价-成本价).
①求一张薄板的利润与边长之间满足的函数关系式;
②当边长为多少时,出厂一张薄板获得的利润最大?最大利润是多少?
参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标是.
25.如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为,且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
(1)求抛物线的表达式及A,B两点的坐标.
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值;若不存在,请说明理由;
(3)在以AB为直径的⊙M中,CE与⊙M相切于点E,CE交x轴于点D,求直线CE的表达式.
(第25题)
答案
一、1.B 2.B 3.C
4.B 点拨:S=EH2=x2+(1-x)2=2x2-2x+1,x的取值范围是0
6.C 点拨:设正方形ABCD的边长为a,则正方形ABCD的面积为a2.易知AE=OE=BE=a,所以正方形EOFB的面积为a2.又易知AN
=MN=CM=AC=a,所以正方形MHGN的面积为a2,所以P(小鸟落在花圃上)==,故选C.
(第7题)
7.C 点拨:如图,设正六边形的中心是O.连接OA,OB,OC,AC,其中AC交OB于点M,则∠AOB=∠BOC=60°,∴OA=OB=AB=OC=BC,
∴四边形ABCO是菱形,∠BAO=60°,
∴∠BAC=30°.∵cos∠BAC=,
∴AM=6×=3(mm).∵四边形ABCO是菱形,∴AC=2AM=6
mm,故选C.
8.C 9.B
10.B 点拨:∵AC是⊙O的切线,
∴∠OAC=90°.又∵∠C=40°,
∴∠AOC=50°,∴∠ABD=25°.
(第11题)
11.D 点拨:如图所示,连接OB,AC,BO与AC相交于点F,在菱形OABC中,AC⊥BO,CF=AF,FO=BF,∠COB=∠BOA,又∵扇形DOE的半径为3,菱形OABC的边长为,∴FO=BF=1.5,∴cos∠FOC===,∴∠FOC=30°,∴∠EOD=2×30°=60°,∴l==π,设围成的圆锥的底面圆的半径为r,则2πr=π,解得r=,∵圆锥的母线长为3,则此圆锥的高为=.
12.C 点拨:当x=0时,两个函数的函数值都等于b,所以两个函数图像与y轴相交于同一点,故B,D选项错误;由A,C选项中抛物线开口方向向上,所以a>0,所以一次函数y=ax+b的图像经过第一、三象限,所以A选项错误,C选项正确.
13.C 点拨:由抛物线与y轴的交点位置得c>1,故①错误;∵抛物线的对称轴为直线x=-=1,∴2a+b=0,故②正确;由抛物线与x轴有两个交点,得b2-4ac>0,即b2>4ac,故③错误;令y=0,得ax2+bx+c=0,∵方程的两根分别为x1,x2,且-=1,∴x1+x2=-=2,故④正确.
14.B 点拨:连接BD.∵直线CD与以线段AB为直径的⊙O相切于点D,∴∠ADB=90°.当∠APB的度数最大时,点P和点D重合,∴∠APB=90°.∵AB=2,AD=1,∴sin
∠ABP==,∴∠ABP=30°.∴当∠APB的度数最大时,∠ABP的度数为30°.
15.D 点拨:∵AB是⊙O的直径,
∴∠ACB=90°,∵在Rt△ABC中,BC=2,∠ABC=60°,∴AB=2BC=4
cm.①当∠BFE=90°时,由∠ABC=60°,得BE=2BF=2
cm.此时AE=AB-BE=2
cm.∴点E运动的距离为2
cm或6
cm,故t=1或t=3,由0≤t<3,知t=3不合题意,舍去.∴当∠BFE=90°时,t=1.②当∠BEF=90°时,同①可求得BE=0.5
cm,此时AE=AB-BE=3.5
cm,∴点E运动的距离为3.5
cm或4.5
cm,故t=1.75或t=2.25.综上所述,当t的值为1或1.75或2.25时,△BEF是直角三角形,故选D.
16.D 点拨:因为AB与⊙O相切,所以∠BAP=90°.因为OP=x,所以AP=2-x,因为∠APB=60°,所以AB=(2-x),所以y=AB·AP=(2-x)2(0≤x<2).故选D.
二、17.0或-1 18.
(第19题)
19.3+3 点拨:如图,连接OD.因为AC=BC=6,∠C=90°,所以AB=6.因为AC是⊙O的切线,D为切点,所以OD⊥AC,所以OD∥CG.又因为点O是AB的中点,所以OD=3.因为OD∥CG,所以△ODF∽△BGF,所以==1,所以BG==3-3,所以CG=6+3-3=3+3.
20. 点拨:本题利用割补法.如图,作PM⊥x轴交AB于点M.设点P的坐标为,则点M的坐标为,故PM=-a2-a+6.由求得点A,B的横坐标分别为-6,4.S△PAB=S△PAM+S△PBM=×(6+4)×PM=-(a+1)2+,故当a=-1时,△PAB的面积最大,此时-a2+6=,所以点P的坐标为.
(第20题)
三、21.解:(1)画出的三视图如图①所示.
(2)画出的所有可能的俯视图如图②所示.
(第21题)
22.解:(1)所求概率P==.
(2)游戏公平.
理由如下:
小丽
小亮
1
2
3
4
5
6
1
(1,1)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
2
(2,1)
(2,2)
(2,3)
(2,4)
(2,5)
(2,6)
3
(3,1)
(3,2)
(3,3)
(3,4)
(3,5)
(3,6)
4
(4,1)
(4,2)
(4,3)
(4,4)
(4,5)
(4,6)
5
(5,1)
(5,2)
(5,3)
(5,4)
(5,5)
(5,6)
6
(6,1)
(6,2)
(6,3)
(6,4)
(6,5)
(6,6)
由上表可知,共有36种等可能的结果,其中小亮、小丽获胜各有9种结果,
∴P(小亮胜)==,P(小丽胜)==.
∴该游戏是公平的.
23.解:(1)存在.由题意,知:BC∥OA,以OA为直径作⊙D,与直线BC交于点E,F,如图①(简图),则∠OEA=∠OFA=90°.
过点D作DG⊥EF于G,连DE,则DE=OD=2.5,DG=2,
EG=GF,∴EG==1.5,
∴点E(1,2),点F(4,2).
∴当即1≤m≤9时,边BC上总存在这样的点P,使∠OPA=90°.
(第23题)
(2)∵BC=5=OA,BC∥OA,∴四边形OABC是平行四边形.
当Q在边BC上时,∠OQA=180°-∠QOA-∠QAO=180°-(∠COA+∠OAB)=90°,∴点Q只能是(1)中的点E或点F.
当Q在F点时,简图如图②,∵OF,AF分别是∠AOC与∠OAB的平分线,BC∥OA,∴∠CFO=∠FOA=∠FOC,∠BFA=∠FAO=∠FAB,∴CF=OC,BF=AB,∵OC=AB,∴F是BC的中点.∵F点坐标为(4,2),∴此时m的值为6.5.
当Q在E点时,同理可求得此时m的值为3.5.
综上可知,m的值为3.5或6.5.
24.解:(1)设一张薄板的边长为x
cm,它的出厂价为y元,基础价为n元,浮动价为kx元,则y=kx+n.
由表格中的数据,得解得
所以y=2x+10.
(2)①设一张薄板的利润为P元,它的成本价为mx2元,由题意,得P=y-mx2=2x+10-mx2.将x=40,P=26代入P=2x+10-mx2,得26=2×40+10-m×402,解得m=,所以P=-x2+2x+10;②因为a=-<0,所以,当x=-=-=25(x在5~50之间)时,P有最大值,P最大值===35,即出厂一张边长为25
cm的薄板获得的利润最大,最大利润是35元.
25.解:(1)由题意,设抛物线的表达式为y=a(x-4)2-(a≠0).
∵抛物线经过点C(0,2),
∴a(0-4)2-=2,
解得a=.∴y=(x-4)2-,
即y=x2-x+2.当y=0时,
x2-x+2=0,
解得x1=2,x2=6,
∴A(2,0),B(6,0).
(2)存在,由(1)知,抛物线的对称轴l为直线x
=4,因为A、B两点关于l对称,连接CB交l于点P,则AP=BP,
所以AP+CP=BC的值最小,
∵B(6,0),C(0,2),
∴OB=6,OC=2.
∴BC==2.
∴AP+CP=BC=2.
∴AP+CP的最小值为2.
(3)连接ME,∵CE是⊙M的切线,
∴CE⊥ME,∠CEM=90°.
∴∠COD=∠DEM=90°.
由题意,得OC=ME=2,
∠ODC=∠MDE,
∴△COD≌△MED.
∴OD=DE,DC=DM.设OD=x,
则CD=DM=OM-OD=4-x.
在Rt△COD中,OD2+OC2=CD2,
∴x2+22=(4-x)2.
∴x=.∴D.
设直线CE的表达式为y=kx+b′(k≠0),
∵直线CE过C(0,2),
D两点,
则解得
∴直线CE的表达式为y=-x+2.
同课章节目录
