2017-2018年青岛版八年级上第5章几何证明初步检测试卷(附答案)
文档属性
| 名称 | 2017-2018年青岛版八年级上第5章几何证明初步检测试卷(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 293.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-21 15:57:07 | ||
图片预览

文档简介
第五章检测题
(时间:90分钟,满分:100分)
一、选择题(每小题3分,共30分)
1.
下列语句中,不是命题的是( )
A.若两角之和为90°,则这两个角互补
B.同角的余角相等
C.作线段的垂直平分线
D.相等的角是对顶角
2.
下列语句中属于定义的是( )
A.直角都相等
B.作已知角的平分线
C.连接两点的线段的长度,叫做这两点间的距离
D.两点之间,线段最短
3.
下面关于定理的说法不正确的是( )
A.定理是真命题
B.定理的正确性不需要证明
C.定理可以作为推理论证的依据
D.定理的正确性需证明
4.
如图,在等边△中,,则等于( )
A.
B.
C.
D.
5.
如图,已知,,,结论:①;②;
③;④△≌△.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
6.
对于图中标记的各角,下列条件能够推理得到∥的是( )
A.∠1=∠2
B.
∠2=∠4
C.
∠3=∠4
D.∠1+∠4=180°
7.如图,∥,,若,
则等于( )
A.
B.
C.
D.
8.
如图,在四边形ABCD中,AC垂直平分BD,垂足为E,下列结论
不一定成立的是(
)
A.AB=AD
B.CA平分∠BCD
C.AB=BD
D.△BEC≌△DEC
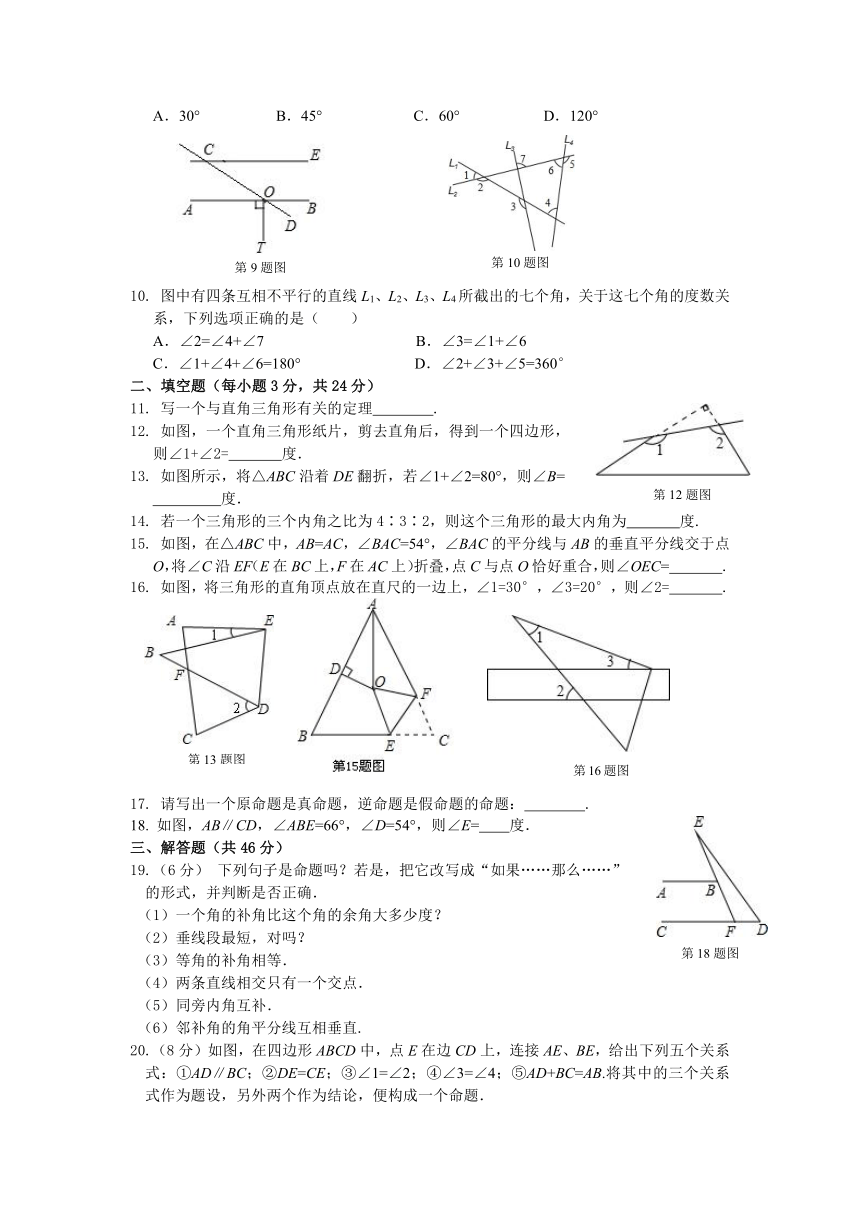
9.
如图,直线AB、CD交于点O,OT⊥AB于O,CE∥AB交CD于点C,若∠ECO=30°,则∠DOT等于( )
A.30°
B.45°
C.60°
D.120°
10.
图中有四条互相不平行的直线L1、L2、L3、L4所截出的七个角,关于这七个角的度数关系,下列选项正确的是( )
A.∠2=∠4+∠7
B.∠3=∠1+∠6
C.∠1+∠4+∠6=180°
D.∠2+∠3+∠5=360°
二、填空题(每小题3分,共24分)
11.
写一个与直角三角形有关的定理
.
12.
如图,一个直角三角形纸片,剪去直角后,得到一个四边形,
则∠1+∠2=
度.
13.
如图所示,将△ABC沿着DE翻折,若∠1+∠2=80°,则∠B=
度.
14.
若一个三角形的三个内角之比为4∶3∶2,则这个三角形的最大内角为
度.
15.
如图,在△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC=
.
16.
如图,将三角形的直角顶点放在直尺的一边上,∠1=30°,∠3=20°,则∠2=
.
17.
请写出一个原命题是真命题,逆命题是假命题的命题:
.
18.
如图,AB∥CD,∠ABE=66°,∠D=54°,则∠E=
度.
三、解答题(共46分)
19.(6分)
下列句子是命题吗?若是,把它改写成“如果……那么……”
的形式,并判断是否正确.
(1)一个角的补角比这个角的余角大多少度?
(2)垂线段最短,对吗?
(3)等角的补角相等.
(4)两条直线相交只有一个交点.
(5)同旁内角互补.
(6)邻补角的角平分线互相垂直.
20.(8分)如图,在四边形ABCD中,点E在边CD上,连接AE、BE,给出下列五个关系式:①AD∥BC;②DE=CE;③∠1=∠2;④∠3=∠4;⑤AD+BC=AB.将其中的三个关系式作为题设,另外两个作为结论,便构成一个命题.
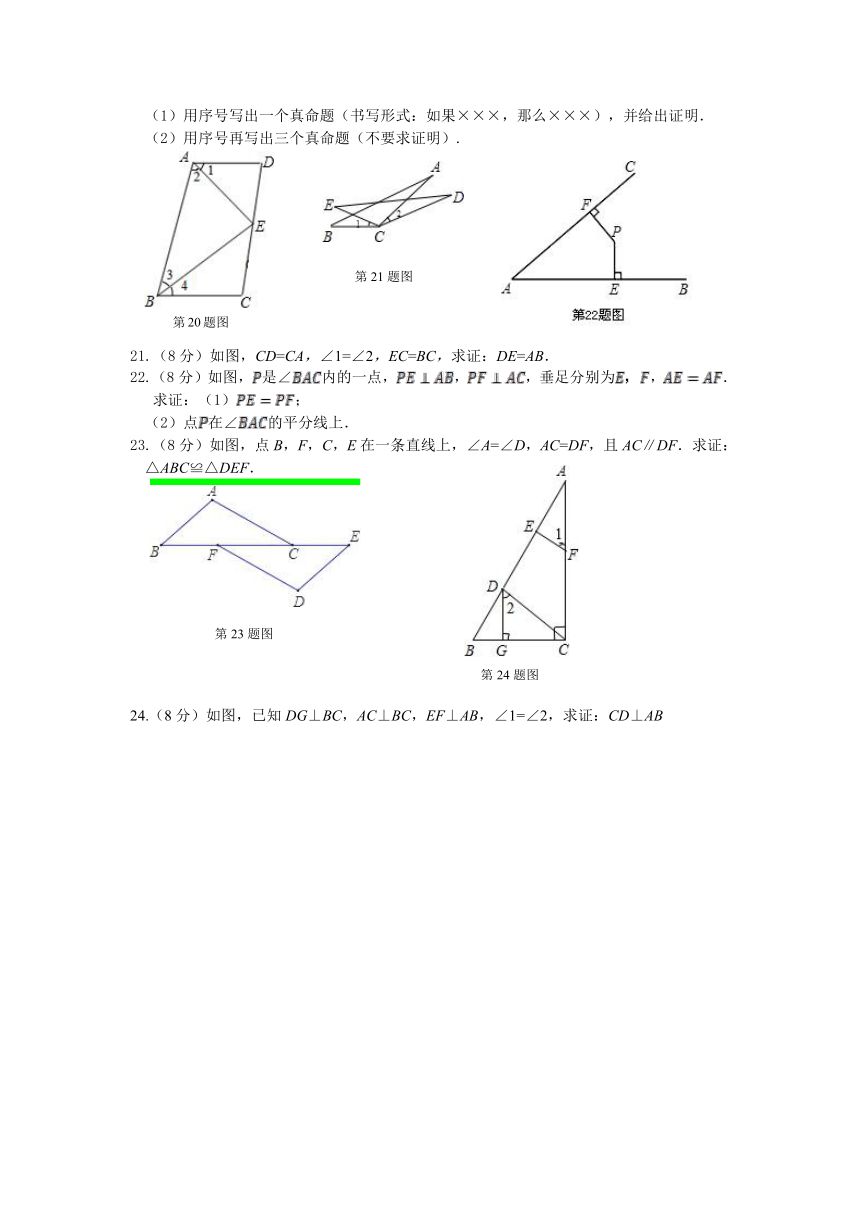
(1)用序号写出一个真命题(书写形式:如果×××,那么×××),并给出证明.
(2)用序号再写出三个真命题(不要求证明).
21.(8分)如图,CD=CA,∠1=∠2,EC=BC,求证:DE=AB.
22.(8分)如图,是∠内的一点,,,垂足分别为,.
求证:(1);
(2)点在∠的平分线上.
23.(8分)如图,点B,F,C,E在一条直线上,∠A=∠D,AC=DF,且AC∥DF.求证:△ABC≌△DEF.
24.(8分)如图,已知DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB
参考答案
1.
C
解析:根据命题的定义,可知A、B、D都是命题,而C属于作图语言,不是命题.
故选C.
2.
C
解析:A是直角的性质,不是定义;B是作图语言,不是定义;C是定义;D是公理,不是定义.故选C.
3.
B
解析:根据定理的定义,可知A,C,D是正确的,B是错误的.故选B.
4.C
解析:在等边△中,有,.
又因为,所以△≌△,所以.
所以.故选C.
5.
C
解析:因为,,,所以
△≌△(AAS),
所以,所以
,即故③正确.
又因为,,所以△≌△(ASA).所以
.故①正确.
由△≌△,知,又因为,,
所以△≌△,故④正确.
由于条件不足,无法证得②故正确的结论有:①③④.
6.
D
解析:A.∠1与∠2是邻角,不是被第三条直线所截得的同位角或内错角,不能推出平行;
B.∠2+∠3与∠4是被截得的同位角,而∠2与∠4不是,不能推出平行;
C.∠3与∠4,不是被截得的同位角,不能推出平行;
D.∠1+∠4=180°,∠1的对顶角与∠4是被截得的同旁内角,能推出平行.故选D.
7.
C
解析:因为∥,所以.
因为,所以.
如图,过点作∠∠交于点,则△≌△,
所以,
因为,
所以.
8.
C
解析:∵
AC垂直平分BD,∴
AB=AD,BC=DC,∠BCE=∠DCE,
∴
CA平分∠BCD.AB与BD不一定相等,故选C.
9.C
解析:∵
CE∥AB,∴
∠DOB=∠ECO=30°.
∵
OT⊥AB,∴
∠BOT=90°,
∴
∠DOT=∠BOT-∠DOB=90°-30°=60°.故选C.
10.C
解析:根据四条互相不平行的直线L1、L2、L3、L4所截出的七个角,
可知∠1+∠4+∠6=180°.故选C.
11.直角三角形两直角边的平方和等于斜边的平方
解析:本题是一道开放型题目,只要保证命题是真命题即可.
12.270
解析:如图,根据题意可知∠5=90°,∴
∠3+∠4=90°,
∴
∠1+∠2=180°+180°-(∠3+∠4)=360°-90°=270°.
13.40
解析:∵
△ABC沿着DE翻折,
∴
∠1+2∠BED=180°,∠2+2∠BDE=180°,
∴
∠1+∠2+2(∠BED+∠BDE)=360°,
而∠1+∠2=80°,∠B+∠BED+∠BDE=180°,
∴
80°+2(180°-∠B)=360°,
∴
∠B=40°.
14.80
解析:这个三角形的最大内角为180°×=80°.
15.
108°
解析:如图,连接OB,OC.
∵
∠BAC=54°,AO为∠BAC的平分线,
∴
又∵
AB=AC,
∴
.
∵
DO是AB的垂直平分线,
∴
OA=OB,
∴
∠ABO=∠BAO=27°,
∴
∠OBC=∠ABC-∠ABO=63°-27°=36°.
∵
DO是AB的垂直平分线,AO为∠BAC的平分线,
∴
点O是△ABC的外心,
∴
OB=OC,
∴
∠OCB=∠OBC=36°,
∵
将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,
∴
OE=CE,
∴
∠COE=∠OCB=36°.
在△OCE中,∠OEC=180°-∠COE-∠OCB=180°-36°-36°=108°.
16.
50°
解析:如图,由三角形的外角性质可得∠4=∠1+∠3=50°,∵
∠2和∠4是两平行线间的内错角,∴
∠2=∠4=50°.
17.
对顶角相等(答案不唯一)
解析:本题是一道开放性题目,答案不唯一,只要符合条件即可.把一个命题的条件和结论互换就得到它的逆命题.正确的命题叫真命题,错误的命题叫假命题.
18.
12
解析:∵
AB∥CD,∴
∠BFC=∠ABE=66°.
在△EFD中,利用三角形的外角等于与它不相邻的两个内角的和,得到∠BFC=∠E+∠D,
∴
∠E=∠BFC-∠D=12°.
19.分析:根据命题的定义先判断出哪些是命题,再把命题的题设写在“如果”后面,结论放在“那么”后面.
解:对一件事情做出判断的句子是命题,因为(1)(2)是问句,所以(1)(2)不是命题,其余4个都是命题.
(3)如果两个角相等,那么它们的补角相等,正确;
(4)如果两条直线相交,那么它们只有一个交点,正确;
(5)如果两个角是同旁内角,那么它们互补,错误;
(6)如果两条射线是邻补角的角平分线,那么它们互相垂直,正确.
20.分析:(1)如果①②③,那么④⑤.过E点作EF∥AD,与AB交于点F,根据平行线的性质推出EF为梯形ABCD的中位线,根据平行线的性质和等量代换,即可推出∠4=∠3,AB=2EF,通过2EF=AD+BC,即可推出AB=AD+BC.(2)根据真命题的定义,写出命题即可.
解:(1)如果①②③,那么④⑤.
证明如下:如图,过E点作EF∥AD,与AB交于点F.
∵
AD∥BC,∴
EF∥BC.∵
DE=CE,∴
AF=BF.
即EF为梯形ABCD的中位线,∴
2EF=AD+BC,
∴
∠1=∠AEF,∠4=∠FEB.
∵
∠1=∠2,∴
∠2=∠AEF,∴
AF=EF.
∵
AF=BF,∴
BF=EF,∴
∠3=∠FEB,∴
∠4=∠3.
∵
AB=AF+BF,∴
AB=2EF.∵
2EF=AD+BC,∴
AB=AD+BC.
(2)如果①②④,那么③⑤;如果①③④,那么②⑤;如果①②⑤,那么③④.
21.分析:根据三角形全等的判定,由已知先证∠ACB=∠DCE,再根据SAS可证△ABC≌△DEC,继而可得出结论.
证明:∵
∠1=∠2,∴
∠1+∠ECA=∠2+∠ACE,
即∠ACB=∠DCE.
在△ABC和△DEC中,∵
CA=CD,∠ACB=∠DCE,BC=EC,
∴
△ABC≌△DEC(SAS).∴
DE=AB.
22.分析:(1)连接AP,根据HL证明△APF≌△APE,可得到PE=PF;
(2)利用(1)中的全等,可得出∠FAP=∠EAP,那么点P在∠BAC的平分线上.
证明:(1)如图,连接AP并延长,
∵
PE⊥AB,PF⊥AC,
∴
∠AEP=∠AFP=90°.
在Rt△AEP和Rt△AFP中,AE=AF,AP=AP,
∴
Rt△AEP≌Rt△AFP(HL),
∴
PE=PF.
(2)∵
Rt△AEP≌Rt△AFP,
∴
∠EAP=∠FAP,
∴
AP是∠BAC的角平分线,
故点P在∠BAC的角平分线上.
23.分析:利用ASA证明两个三角形全等即可.
证明:∵
AC∥DF,∴
∠ACB=∠DFE.
在△ABC和△DEF中,
∠A=∠D,AC=DF,∠ACB=∠DFE,
∴
△ABC≌△DEF.
24.分析:灵活运用垂直的定义,注意由垂直可得90°角,由90°角可得垂直,结合平行线的判定和性质,只要证得∠ADC=90°,即可得CD⊥AB.
证明:∵
DG⊥BC,AC⊥BC(已知),
∴
∠DGB=∠ACB=90°(垂直的定义),
∴
DG∥AC(同位角相等,两直线平行).
∴
∠2=∠ACD(两直线平行,内错角相等).
∵
∠1=∠2(已知),∴
∠1=∠ACD(等量代换),
∴
EF∥CD(同位角相等,两直线平行).
∴
∠AEF=∠ADC(两直线平行,同位角相等).
∵
EF⊥AB(已知),∴
∠AEF=90°(垂直的定义),
∴
∠ADC=90°(等量代换).
∴
CD⊥AB(垂直的定义).
第6题图
第10题图
第9题图
第12题图
第16题图
第13题图
第18题图
第21题图
第20题图
第24题图
第23题图
第12题答图
第16题答图
第20题答图
(时间:90分钟,满分:100分)
一、选择题(每小题3分,共30分)
1.
下列语句中,不是命题的是( )
A.若两角之和为90°,则这两个角互补
B.同角的余角相等
C.作线段的垂直平分线
D.相等的角是对顶角
2.
下列语句中属于定义的是( )
A.直角都相等
B.作已知角的平分线
C.连接两点的线段的长度,叫做这两点间的距离
D.两点之间,线段最短
3.
下面关于定理的说法不正确的是( )
A.定理是真命题
B.定理的正确性不需要证明
C.定理可以作为推理论证的依据
D.定理的正确性需证明
4.
如图,在等边△中,,则等于( )
A.
B.
C.
D.
5.
如图,已知,,,结论:①;②;
③;④△≌△.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
6.
对于图中标记的各角,下列条件能够推理得到∥的是( )
A.∠1=∠2
B.
∠2=∠4
C.
∠3=∠4
D.∠1+∠4=180°
7.如图,∥,,若,
则等于( )
A.
B.
C.
D.
8.
如图,在四边形ABCD中,AC垂直平分BD,垂足为E,下列结论
不一定成立的是(
)
A.AB=AD
B.CA平分∠BCD
C.AB=BD
D.△BEC≌△DEC
9.
如图,直线AB、CD交于点O,OT⊥AB于O,CE∥AB交CD于点C,若∠ECO=30°,则∠DOT等于( )
A.30°
B.45°
C.60°
D.120°
10.
图中有四条互相不平行的直线L1、L2、L3、L4所截出的七个角,关于这七个角的度数关系,下列选项正确的是( )
A.∠2=∠4+∠7
B.∠3=∠1+∠6
C.∠1+∠4+∠6=180°
D.∠2+∠3+∠5=360°
二、填空题(每小题3分,共24分)
11.
写一个与直角三角形有关的定理
.
12.
如图,一个直角三角形纸片,剪去直角后,得到一个四边形,
则∠1+∠2=
度.
13.
如图所示,将△ABC沿着DE翻折,若∠1+∠2=80°,则∠B=
度.
14.
若一个三角形的三个内角之比为4∶3∶2,则这个三角形的最大内角为
度.
15.
如图,在△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC=
.
16.
如图,将三角形的直角顶点放在直尺的一边上,∠1=30°,∠3=20°,则∠2=
.
17.
请写出一个原命题是真命题,逆命题是假命题的命题:
.
18.
如图,AB∥CD,∠ABE=66°,∠D=54°,则∠E=
度.
三、解答题(共46分)
19.(6分)
下列句子是命题吗?若是,把它改写成“如果……那么……”
的形式,并判断是否正确.
(1)一个角的补角比这个角的余角大多少度?
(2)垂线段最短,对吗?
(3)等角的补角相等.
(4)两条直线相交只有一个交点.
(5)同旁内角互补.
(6)邻补角的角平分线互相垂直.
20.(8分)如图,在四边形ABCD中,点E在边CD上,连接AE、BE,给出下列五个关系式:①AD∥BC;②DE=CE;③∠1=∠2;④∠3=∠4;⑤AD+BC=AB.将其中的三个关系式作为题设,另外两个作为结论,便构成一个命题.
(1)用序号写出一个真命题(书写形式:如果×××,那么×××),并给出证明.
(2)用序号再写出三个真命题(不要求证明).
21.(8分)如图,CD=CA,∠1=∠2,EC=BC,求证:DE=AB.
22.(8分)如图,是∠内的一点,,,垂足分别为,.
求证:(1);
(2)点在∠的平分线上.
23.(8分)如图,点B,F,C,E在一条直线上,∠A=∠D,AC=DF,且AC∥DF.求证:△ABC≌△DEF.
24.(8分)如图,已知DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB
参考答案
1.
C
解析:根据命题的定义,可知A、B、D都是命题,而C属于作图语言,不是命题.
故选C.
2.
C
解析:A是直角的性质,不是定义;B是作图语言,不是定义;C是定义;D是公理,不是定义.故选C.
3.
B
解析:根据定理的定义,可知A,C,D是正确的,B是错误的.故选B.
4.C
解析:在等边△中,有,.
又因为,所以△≌△,所以.
所以.故选C.
5.
C
解析:因为,,,所以
△≌△(AAS),
所以,所以
,即故③正确.
又因为,,所以△≌△(ASA).所以
.故①正确.
由△≌△,知,又因为,,
所以△≌△,故④正确.
由于条件不足,无法证得②故正确的结论有:①③④.
6.
D
解析:A.∠1与∠2是邻角,不是被第三条直线所截得的同位角或内错角,不能推出平行;
B.∠2+∠3与∠4是被截得的同位角,而∠2与∠4不是,不能推出平行;
C.∠3与∠4,不是被截得的同位角,不能推出平行;
D.∠1+∠4=180°,∠1的对顶角与∠4是被截得的同旁内角,能推出平行.故选D.
7.
C
解析:因为∥,所以.
因为,所以.
如图,过点作∠∠交于点,则△≌△,
所以,
因为,
所以.
8.
C
解析:∵
AC垂直平分BD,∴
AB=AD,BC=DC,∠BCE=∠DCE,
∴
CA平分∠BCD.AB与BD不一定相等,故选C.
9.C
解析:∵
CE∥AB,∴
∠DOB=∠ECO=30°.
∵
OT⊥AB,∴
∠BOT=90°,
∴
∠DOT=∠BOT-∠DOB=90°-30°=60°.故选C.
10.C
解析:根据四条互相不平行的直线L1、L2、L3、L4所截出的七个角,
可知∠1+∠4+∠6=180°.故选C.
11.直角三角形两直角边的平方和等于斜边的平方
解析:本题是一道开放型题目,只要保证命题是真命题即可.
12.270
解析:如图,根据题意可知∠5=90°,∴
∠3+∠4=90°,
∴
∠1+∠2=180°+180°-(∠3+∠4)=360°-90°=270°.
13.40
解析:∵
△ABC沿着DE翻折,
∴
∠1+2∠BED=180°,∠2+2∠BDE=180°,
∴
∠1+∠2+2(∠BED+∠BDE)=360°,
而∠1+∠2=80°,∠B+∠BED+∠BDE=180°,
∴
80°+2(180°-∠B)=360°,
∴
∠B=40°.
14.80
解析:这个三角形的最大内角为180°×=80°.
15.
108°
解析:如图,连接OB,OC.
∵
∠BAC=54°,AO为∠BAC的平分线,
∴
又∵
AB=AC,
∴
.
∵
DO是AB的垂直平分线,
∴
OA=OB,
∴
∠ABO=∠BAO=27°,
∴
∠OBC=∠ABC-∠ABO=63°-27°=36°.
∵
DO是AB的垂直平分线,AO为∠BAC的平分线,
∴
点O是△ABC的外心,
∴
OB=OC,
∴
∠OCB=∠OBC=36°,
∵
将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,
∴
OE=CE,
∴
∠COE=∠OCB=36°.
在△OCE中,∠OEC=180°-∠COE-∠OCB=180°-36°-36°=108°.
16.
50°
解析:如图,由三角形的外角性质可得∠4=∠1+∠3=50°,∵
∠2和∠4是两平行线间的内错角,∴
∠2=∠4=50°.
17.
对顶角相等(答案不唯一)
解析:本题是一道开放性题目,答案不唯一,只要符合条件即可.把一个命题的条件和结论互换就得到它的逆命题.正确的命题叫真命题,错误的命题叫假命题.
18.
12
解析:∵
AB∥CD,∴
∠BFC=∠ABE=66°.
在△EFD中,利用三角形的外角等于与它不相邻的两个内角的和,得到∠BFC=∠E+∠D,
∴
∠E=∠BFC-∠D=12°.
19.分析:根据命题的定义先判断出哪些是命题,再把命题的题设写在“如果”后面,结论放在“那么”后面.
解:对一件事情做出判断的句子是命题,因为(1)(2)是问句,所以(1)(2)不是命题,其余4个都是命题.
(3)如果两个角相等,那么它们的补角相等,正确;
(4)如果两条直线相交,那么它们只有一个交点,正确;
(5)如果两个角是同旁内角,那么它们互补,错误;
(6)如果两条射线是邻补角的角平分线,那么它们互相垂直,正确.
20.分析:(1)如果①②③,那么④⑤.过E点作EF∥AD,与AB交于点F,根据平行线的性质推出EF为梯形ABCD的中位线,根据平行线的性质和等量代换,即可推出∠4=∠3,AB=2EF,通过2EF=AD+BC,即可推出AB=AD+BC.(2)根据真命题的定义,写出命题即可.
解:(1)如果①②③,那么④⑤.
证明如下:如图,过E点作EF∥AD,与AB交于点F.
∵
AD∥BC,∴
EF∥BC.∵
DE=CE,∴
AF=BF.
即EF为梯形ABCD的中位线,∴
2EF=AD+BC,
∴
∠1=∠AEF,∠4=∠FEB.
∵
∠1=∠2,∴
∠2=∠AEF,∴
AF=EF.
∵
AF=BF,∴
BF=EF,∴
∠3=∠FEB,∴
∠4=∠3.
∵
AB=AF+BF,∴
AB=2EF.∵
2EF=AD+BC,∴
AB=AD+BC.
(2)如果①②④,那么③⑤;如果①③④,那么②⑤;如果①②⑤,那么③④.
21.分析:根据三角形全等的判定,由已知先证∠ACB=∠DCE,再根据SAS可证△ABC≌△DEC,继而可得出结论.
证明:∵
∠1=∠2,∴
∠1+∠ECA=∠2+∠ACE,
即∠ACB=∠DCE.
在△ABC和△DEC中,∵
CA=CD,∠ACB=∠DCE,BC=EC,
∴
△ABC≌△DEC(SAS).∴
DE=AB.
22.分析:(1)连接AP,根据HL证明△APF≌△APE,可得到PE=PF;
(2)利用(1)中的全等,可得出∠FAP=∠EAP,那么点P在∠BAC的平分线上.
证明:(1)如图,连接AP并延长,
∵
PE⊥AB,PF⊥AC,
∴
∠AEP=∠AFP=90°.
在Rt△AEP和Rt△AFP中,AE=AF,AP=AP,
∴
Rt△AEP≌Rt△AFP(HL),
∴
PE=PF.
(2)∵
Rt△AEP≌Rt△AFP,
∴
∠EAP=∠FAP,
∴
AP是∠BAC的角平分线,
故点P在∠BAC的角平分线上.
23.分析:利用ASA证明两个三角形全等即可.
证明:∵
AC∥DF,∴
∠ACB=∠DFE.
在△ABC和△DEF中,
∠A=∠D,AC=DF,∠ACB=∠DFE,
∴
△ABC≌△DEF.
24.分析:灵活运用垂直的定义,注意由垂直可得90°角,由90°角可得垂直,结合平行线的判定和性质,只要证得∠ADC=90°,即可得CD⊥AB.
证明:∵
DG⊥BC,AC⊥BC(已知),
∴
∠DGB=∠ACB=90°(垂直的定义),
∴
DG∥AC(同位角相等,两直线平行).
∴
∠2=∠ACD(两直线平行,内错角相等).
∵
∠1=∠2(已知),∴
∠1=∠ACD(等量代换),
∴
EF∥CD(同位角相等,两直线平行).
∴
∠AEF=∠ADC(两直线平行,同位角相等).
∵
EF⊥AB(已知),∴
∠AEF=90°(垂直的定义),
∴
∠ADC=90°(等量代换).
∴
CD⊥AB(垂直的定义).
第6题图
第10题图
第9题图
第12题图
第16题图
第13题图
第18题图
第21题图
第20题图
第24题图
第23题图
第12题答图
第16题答图
第20题答图
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
