12.2 三角形全等的判定课件(第一课时SSS)
文档属性
| 名称 | 12.2 三角形全等的判定课件(第一课时SSS) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-22 00:00:00 | ||
图片预览







文档简介
课件24张PPT。12.2 全等三角形的判定 0第一课时0(1)能够完全重合的两个三角形叫做全等三角形.(2)全等三角形的性质:
全等三角形的对应边相等,全等三角形的对应角相等.活动10探究一:探索三角形全等的条件创设情境,提出问题两个三角形全等,是否一定需要六个条件呢?
如果只满足六个条件中的一部分,是否也能保证两个三角形全等呢?活动20探究一:探索三角形全等的条件建立模型,探索发现问题:两个三角形满足六个条件中的一个条件,两个三角形全等吗?一个条件有几种情况?一条边或一个角.操作:
(1)让学生画一个一边长为3cm的三角形,画后剪下来看与同桌的三角形能否重合.
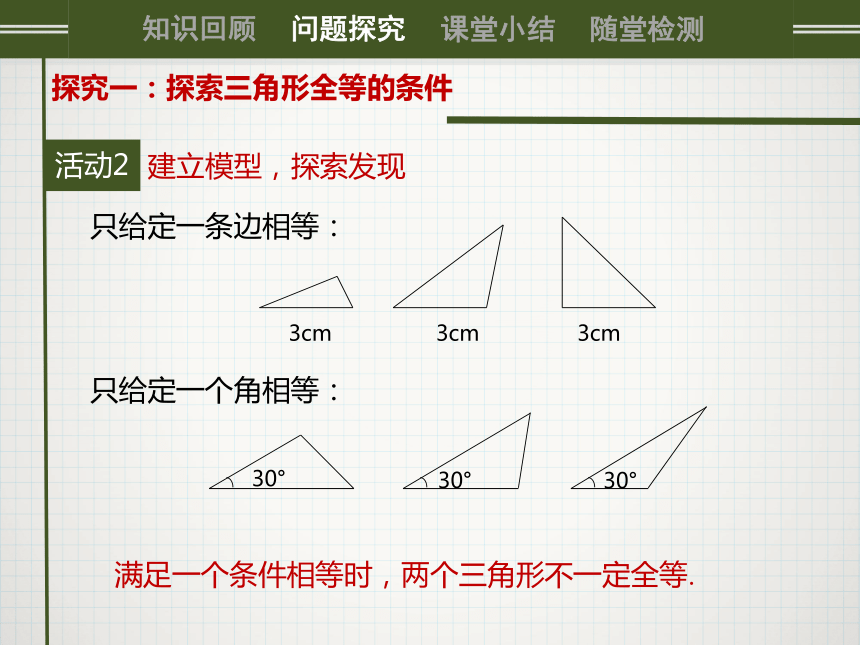
(2)让学生画一个一个角为30°的三角形,画后剪下来看与同桌的三角形能否重合.活动20探究一:探索三角形全等的条件建立模型,探索发现只给定一条边相等:只给定一个角相等:满足一个条件相等时,两个三角形不一定全等.活动30探究一:探索三角形全等的条件问题:两个三角形满足六个条件中的两个条件,两个三角形全等吗?两个条件有几种情况?操作:
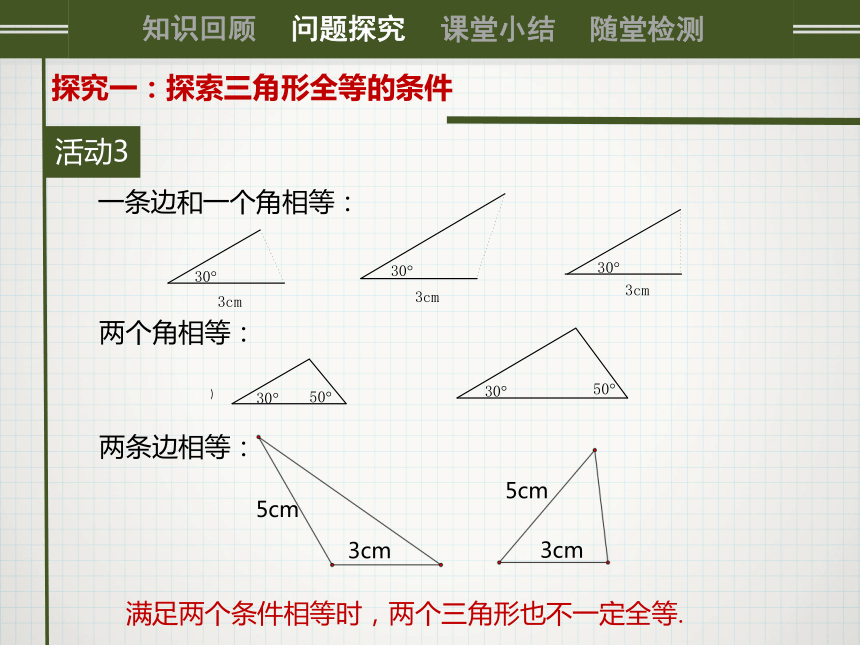
(1)让学生画一个一边长为3cm,一个角为30°的三角形,画好后剪下来看与同桌的三角形能否重合?一条边和一个角相等、两个角相等、两条边相等(2)让学生画一个两个角分别为30°和50°的三角形,画好后剪下来看与同桌的三角形能否重合?(3)让学生画一个两边分别为3cm和5cm的三角形,画好后剪下来看与同桌的三角形能否重合.活动30探究一:探索三角形全等的条件一条边和一个角相等:两个角相等:两条边相等:满足两个条件相等时,两个三角形也不一定全等.活动0探究二:探索三角形全等的判定“边边边”问题:当满足三个条件的两个三角形是否全等,三个条件有几种情况呢?三内角、三条边、两边一内角、两内角一边三个内角对应相等,两个三角形全等吗?△ABC和△ADE都为等边三角形.0探究二:探索三角形全等的判定“边边边”活动操作:
(1)画一个三角形, 三条边长分别为3cm、4cm、5cm.画好后剪下来看与同桌的三角形能否重合.(2)给每个学生发一个△ABC, 根据前面的作法, 作出一个△A′B′C′, 使AB=A′B′、AC=A′C′、BC=B′C′. 将△A′B′C′剪下,观察两个三角形能否重合. 三边分别相等的两个三角形全等.(简写成“边边边”或“SSS”)例10探究三:利用三角形全等的判定“SSS”解决问题 如图,AB=DE,AC=DF,BF=CE.若∠B=40°, ∠D=110°, 则∠DFE=__________ .30°【解题过程】∵BF=CE,∴BC=EF,
又∵AB=DE,AC=DF,∴△ABC≌△DEF,
可得∠B=∠E=40°,
在△DEF中,由三角形的内角和可知,∠DFE=30°.【思路点拨】利用等式的性质, 等式两边同时加上FC, 可得BC=FE, 再得△ABC≌△DEF,最后由全等三角形的性质解决问题.练习0探究三:利用三角形全等的判定“SSS”解决问题 如图,AB=AD,CB=CD,∠B=30° , ∠BAD=48°,则∠ACD=______.126°【解题过程】∵AB=AD,CB=CD,AC=AC,
∴△ABC≌△ADC,
∴∠B=∠D=30°, ∠BAC=∠DAC=24°,
在△ADC中,由三角形的内角和可知,∠ACD=126°.【思路点拨】图中有隐含条件公共边“AC=AC”, 又因为AB=AD, CB=CD, 可得△ABC≌△ADC, 最后由全等三角形的性质解决问题.例20探究三:利用三角形全等的判定“SSS”解决问题解:AD⊥BC,理由如下:
∵D是BC的中点,
∴BD=DC,【解题过程】 △ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架,请问AD⊥BC吗?请说明理由.在△ABD和△ADC中,∴△ABD≌△ACD (SSS).∴ ∠BDA=∠ADC=90° (全等三角形对应角相等),
∴AD⊥BC.【思路点拨】
中点的性质和公共边,注意证全等三角形的规范书写.【数学思想】数形结合思想.证明:∵C是AB的中点,
∴AC=CB.练习0探究三:利用三角形全等的判定“SSS”解决问题如图,C是AB的中点,AD=CE,CD=BE, 求证:CD∥BE.【解题过程】∴ ∠ACD=∠B(全等三角形对应角相等).
∴CD∥BE(同位角相等,两直线平行).【思路点拨】
先证得△ACD≌△CBE, 然后根据全等三角形的对应角相等即可得∠ACD=∠B,最后由平行线的判定可证得CD∥BE.【数学思想】转化思想.在△ACD和△CBE中,∴△ACD≌△CBE (SSS).证明:∵AF=CE,
∴AF-EF=CE-EF.
即AE=CF.例30探究三:利用三角形全等的判定“SSS”解决问题【数学思想】
数形结合思想.【解题过程】∴ ∠DAE=∠BCF(全等三角形对应角相等)
∴AD∥CB(内错角相等,两直线平行)【思路点拨】
先证得△ADE≌△CBF, 然后根据全等三角形的对应角相等即可证得∠DAE=∠BCF,最后由平行线的判定可证得AD∥CB.在△ADE和△CBF中,∴△ADE≌△CBF (SSS).练习0探究三:利用三角形全等的判定“SSS”解决问题 如图, 点B、C、D、E在同一直线上, 已知AB=FC, AD=EF, BC=DE, 请问AD与EF有何关系?并说明理由.【解题过程】∵BC=DE,
∴BC+CD=DE+CD.
即BD=CE.【数学思想】
数形结合思想,分类讨论思想.∴ ∠ADB=∠FEC,AD=EF (全等三角形对应角相等)
∴AD∥EF(同位角相等,两直线平行)在△ABD和△FCE中∴△ABD≌△FCE (SSS).例40探究三:利用三角形全等的判定“SSS”解决问题证明:连接AC,【解题过程】如图, 在四边形ABCD中, AB=AD, CB=CD, 求证:∠B=∠D.∴∠B=∠D.(全等三角形对应角相等)【思路点拨】先连接AC, 由于AB=AD, CB=CD, AC=AC, 利用SSS可证△ABC≌△ADC, 于是∠B=∠D.
要求学生从“形”思维到“质”的思维飞跃, 实现将“文字语言”, “图形语言”转化为“符号语言”.在△ABC和△ADC中∴△ABC≌△ADC(SSS).练习0探究三:利用三角形全等的判定“SSS”解决问题 如图,在 ABC中,∠C=90°,AD=AC,DE=CE.请问ED和AB的位置关系,并说明理由.【解题过程】解:DE⊥AB.
理由如下:连接AE,∴∠ADE=∠C=90°.(全等三角形对应角相等)
∴DE⊥AB【思路点拨】先连接AE, 由于AC=AD, CE=DE, AE=AE, 利用SSS可证△ACE≌△ADE,于是∠ADE=∠C=90°,从而DE⊥AB.在△ACE和△ADE中∴△ACE≌△ADE(SSS).例50探究三:利用三角形全等的判定“SSS”解决问题 如图, 已知∠AOB, 利用直尺和圆规作∠A′O′B′=∠AOB,并说明为什么这样做出来的∠A′O′B′和∠AOB是相等的?【解题过程】作法:
1.以点O为圆心,适当长为半径作弧交OA、OB于点C、D.
2.作任一射线O′A′, 以点O′为圆心,以OC长为半径作弧交O A′于点C′.
3.以点C′为圆心,CD长为半径画弧,与第2步中所画的弧相交于D′.
4.过点D′画射线O′B′,则∠A′O′B′=∠AOB.例50探究三:利用三角形全等的判定“SSS”解决问题 如图, 已知∠AOB, 利用直尺和圆规作∠A′O′B′=∠AOB,并说明为什么这样做出来的∠A′O′B′和∠AOB是相等的?【解题过程】∴ ∠A′O′B′=∠AOB(全等三角形对应角相等).理由:在△DOC和△D′O′C′中∴△DOC≌△D′O′C′(SSS).练习0探究三:利用三角形全等的判定“SSS”解决问题 有一块三角形的厚铁板,根据实际生产需要,工人师傅要把∠MAN平分开.现在他手边只有一把尺子(没有刻度)和一根细绳,你能帮工人师傅想个办法吗?并说明你的根据.【解题过程】用绳子的一定长度在AM,AN边上截取AB=AC,再选取适当长度的绳子,将其对折,得绳子的中点D,把绳子的两端点固定在B,C两点,拉住绳子中点D,向外拉直BD和CD,再在铁板上点出D的位置,作射线AD,则AD平分∠MAN.练习0探究三:利用三角形全等的判定“SSS”解决问题 有一块三角形的厚铁板,根据实际生产需要,工人师傅要把∠MAN平分开.现在他手边只有一把尺子(没有刻度)和一根细绳,你能帮工人师傅想个办法吗?并说明你的根据.【解题过程】知识梳理0(1)三边分别相等的两个三角形全等(可以简写成“边边边”或“SSS”)
(2)利用尺规作一个角等于已知角.重难点突破0(1)培养学生分类讨论思想对问题进行分析.
(2)全等三角形的判定“边边边”的运用及全等三角形的性质.
(3)利用图形语言挖掘隐含条件判定全等,连接线段构造全等三角形.
(4)会用尺规作一个角等于已知角.点击“随堂训练→名师训练”
选择“《三角形全等的判定(1) 》随堂检测 ”0
全等三角形的对应边相等,全等三角形的对应角相等.活动10探究一:探索三角形全等的条件创设情境,提出问题两个三角形全等,是否一定需要六个条件呢?
如果只满足六个条件中的一部分,是否也能保证两个三角形全等呢?活动20探究一:探索三角形全等的条件建立模型,探索发现问题:两个三角形满足六个条件中的一个条件,两个三角形全等吗?一个条件有几种情况?一条边或一个角.操作:
(1)让学生画一个一边长为3cm的三角形,画后剪下来看与同桌的三角形能否重合.
(2)让学生画一个一个角为30°的三角形,画后剪下来看与同桌的三角形能否重合.活动20探究一:探索三角形全等的条件建立模型,探索发现只给定一条边相等:只给定一个角相等:满足一个条件相等时,两个三角形不一定全等.活动30探究一:探索三角形全等的条件问题:两个三角形满足六个条件中的两个条件,两个三角形全等吗?两个条件有几种情况?操作:
(1)让学生画一个一边长为3cm,一个角为30°的三角形,画好后剪下来看与同桌的三角形能否重合?一条边和一个角相等、两个角相等、两条边相等(2)让学生画一个两个角分别为30°和50°的三角形,画好后剪下来看与同桌的三角形能否重合?(3)让学生画一个两边分别为3cm和5cm的三角形,画好后剪下来看与同桌的三角形能否重合.活动30探究一:探索三角形全等的条件一条边和一个角相等:两个角相等:两条边相等:满足两个条件相等时,两个三角形也不一定全等.活动0探究二:探索三角形全等的判定“边边边”问题:当满足三个条件的两个三角形是否全等,三个条件有几种情况呢?三内角、三条边、两边一内角、两内角一边三个内角对应相等,两个三角形全等吗?△ABC和△ADE都为等边三角形.0探究二:探索三角形全等的判定“边边边”活动操作:
(1)画一个三角形, 三条边长分别为3cm、4cm、5cm.画好后剪下来看与同桌的三角形能否重合.(2)给每个学生发一个△ABC, 根据前面的作法, 作出一个△A′B′C′, 使AB=A′B′、AC=A′C′、BC=B′C′. 将△A′B′C′剪下,观察两个三角形能否重合. 三边分别相等的两个三角形全等.(简写成“边边边”或“SSS”)例10探究三:利用三角形全等的判定“SSS”解决问题 如图,AB=DE,AC=DF,BF=CE.若∠B=40°, ∠D=110°, 则∠DFE=__________ .30°【解题过程】∵BF=CE,∴BC=EF,
又∵AB=DE,AC=DF,∴△ABC≌△DEF,
可得∠B=∠E=40°,
在△DEF中,由三角形的内角和可知,∠DFE=30°.【思路点拨】利用等式的性质, 等式两边同时加上FC, 可得BC=FE, 再得△ABC≌△DEF,最后由全等三角形的性质解决问题.练习0探究三:利用三角形全等的判定“SSS”解决问题 如图,AB=AD,CB=CD,∠B=30° , ∠BAD=48°,则∠ACD=______.126°【解题过程】∵AB=AD,CB=CD,AC=AC,
∴△ABC≌△ADC,
∴∠B=∠D=30°, ∠BAC=∠DAC=24°,
在△ADC中,由三角形的内角和可知,∠ACD=126°.【思路点拨】图中有隐含条件公共边“AC=AC”, 又因为AB=AD, CB=CD, 可得△ABC≌△ADC, 最后由全等三角形的性质解决问题.例20探究三:利用三角形全等的判定“SSS”解决问题解:AD⊥BC,理由如下:
∵D是BC的中点,
∴BD=DC,【解题过程】 △ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架,请问AD⊥BC吗?请说明理由.在△ABD和△ADC中,∴△ABD≌△ACD (SSS).∴ ∠BDA=∠ADC=90° (全等三角形对应角相等),
∴AD⊥BC.【思路点拨】
中点的性质和公共边,注意证全等三角形的规范书写.【数学思想】数形结合思想.证明:∵C是AB的中点,
∴AC=CB.练习0探究三:利用三角形全等的判定“SSS”解决问题如图,C是AB的中点,AD=CE,CD=BE, 求证:CD∥BE.【解题过程】∴ ∠ACD=∠B(全等三角形对应角相等).
∴CD∥BE(同位角相等,两直线平行).【思路点拨】
先证得△ACD≌△CBE, 然后根据全等三角形的对应角相等即可得∠ACD=∠B,最后由平行线的判定可证得CD∥BE.【数学思想】转化思想.在△ACD和△CBE中,∴△ACD≌△CBE (SSS).证明:∵AF=CE,
∴AF-EF=CE-EF.
即AE=CF.例30探究三:利用三角形全等的判定“SSS”解决问题【数学思想】
数形结合思想.【解题过程】∴ ∠DAE=∠BCF(全等三角形对应角相等)
∴AD∥CB(内错角相等,两直线平行)【思路点拨】
先证得△ADE≌△CBF, 然后根据全等三角形的对应角相等即可证得∠DAE=∠BCF,最后由平行线的判定可证得AD∥CB.在△ADE和△CBF中,∴△ADE≌△CBF (SSS).练习0探究三:利用三角形全等的判定“SSS”解决问题 如图, 点B、C、D、E在同一直线上, 已知AB=FC, AD=EF, BC=DE, 请问AD与EF有何关系?并说明理由.【解题过程】∵BC=DE,
∴BC+CD=DE+CD.
即BD=CE.【数学思想】
数形结合思想,分类讨论思想.∴ ∠ADB=∠FEC,AD=EF (全等三角形对应角相等)
∴AD∥EF(同位角相等,两直线平行)在△ABD和△FCE中∴△ABD≌△FCE (SSS).例40探究三:利用三角形全等的判定“SSS”解决问题证明:连接AC,【解题过程】如图, 在四边形ABCD中, AB=AD, CB=CD, 求证:∠B=∠D.∴∠B=∠D.(全等三角形对应角相等)【思路点拨】先连接AC, 由于AB=AD, CB=CD, AC=AC, 利用SSS可证△ABC≌△ADC, 于是∠B=∠D.
要求学生从“形”思维到“质”的思维飞跃, 实现将“文字语言”, “图形语言”转化为“符号语言”.在△ABC和△ADC中∴△ABC≌△ADC(SSS).练习0探究三:利用三角形全等的判定“SSS”解决问题 如图,在 ABC中,∠C=90°,AD=AC,DE=CE.请问ED和AB的位置关系,并说明理由.【解题过程】解:DE⊥AB.
理由如下:连接AE,∴∠ADE=∠C=90°.(全等三角形对应角相等)
∴DE⊥AB【思路点拨】先连接AE, 由于AC=AD, CE=DE, AE=AE, 利用SSS可证△ACE≌△ADE,于是∠ADE=∠C=90°,从而DE⊥AB.在△ACE和△ADE中∴△ACE≌△ADE(SSS).例50探究三:利用三角形全等的判定“SSS”解决问题 如图, 已知∠AOB, 利用直尺和圆规作∠A′O′B′=∠AOB,并说明为什么这样做出来的∠A′O′B′和∠AOB是相等的?【解题过程】作法:
1.以点O为圆心,适当长为半径作弧交OA、OB于点C、D.
2.作任一射线O′A′, 以点O′为圆心,以OC长为半径作弧交O A′于点C′.
3.以点C′为圆心,CD长为半径画弧,与第2步中所画的弧相交于D′.
4.过点D′画射线O′B′,则∠A′O′B′=∠AOB.例50探究三:利用三角形全等的判定“SSS”解决问题 如图, 已知∠AOB, 利用直尺和圆规作∠A′O′B′=∠AOB,并说明为什么这样做出来的∠A′O′B′和∠AOB是相等的?【解题过程】∴ ∠A′O′B′=∠AOB(全等三角形对应角相等).理由:在△DOC和△D′O′C′中∴△DOC≌△D′O′C′(SSS).练习0探究三:利用三角形全等的判定“SSS”解决问题 有一块三角形的厚铁板,根据实际生产需要,工人师傅要把∠MAN平分开.现在他手边只有一把尺子(没有刻度)和一根细绳,你能帮工人师傅想个办法吗?并说明你的根据.【解题过程】用绳子的一定长度在AM,AN边上截取AB=AC,再选取适当长度的绳子,将其对折,得绳子的中点D,把绳子的两端点固定在B,C两点,拉住绳子中点D,向外拉直BD和CD,再在铁板上点出D的位置,作射线AD,则AD平分∠MAN.练习0探究三:利用三角形全等的判定“SSS”解决问题 有一块三角形的厚铁板,根据实际生产需要,工人师傅要把∠MAN平分开.现在他手边只有一把尺子(没有刻度)和一根细绳,你能帮工人师傅想个办法吗?并说明你的根据.【解题过程】知识梳理0(1)三边分别相等的两个三角形全等(可以简写成“边边边”或“SSS”)
(2)利用尺规作一个角等于已知角.重难点突破0(1)培养学生分类讨论思想对问题进行分析.
(2)全等三角形的判定“边边边”的运用及全等三角形的性质.
(3)利用图形语言挖掘隐含条件判定全等,连接线段构造全等三角形.
(4)会用尺规作一个角等于已知角.点击“随堂训练→名师训练”
选择“《三角形全等的判定(1) 》随堂检测 ”0
