12.2 三角形全等的判定课件(第二课时SAS)
文档属性
| 名称 | 12.2 三角形全等的判定课件(第二课时SAS) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-22 00:00:00 | ||
图片预览








文档简介
课件30张PPT。12.2 全等三角形的判定 0第二课时0(1)能够完全重合的两个图形叫做全等形,完全重合的两个三角形叫做全等三角形;
(2)全等三角形的对应边相等,对应角相等;
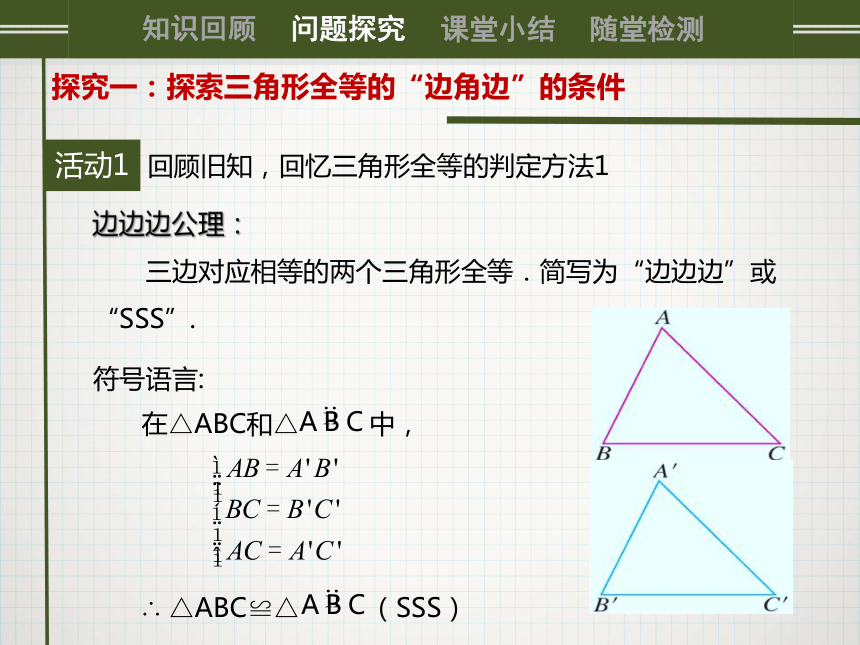
(3)边边边公理:三边分别对应相等的两个三角形全等(简写成“边边边”或“SSS”).活动10回顾旧知,回忆三角形全等的判定方法1边边边公理:
三边对应相等的两个三角形全等.简写为“边边边”或“SSS”.符号语言:探究一:探索三角形全等的“边角边”的条件活动2探究一:探索三角形全等的“边角边”的条件0整合旧知,探究三角形全等的“边角边”的条件(一)猜一猜:把两根木条的一端用螺栓固定在一起.问题1:连接另两端所成的三角形能唯一确定吗?问题2:如果将两条木条之间的夹角(即∠BAC)大小固定,那么△ABC能唯一确定吗?活动20整合旧知,探究三角形全等的“边角边”的条件(二)做一做:探究一:探索三角形全等的“边角边”的条件你能归纳两个三角形全等的判定方法吗?在两个三角形中,
如果有两边和它们的夹角对应相等,
那么这两个三角形全等.(1)用量角器和刻度尺画△ABC, 使AB=2cm, BC=2.5cm, ∠ABC=60°. 然后剪下来,相互比较.
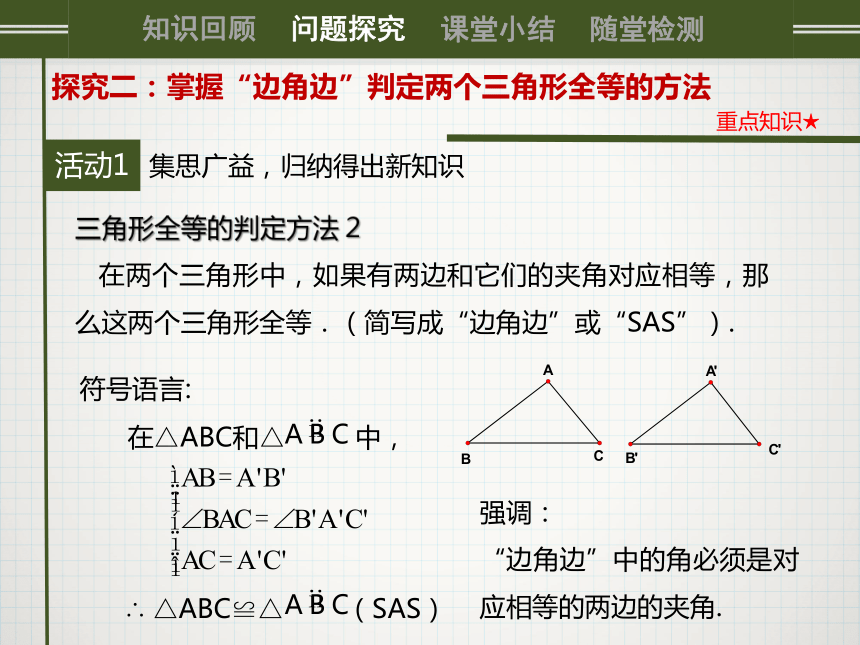
(2)将∠ABC的度数换成20°,再试一试,情况会怎么样?活动1探究二:掌握“边角边”判定两个三角形全等的方法0重点知识★集思广益,归纳得出新知识三角形全等的判定方法 2
在两个三角形中,如果有两边和它们的夹角对应相等,那么这两个三角形全等.(简写成“边角边”或“SAS”).强调:
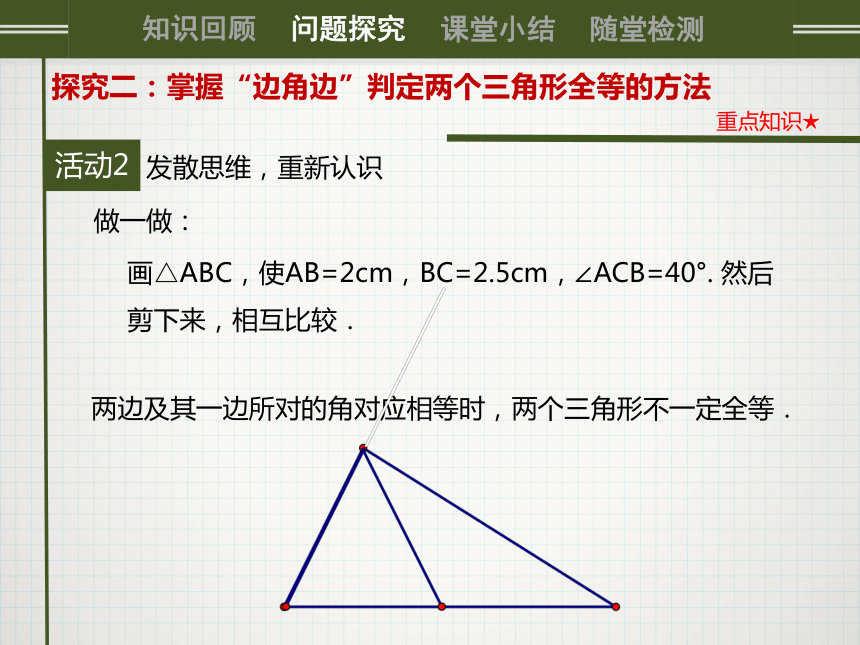
“边角边”中的角必须是对应相等的两边的夹角.符号语言:0发散思维,重新认识活动2探究二:掌握“边角边”判定两个三角形全等的方法重点知识★做一做:画△ABC,使AB=2cm,BC=2.5cm,∠ACB=40°. 然后剪下来,相互比较.两边及其一边所对的角对应相等时,两个三角形不一定全等.0活动2探究二:掌握“边角边”判定两个三角形全等的方法重点知识★强调:
1)格式要求:先指出在哪两个三角形中说明全等;再按判定顺序列出三个条件,并用括号把它们括在一起;写出结论.
2)在应用时,怎样寻找已知条件:已知条件包含两部分,一是已知中给出的,二是图形中隐含的(如公共边,公共角、对顶角、邻补角、外角、平角等). 所以找条件归结成两句话:已知中找,图形中看.
3)平面几何中常要说明角相等和线段相等,其说明常用方法:发散思维,重新认识0活动2探究二:掌握“边角边”判定两个三角形全等的方法重点知识★3)平面几何中常要说明角相等和线段相等,其说明常用方法:发散思维,重新认识证明角相等的方法
对顶角相等;同角(或等角)的余角(或补角)相等;
两直线平行,同位角相等,内错角相等;角平分线定义;等式性质;
全等三角形的对应角相等.
证明线段相等的方法
中点定义;等式性质;
全等三角形的对应边相等.0活动1探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲直接利用“SAS”证明三角形全等【解题过程】【思路点拨】直接应用全等的判定方法“SAS”即可.例1.已知AB=AD,AC=AE,∠BAC=∠DAE,说明△BAC和
△DAE全等的理由.在△BAC和△DAE中,∴ △BAC≌△DAE(SSS)0探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲解:全等,
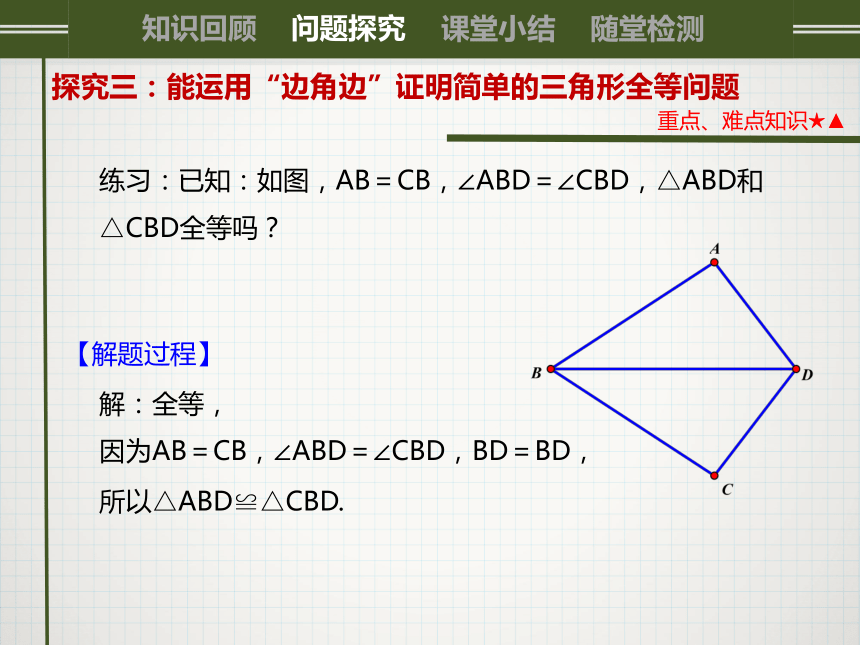
因为AB=CB,∠ABD=∠CBD,BD=BD,练习:已知:如图,AB=CB,∠ABD=∠CBD,△ABD和
△CBD全等吗?【解题过程】所以△ABD≌△CBD.0活动2探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲利用“SAS”及全等三角形的性质证明线段相等【思路点拨】先利用“SAS”证两个三角形全等,再利用全等三角形的对应边相等可得结论.∴ AC=BD.【解题过程】例2.如图, 在△ABC和△ABD中, AC与BD相交于点E, AD=BC,∠DAB=∠CBA. 求证:AC=BD.证明:在△ABC和△ABD中,∴ △ABC≌△BAD(SAS)0探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲【思路点拨】先利用“SAS”证全等,再利用全等性质证两个角相等,再由平行线的判定得平行.∴ ∠A=∠C.∴AB∥CD.【解题过程】练习:如图所示 , AC和BD相交于点O , OA=OC,OB=OD.求证:DC∥AB.证明:在△AOB和△COD中,∴ △AOB≌△COD(SAS)0活动3探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲添加辅助线利用“SAS”解决综合性问题EF=BE+FD0探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲EF=BE+FD仍然成立.
理由:延长FD到点G,使DG=BE,连接AG,
∵∠B+∠ADC=180°,∠ADG+∠ADC=180°,
∴∠B=∠ADG.【解题过程】0探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲∴ AE=AG,∠BAE=∠DAG.∴∠EAF=∠GAF.在△ABE和△ADG中,∴ △ABE≌△ADG(SAS)0探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲又∵FG=DG+DF=BE+DF,
∴EF=BE+FD.∴ EF=FG.【思路点拨】延长FD到点G, 使DG=BE. 连结AG, 证明△ABE≌△ADG,可得AE=AG,再证明△AEF≌△AGF,可得EF=FG,即可解题.在△AEF和△AGF中,∴ △AEF≌△AGF(SAS)0探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲结论:EF=BE+DF.证明思路:证两个全等.0探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲0探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲【解题过程】如图,连接EF,延长AE,BF相交于点C,在四边形AOBC中,∠AOB=30°+90°+20°=140°,又∵OA=OB,
∠OAC+∠OBC=60°+120°=180°,
∴符合探索延伸中的条件,即EF=AE+FB=1.5×(60+80)=210(海里).
答:此时两舰艇之间的距离为210海里.∠EOF=70°=∠AOB,∴结论EF=AE+FB成立.0探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲练习:请阅读,完成证明和填空.
八年级数学兴趣小组在学校的“数学长廊”中兴奋地展示了他们小组探究发现的结果,内容如下:
(1)如图1,正三角形(等边三角形)ABC中,在AB、AC边上分别取点M、N,使BM=AN,连接BN、CM,发现BN=CM,且∠NOC=60°.请证明:∠NOC=60°.【思路点拨】
利用△ABC是正三角形, 可得
∠A=∠ABC=60°, AB=BC.
又因BM=AN,所以△ABN≌△BCM, 可得∠ABN=∠BCM.
所以∠NOC=∠BCM+∠OBC=∠ABN+∠OBC=60°.探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲【解题过程】∴∠ABN=∠BCM.∴∠A=∠ABC=60°,AB=BC.(1)证明:∵△ABC是正三角形,又∵∠ABN+∠OBC=60°,
∴∠BCM+∠OBC=60°.
即∠NOC=60°.在△ABN和△BCM中,∴ △ABN≌△BCM(SAS)0探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲练习:请阅读,完成证明和填空.
八年级数学兴趣小组在学校的“数学长廊”中兴奋地展示了他们小组探究发现的结果,内容如下:
(2)如图2,正方形ABCD中,在AB、BC边上分别取点M、N,使AM=BN,连接AN、DM,那么AN=____,且∠DON=______°.0探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲∴∠DAM=∠ABN=90°,AD=AB.(2)∵四边形ABCD是正方形,又∵∠ADM+∠AMD=90°,
∴∠BAN+∠AMD=90°.
∴∠AOM=90°.
即∠DON=90°.【解题过程】∴ AN=DM, ∠ADM=∠BAN.在△DAM和△ABN中,∴ △DAM≌△ABN(SAS)0探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲练习:请阅读,完成证明和填空.
八年级数学兴趣小组在学校的“数学长廊”中兴奋地展示了他们小组探究发现的结果,内容如下:
(3)如图3, 正五边形ABCDE中, 在AB、BC边上分别取点M、N,使AM=BN,连接AN、EM,那么AN=____,且∠EON=____°.【思路点拨】
(3)同(1)可证得三角形全等, 所以在正五边形中, 有AN=EM, ∠EON= ∠EAB=108°.EM1080探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲练习:请阅读,完成证明和填空.
八年级数学兴趣小组在学校的“数学长廊”中兴奋地展示了他们小组探究发现的结果,内容如下:
(4)在正n边形中,对相邻的三边实施同样的操作过程,也会有类似的结论.请大胆猜测,用一句话概括你的发现:____________知识梳理0(1)三角形全等的判定方法:SAS
(2)判定应用的书写格式.重难点突破0(1)掌握三角形全等的判定方法:SAS;
特别注意:角必须是两条相等的对应边的夹角,边必须是夹相等角的两组对应边.
(2)用“分析法”寻找命题结论也是一种推理论证的方法,即从结论出发逐步递推到题中条件,常以此作为分析寻求推理论证的途径.重难点突破0(3)证明线段、角相等常见的方法:
证明角相等的方法
对顶角相等;同角(或等角)的余角(或补角)相等;两直线平行,同位角相等,内错角相等;角平分线定义;等式性质;全等三角形的对应角相等.
证明线段相等的方法
中点定义;等式性质;全等三角形的对应边相等.点击“随堂训练→名师训练”
选择“《 三角形全等的判定(2)》随堂检测 ”0
(2)全等三角形的对应边相等,对应角相等;
(3)边边边公理:三边分别对应相等的两个三角形全等(简写成“边边边”或“SSS”).活动10回顾旧知,回忆三角形全等的判定方法1边边边公理:
三边对应相等的两个三角形全等.简写为“边边边”或“SSS”.符号语言:探究一:探索三角形全等的“边角边”的条件活动2探究一:探索三角形全等的“边角边”的条件0整合旧知,探究三角形全等的“边角边”的条件(一)猜一猜:把两根木条的一端用螺栓固定在一起.问题1:连接另两端所成的三角形能唯一确定吗?问题2:如果将两条木条之间的夹角(即∠BAC)大小固定,那么△ABC能唯一确定吗?活动20整合旧知,探究三角形全等的“边角边”的条件(二)做一做:探究一:探索三角形全等的“边角边”的条件你能归纳两个三角形全等的判定方法吗?在两个三角形中,
如果有两边和它们的夹角对应相等,
那么这两个三角形全等.(1)用量角器和刻度尺画△ABC, 使AB=2cm, BC=2.5cm, ∠ABC=60°. 然后剪下来,相互比较.
(2)将∠ABC的度数换成20°,再试一试,情况会怎么样?活动1探究二:掌握“边角边”判定两个三角形全等的方法0重点知识★集思广益,归纳得出新知识三角形全等的判定方法 2
在两个三角形中,如果有两边和它们的夹角对应相等,那么这两个三角形全等.(简写成“边角边”或“SAS”).强调:
“边角边”中的角必须是对应相等的两边的夹角.符号语言:0发散思维,重新认识活动2探究二:掌握“边角边”判定两个三角形全等的方法重点知识★做一做:画△ABC,使AB=2cm,BC=2.5cm,∠ACB=40°. 然后剪下来,相互比较.两边及其一边所对的角对应相等时,两个三角形不一定全等.0活动2探究二:掌握“边角边”判定两个三角形全等的方法重点知识★强调:
1)格式要求:先指出在哪两个三角形中说明全等;再按判定顺序列出三个条件,并用括号把它们括在一起;写出结论.
2)在应用时,怎样寻找已知条件:已知条件包含两部分,一是已知中给出的,二是图形中隐含的(如公共边,公共角、对顶角、邻补角、外角、平角等). 所以找条件归结成两句话:已知中找,图形中看.
3)平面几何中常要说明角相等和线段相等,其说明常用方法:发散思维,重新认识0活动2探究二:掌握“边角边”判定两个三角形全等的方法重点知识★3)平面几何中常要说明角相等和线段相等,其说明常用方法:发散思维,重新认识证明角相等的方法
对顶角相等;同角(或等角)的余角(或补角)相等;
两直线平行,同位角相等,内错角相等;角平分线定义;等式性质;
全等三角形的对应角相等.
证明线段相等的方法
中点定义;等式性质;
全等三角形的对应边相等.0活动1探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲直接利用“SAS”证明三角形全等【解题过程】【思路点拨】直接应用全等的判定方法“SAS”即可.例1.已知AB=AD,AC=AE,∠BAC=∠DAE,说明△BAC和
△DAE全等的理由.在△BAC和△DAE中,∴ △BAC≌△DAE(SSS)0探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲解:全等,
因为AB=CB,∠ABD=∠CBD,BD=BD,练习:已知:如图,AB=CB,∠ABD=∠CBD,△ABD和
△CBD全等吗?【解题过程】所以△ABD≌△CBD.0活动2探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲利用“SAS”及全等三角形的性质证明线段相等【思路点拨】先利用“SAS”证两个三角形全等,再利用全等三角形的对应边相等可得结论.∴ AC=BD.【解题过程】例2.如图, 在△ABC和△ABD中, AC与BD相交于点E, AD=BC,∠DAB=∠CBA. 求证:AC=BD.证明:在△ABC和△ABD中,∴ △ABC≌△BAD(SAS)0探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲【思路点拨】先利用“SAS”证全等,再利用全等性质证两个角相等,再由平行线的判定得平行.∴ ∠A=∠C.∴AB∥CD.【解题过程】练习:如图所示 , AC和BD相交于点O , OA=OC,OB=OD.求证:DC∥AB.证明:在△AOB和△COD中,∴ △AOB≌△COD(SAS)0活动3探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲添加辅助线利用“SAS”解决综合性问题EF=BE+FD0探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲EF=BE+FD仍然成立.
理由:延长FD到点G,使DG=BE,连接AG,
∵∠B+∠ADC=180°,∠ADG+∠ADC=180°,
∴∠B=∠ADG.【解题过程】0探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲∴ AE=AG,∠BAE=∠DAG.∴∠EAF=∠GAF.在△ABE和△ADG中,∴ △ABE≌△ADG(SAS)0探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲又∵FG=DG+DF=BE+DF,
∴EF=BE+FD.∴ EF=FG.【思路点拨】延长FD到点G, 使DG=BE. 连结AG, 证明△ABE≌△ADG,可得AE=AG,再证明△AEF≌△AGF,可得EF=FG,即可解题.在△AEF和△AGF中,∴ △AEF≌△AGF(SAS)0探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲结论:EF=BE+DF.证明思路:证两个全等.0探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲0探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲【解题过程】如图,连接EF,延长AE,BF相交于点C,在四边形AOBC中,∠AOB=30°+90°+20°=140°,又∵OA=OB,
∠OAC+∠OBC=60°+120°=180°,
∴符合探索延伸中的条件,即EF=AE+FB=1.5×(60+80)=210(海里).
答:此时两舰艇之间的距离为210海里.∠EOF=70°=∠AOB,∴结论EF=AE+FB成立.0探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲练习:请阅读,完成证明和填空.
八年级数学兴趣小组在学校的“数学长廊”中兴奋地展示了他们小组探究发现的结果,内容如下:
(1)如图1,正三角形(等边三角形)ABC中,在AB、AC边上分别取点M、N,使BM=AN,连接BN、CM,发现BN=CM,且∠NOC=60°.请证明:∠NOC=60°.【思路点拨】
利用△ABC是正三角形, 可得
∠A=∠ABC=60°, AB=BC.
又因BM=AN,所以△ABN≌△BCM, 可得∠ABN=∠BCM.
所以∠NOC=∠BCM+∠OBC=∠ABN+∠OBC=60°.探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲【解题过程】∴∠ABN=∠BCM.∴∠A=∠ABC=60°,AB=BC.(1)证明:∵△ABC是正三角形,又∵∠ABN+∠OBC=60°,
∴∠BCM+∠OBC=60°.
即∠NOC=60°.在△ABN和△BCM中,∴ △ABN≌△BCM(SAS)0探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲练习:请阅读,完成证明和填空.
八年级数学兴趣小组在学校的“数学长廊”中兴奋地展示了他们小组探究发现的结果,内容如下:
(2)如图2,正方形ABCD中,在AB、BC边上分别取点M、N,使AM=BN,连接AN、DM,那么AN=____,且∠DON=______°.0探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲∴∠DAM=∠ABN=90°,AD=AB.(2)∵四边形ABCD是正方形,又∵∠ADM+∠AMD=90°,
∴∠BAN+∠AMD=90°.
∴∠AOM=90°.
即∠DON=90°.【解题过程】∴ AN=DM, ∠ADM=∠BAN.在△DAM和△ABN中,∴ △DAM≌△ABN(SAS)0探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲练习:请阅读,完成证明和填空.
八年级数学兴趣小组在学校的“数学长廊”中兴奋地展示了他们小组探究发现的结果,内容如下:
(3)如图3, 正五边形ABCDE中, 在AB、BC边上分别取点M、N,使AM=BN,连接AN、EM,那么AN=____,且∠EON=____°.【思路点拨】
(3)同(1)可证得三角形全等, 所以在正五边形中, 有AN=EM, ∠EON= ∠EAB=108°.EM1080探究三:能运用“边角边”证明简单的三角形全等问题重点、难点知识★▲练习:请阅读,完成证明和填空.
八年级数学兴趣小组在学校的“数学长廊”中兴奋地展示了他们小组探究发现的结果,内容如下:
(4)在正n边形中,对相邻的三边实施同样的操作过程,也会有类似的结论.请大胆猜测,用一句话概括你的发现:____________知识梳理0(1)三角形全等的判定方法:SAS
(2)判定应用的书写格式.重难点突破0(1)掌握三角形全等的判定方法:SAS;
特别注意:角必须是两条相等的对应边的夹角,边必须是夹相等角的两组对应边.
(2)用“分析法”寻找命题结论也是一种推理论证的方法,即从结论出发逐步递推到题中条件,常以此作为分析寻求推理论证的途径.重难点突破0(3)证明线段、角相等常见的方法:
证明角相等的方法
对顶角相等;同角(或等角)的余角(或补角)相等;两直线平行,同位角相等,内错角相等;角平分线定义;等式性质;全等三角形的对应角相等.
证明线段相等的方法
中点定义;等式性质;全等三角形的对应边相等.点击“随堂训练→名师训练”
选择“《 三角形全等的判定(2)》随堂检测 ”0
