人教版九年级数学下册第二十八章 《锐角三角函数复习》 课件
文档属性
| 名称 | 人教版九年级数学下册第二十八章 《锐角三角函数复习》 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 944.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-23 11:13:49 | ||
图片预览





文档简介
课件22张PPT。 锐角三角函数复习学习目标学习目标1. 巩固三角函数的概念,巩固用直角三角形边之比来表示某个锐角的三角函数.
2. 熟记30°,45°, 60°角的三角函数值.会计算含有特殊角的三角函数的值,会由一个特殊锐角的三角函数值,求出它的对应的角度.
3.掌握直角三角形的边角关系,会运用勾股定理,直角三角形的两锐角互余及锐角三角函数解直角三角形.
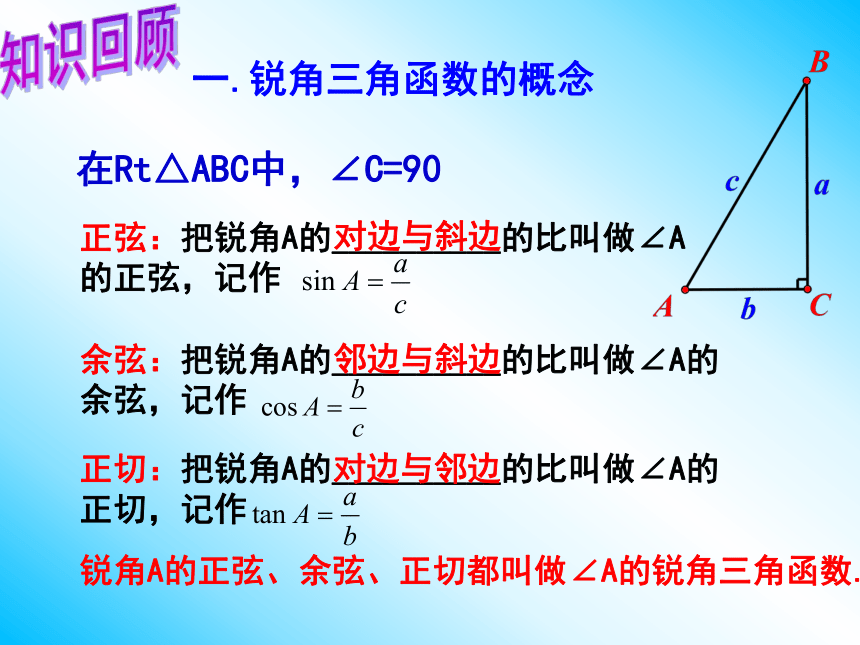
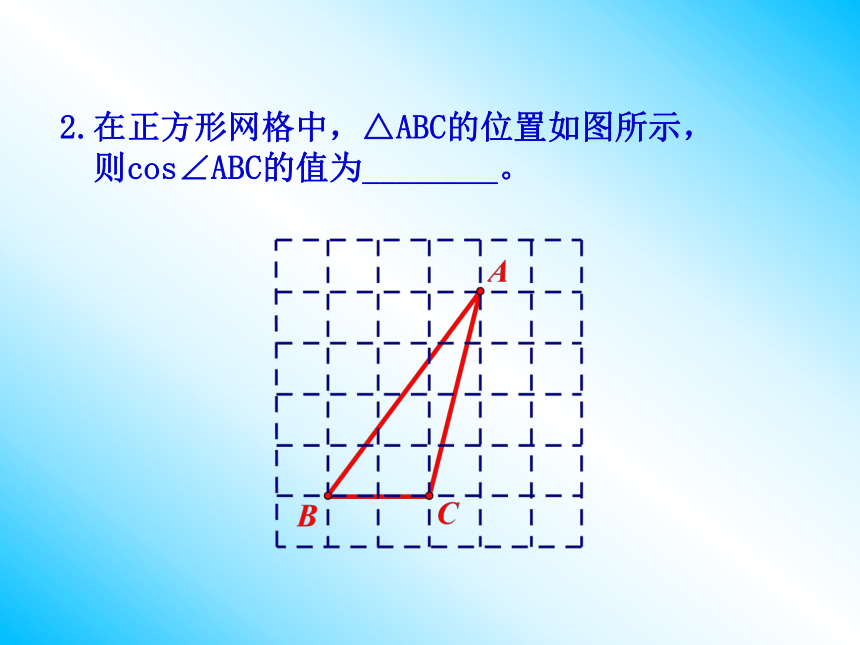
4.会用解直角三角形的有关知识解决简单的实际问题. 知识回顾知识回顾1一.锐角三角函数的概念正弦:把锐角A的__________的比叫做∠A的正弦,记作 余弦:把锐角A的__________的比叫做∠A的余弦,记作 正切:把锐角A的__________的比叫做∠A的正切,记作 锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.对边与斜边邻边与斜边对边与邻边在Rt△ABC中,∠C=901.如图,在Rt△ABC中,∠C=90,AB=5,AC=3,求sinA,cosA及tanA。2.在正方形网格中,△ABC的位置如图所示,
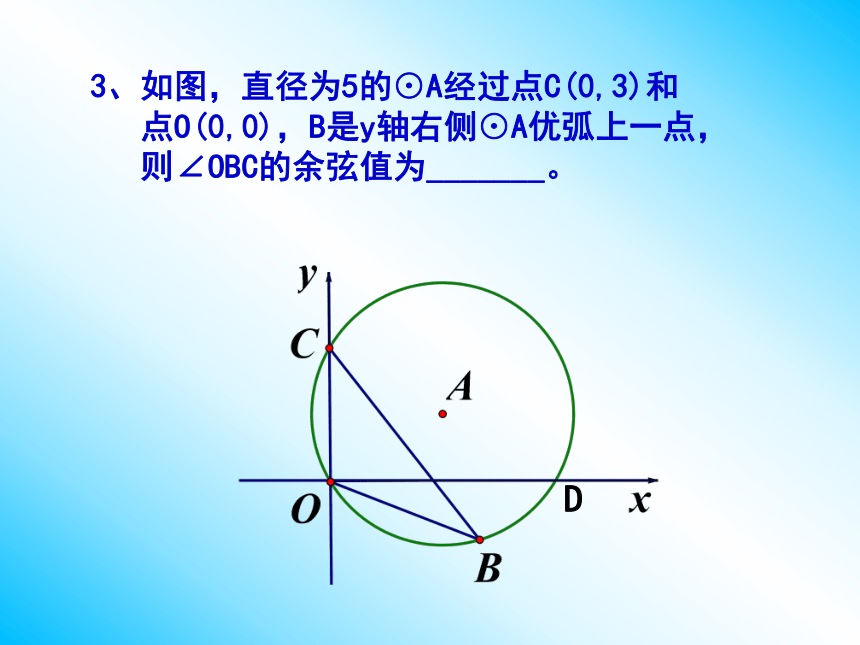
则cos∠ABC的值为________。3、如图,直径为5的⊙A经过点C(0,3)和
点O(0,0),B是y轴右侧⊙A优弧上一点,
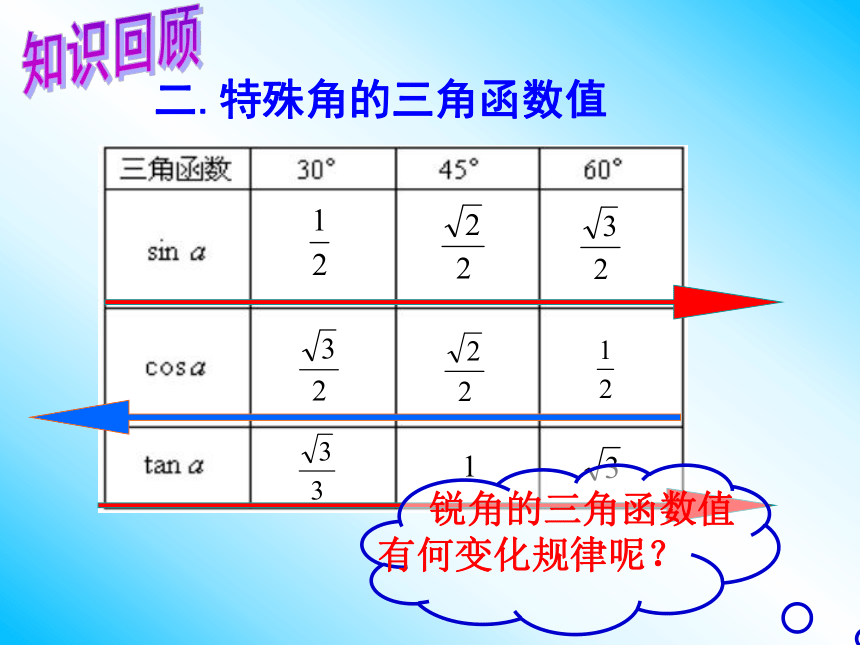
则∠OBC的余弦值为_______。D知识回顾知识回顾2二.特殊角的三角函数值 锐角的三角函数值有何变化规律呢?三角函数的增减性:正切值和正弦值都随着锐角度数的增大而_____;
余弦值随着锐角度数的增大而_____.增大减小当A为锐角时,0<sinA<1,0<cosA<1,tanA>0.(1)sin250____sin430
(2)cos70____cos80
(3)tan480____tan400一.比较大小☆ 应用练习二.已知角,求值☆ 应用练习三.已知值,求角知识回顾知识回顾3三.解直角三角形在直角三角形中,除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形.1.什么叫解直角三角形?2.直角三角形中的边角关系:∠A十∠B=90° 归纳:只要知道其中的2个元素(至少有一个是____),就可以求出其余3个未知元素. (1)三边关系:(勾股定理)(2)两锐角的关系:(3)边角的关系:边小试身手1.在Rt △ ABC中,∠C=90°,∠ A=30°,b=5,
求a、c的大小.四、解直角三角形的应用(1)将实际问题抽象为数学问题;(画出图形、转化为直角三角形问题)(2)选择适当的三角函数解直角三角形;(3)得到数学问题的答案。(4)得到实际问题的答案。如图,在一笔直的海岸线上有A,B两个观测站,A在B的正西方向,AB=2km,从A测得船C在北偏东60°的方向,从B测得船C在北偏西45°的方向.求船C离海岸线的距离.A B C 2km 60° 45° 根据图中所给的数据,求避雷针
CD的长。 某人在A处测得建筑物的仰角∠BAC为300 ,沿AC方向行20m至D处,测得仰角∠BDC 为450,求此建筑物的高度BC.ACB____________________D 有一段防洪大堤,横截面为梯形ABCD,AB∥CD,斜坡AD的坡度 为1:1.2,斜坡BC的坡度 为1:0.8,大坝底宽AB为10米,坝高2米,求坝顶宽。i1=1:1.2i2=1:0.810米ABCD如图,在某海域内有A、C两个港口,港口C在港口A北偏东60°方向上.一艘船以每小时36海里的速度沿北偏东30°的方向驶离A港口,3小时后到达B点位置,在B处测得港口C在B处的南偏东75°方向上,求B处离港口C有多少海里?(结果保留根号)ABC2.30°、45°、60°特殊角的三角函数值⑶解直角三角形在实际问题中的应用小结作业教材 P68—69 习题知识回顾知识回顾41.仰角和俯角在进行测量时,
从下向上看,视线与水平线的夹角叫做____;
从上往下看,视线与水平线的夹角叫做____。
铅直线水平线视线视线仰角俯角仰角俯角坡度:坡面的铅直高度h和水平距离l的比叫做坡度,用字母i表示,即:2.坡角、坡度坡角:坡面与水平面的夹角叫做坡角,用字母α表示.hl知识回顾
2. 熟记30°,45°, 60°角的三角函数值.会计算含有特殊角的三角函数的值,会由一个特殊锐角的三角函数值,求出它的对应的角度.
3.掌握直角三角形的边角关系,会运用勾股定理,直角三角形的两锐角互余及锐角三角函数解直角三角形.
4.会用解直角三角形的有关知识解决简单的实际问题. 知识回顾知识回顾1一.锐角三角函数的概念正弦:把锐角A的__________的比叫做∠A的正弦,记作 余弦:把锐角A的__________的比叫做∠A的余弦,记作 正切:把锐角A的__________的比叫做∠A的正切,记作 锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.对边与斜边邻边与斜边对边与邻边在Rt△ABC中,∠C=901.如图,在Rt△ABC中,∠C=90,AB=5,AC=3,求sinA,cosA及tanA。2.在正方形网格中,△ABC的位置如图所示,
则cos∠ABC的值为________。3、如图,直径为5的⊙A经过点C(0,3)和
点O(0,0),B是y轴右侧⊙A优弧上一点,
则∠OBC的余弦值为_______。D知识回顾知识回顾2二.特殊角的三角函数值 锐角的三角函数值有何变化规律呢?三角函数的增减性:正切值和正弦值都随着锐角度数的增大而_____;
余弦值随着锐角度数的增大而_____.增大减小当A为锐角时,0<sinA<1,0<cosA<1,tanA>0.(1)sin250____sin430
(2)cos70____cos80
(3)tan480____tan400一.比较大小☆ 应用练习二.已知角,求值☆ 应用练习三.已知值,求角知识回顾知识回顾3三.解直角三角形在直角三角形中,除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形.1.什么叫解直角三角形?2.直角三角形中的边角关系:∠A十∠B=90° 归纳:只要知道其中的2个元素(至少有一个是____),就可以求出其余3个未知元素. (1)三边关系:(勾股定理)(2)两锐角的关系:(3)边角的关系:边小试身手1.在Rt △ ABC中,∠C=90°,∠ A=30°,b=5,
求a、c的大小.四、解直角三角形的应用(1)将实际问题抽象为数学问题;(画出图形、转化为直角三角形问题)(2)选择适当的三角函数解直角三角形;(3)得到数学问题的答案。(4)得到实际问题的答案。如图,在一笔直的海岸线上有A,B两个观测站,A在B的正西方向,AB=2km,从A测得船C在北偏东60°的方向,从B测得船C在北偏西45°的方向.求船C离海岸线的距离.A B C 2km 60° 45° 根据图中所给的数据,求避雷针
CD的长。 某人在A处测得建筑物的仰角∠BAC为300 ,沿AC方向行20m至D处,测得仰角∠BDC 为450,求此建筑物的高度BC.ACB____________________D 有一段防洪大堤,横截面为梯形ABCD,AB∥CD,斜坡AD的坡度 为1:1.2,斜坡BC的坡度 为1:0.8,大坝底宽AB为10米,坝高2米,求坝顶宽。i1=1:1.2i2=1:0.810米ABCD如图,在某海域内有A、C两个港口,港口C在港口A北偏东60°方向上.一艘船以每小时36海里的速度沿北偏东30°的方向驶离A港口,3小时后到达B点位置,在B处测得港口C在B处的南偏东75°方向上,求B处离港口C有多少海里?(结果保留根号)ABC2.30°、45°、60°特殊角的三角函数值⑶解直角三角形在实际问题中的应用小结作业教材 P68—69 习题知识回顾知识回顾41.仰角和俯角在进行测量时,
从下向上看,视线与水平线的夹角叫做____;
从上往下看,视线与水平线的夹角叫做____。
铅直线水平线视线视线仰角俯角仰角俯角坡度:坡面的铅直高度h和水平距离l的比叫做坡度,用字母i表示,即:2.坡角、坡度坡角:坡面与水平面的夹角叫做坡角,用字母α表示.hl知识回顾
