数学二年级下册人教版第五单元混合运算 精编教案
文档属性
| 名称 | 数学二年级下册人教版第五单元混合运算 精编教案 |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-23 08:26:38 | ||
图片预览




文档简介
在学习混合运算之前,学生已经接触过100以内的两步连加、连减计算及变相的两步混合计算,为本单元系统地学习混合运算奠定了基础。本单元教学内容主要包括:没有括号的同级混合运算,没有括号的两级混合运算,有括号的混合运算以及运用混合运算解决实际问题。这是学生系统学习运算顺序的重要阶段,是今后练习计算、提高计算能力的关键。
由于学生之前已经或多或少的接触过混合运算,只是缺乏对混合运算顺序的归纳总结,所以本单元的学习,对于学生来说没有太大难度,关键就是掌握不同情况下混合运算的计算顺序,并能熟练地进行计算。
1.使学生掌握几种不同情况下的混合运算的计算顺序,并能正确地进行计算。
2.能结合具体情境理解混合运算的计算顺序,并能熟练运用混合运算解决简单的实际问题
1.通过多种多样的练习,使学生掌握混合运算的计算顺序,提高学生的计算能力和水平。
2.结合具体的情境分析,帮助学生理解并掌握混合运算的计算顺序,为今后计算能力的提高做准备。
1 混合运算顺序
1课时
2 练习十一
1课时
3 解决问题
1课时
4 练习十二
1课时
5 整理和复习 练习十三
1课时
混合运算顺序。(教材第47~49页)
1.结合具体练习,使学生掌握混合运算的计算顺序。
2.通过多种多样的练习,提高学生的计算能力。
重点:使学生掌握混合运算的计算顺序。
难点:提高学生的计算能力。
课件。
师:同学们,我们以前学过100以内的两步连加、连减计算,你们还记得计算顺序是怎样的吗
生:100以内的两步连加、连减计算,是按从左往右的顺序计算的。
【设计意图:“温故而知新”,引导学生回忆100以内的两步连加、连减计算的顺序,为混合运算顺序的教学做准备】
1.教学例1。
师:你还记得53-24+38是按怎样的运算顺序计算的吗
生:按从左往右的顺序,先算减法再算加法。
师:好。看谁算得又对又快。
学生独立完成后,组织学生交流汇报。
师:我们以前学过的加、减、乘、除这四种运算,其实是两级不同的运算,加法和减法是同一级的运算,乘法和除法是同一级的运算。在没有括号的算式里,只有加减法或只有乘除法,都要按从左往右的顺序计算。也可以说在没有括号的算式里,只有同级运算,都要按从左往右的顺序计算。
师:计算53-24+38,为了便于看出这个综合算式的运算顺序,我们采用脱式计算,写出每次运算的结果。(边讲解边板书)
师:现在请大家像老师这样把综合算式15÷3×5的计算过程写下来。
学生独立完成计算,教师巡视了解情况,然后组织学生交流汇报。
师:接下来我们进行一场比赛,用刚才的方法计算下面各题,看谁算得又对又快。(课件出示:教材第47页“做一做”)
学生尝试独立完成练习,教师巡视,指导个别学习有困难的学生。最后组织交流汇报,对完全正确的同学给予表扬鼓励。
2.教学例2。
师:请看题目,你发现了什么 (课件出示:教材第48页例2)
生1:在跷跷板乐园里,有3组小朋友正在玩跷跷板,每组有4人。
生2:还有7位小朋友在周围观看,问跷跷板乐园一共有多少人。
师:想一想,先算什么,再算什么 怎样列式计算呢
生1:我先算跷跷板上有多少人,4×3=12(人);再算一共有多少人,12+7=19(人)。
生2:我也是这么算的,不过我列的是综合算式,4×3+7=19(人)。
生3:在我列的算式里,7+(4×3)=19(人),因为要先求4×3,就用小括号了。
师:同学们的想法都很棒!其中7+(4×3)可以写成7+4×3,因为在没有括号的算式里,如果既有乘法(或除法),又有加减法,要先算乘法(或除法),后算加减法。也可以说在没有括号的算式里,要先乘除后加减。
师:现在请同学们把下面各题第一步要先算什么圈出来。(课件出示:教材第48页“做一做”)
(教师逐一出示,学生逐一回答,教师及时做出评价,以鼓励为主)
师:现在同学们运用这个规则完成例2的计算,好吗
学生尝试独立完成计算,教师巡视了解情况。
组织学生交流汇报,重点说明运算顺序。教师结合反馈情况,进行强调讲解。
3.教学例3。
师:刚才我们说的两种情况也可以归纳为一种情况,它们都是没有括号的算式,如果在有括号的算式里,运算顺序又是怎样的 (课件出示:教材第49页最上面一句话)
学生齐读:算式里有括号的,要先算括号里面的。
师:运用这个规则,你能完成下面的习题吗 (课件出示:教材第49页例3)
学生尝试独立完成,教师巡视了解情况。
组织学生交流汇报,重点说明运算顺序。
【设计意图:层层深入,由扶到放,逐步引导学生掌握混合运算的顺序。在告诉学生运算法则的情况下,放手让学生尝试独立计算,既可以有效地锻炼学生的计算能力,又可以使学生把所学的知识点掌握牢固】
师:同学们,通过今天的学习,你们学会了什么
(在没有括号的算式里,如果只有同级运算,就按从左往右的顺序计算;如果含有两级运算,要先算乘除后算加减。算式里有括号的,要先算括号里面的)
【设计意图:课末总结能有效地帮助学生回顾本节课所学知识,使之系统化、条理化,提高课堂教学效率】
1.在学习过程中,学生不断地获得新的知识,不断产生惊喜。要经常评价学生、鼓励学生,给学生以自信。在教学过程中要耐心倾听学生的发言,热情鼓励学生,让学生感受到心与心、情与情的真诚交流。
2.以小组合作的形式组织教学,体现了“自主探索、合作交流、实践创新”的数学学习方式,培养了学生互相合作交流的意识,让学生在共同讨论中完成学习任务。
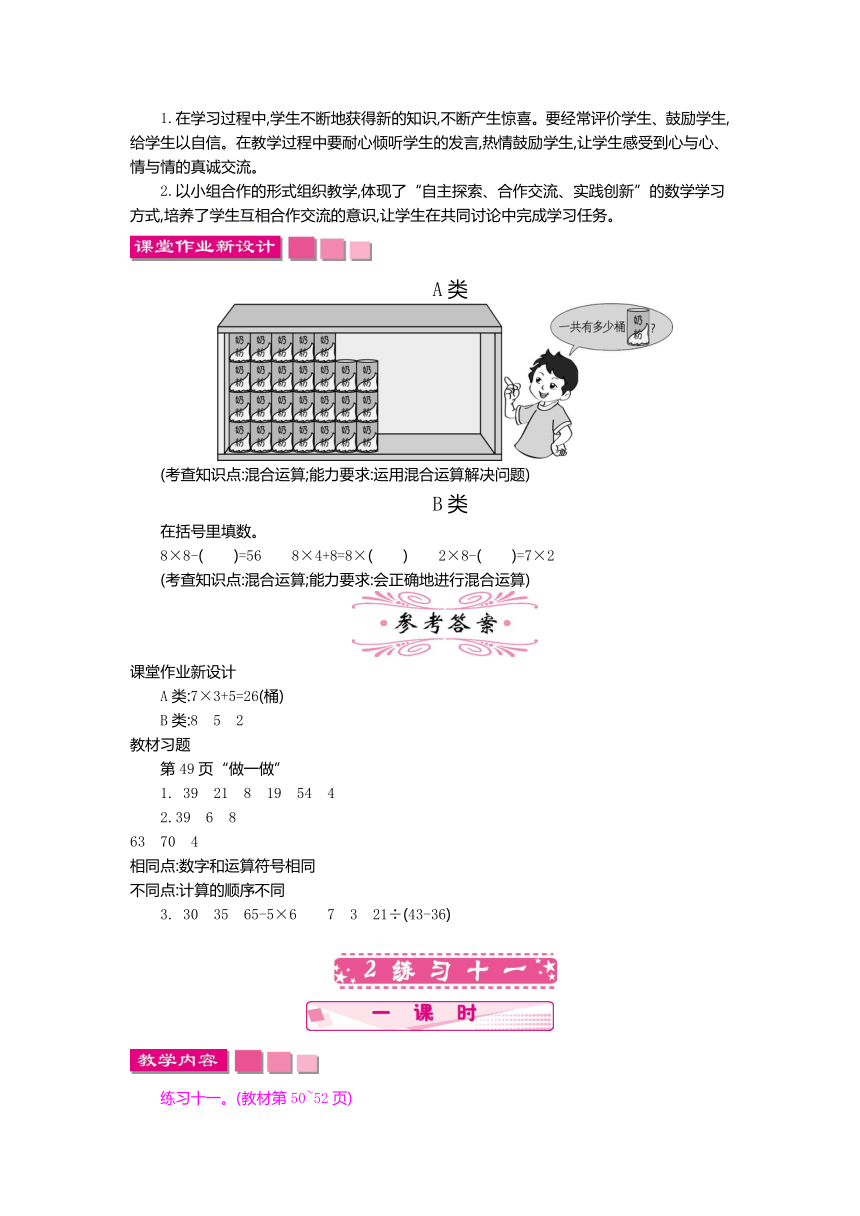
A类
(考查知识点:混合运算;能力要求:运用混合运算解决问题)
B类
在括号里填数。
8×8-( )=56 8×4+8=8×( ) 2×8-( )=7×2
(考查知识点:混合运算;能力要求:会正确地进行混合运算)
课堂作业新设计
A类:7×3+5=26(桶)
B类:8 5 2
教材习题
第49页“做一做”
1.
39 21 8 19 54 4
2.39 6 8
63 70 4
相同点:数字和运算符号相同
不同点:计算的顺序不同
3.
30 35 65-5×6 7 3 21÷(43-36)
练习十一。(教材第50~52页)
1.使学生进一步掌握混合运算的计算顺序。
2.通过巩固练习,进一步提高学生的计算能力。
重点:进一步掌握混合运算的计算顺序。
难点:进一步提高学生的计算能力。
课件。
师:同学们,通过学习混合运算顺序,你们有什么收获
学生可能会说:
·我知道了在没有括号的算式里,如果只有加减法或只有乘除法,都要按从左往右的顺序计算。
·我知道了在没有括号的算式里,如果既有乘除法,又有加减法,要先算乘除法,后算加减法。
·我知道了算式里有括号的,要先算括号里面的。
……
师:仅仅知道这些运算顺序是不够的,只有多多练习,我们才能熟练地进行混合计算。
师:仔细观察,比较上下两题的运算顺序和计算结果,说一说你发现了什么 (课件出示:教材第51页第8题)
学生尝试独立解答,然后在小组里交流,教师巡视了解情况。
组织交流汇报:
·第一组算式的区别在于上面的一题没有括号,要先算除法再算加法,这样计算的结果是21;下面的一题有括号,要先算括号里面的加法,再算括号外面的除法,这样计算的结果是5。
·第二组算式的区别同样是括号,上面的一题没有括号,要先算乘法再算减法,这样计算的结果是29;下面的一题有括号,要先算括号里面的减法,再算括号外面的乘法,这样计算的结果是20。
·我觉得这两组算式的结果之所以会不相同,跟括号有关。
·我认为是括号改变了运算顺序,所以结果才会不同。
……
(给学生足够的时间和机会发表自己的见解,正确的要给予鼓励)
师:括号的确有改变运算顺序的作用,所以在计算的时候一定要细心,看清有没有括号,弄明白先算什么再算什么,明确了运算顺序才能把题做对。
【设计意图:在具体的对比练习中,使学生认识到有没有括号很重要,提醒学生认真细心,培养学生良好的学习习惯】
师:同学们,通过今天的学习,你们收获了什么呢
1.通过这节课的学习,学生已经掌握了混合运算的计算顺序,但是计算的准确率及速度还要在进一步的练习中逐渐提高。
2.结合已有的知识经验进行教学,加上教师适时的引导启发,学生学习起来事半功倍。在学习过程中,放手让学生尝试自己解决问题,培养学生的口头表达能力和合作意识。同时在计算过程中,教师要引导学生反思,培养学生总结归纳的能力。
A类
东东去商店买了一辆小汽车,给售货员阿姨4张5元钱,售货员阿姨又找给他2元,那么这辆小汽车多少钱
(考查知识点:混合运算;能力要求:能结合实际情况,运用混合运算解决问题)
B类
小明从第1棵树跑到第5棵树,一共跑了多少米
(考查知识点:混合运算;能力要求:能结合实际情况,运用混合运算解决问题)
课堂作业新设计
A类:4×5-2=18(元)
B类:5×(5-1)=20(米)
教材习题
第50~52页“练习十一”
1.
38 58 17 9 3 54
2.8 22 3 15
15
29
5
25
21
35
7
35
23
37
9
45
3. 34-17+3 第二个计算对 18÷3×3
=17+3 =6×3
=20
=18
4.
43 17 11 19 4 59
5.
= < < <
6.
9 6 81÷9-3=6 56 88 32+7×8=88
7.
25 54 20 60 7 4
8.
21 29 5 20
9.42+14-35=21 7×9-28=35 62-(15-3)=50 50-36÷6=44
(6+6)÷3=4 (54-22)÷8=4 36÷(16÷4)=9 14÷(83-76)=2
10.
13 13 42 13 13 42
11.
82 8 8 26 9 53
12.
32 25+8×4=57(元)
13.
35-3=32(元) 32÷8=4(个)
14.
(1)12+36÷4=21 (2)(12+8)÷5=4
解决问题。(教材第53、第54页)
1.在具体情境中,运用混合运算解决简单的实际问题,进一步促使学生理解混合运算的计算顺序。
2.培养学生运用所学知识解决生活中简单的实际问题的能力。
重点:运用混合运算解决简单的实际问题。
难点:结合具体问题,理解混合运算计算顺序的合理性。
课件。
师:同学们,在我们的日常生活中有许多问题不是靠一步计算就能解决的,所以混合运算在我们日常生活中的应用很广泛。
1.教学例4。
师:看看面包师傅遇到了什么问题 你知道了什么 (课件出示:教材第53页例4)
生:知道一共要烤90个面包,已经烤了36个,剩下的每次烤9个,还需要烤多少次
师:你有办法帮面包师傅解决问题吗
生1:我们可以先计算还剩多少个没烤,90-36=54(个),把剩下的54个,每次烤9个,54里面有几个9就是需要烤多少次,54÷9=6(次)。
生2:我可以把两个算式合并成一个综合算式:(90-36)÷9。
师:用综合算式计算的时候为什么要加小括号呢
生:因为我们要先计算还剩下多少个没有烤,就必须要先算减法,那就要加小括号,否则就要先算除法了。
师:说得很有道理,老师可以教大家画图来帮助我们分析理解题意,请看:
(边画图边讲解分析)
师:该怎样思考用多个步骤解决的问题呢
生:如果一个问题需要多个步骤才能解决,要想好先算什么再算什么,才能正确解答。
2.教学“做一做”。
师:你能自己解答下面的问题吗 可以在小组里交流讨论。(课件出示:教材第54页“做一做”)
学生尝试自己解答,教师巡视了解情况。
师:谁愿意把自己的想法和结果告诉大家
学生可能会说:
·可以先计算第一组买9个花多少钱,9×3=27(元);再计算第二组买6个花多少钱,6×3=18(元),这样就可以算出第一组比第二组多花多少钱,27-18=9(元)。列成综合算式:9×3-6×3=9(元)。
·可以先计算第一组比第二组多买几个,9-6=3(个);每个3元,就是3×3=9(元)。列成综合算式:(9-6)×3=9(元)。
(如果以上两种解法学生没有答出来,教师可以介绍给学生,但是第一种解答方法不要求所有学生掌握)
【设计意图:把抽象的运算顺序与具体情境相结合,能使学生更好地掌握混合运算的顺序,突破教学重难点】
师:同学们,今天的内容你们学会了吗
在较好地掌握混合运算顺序的基础上,进行解决实际问题的教学,既能帮助学生更好地掌握运算顺序,又能使学生切身体会到数学的应用价值。但是在具体的计算过程中,因粗心等原因会导致结果不正确,因此要培养学生养成良好的学习习惯。
A类
小朋友举行队列操比赛,原来是每行9人,站了4行;老师觉得队列有点长,就想改为6行,现在每行站几个小朋友
(考查知识点:混合运算;能力要求:运用混合运算解决问题)
B类
找规律填空。
(考查知识点:混合运算;能力要求:能发现规律正确地进行混合计算并解决问题)
课堂作业新设计
A类:9×4÷6=6(个)
B类:9
练习十二。(教材第55、第56页)
1.通过练习,进一步帮助学生理解混合运算的顺序。
2.培养学生运用所学知识解决简单的实际问题的能力。
重点:运用混合运算解决简单的实际问题。
难点:结合具体问题理解混合运算计算顺序的合理性。
课件。
师:同学们,今天我们继续研究运用混合运算解决问题的方法和策略。
师:瞧,班级篮球对抗赛的得分情况出来了,说一说你知道了什么。(课件出示:教材第56页第8题)
学生可能会说:
·我知道这是二(1)班和二(2)班的得分情况。
·二(1)班得分是42分,二(2)班得分是38分,二(1)班获胜。
·上半场二(1)班得了24分,下半场两个班的得分一样多。
·因为二(1)班一共得了42分,上半场是24分,说明下半场得42-24=18(分)。
·算出二(1)班下半场的得分是18分,就知道二(2)班下半场的得分也是18分,因为题中已经告诉我们这两个班下半场得分一样多。
·二(2)班最后得分是38分,如果下半场得18分,那么上半场得38-18=20(分)。
……
师:你能列综合算式计算下半场二(2)班得了多少分吗
生:38-(42-24)=20(分)
师:跟同桌互相说一说,解决这个问题我们需要先计算什么 把你的思路讲给同桌听。
同桌互相交流思路,教师了解情况。
【设计意图:抽象的运算顺序与具体问题的解决相结合,帮助学生进一步理解混合运算的顺序,使学生更好地掌握解决问题的方法和策略】
师:同学们,通过今天的学习,你们学会了什么
1.在学习运用混合运算解决问题的基础上,帮助学生进一步加深对混合运算顺序的理解,使学生切身体会到数学的应用价值。
2.在具体的计算过程中,因粗心会导致结果不正确,要培养学生养成良好的学习习惯。
A类
笑笑幼儿园最近3天来了27个小朋友,照这样计算,6天要来多少个小朋友
(考查知识点:混合运算;能力要求:运用混合运算解决问题)
B类
先填空再列出综合算式。
(考查知识点:混合运算;能力要求:运用混合运算解决问题)
课堂作业新设计
A类:27÷3×6=54(个)
B类:
78-2×9=60 36÷9+78=82
教材习题
第55~56页“练习十二”
1.
5+8×2=21(元) 21>20 不够
2.
8×4-5=27(张) 说一说略
3.
80-25-37=18(棵)
4.
(25+15)÷8=5(只)
5.
37 48 56 5 33 10
6.
(60-15)÷5=9(米)
7.
应该买5个 4×5÷(5-1)=5(个)
8.
38-(42-24)=20(分)
整理和复习 练习十三。(教材第57、第58页)
1.巩固混合运算的计算顺序,能运用混合运算解决简单的实际问题。
2.引导学生系统地梳理知识,构建知识网络。
重点:学会运用混合运算解决简单的实际问题。
难点:学会系统地梳理知识,构建知识网络。
课件。
师:同学们,经过本单元的学习,你们都知道了什么
学生可能会说:
·我知道了在没有括号的算式里,如果只有加减法或只有乘除法,都要按从左往右的顺序计算。
·我知道了在没有括号的算式里,如果既有乘除法,又有加减法,要先算乘除法,后算加减法。
·我知道了算式里有括号的,要先算括号里面的。
·我还知道了如果一个问题的解决需要多个步骤,必须要知道先算什么再算什么,这样我们才能正确地运用混合运算解决问题。
……
师:同学们学会的知识真多哇!希望大家能运用这些知识解决更多的问题。
【设计意图:引导学生对所学知识进行简单有效地梳理,初步构建知识网络】
1.教学“整理和复习”第1题。
师:我们首先来做一个小练习,请你当老师,给同桌出几道本单元学过的综合算式,说一说应该先算什么再算什么,请同桌把结果计算出来,你来检查,然后两人交换角色进行。
(学生同桌之间互相出题、检查,教师巡视了解情况,对表现好的给予表扬)
2.教学“整理和复习”第2题。
师:现在请同学们去花店帮售货员阿姨算账吧!先说说你知道了什么 (课件出示:教材第57页第2题)
学生可能会说:
·有一个小朋友想买4枝康乃馨和1枝百合。
·康乃馨每枝3元,百合每枝5元。
·有位阿姨带了10元钱,想两种花各买一枝。
师:谁能先给小朋友算一算,需要多少钱
生:小朋友想买4枝康乃馨和1枝百合,就要先算出4枝康乃馨的钱数再加上1枝百合的钱就是一共需要的钱数,综合算式为:4×3+5=17(元)。
师:说得非常好。谁能帮阿姨算出买花后剩多少钱呢
生1:只要从阿姨带的10元钱里面去掉买百合的5元,再去掉买康乃馨的3元就是剩下的钱数,10-5-3=2(元)。
生2:也可以先计算出阿姨买这两种花用去多少钱,然后从10元里面去掉花的总钱数就是剩下的钱数,综合算式为:10-(5+3)=2(元)。
师:真棒!同一个问题,同学们想出了不同的解决办法,大家都肯动脑筋,值得表扬,今后要继续努力。
【设计意图:在具体情境中,培养学生思维的灵活性,提高学生解决问题的策略意识】
师:同学们,今天你有什么收获呢
学生对整个单元所学知识有了一定的认识,通过这节课的回忆,有利于学生对所学知识进行梳理并构建知识网络。注意检查学生对所学知识的掌握情况,采用同桌互相出题、检查的方式,既便于检查,又借助让学生当老师的方式有效激发学生的上进心,督促学生进行阶段性的复习巩固。
A类
有两个盒子,每个盒子里有8个乒乓球,把这些乒乓球平均分给4个运动员,每个运动员分到几个乒乓球
(考查知识点:混合运算;能力要求:能运用混合运算解决简单的实际问题)
B类
(考查知识点:混合运算;能力要求:能运用混合运算解决简单的实际问题)
课堂作业新设计
A类:8×2÷4=4(个)
B类:30÷(2×3)=5(天)
教材习题
第58页“练习十三”
1.19 30 19 30
2
6
2
6
这四组算式中,上下两个算式得数一样,运算顺序不一样
8÷2÷4 24-8-5
8÷(2×4) 24-(8+5)(答案不唯一)
2.
(17+19)÷4=9(个)
3.
80-25-38=17(本)
4.
40÷5-6=2 6+2×5=16
由于学生之前已经或多或少的接触过混合运算,只是缺乏对混合运算顺序的归纳总结,所以本单元的学习,对于学生来说没有太大难度,关键就是掌握不同情况下混合运算的计算顺序,并能熟练地进行计算。
1.使学生掌握几种不同情况下的混合运算的计算顺序,并能正确地进行计算。
2.能结合具体情境理解混合运算的计算顺序,并能熟练运用混合运算解决简单的实际问题
1.通过多种多样的练习,使学生掌握混合运算的计算顺序,提高学生的计算能力和水平。
2.结合具体的情境分析,帮助学生理解并掌握混合运算的计算顺序,为今后计算能力的提高做准备。
1 混合运算顺序
1课时
2 练习十一
1课时
3 解决问题
1课时
4 练习十二
1课时
5 整理和复习 练习十三
1课时
混合运算顺序。(教材第47~49页)
1.结合具体练习,使学生掌握混合运算的计算顺序。
2.通过多种多样的练习,提高学生的计算能力。
重点:使学生掌握混合运算的计算顺序。
难点:提高学生的计算能力。
课件。
师:同学们,我们以前学过100以内的两步连加、连减计算,你们还记得计算顺序是怎样的吗
生:100以内的两步连加、连减计算,是按从左往右的顺序计算的。
【设计意图:“温故而知新”,引导学生回忆100以内的两步连加、连减计算的顺序,为混合运算顺序的教学做准备】
1.教学例1。
师:你还记得53-24+38是按怎样的运算顺序计算的吗
生:按从左往右的顺序,先算减法再算加法。
师:好。看谁算得又对又快。
学生独立完成后,组织学生交流汇报。
师:我们以前学过的加、减、乘、除这四种运算,其实是两级不同的运算,加法和减法是同一级的运算,乘法和除法是同一级的运算。在没有括号的算式里,只有加减法或只有乘除法,都要按从左往右的顺序计算。也可以说在没有括号的算式里,只有同级运算,都要按从左往右的顺序计算。
师:计算53-24+38,为了便于看出这个综合算式的运算顺序,我们采用脱式计算,写出每次运算的结果。(边讲解边板书)
师:现在请大家像老师这样把综合算式15÷3×5的计算过程写下来。
学生独立完成计算,教师巡视了解情况,然后组织学生交流汇报。
师:接下来我们进行一场比赛,用刚才的方法计算下面各题,看谁算得又对又快。(课件出示:教材第47页“做一做”)
学生尝试独立完成练习,教师巡视,指导个别学习有困难的学生。最后组织交流汇报,对完全正确的同学给予表扬鼓励。
2.教学例2。
师:请看题目,你发现了什么 (课件出示:教材第48页例2)
生1:在跷跷板乐园里,有3组小朋友正在玩跷跷板,每组有4人。
生2:还有7位小朋友在周围观看,问跷跷板乐园一共有多少人。
师:想一想,先算什么,再算什么 怎样列式计算呢
生1:我先算跷跷板上有多少人,4×3=12(人);再算一共有多少人,12+7=19(人)。
生2:我也是这么算的,不过我列的是综合算式,4×3+7=19(人)。
生3:在我列的算式里,7+(4×3)=19(人),因为要先求4×3,就用小括号了。
师:同学们的想法都很棒!其中7+(4×3)可以写成7+4×3,因为在没有括号的算式里,如果既有乘法(或除法),又有加减法,要先算乘法(或除法),后算加减法。也可以说在没有括号的算式里,要先乘除后加减。
师:现在请同学们把下面各题第一步要先算什么圈出来。(课件出示:教材第48页“做一做”)
(教师逐一出示,学生逐一回答,教师及时做出评价,以鼓励为主)
师:现在同学们运用这个规则完成例2的计算,好吗
学生尝试独立完成计算,教师巡视了解情况。
组织学生交流汇报,重点说明运算顺序。教师结合反馈情况,进行强调讲解。
3.教学例3。
师:刚才我们说的两种情况也可以归纳为一种情况,它们都是没有括号的算式,如果在有括号的算式里,运算顺序又是怎样的 (课件出示:教材第49页最上面一句话)
学生齐读:算式里有括号的,要先算括号里面的。
师:运用这个规则,你能完成下面的习题吗 (课件出示:教材第49页例3)
学生尝试独立完成,教师巡视了解情况。
组织学生交流汇报,重点说明运算顺序。
【设计意图:层层深入,由扶到放,逐步引导学生掌握混合运算的顺序。在告诉学生运算法则的情况下,放手让学生尝试独立计算,既可以有效地锻炼学生的计算能力,又可以使学生把所学的知识点掌握牢固】
师:同学们,通过今天的学习,你们学会了什么
(在没有括号的算式里,如果只有同级运算,就按从左往右的顺序计算;如果含有两级运算,要先算乘除后算加减。算式里有括号的,要先算括号里面的)
【设计意图:课末总结能有效地帮助学生回顾本节课所学知识,使之系统化、条理化,提高课堂教学效率】
1.在学习过程中,学生不断地获得新的知识,不断产生惊喜。要经常评价学生、鼓励学生,给学生以自信。在教学过程中要耐心倾听学生的发言,热情鼓励学生,让学生感受到心与心、情与情的真诚交流。
2.以小组合作的形式组织教学,体现了“自主探索、合作交流、实践创新”的数学学习方式,培养了学生互相合作交流的意识,让学生在共同讨论中完成学习任务。
A类
(考查知识点:混合运算;能力要求:运用混合运算解决问题)
B类
在括号里填数。
8×8-( )=56 8×4+8=8×( ) 2×8-( )=7×2
(考查知识点:混合运算;能力要求:会正确地进行混合运算)
课堂作业新设计
A类:7×3+5=26(桶)
B类:8 5 2
教材习题
第49页“做一做”
1.
39 21 8 19 54 4
2.39 6 8
63 70 4
相同点:数字和运算符号相同
不同点:计算的顺序不同
3.
30 35 65-5×6 7 3 21÷(43-36)
练习十一。(教材第50~52页)
1.使学生进一步掌握混合运算的计算顺序。
2.通过巩固练习,进一步提高学生的计算能力。
重点:进一步掌握混合运算的计算顺序。
难点:进一步提高学生的计算能力。
课件。
师:同学们,通过学习混合运算顺序,你们有什么收获
学生可能会说:
·我知道了在没有括号的算式里,如果只有加减法或只有乘除法,都要按从左往右的顺序计算。
·我知道了在没有括号的算式里,如果既有乘除法,又有加减法,要先算乘除法,后算加减法。
·我知道了算式里有括号的,要先算括号里面的。
……
师:仅仅知道这些运算顺序是不够的,只有多多练习,我们才能熟练地进行混合计算。
师:仔细观察,比较上下两题的运算顺序和计算结果,说一说你发现了什么 (课件出示:教材第51页第8题)
学生尝试独立解答,然后在小组里交流,教师巡视了解情况。
组织交流汇报:
·第一组算式的区别在于上面的一题没有括号,要先算除法再算加法,这样计算的结果是21;下面的一题有括号,要先算括号里面的加法,再算括号外面的除法,这样计算的结果是5。
·第二组算式的区别同样是括号,上面的一题没有括号,要先算乘法再算减法,这样计算的结果是29;下面的一题有括号,要先算括号里面的减法,再算括号外面的乘法,这样计算的结果是20。
·我觉得这两组算式的结果之所以会不相同,跟括号有关。
·我认为是括号改变了运算顺序,所以结果才会不同。
……
(给学生足够的时间和机会发表自己的见解,正确的要给予鼓励)
师:括号的确有改变运算顺序的作用,所以在计算的时候一定要细心,看清有没有括号,弄明白先算什么再算什么,明确了运算顺序才能把题做对。
【设计意图:在具体的对比练习中,使学生认识到有没有括号很重要,提醒学生认真细心,培养学生良好的学习习惯】
师:同学们,通过今天的学习,你们收获了什么呢
1.通过这节课的学习,学生已经掌握了混合运算的计算顺序,但是计算的准确率及速度还要在进一步的练习中逐渐提高。
2.结合已有的知识经验进行教学,加上教师适时的引导启发,学生学习起来事半功倍。在学习过程中,放手让学生尝试自己解决问题,培养学生的口头表达能力和合作意识。同时在计算过程中,教师要引导学生反思,培养学生总结归纳的能力。
A类
东东去商店买了一辆小汽车,给售货员阿姨4张5元钱,售货员阿姨又找给他2元,那么这辆小汽车多少钱
(考查知识点:混合运算;能力要求:能结合实际情况,运用混合运算解决问题)
B类
小明从第1棵树跑到第5棵树,一共跑了多少米
(考查知识点:混合运算;能力要求:能结合实际情况,运用混合运算解决问题)
课堂作业新设计
A类:4×5-2=18(元)
B类:5×(5-1)=20(米)
教材习题
第50~52页“练习十一”
1.
38 58 17 9 3 54
2.8 22 3 15
15
29
5
25
21
35
7
35
23
37
9
45
3. 34-17+3 第二个计算对 18÷3×3
=17+3 =6×3
=20
=18
4.
43 17 11 19 4 59
5.
= < < <
6.
9 6 81÷9-3=6 56 88 32+7×8=88
7.
25 54 20 60 7 4
8.
21 29 5 20
9.42+14-35=21 7×9-28=35 62-(15-3)=50 50-36÷6=44
(6+6)÷3=4 (54-22)÷8=4 36÷(16÷4)=9 14÷(83-76)=2
10.
13 13 42 13 13 42
11.
82 8 8 26 9 53
12.
32 25+8×4=57(元)
13.
35-3=32(元) 32÷8=4(个)
14.
(1)12+36÷4=21 (2)(12+8)÷5=4
解决问题。(教材第53、第54页)
1.在具体情境中,运用混合运算解决简单的实际问题,进一步促使学生理解混合运算的计算顺序。
2.培养学生运用所学知识解决生活中简单的实际问题的能力。
重点:运用混合运算解决简单的实际问题。
难点:结合具体问题,理解混合运算计算顺序的合理性。
课件。
师:同学们,在我们的日常生活中有许多问题不是靠一步计算就能解决的,所以混合运算在我们日常生活中的应用很广泛。
1.教学例4。
师:看看面包师傅遇到了什么问题 你知道了什么 (课件出示:教材第53页例4)
生:知道一共要烤90个面包,已经烤了36个,剩下的每次烤9个,还需要烤多少次
师:你有办法帮面包师傅解决问题吗
生1:我们可以先计算还剩多少个没烤,90-36=54(个),把剩下的54个,每次烤9个,54里面有几个9就是需要烤多少次,54÷9=6(次)。
生2:我可以把两个算式合并成一个综合算式:(90-36)÷9。
师:用综合算式计算的时候为什么要加小括号呢
生:因为我们要先计算还剩下多少个没有烤,就必须要先算减法,那就要加小括号,否则就要先算除法了。
师:说得很有道理,老师可以教大家画图来帮助我们分析理解题意,请看:
(边画图边讲解分析)
师:该怎样思考用多个步骤解决的问题呢
生:如果一个问题需要多个步骤才能解决,要想好先算什么再算什么,才能正确解答。
2.教学“做一做”。
师:你能自己解答下面的问题吗 可以在小组里交流讨论。(课件出示:教材第54页“做一做”)
学生尝试自己解答,教师巡视了解情况。
师:谁愿意把自己的想法和结果告诉大家
学生可能会说:
·可以先计算第一组买9个花多少钱,9×3=27(元);再计算第二组买6个花多少钱,6×3=18(元),这样就可以算出第一组比第二组多花多少钱,27-18=9(元)。列成综合算式:9×3-6×3=9(元)。
·可以先计算第一组比第二组多买几个,9-6=3(个);每个3元,就是3×3=9(元)。列成综合算式:(9-6)×3=9(元)。
(如果以上两种解法学生没有答出来,教师可以介绍给学生,但是第一种解答方法不要求所有学生掌握)
【设计意图:把抽象的运算顺序与具体情境相结合,能使学生更好地掌握混合运算的顺序,突破教学重难点】
师:同学们,今天的内容你们学会了吗
在较好地掌握混合运算顺序的基础上,进行解决实际问题的教学,既能帮助学生更好地掌握运算顺序,又能使学生切身体会到数学的应用价值。但是在具体的计算过程中,因粗心等原因会导致结果不正确,因此要培养学生养成良好的学习习惯。
A类
小朋友举行队列操比赛,原来是每行9人,站了4行;老师觉得队列有点长,就想改为6行,现在每行站几个小朋友
(考查知识点:混合运算;能力要求:运用混合运算解决问题)
B类
找规律填空。
(考查知识点:混合运算;能力要求:能发现规律正确地进行混合计算并解决问题)
课堂作业新设计
A类:9×4÷6=6(个)
B类:9
练习十二。(教材第55、第56页)
1.通过练习,进一步帮助学生理解混合运算的顺序。
2.培养学生运用所学知识解决简单的实际问题的能力。
重点:运用混合运算解决简单的实际问题。
难点:结合具体问题理解混合运算计算顺序的合理性。
课件。
师:同学们,今天我们继续研究运用混合运算解决问题的方法和策略。
师:瞧,班级篮球对抗赛的得分情况出来了,说一说你知道了什么。(课件出示:教材第56页第8题)
学生可能会说:
·我知道这是二(1)班和二(2)班的得分情况。
·二(1)班得分是42分,二(2)班得分是38分,二(1)班获胜。
·上半场二(1)班得了24分,下半场两个班的得分一样多。
·因为二(1)班一共得了42分,上半场是24分,说明下半场得42-24=18(分)。
·算出二(1)班下半场的得分是18分,就知道二(2)班下半场的得分也是18分,因为题中已经告诉我们这两个班下半场得分一样多。
·二(2)班最后得分是38分,如果下半场得18分,那么上半场得38-18=20(分)。
……
师:你能列综合算式计算下半场二(2)班得了多少分吗
生:38-(42-24)=20(分)
师:跟同桌互相说一说,解决这个问题我们需要先计算什么 把你的思路讲给同桌听。
同桌互相交流思路,教师了解情况。
【设计意图:抽象的运算顺序与具体问题的解决相结合,帮助学生进一步理解混合运算的顺序,使学生更好地掌握解决问题的方法和策略】
师:同学们,通过今天的学习,你们学会了什么
1.在学习运用混合运算解决问题的基础上,帮助学生进一步加深对混合运算顺序的理解,使学生切身体会到数学的应用价值。
2.在具体的计算过程中,因粗心会导致结果不正确,要培养学生养成良好的学习习惯。
A类
笑笑幼儿园最近3天来了27个小朋友,照这样计算,6天要来多少个小朋友
(考查知识点:混合运算;能力要求:运用混合运算解决问题)
B类
先填空再列出综合算式。
(考查知识点:混合运算;能力要求:运用混合运算解决问题)
课堂作业新设计
A类:27÷3×6=54(个)
B类:
78-2×9=60 36÷9+78=82
教材习题
第55~56页“练习十二”
1.
5+8×2=21(元) 21>20 不够
2.
8×4-5=27(张) 说一说略
3.
80-25-37=18(棵)
4.
(25+15)÷8=5(只)
5.
37 48 56 5 33 10
6.
(60-15)÷5=9(米)
7.
应该买5个 4×5÷(5-1)=5(个)
8.
38-(42-24)=20(分)
整理和复习 练习十三。(教材第57、第58页)
1.巩固混合运算的计算顺序,能运用混合运算解决简单的实际问题。
2.引导学生系统地梳理知识,构建知识网络。
重点:学会运用混合运算解决简单的实际问题。
难点:学会系统地梳理知识,构建知识网络。
课件。
师:同学们,经过本单元的学习,你们都知道了什么
学生可能会说:
·我知道了在没有括号的算式里,如果只有加减法或只有乘除法,都要按从左往右的顺序计算。
·我知道了在没有括号的算式里,如果既有乘除法,又有加减法,要先算乘除法,后算加减法。
·我知道了算式里有括号的,要先算括号里面的。
·我还知道了如果一个问题的解决需要多个步骤,必须要知道先算什么再算什么,这样我们才能正确地运用混合运算解决问题。
……
师:同学们学会的知识真多哇!希望大家能运用这些知识解决更多的问题。
【设计意图:引导学生对所学知识进行简单有效地梳理,初步构建知识网络】
1.教学“整理和复习”第1题。
师:我们首先来做一个小练习,请你当老师,给同桌出几道本单元学过的综合算式,说一说应该先算什么再算什么,请同桌把结果计算出来,你来检查,然后两人交换角色进行。
(学生同桌之间互相出题、检查,教师巡视了解情况,对表现好的给予表扬)
2.教学“整理和复习”第2题。
师:现在请同学们去花店帮售货员阿姨算账吧!先说说你知道了什么 (课件出示:教材第57页第2题)
学生可能会说:
·有一个小朋友想买4枝康乃馨和1枝百合。
·康乃馨每枝3元,百合每枝5元。
·有位阿姨带了10元钱,想两种花各买一枝。
师:谁能先给小朋友算一算,需要多少钱
生:小朋友想买4枝康乃馨和1枝百合,就要先算出4枝康乃馨的钱数再加上1枝百合的钱就是一共需要的钱数,综合算式为:4×3+5=17(元)。
师:说得非常好。谁能帮阿姨算出买花后剩多少钱呢
生1:只要从阿姨带的10元钱里面去掉买百合的5元,再去掉买康乃馨的3元就是剩下的钱数,10-5-3=2(元)。
生2:也可以先计算出阿姨买这两种花用去多少钱,然后从10元里面去掉花的总钱数就是剩下的钱数,综合算式为:10-(5+3)=2(元)。
师:真棒!同一个问题,同学们想出了不同的解决办法,大家都肯动脑筋,值得表扬,今后要继续努力。
【设计意图:在具体情境中,培养学生思维的灵活性,提高学生解决问题的策略意识】
师:同学们,今天你有什么收获呢
学生对整个单元所学知识有了一定的认识,通过这节课的回忆,有利于学生对所学知识进行梳理并构建知识网络。注意检查学生对所学知识的掌握情况,采用同桌互相出题、检查的方式,既便于检查,又借助让学生当老师的方式有效激发学生的上进心,督促学生进行阶段性的复习巩固。
A类
有两个盒子,每个盒子里有8个乒乓球,把这些乒乓球平均分给4个运动员,每个运动员分到几个乒乓球
(考查知识点:混合运算;能力要求:能运用混合运算解决简单的实际问题)
B类
(考查知识点:混合运算;能力要求:能运用混合运算解决简单的实际问题)
课堂作业新设计
A类:8×2÷4=4(个)
B类:30÷(2×3)=5(天)
教材习题
第58页“练习十三”
1.19 30 19 30
2
6
2
6
这四组算式中,上下两个算式得数一样,运算顺序不一样
8÷2÷4 24-8-5
8÷(2×4) 24-(8+5)(答案不唯一)
2.
(17+19)÷4=9(个)
3.
80-25-38=17(本)
4.
40÷5-6=2 6+2×5=16
