黑龙江省伊春市带岭高级中学人教版高中物理选修3-5课件_16.4 碰撞 (共22张PPT)
文档属性
| 名称 | 黑龙江省伊春市带岭高级中学人教版高中物理选修3-5课件_16.4 碰撞 (共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2017-09-24 00:00:00 | ||
图片预览







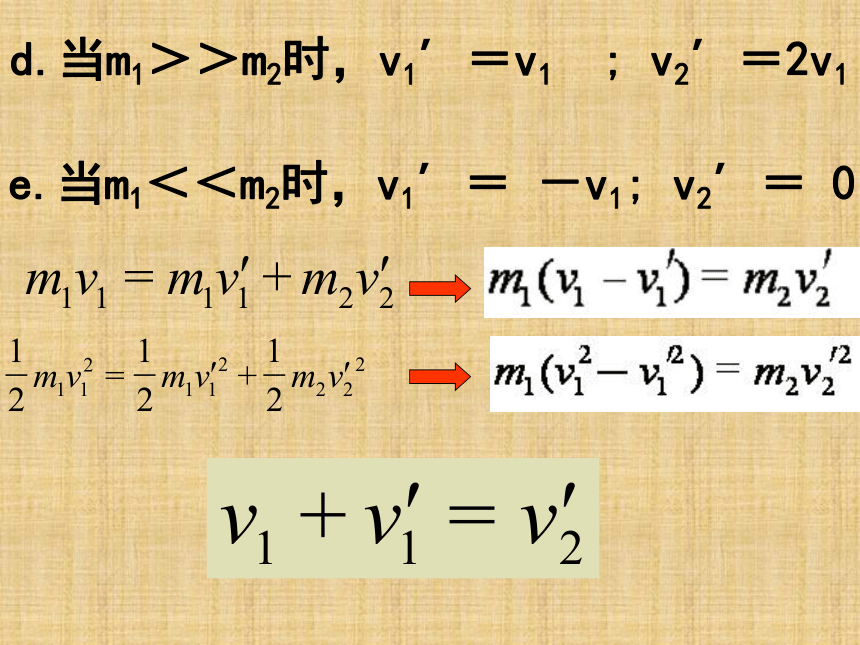
文档简介
课件22张PPT。 §16.4 碰 撞(一)碰撞的共性与个性1、共性:
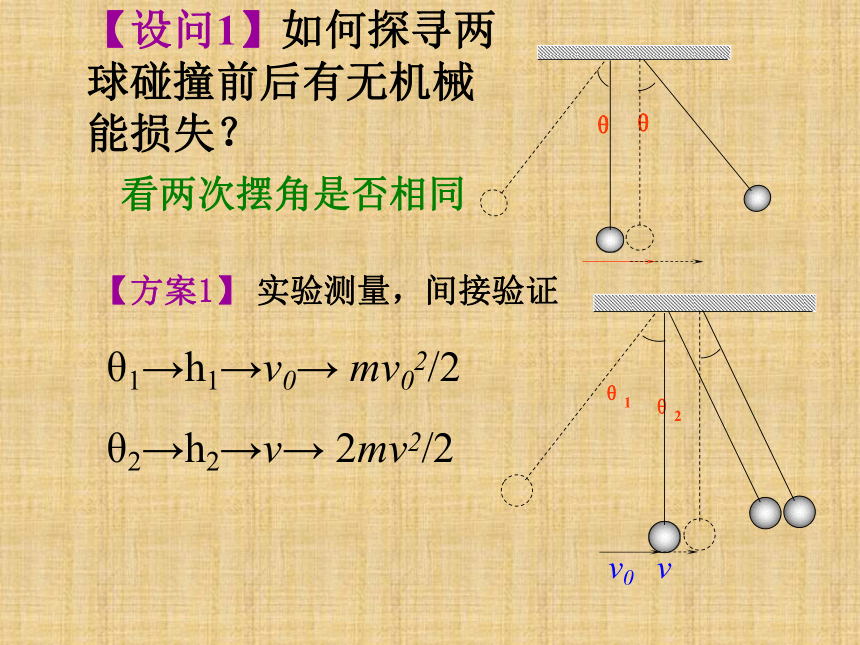
作用力变化快 有些碰撞碰后分开,有些碰撞碰后粘在一起; 相互作用时间短作用力峰值大系统动量守恒2、个性:有些碰撞沿一条直线,有些碰不在一条直线上; 有些碰撞过程可能机械能守恒,有些过程机械能可能不守恒……【方案1】 实验测量,间接验证θ2θ1θ1→h1→v0→ mv02/2
θ2→h2→v→ 2mv2/2θθ【设问1】如何探寻两球碰撞前后有无机械能损失? 看两次摆角是否相同由动量守恒定律: 碰撞前系统总动能: 碰撞后系统总动能: 碰撞过程中有机械能损失【方案2】 :理论论证 分类方式之一:从能量变化方面分类(二)碰撞的分类碰撞过程中机械能守恒碰撞过程中机械能不守恒碰撞后两物粘合在一起,以共同速度运动1、弹性碰撞:2、非弹性碰撞:3、完全非弹性碰撞:机械能损失最大!【讨论问题一】一维弹性碰撞的碰后速度的确定 假设物体m1以速度V1与原来静止的物体m2发生弹性碰撞,碰撞后他们的速度分别为V1’和V2’ 。求出用m1 m2 V1 来表示V1’和V2’的表达式。 弹性碰撞:动量和机械能都守恒讨论:a.当m1=m2时,v1’=0; v2’=v1
(质量相等,交换速度)b.当m1>m2时, v1’>0 ; v2’>0.
(大碰小,一起跑)c.当m1<m2时, v1’<0; v2’>0.
(小碰大,要反弹)d.当m1>>m2时,v1’=v1 ; v2’=2v1e.当m1<<m2时,v1’= -v1; v2’= 0【讨论问题二】
碰撞过程中能量与形变量的演变——碰撞过程的“慢镜头”【例2】质量为m速度为v的A球,跟质量为3m的静止B球发生正碰,碰撞可能是弹性,也可能非弹性,碰后B球的速度可能是以下值吗?
(A)0.6v (B)0.4v (C)0.2v解:B球速度的最小值发生在完全非弹性碰撞情形
由动量守恒:B球速度的最大值发生在弹性碰撞时:∵所以,只有0.4v是速度可能值
分类方式之二:从碰撞速度方向分类 1、对心碰撞——正碰:
2、非对心碰撞——斜碰:碰前运动速度与两球心连线处于同一直线上
碰前运动速度与两球心连线不在同一直线上
【设问】斜碰过程满足动量守恒吗?为什么?如图,能否大致画出碰后A球的速度方向?【设问】若两球质量相等,又是弹性碰撞你能进一步确定两球碰后速度方向关系吗?
1、动量制约2、动能制约
3、运动制约
(三)碰撞规律总结【例3】在光滑水平面上,动能为E0、动量的大小为P0的小钢球1与静止的小钢球2发生碰撞,碰撞前后球1的运动方向相反,将碰撞后球1的动能和动量的大小分别记为E1、P1,球2的动能和动量的大小分别记为E2、P2,则必有:
A、E1E0 D、P2>P0参考答案:DAB——守恒——不增——合理 在光滑水平面上,有A、B两个小球向右沿同一直线运动,取向右为正,两球的动量分别是pA=5kgm/s,pB=7kgm/s,如图所示.若能发生正碰,则碰后两球的动量增量△pA、△pB可能是??( )
A.△pA=-3kgm/s;△pB =3kgm/s B.△pA=3kgm/s;△pB =3kgm/s
C.△pA= -10kgm/s;△pB =10kgm/s D.△pA=3kgm/s;△pB = -3kgm/s A【思考】(四)微观世界碰撞现象1、中子的发现:1932年查德威克(英国)(四)微观世界碰撞现象2、中子减速剂:石墨、重水(四)微观世界碰撞现象3、验证汞原子能量量子化的经典实验——弗兰克—赫兹实验(1914年) 通过电子与汞原子核碰撞的能量传递,证实了原子能量处于分立的不连续状态(四)微观世界碰撞现象4、粒子加速器基本知识点弹性碰撞→动量、机械能守恒非弹性碰撞→动量守恒、机械能有损失完全非弹性碰撞→动量守恒、机械能损失最大基本思想方法猜想推论小结:对心碰撞(正碰)→碰撞前后速度沿球心连线非对心碰撞(斜碰)→碰撞前后速度不共线验证结束语: 大到茫茫宇宙,小到神秘微观,平凡到日常生活,有着形形色色、风格迥异的碰撞现象,虽然它们的运动个性十足,但都遵守两条铁的纪律:动量守恒和动能不增,这两条规律就两只无形的手,操纵和控制着事物发展的方向和进程,寻求大千世界变化中的不变量,找到它,我们就能掌握事物变化的规律,这也是物理学探寻未知世界基本的思想方法 !
【拓展与应用】 → → 【例1】“瑞士天王”费德勒在一次比赛中,面对迎面飞来的速度为60km/h的网球,挥动球拍以70km/h的速度击球,打出一记“平击球”,试估算此次击球的球速。解:网球拍与网球碰撞为完全弹性,球拍质量远大于球质量碰前球、拍接近速度 60km/h+70km/h=130km/h碰后球、拍分离速度亦为 130km/h击球后球拍速度不变,故球速为130km/h+70km/h
=200km/h
作用力变化快 有些碰撞碰后分开,有些碰撞碰后粘在一起; 相互作用时间短作用力峰值大系统动量守恒2、个性:有些碰撞沿一条直线,有些碰不在一条直线上; 有些碰撞过程可能机械能守恒,有些过程机械能可能不守恒……【方案1】 实验测量,间接验证θ2θ1θ1→h1→v0→ mv02/2
θ2→h2→v→ 2mv2/2θθ【设问1】如何探寻两球碰撞前后有无机械能损失? 看两次摆角是否相同由动量守恒定律: 碰撞前系统总动能: 碰撞后系统总动能: 碰撞过程中有机械能损失【方案2】 :理论论证 分类方式之一:从能量变化方面分类(二)碰撞的分类碰撞过程中机械能守恒碰撞过程中机械能不守恒碰撞后两物粘合在一起,以共同速度运动1、弹性碰撞:2、非弹性碰撞:3、完全非弹性碰撞:机械能损失最大!【讨论问题一】一维弹性碰撞的碰后速度的确定 假设物体m1以速度V1与原来静止的物体m2发生弹性碰撞,碰撞后他们的速度分别为V1’和V2’ 。求出用m1 m2 V1 来表示V1’和V2’的表达式。 弹性碰撞:动量和机械能都守恒讨论:a.当m1=m2时,v1’=0; v2’=v1
(质量相等,交换速度)b.当m1>m2时, v1’>0 ; v2’>0.
(大碰小,一起跑)c.当m1<m2时, v1’<0; v2’>0.
(小碰大,要反弹)d.当m1>>m2时,v1’=v1 ; v2’=2v1e.当m1<<m2时,v1’= -v1; v2’= 0【讨论问题二】
碰撞过程中能量与形变量的演变——碰撞过程的“慢镜头”【例2】质量为m速度为v的A球,跟质量为3m的静止B球发生正碰,碰撞可能是弹性,也可能非弹性,碰后B球的速度可能是以下值吗?
(A)0.6v (B)0.4v (C)0.2v解:B球速度的最小值发生在完全非弹性碰撞情形
由动量守恒:B球速度的最大值发生在弹性碰撞时:∵所以,只有0.4v是速度可能值
分类方式之二:从碰撞速度方向分类 1、对心碰撞——正碰:
2、非对心碰撞——斜碰:碰前运动速度与两球心连线处于同一直线上
碰前运动速度与两球心连线不在同一直线上
【设问】斜碰过程满足动量守恒吗?为什么?如图,能否大致画出碰后A球的速度方向?【设问】若两球质量相等,又是弹性碰撞你能进一步确定两球碰后速度方向关系吗?
1、动量制约2、动能制约
3、运动制约
(三)碰撞规律总结【例3】在光滑水平面上,动能为E0、动量的大小为P0的小钢球1与静止的小钢球2发生碰撞,碰撞前后球1的运动方向相反,将碰撞后球1的动能和动量的大小分别记为E1、P1,球2的动能和动量的大小分别记为E2、P2,则必有:
A、E1
A.△pA=-3kgm/s;△pB =3kgm/s B.△pA=3kgm/s;△pB =3kgm/s
C.△pA= -10kgm/s;△pB =10kgm/s D.△pA=3kgm/s;△pB = -3kgm/s A【思考】(四)微观世界碰撞现象1、中子的发现:1932年查德威克(英国)(四)微观世界碰撞现象2、中子减速剂:石墨、重水(四)微观世界碰撞现象3、验证汞原子能量量子化的经典实验——弗兰克—赫兹实验(1914年) 通过电子与汞原子核碰撞的能量传递,证实了原子能量处于分立的不连续状态(四)微观世界碰撞现象4、粒子加速器基本知识点弹性碰撞→动量、机械能守恒非弹性碰撞→动量守恒、机械能有损失完全非弹性碰撞→动量守恒、机械能损失最大基本思想方法猜想推论小结:对心碰撞(正碰)→碰撞前后速度沿球心连线非对心碰撞(斜碰)→碰撞前后速度不共线验证结束语: 大到茫茫宇宙,小到神秘微观,平凡到日常生活,有着形形色色、风格迥异的碰撞现象,虽然它们的运动个性十足,但都遵守两条铁的纪律:动量守恒和动能不增,这两条规律就两只无形的手,操纵和控制着事物发展的方向和进程,寻求大千世界变化中的不变量,找到它,我们就能掌握事物变化的规律,这也是物理学探寻未知世界基本的思想方法 !
【拓展与应用】 → → 【例1】“瑞士天王”费德勒在一次比赛中,面对迎面飞来的速度为60km/h的网球,挥动球拍以70km/h的速度击球,打出一记“平击球”,试估算此次击球的球速。解:网球拍与网球碰撞为完全弹性,球拍质量远大于球质量碰前球、拍接近速度 60km/h+70km/h=130km/h碰后球、拍分离速度亦为 130km/h击球后球拍速度不变,故球速为130km/h+70km/h
=200km/h
