广东省佛山市高明区高中数学第二章数列2.5数列求和的求法(1)教案新人教A版必修5
文档属性
| 名称 | 广东省佛山市高明区高中数学第二章数列2.5数列求和的求法(1)教案新人教A版必修5 |  | |
| 格式 | zip | ||
| 文件大小 | 83.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-26 14:38:13 | ||
图片预览

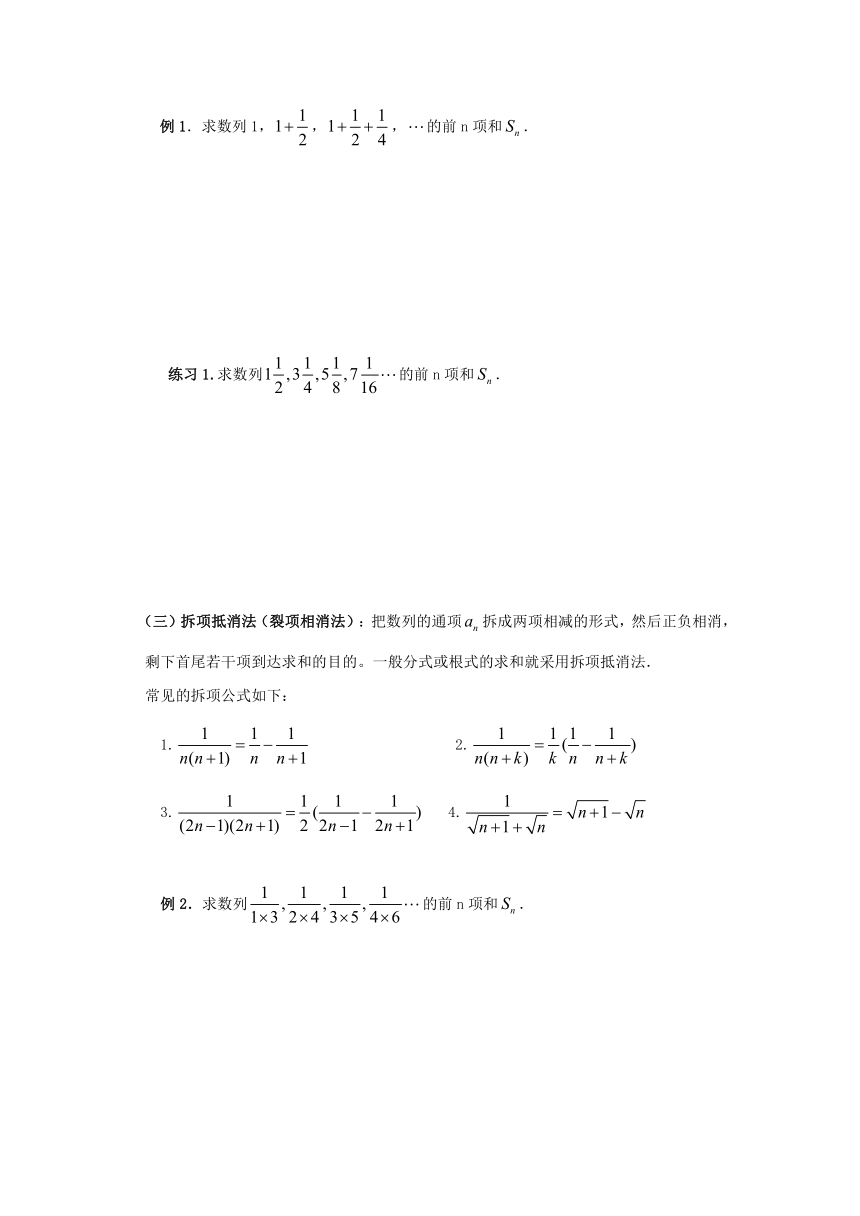
文档简介
2.7
数列的求和(1)
【学习目标】
1.熟练的掌握数列求和的常用方法.
2.熟练的掌握数列求和的常见题型和常用的变形技巧.
【重点难点】
重点:三种求和方法.
难点:
.
【学法指导】
求数列前n项和时一定要先求通项公式,再根据通项公式的特点灵活的选择方法,熟练掌握每个方法的格式.
一.课前预习
1.数列中,,且,
.
2.数列中,,且,
.
3..
4..
二.课堂学习与研讨
数列求和的常用方法:
(一)公式法:所给数列已为等差或等比数列,则直接利用等差,等比的求和公式求,或直接利用公式求和,如课前预习的四个题
(二)分组求和法:把数列的通项分解成一些可以求和的数列,如等差或等比数列
例1.求数列1,,,的前n项和.
练习1.求数列的前n项和.
(三)拆项抵消法(裂项相消法):把数列的通项拆成两项相减的形式,然后正负相消,剩下首尾若干项到达求和的目的。一般分式或根式的求和就采用拆项抵消法.
常见的拆项公式如下:
1.
2.
3.
4.
例2.求数列的前n项和.
例3.求数列的前n项和.
练习2.求.
三.课堂检测
1.求数列的前n项和.
2.求数列的前n项和.
3.求数列的前n项和.
四.作业
1.求数列7,
77,777,的前n项和.
2.求数列的前n项和.
3.求数列的前n项和.
数列的求和(1)
【学习目标】
1.熟练的掌握数列求和的常用方法.
2.熟练的掌握数列求和的常见题型和常用的变形技巧.
【重点难点】
重点:三种求和方法.
难点:
.
【学法指导】
求数列前n项和时一定要先求通项公式,再根据通项公式的特点灵活的选择方法,熟练掌握每个方法的格式.
一.课前预习
1.数列中,,且,
.
2.数列中,,且,
.
3..
4..
二.课堂学习与研讨
数列求和的常用方法:
(一)公式法:所给数列已为等差或等比数列,则直接利用等差,等比的求和公式求,或直接利用公式求和,如课前预习的四个题
(二)分组求和法:把数列的通项分解成一些可以求和的数列,如等差或等比数列
例1.求数列1,,,的前n项和.
练习1.求数列的前n项和.
(三)拆项抵消法(裂项相消法):把数列的通项拆成两项相减的形式,然后正负相消,剩下首尾若干项到达求和的目的。一般分式或根式的求和就采用拆项抵消法.
常见的拆项公式如下:
1.
2.
3.
4.
例2.求数列的前n项和.
例3.求数列的前n项和.
练习2.求.
三.课堂检测
1.求数列的前n项和.
2.求数列的前n项和.
3.求数列的前n项和.
四.作业
1.求数列7,
77,777,的前n项和.
2.求数列的前n项和.
3.求数列的前n项和.
