湖北省丹江口市第一中学高中物理选修3-4课件:第十一章 单摆 (共36张PPT)
文档属性
| 名称 | 湖北省丹江口市第一中学高中物理选修3-4课件:第十一章 单摆 (共36张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2017-09-25 13:57:45 | ||
图片预览









文档简介
课件36张PPT。单
摆物体在竖直平面内的摆动你还知道
哪些?吊灯风铃秋千摆钟 类比:弹簧振子模型的建立—— 构模:我们对实际生活中的摆进行理想化处理,忽略次要因素 、突出主要因素,这样所构建的模型称之为单摆。思考:如何把复杂的实际问题简单化呢?阅读:教材第13页 排除干扰因素、忽略次要因素 、突出主要因素。§11.4 单 摆一、概念2、摆长:悬点到摆球重心的距离叫做摆长。1、单摆:细线一端固定在悬点,另一端系一个小球,如果细线的质量与小球相比可以忽略;球的直径与线的长度相比也可以忽略,这样的装置就叫做单摆。摆长 L=L0+R①摆线质量m 远小于摆球质量 M,即m << M 。3、单摆理想化条件是:③摆球所受空气阻力远小于摆球重力及绳的拉力,可忽略不计。②摆球的直径 d远小于单摆的摆长L,即 d <<L。④摆线的伸长量很小,可以忽略。4、单摆是对现实摆的抽象,是一种理想化的物理模型。我们在生活中
见到的摆
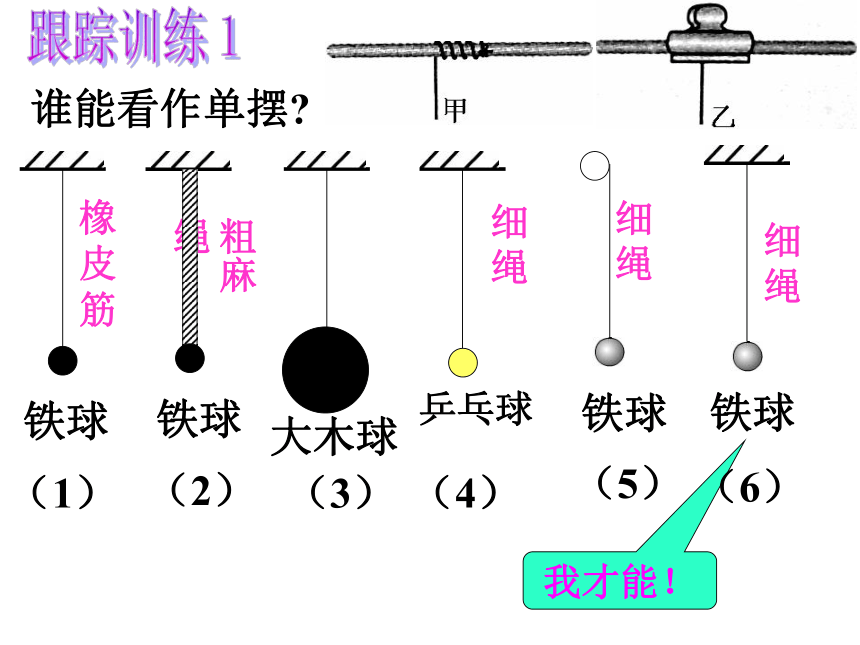
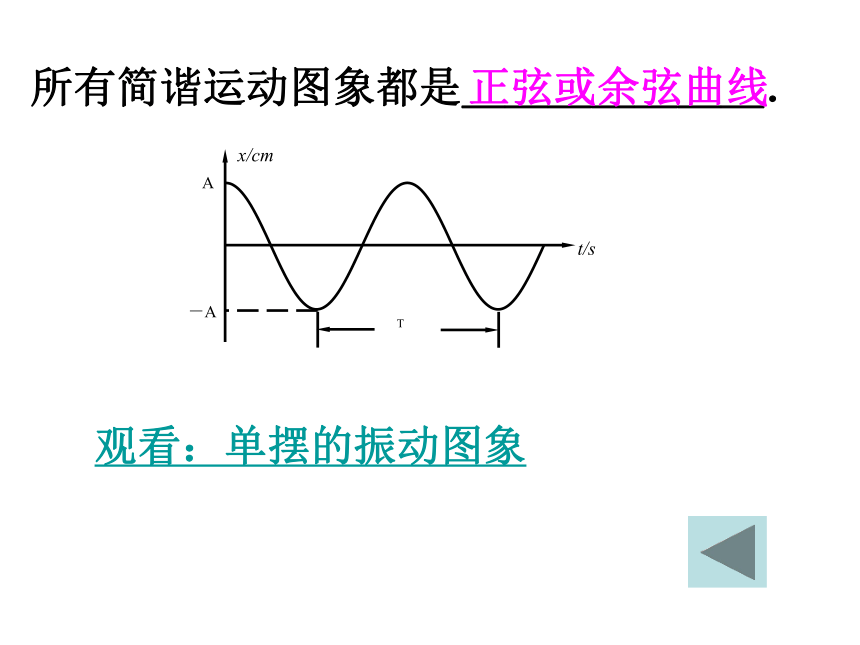
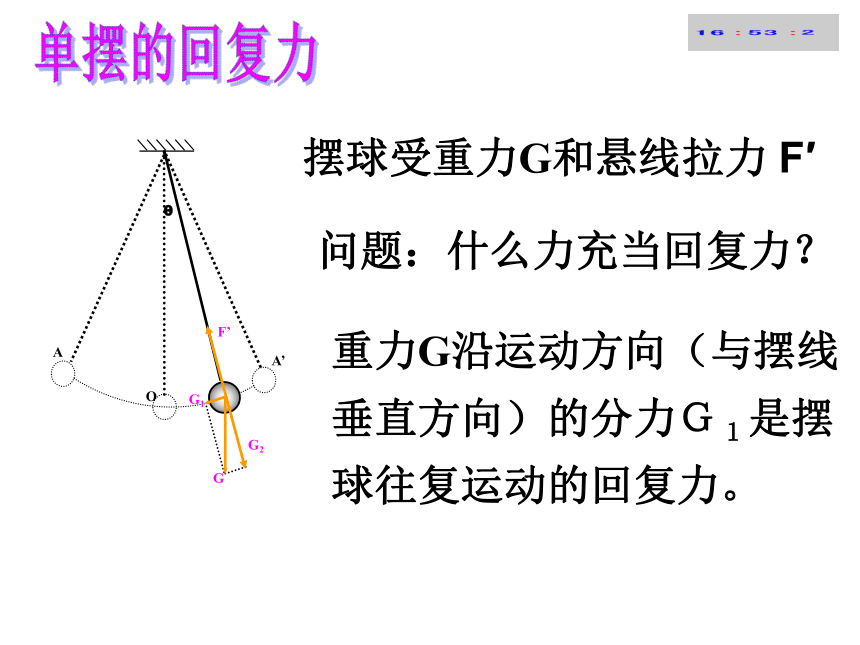
是单摆吗?谁能看作单摆?我才能!跟踪训练1问题:单摆振动是简谐运动吗?猜想:是?不是?问题:如何验证?方法一:从单摆的振动图象判断方法二:从单摆的受力特征判断二、单摆振动性质的探究 所有简谐运动图象都是_______.观看:单摆的振动图象正弦或余弦曲线简谐运动的回复力特征? 回复力的大小与位移的大小成正比,回复力的方向与位移的方向相反。分析单摆的回复力摆球受重力G和悬线拉力 F′单摆的回复力重力G沿运动方向(与摆线垂直方向)的分力G1是摆球往复运动的回复力。问题:什么力充当回复力?F回=G1=G?sin??: F= -kx设小球运动到任意点P时,摆线与 竖直方向的夹角为θ,摆球偏离平衡位置的位移为x,摆长为L小球摆动的回复力F为:单摆的回复力θSinθ=?单摆的回复力正比于x吗?单摆的回复力? 很小时:单摆的回复力单摆的回复力所以单摆的回复力大小为考虑到回复力的方向与位移的方向_____,所以:故相反单摆的回复力单摆的回复力在偏角很小的情况下,满足:结论:F=-kx所以,在偏角很小(θ<10°)的情况下,单摆的振动是简谐运动。2、下列关于单摆的说法正确的是 ( )
A.摆球经过平衡位置时其合力为零.
B.摆球经过平衡位置时其回复力为零.
C.单摆作简谐运动的回复力是由摆球重力沿圆弧切线的分力提供的.
D.单摆作简谐运动的回复力是由摆球重力与摆线拉力的合力提供的.BC跟踪训练2探讨摆球做哪些形式的运动?②以悬点O/为圆心的圆周运动。①以点O为平衡位置的振动。 在偏角很小的情况下,单摆的振动是简谐运动。摆球经过平衡位置时:注意:平衡位置的含义----所受的回复力为零,但合外力不一定为零!探讨悬线拉力F′与摆球重力G的合力的作用F ′与G的合力即为F回与F向的合力。三、单摆振动周期的初探单摆振动周期与哪些因素有关呢?1、猜想? 单摆的摆长、摆球质量、振幅2、实验验证①方法:___________.②注意: 摆角________.当地的重力加速度控制变量法 小于10°?材料鉴赏:一位广州人冬天去哈尔滨旅游,在一家大型超市以高价购买了一台精致的摆钟,买的时候发现它走时很准。回到广州不到两天就走时相差一分多钟。于是大呼上当,心里极其气愤。后来,他求助了“消费者权益保护协会”,准备与该超市打一场索赔官司,消费者协会调查研究发现产品货真价实,那么问题出在哪儿呢?3、演示实验(定性分析)演示实验1:单摆的周期与单摆的振幅有没有关系?实验结论1:单摆的周期与单摆的振幅______.无关(单摆的等时性)演示实验2:单摆的周期与摆球的质量有没有关系?实验结论2:单摆的周期与摆球的质量______.无关重力加速度越大(小),周期越小(大)3、演示实验(定性分析)演示实验3:单摆的周期与摆长有没有关系?实验结论3:单摆的周期与摆长______.有关摆长越长(短),周期越大(小)实验剪辑4:单摆的周期与重力加速度有没有关系?实验结论4:单摆的周期与重力加速度______.有关B3、下述哪些情况可使单摆(?<100)的振动周期增大( )
A.摆球的质量增大
B.摆长增大
C.单摆由赤道移到北极
D.增大振幅跟踪训练3一、知识小结二、方法小结1、单摆模型3、单摆振动周期的初探2、单摆振动性质的探究1、类比思维法3、控制变量法2、理想化方法作业:1、预习单摆周期公式及其应用2、同步导学P22 2、5、7 关于单摆振动的回复力是什么,有以下两种观点:
(1)“合力观”:单摆振动的回复力是摆球受到的重力和绳的拉力的合力。理由是像弹簧振子一样,振动物体的加速度是由合力产生的。
(2)“分力观”:单摆振动的回复力是摆球受到的重力沿圆弧切线方向的分力。理由是摆球的加速度是由此力产生的。
你认为这两种观点和理由是否正确,说明你的理由。课后思考题§11.4 单 摆一、概念1、单摆:
2、摆长:
3、单摆理想化条件:
4、单摆是一种理想模型。二、单摆振动性质的探究1、单摆的振动图象
2、单摆的回复力
3、结论:在偏角很小(θ<10°)的情况下,单摆的振动是简谐运动。三、单摆振动周期的初探1、猜想
2、实验验证
①教师演示实验(定性分析)
②学生分组实验(定量探究)
板书设计材料鉴赏: “单摆等时性”的研究 1862年,18岁的伽利略离开神学院进入比萨大学学习医学,他的心中充满着奇妙的幻想和对自然科学的无穷疑问,一次他在比萨大学忘掉了向上帝祈祷,双眼注视着天花板上悬垂下来摇摆不定的挂灯,右手按着左手的脉搏,口中默默地数着数字,在一般人熟视无睹的现象中,他却第一个明白了挂灯每摆动一次的时间是相等的,这就是单摆摆动的等时性规律。后来他利用这个原理制成了一个“脉动器”,又叫“脉搏计”,使其摆动的快慢跟正常人脉搏跳动的快慢相一致,从而帮助判断病人患病的情况,这就是“摆”的最初应用。1.组成单摆的最佳组合是( )
A.长为1米的细线
B.长为1米的细铁丝
C.长为1米的橡皮条
D.长为0.2米的细丝线
E.直径为5厘米的钢球
F.直径为5厘米的泡沫塑料球
G.直径为1厘米的钢球
H.直径为1厘米的塑料球A G返回返回
摆物体在竖直平面内的摆动你还知道
哪些?吊灯风铃秋千摆钟 类比:弹簧振子模型的建立—— 构模:我们对实际生活中的摆进行理想化处理,忽略次要因素 、突出主要因素,这样所构建的模型称之为单摆。思考:如何把复杂的实际问题简单化呢?阅读:教材第13页 排除干扰因素、忽略次要因素 、突出主要因素。§11.4 单 摆一、概念2、摆长:悬点到摆球重心的距离叫做摆长。1、单摆:细线一端固定在悬点,另一端系一个小球,如果细线的质量与小球相比可以忽略;球的直径与线的长度相比也可以忽略,这样的装置就叫做单摆。摆长 L=L0+R①摆线质量m 远小于摆球质量 M,即m << M 。3、单摆理想化条件是:③摆球所受空气阻力远小于摆球重力及绳的拉力,可忽略不计。②摆球的直径 d远小于单摆的摆长L,即 d <<L。④摆线的伸长量很小,可以忽略。4、单摆是对现实摆的抽象,是一种理想化的物理模型。我们在生活中
见到的摆
是单摆吗?谁能看作单摆?我才能!跟踪训练1问题:单摆振动是简谐运动吗?猜想:是?不是?问题:如何验证?方法一:从单摆的振动图象判断方法二:从单摆的受力特征判断二、单摆振动性质的探究 所有简谐运动图象都是_______.观看:单摆的振动图象正弦或余弦曲线简谐运动的回复力特征? 回复力的大小与位移的大小成正比,回复力的方向与位移的方向相反。分析单摆的回复力摆球受重力G和悬线拉力 F′单摆的回复力重力G沿运动方向(与摆线垂直方向)的分力G1是摆球往复运动的回复力。问题:什么力充当回复力?F回=G1=G?sin??: F= -kx设小球运动到任意点P时,摆线与 竖直方向的夹角为θ,摆球偏离平衡位置的位移为x,摆长为L小球摆动的回复力F为:单摆的回复力θSinθ=?单摆的回复力正比于x吗?单摆的回复力? 很小时:单摆的回复力单摆的回复力所以单摆的回复力大小为考虑到回复力的方向与位移的方向_____,所以:故相反单摆的回复力单摆的回复力在偏角很小的情况下,满足:结论:F=-kx所以,在偏角很小(θ<10°)的情况下,单摆的振动是简谐运动。2、下列关于单摆的说法正确的是 ( )
A.摆球经过平衡位置时其合力为零.
B.摆球经过平衡位置时其回复力为零.
C.单摆作简谐运动的回复力是由摆球重力沿圆弧切线的分力提供的.
D.单摆作简谐运动的回复力是由摆球重力与摆线拉力的合力提供的.BC跟踪训练2探讨摆球做哪些形式的运动?②以悬点O/为圆心的圆周运动。①以点O为平衡位置的振动。 在偏角很小的情况下,单摆的振动是简谐运动。摆球经过平衡位置时:注意:平衡位置的含义----所受的回复力为零,但合外力不一定为零!探讨悬线拉力F′与摆球重力G的合力的作用F ′与G的合力即为F回与F向的合力。三、单摆振动周期的初探单摆振动周期与哪些因素有关呢?1、猜想? 单摆的摆长、摆球质量、振幅2、实验验证①方法:___________.②注意: 摆角________.当地的重力加速度控制变量法 小于10°?材料鉴赏:一位广州人冬天去哈尔滨旅游,在一家大型超市以高价购买了一台精致的摆钟,买的时候发现它走时很准。回到广州不到两天就走时相差一分多钟。于是大呼上当,心里极其气愤。后来,他求助了“消费者权益保护协会”,准备与该超市打一场索赔官司,消费者协会调查研究发现产品货真价实,那么问题出在哪儿呢?3、演示实验(定性分析)演示实验1:单摆的周期与单摆的振幅有没有关系?实验结论1:单摆的周期与单摆的振幅______.无关(单摆的等时性)演示实验2:单摆的周期与摆球的质量有没有关系?实验结论2:单摆的周期与摆球的质量______.无关重力加速度越大(小),周期越小(大)3、演示实验(定性分析)演示实验3:单摆的周期与摆长有没有关系?实验结论3:单摆的周期与摆长______.有关摆长越长(短),周期越大(小)实验剪辑4:单摆的周期与重力加速度有没有关系?实验结论4:单摆的周期与重力加速度______.有关B3、下述哪些情况可使单摆(?<100)的振动周期增大( )
A.摆球的质量增大
B.摆长增大
C.单摆由赤道移到北极
D.增大振幅跟踪训练3一、知识小结二、方法小结1、单摆模型3、单摆振动周期的初探2、单摆振动性质的探究1、类比思维法3、控制变量法2、理想化方法作业:1、预习单摆周期公式及其应用2、同步导学P22 2、5、7 关于单摆振动的回复力是什么,有以下两种观点:
(1)“合力观”:单摆振动的回复力是摆球受到的重力和绳的拉力的合力。理由是像弹簧振子一样,振动物体的加速度是由合力产生的。
(2)“分力观”:单摆振动的回复力是摆球受到的重力沿圆弧切线方向的分力。理由是摆球的加速度是由此力产生的。
你认为这两种观点和理由是否正确,说明你的理由。课后思考题§11.4 单 摆一、概念1、单摆:
2、摆长:
3、单摆理想化条件:
4、单摆是一种理想模型。二、单摆振动性质的探究1、单摆的振动图象
2、单摆的回复力
3、结论:在偏角很小(θ<10°)的情况下,单摆的振动是简谐运动。三、单摆振动周期的初探1、猜想
2、实验验证
①教师演示实验(定性分析)
②学生分组实验(定量探究)
板书设计材料鉴赏: “单摆等时性”的研究 1862年,18岁的伽利略离开神学院进入比萨大学学习医学,他的心中充满着奇妙的幻想和对自然科学的无穷疑问,一次他在比萨大学忘掉了向上帝祈祷,双眼注视着天花板上悬垂下来摇摆不定的挂灯,右手按着左手的脉搏,口中默默地数着数字,在一般人熟视无睹的现象中,他却第一个明白了挂灯每摆动一次的时间是相等的,这就是单摆摆动的等时性规律。后来他利用这个原理制成了一个“脉动器”,又叫“脉搏计”,使其摆动的快慢跟正常人脉搏跳动的快慢相一致,从而帮助判断病人患病的情况,这就是“摆”的最初应用。1.组成单摆的最佳组合是( )
A.长为1米的细线
B.长为1米的细铁丝
C.长为1米的橡皮条
D.长为0.2米的细丝线
E.直径为5厘米的钢球
F.直径为5厘米的泡沫塑料球
G.直径为1厘米的钢球
H.直径为1厘米的塑料球A G返回返回
