第三章 位置与坐标单元测试卷(含答案与解析)
文档属性
| 名称 | 第三章 位置与坐标单元测试卷(含答案与解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 949.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-24 00:00:00 | ||
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
【新北师大版八年级数学(上)单元测试卷】
第三章《位置与坐标》(含答案与解析)
班级:___________ 姓名:___________ 得分:___________
一.选择题:(每小题3分,共36分)
1.下列说法正确的是( )
A.点P(0,5)在x轴上
B.点A(﹣3,4)与点B(3,﹣4)在x轴的同一侧
C.点M(﹣a,a)在第二象限
D.坐标平面内的点与有序数对是一一对应的
2.若P(m,n)与Q(n,m)表示同一个点,那么这个点一定在( )
A.第二、四象限 B.第一、三象限
C.平行于x轴的直线上 D.平行于y轴的直线上
3.如果P点关于x轴的对称点是P′(﹣4,3),那么P点关于y轴的对称点是( )
A.(﹣4,﹣3) B.(4,﹣3) C.(﹣4,3) D.(4,3)
4.把点A(2,﹣3)平移后得到点B(﹣2,3),则平移的过程是( )
A.先向左平移4个单位长度,在向下平移6个单位长度
B.先向左平移4个单位长度,再向上平移6个单位长度
C.先向右平移4个单位长度,在向下平移6个单位长度
D.先向右平移4个单位长度,在向上平移6个单位长度
5.在平面直角坐标系中,点A(2,﹣8)关于原点对称的点的坐标是( )
A.(﹣2,﹣8) B.(﹣2,8) C.(2,8) D.(﹣8,2)
6.Q点(x,y),P点(x,m)是不同的点,则这两点在( )
A.平行于x轴的直线上
B.平行于y轴的直线上
C.第一,第三象限的角平分线上
D.第二,第四象限的角平分线上
7.已知甲、乙两人的身份证号码分别为350500196407280028、350500196807280058,下列信息错误的是( )21*cnjy*com
A.甲、乙同一天出生 B.甲、乙同一天过生日
C.甲、乙异性 D.甲比乙大4岁
8.若图形上一点R(3,﹣4)经过平移后变为R′(﹣2,﹣1),则原图形上另一点S(﹣1,1)平移后的对应点S′的坐标为( )
A.(﹣6,4) B.(4,﹣2) C.(2,﹣4) D.(﹣4,6)
9.△ABC中,A(﹣2,﹣3)、B(﹣1,﹣1)、C(0,1),将△ABC绕B点顺时针旋转90度,则点A对应的点A′的坐标为( )
A.(﹣3,0) B.(3,1) C.(4,1) D.(4,0)
10.如图,Rt△ABC的边AB在x轴上,且A(﹣1,0),B(1,0),∠A=45°,斜边AC以点A为旋转中心,顺时针旋转45°,恰好与x轴相交于D,则点D的坐标是( )
A.(,0) B.(2,0) C.(2﹣1,0) D.(2﹣2,0)
11.如果对某小区参加晨练的人的楼号和门号用有序数对来表示,规定楼号在前,门号在后,在所调查的6个人中,表示的有序数对如下:(9,8),(8,9),(9,7),(7,8),(10,7),(9,10).则这6个人中住在( )号楼的人最多.2·1·c·n·j·y
A.7 B.8 C.9 D.10
12.若A(a,b),B(b,a)表示同一点,那么这一点在( )
A.第二、四象限内两坐标轴夹角平分线上
B.第一象限内两坐标轴夹角平分线上
C.第一、三象限内两坐标轴夹角平分线上
D.平行于y轴的直线上
二.填空题:(每小题3分,共12分)
13.在平面直角坐标系中,P点关于x轴的对称点在第二象限,则P点应在第 象限.
14.已知平面直角坐标系中点B的坐标是(x,y),且xy<0,则点B在第 象限.
15.将点M(a,b)向左平移2个单位长度,再向下平移3个单位长度后,其坐标变为(1,﹣6),则a= ,b= .
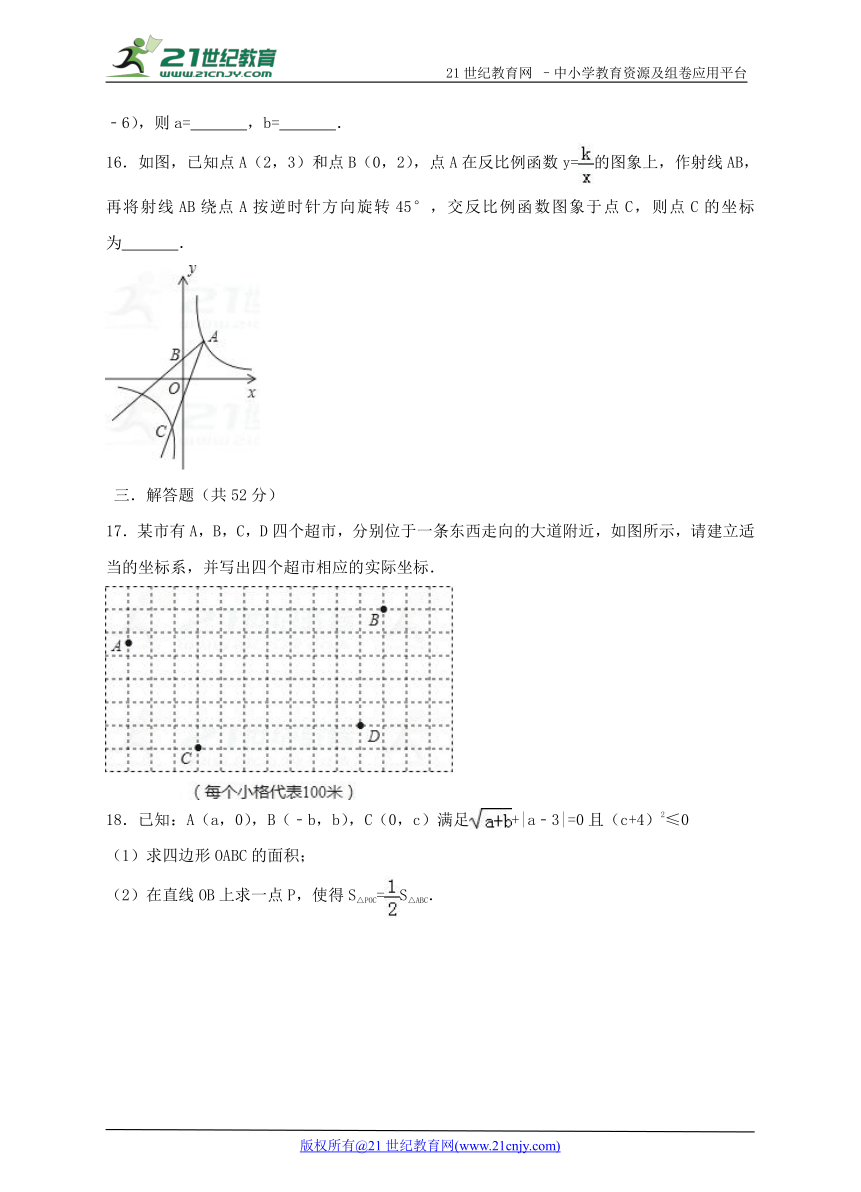
16.如图,已知点A(2,3)和点B(0,2),点A在反比例函数y=的图象上,作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为 .
三.解答题(共52分)
17.某市有A,B,C,D四个超市,分别位于一条东西走向的大道附近,如图所示,请建立适当的坐标系,并写出四个超市相应的实际坐标.21cnjy.com
18.已知:A(a,0),B(﹣b,b),C(0,c)满足+|a﹣3|=0且(c+4)2≤0
(1)求四边形OABC的面积;
(2)在直线OB上求一点P,使得S△POC=S△ABC.
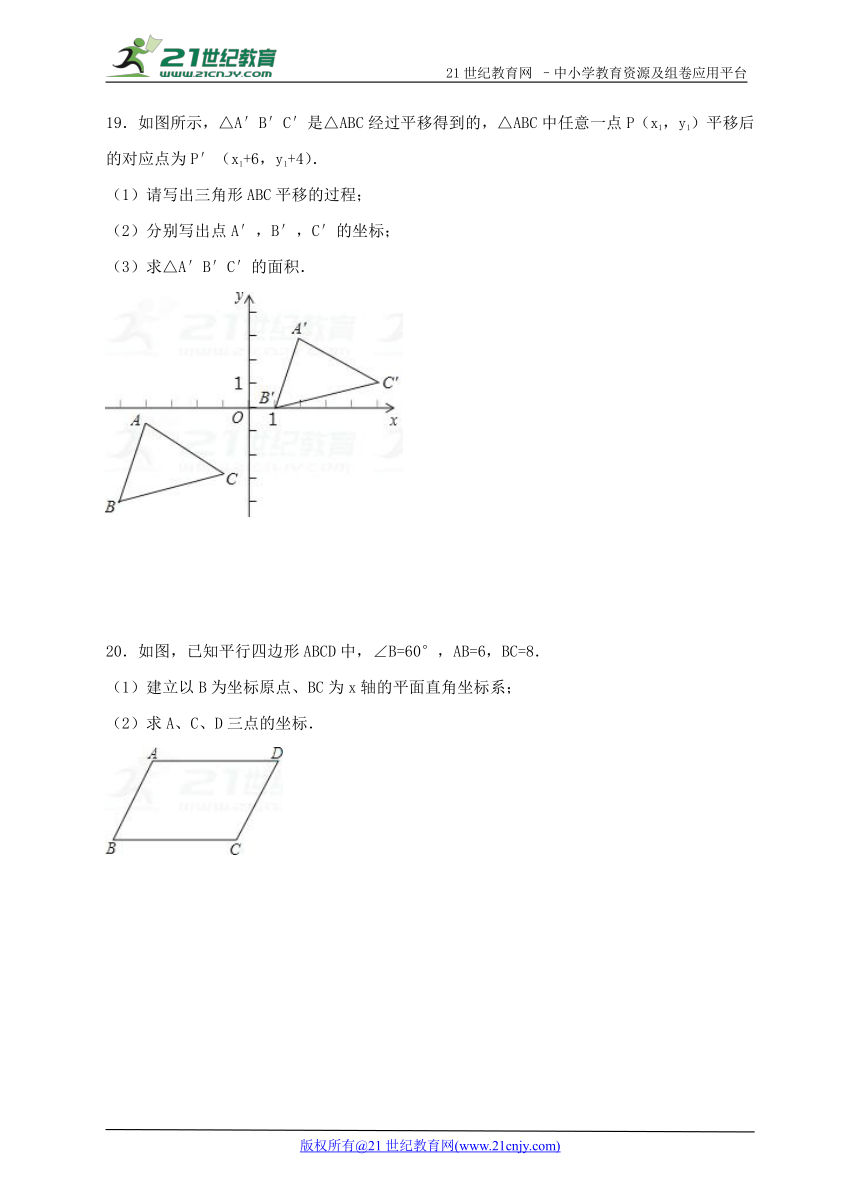
19.如图所示,△A′B′C′是△ABC经过平移得到的,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).
(1)请写出三角形ABC平移的过程;
(2)分别写出点A′,B′,C′的坐标;
(3)求△A′B′C′的面积.
20.如图,已知平行四边形ABCD中,∠B=60°,AB=6,BC=8.
(1)建立以B为坐标原点、BC为x轴的平面直角坐标系;
(2)求A、C、D三点的坐标.
21.在如图所示的图形中,请你建立适当的平面直角坐标系,并写出图中五个景点的坐标.
22.如图,在平面直角坐标系中,已知S△ABO=8,OA=OB,BC=12,点P的坐标是(a,6).
(1)求△ABC三个顶点的坐标;
(2)连接PA、PB,并用含字母a的式子表示△PAB的面积;
(3)是否存在点P,使△PAB的面积等于△ABC的面积?如果存在,求出点P的坐标.
23.在平面直角坐标系中,点A(x,y),点A′(x′,y′),若x′=x+m,y′=y+n,即点A′(x+m,y+n),则表示点A到点A′的一个平移.例如:点A(x,y),点A′(x′,y′),若x′=x+1,y′=y﹣2,则表示A向右平移1个单位,再向下平移2个单位得到点A′.
根据上述定义,探究下列问题:
(1)已知点A(x,y),A′(x﹣3,y),则线段AA′的长度是 ;
(2)已知点A(x,y),A′(x+2,y﹣1),则线段AA′的长度是 ;
(3)矩形AOCB在平面直角坐标系中如图所示,A(0,2),C(4,0),点A′(x′,y′),若x′=x+m,y′=y﹣2m(m,n均为正数),且点A′(x′,y′)在△OCB中(包括三角形的边),求m的取值范围.21·cn·jy·com
答案与解析
一.选择题:(每小题3分,共36分)
1.分析:根据y轴上点的坐标特点对A进行判断;根据各象限点的坐标特点对B进行判断;只有a>0时,M(﹣a,a)在第二象限,由此可对C进行判断;根据直角坐标系中点与有序实数对一一对应对D进行判断.【来源:21·世纪·教育·网】
解答:解:A、点P(0,5)在y轴上,所以A选项错误;
B、点A(﹣3,4)在第二象限,点B(3,﹣4)在第四象限,所以B选项错误;
C、当a>0时,M(﹣a,a)在第二象限,所以C选项错误;
D、坐标平面内的点与有序数对是一一对应的,所以D选项正确.
故选D.
2.分析:让两点的横坐标相等,得到相关式子,把一个点的坐标表示为一个字母表示的坐标,判断即可.
解答:解:∵P(m,n)与Q(n,m)表示同一个点,
∴m=n,
∴P点坐标可表示为(m,m),
∴此点应在第一、三象限,
故选B.
3.分析:根据“关于x轴对称的点,横坐标相同,纵坐标互为相反数”求出点P的坐标,再根据“关于y轴对称的点,纵坐标相同,横坐标互为相反数”解答.21*cnjy*com
解答:解:∵P点关于x轴的对称点是P′(﹣4,3),
∴点P为(﹣4,﹣3),
∴P点关于y轴的对称点是(4,﹣3).
故选B.
4.分析:让新点的横坐标减去原来点的横坐标,若是负数,则是向左平移负数的绝对值单位;反之,则是向右平移正数的单位;
新点的纵坐标减去原来点的纵坐标,若是负数,则是向下平移负数的绝对值单位;反之,则是向上平移正数的单位.
解答:解:∵横坐标的变化为:﹣2﹣2=﹣4,
纵坐标的变化为:3﹣(﹣3)=6.
∴平移过程是向左平移4个单位长度,再向上平移6个单位长度.
故选B.
5.分析:根据点A和点B关于原点对称可知,B点的坐标与A点的坐标互为相反数.
解答:解:∵点A(2,﹣8)与B关于原点对称,
∴B点横坐标﹣2,纵坐标为8,
故选B.
6.分析:根据Q点和P点的横坐标相等,纵坐标不等,可判断Q点和P点在平行于y轴的直线上.
解答:解:∵Q点(x,y),P点(x,m)是不同的点,
∴Q点和P点的横坐标相等,纵坐标不等,
∴Q点和P点在平行于y轴的直线上.
故选B.
7.分析:根据省份证号码可知甲、乙两人的出生年月日,分别判断即可得出答案.
解答:解:∵甲、乙两人的身份证号码分别为350500196407280028、350500196807280058,
∴甲、乙同一天生日,但不是同一天出生,
故甲、乙同一天出生错误,故此选错误.
故选:A.
8.分析:先根据R、R′确定出平移规律,然后列式计算即可求出S′.
解答:解:∵点R(3,﹣4)经过平移后变为R′(﹣2,﹣1),
∴平移规律为向左平移5个单位,向上平移3个单位,
∴﹣1﹣5=﹣6,
1+3=4,
∴点S′的坐标为(﹣6,4).
故选A.
9.分析:根据旋转中心为点B,旋转方向顺时针,旋转角度90°,作出点A的对称图形A′,可得所求点的坐标.www.21-cn-jy.com
解答:解:由图中可以看出点A′的坐标为(﹣3,0),故选A.
10.分析:由AB=2、∠BAC=45°知AC=AD==2,根据OD=AD﹣AO=2﹣1可得答案.2-1-c-n-j-y
解答:解:由题意知,AB=2、∠BAC=45°,
∴AC=AD===2,
则OD=AD﹣AO=2﹣1,
即点D的坐标为(2﹣1,0),
故选:C.
11.分析:找到横坐标相同的最多的个数即可.
解答:解:∵楼号在前,门号在后,
∴9号楼的有:(9,8),(9,7),(9,10)三个,最多.
故选C.
12.分析:根据横纵坐标角平分线上点的坐标特点解答即可.
解答:解:∵A(a,b),B(b,a)表示同一点,
∴它们的横纵坐标相等,横纵坐标同为正或同为负;而横纵坐标相等的点在一三象限的内两坐标轴夹角平分线上.21世纪教育网版权所有
故选.
二.填空题(共4小题)
13.分析:根据平面直角坐标系的特点解答.
解答:解:∵P点关于x轴的对称点在第二象限,
∴点P在第三象限.
故答案为:三.
14.分析:由于xy<0得到x>0,y<0或x<0,y>0,即点(x,y)的横、纵坐标的符号相反,然后根据各象限点的坐标特点进行判断.www-2-1-cnjy-com
解答:解:∵xy<0,
∴x>0,y<0或x<0,y>0,
∴点(x,y)在第二象限或第四象限.
故答案为二或四.
15.分析:所求点的坐标应把所给点向右平移2个单位长度,再向上平移3个单位长度得到.
解答:解:∵点M(a,b)向左平移2个单位长度,再向下平移3个单位长度后,其坐标变为(1,﹣6),
∴a=1+2=3;b=﹣6+3=﹣3.故答案填:3、﹣3.
16.分析:解法1:将点A绕着点B顺时针旋转90°得到点D,连接AD,则△ABD是等腰直角三角形,进而得到点D在射线AC上,根据点A(2,3)和点B(0,2),可得D(1,0),再根据待定系数法求得直线AC的解析式,最后解方程组即可得到点C的坐标;
解法2:先过A作AE⊥x轴于E,以AE为边在AE的左侧作正方形AEFG,交AB于P,根据直线AB的解析式为y=x+2,可得PF=,将△AGP绕点A逆时针旋转90°得△AEH,构造△ADP≌△ADH,再设DE=x,则DH=DP=x+,FD=1+2﹣x=3﹣x,在Rt△PDF中,根据PF2+DF2=PD2,可得方程()2+(3﹣x)2=(x+)2,进而得到D(1,0),即可得出直线AD的解析式为y=3x﹣3,最后解方程组即可得到D点坐标.【出处:21教育名师】
解答:解法1:如图所示,将点A绕着点B顺时针旋转90°得到点D,连接AD,则△ABD是等腰直角三角形,
∴∠BAD=45°,
由题可得,∠BAC=45°,
∴点D在射线AC上,
由点A(2,3)和点B(0,2),可得D(1,0),
设AC的解析式为y=ax+b,
把A(2,3),D(1,0)代入,可得
,解得,
∴直线AC的解析式为y=3x﹣3,
解方程组,可得或,
∴C(﹣1,﹣6),
故答案为:(﹣1,﹣6).
解法2:如图所示,过A作AE⊥x轴于E,以AE为边在AE的左侧作正方形AEFG,交AB于P,
根据点A(2,3)和点B(0,2),可得直线AB的解析式为y=x+2,
由A(2,3),可得OF=1,
当x=﹣1时,y=﹣+2=,即P(﹣1,),
∴PF=,
将△AGP绕点A逆时针旋转90°得△AEH,则△ADP≌△ADH,
∴PD=HD,PG=EH=,
设DE=x,则DH=DP=x+,FD=1+2﹣x=3﹣x,
Rt△PDF中,PF2+DF2=PD2,
即()2+(3﹣x)2=(x+)2,
解得x=1,
∴OD=2﹣1=1,即D(1,0),
根据点A(2,3)和点D(1,0),可得直线AD的解析式为y=3x﹣3,
解方程组,可得或,
∴C(﹣1,﹣6),
故答案为:(﹣1,﹣6).
三.解答题(共7小题)
17.分析:以点C为坐标原点建立平面直角坐标系,然后分别写出各点的坐标即可.
解答:解:建立平面直角坐标系如图所示;
A(300,450),B(800,600),C(0,0),D(700,100).
18.分析:(1)根据已知和偶次方、绝对值、二次根式非负性,求出a、b、c值,进而求得A、B、C坐标,通过观察可以发现四边形OABC为直角梯形,利用梯形面积公式求出四边形OABC面积;21·世纪*教育网
(2)首先求出三角形ABC面积,进而知道三角形POC面积,求出点P的横坐标,利用点B求直线OB直线解析式,将点P坐标代入直线OB即可求出点P坐标.21教育名师原创作品
解答:解:(1)∵+|a﹣3|=0且(c+4)2≤0,
∴=0,|a﹣3|=0且(c+4)2=0,
∴a=3,b=﹣3,c=﹣4,
∴A(3,0),B(3,﹣3),C(0,﹣4),
由点的特征知四边形OABC为直角梯形,
∴S四边形OABC=×(OC+AB)×OA,
=×(4+3)×3,
=.
答:四边形OABC的面积为.
(2)S△ABC=×AB×3=×3×3=,
∴S△ABC=,
S△POC=,
设P(x,y)
即:×OC×|x|=,
∴×4×|x|=,
解得x=±,
∴P(±,y)
设直线OB为y=kx,(k≠0),
将点B(3,﹣3)代入,
得k=﹣1,
∴直线OB解析式为:y=﹣x,
将点P代入得:
P(,﹣)或P(﹣,).
19.分析:(1)由平移前后的一对对应点P与P′的坐标,可知横坐标加6,纵坐标加4,根据点的平移规律:右加左减、上加下减,即可求解;21教育网
(2)根据图形直接写出点A′,B′,C′的坐标;
(3)利用△A′B′C′所在的矩形的面积减去四周三个小直角三角形的面积,列式进行计算即可得解.
解答:解:(1)∵△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4),
∴平移前后对应点的横坐标加6,纵坐标加4,
∴△ABC先向右平移6个单位,再向上平移4个单位得到△A′B′C′或△ABC先向上平移4个单位,再向右平移6个单位得到△A′B′C′;
(2)A′(2,3),B′(1,0),C′(5,1);
(3)S△A′B′C′=4×3﹣×3×1﹣×3×2﹣×1×4
=12﹣1.5﹣3﹣2
=5.5.
20.分析:(1)根据题意建立直角坐标系;
(2)过A作AE⊥BC于E,然后求出BE、AE的长,写出点A的坐标,再根据BC的长度写出点C的坐标,求出点D的横坐标,然后写出点D的坐标.
解答:解:(1)如右图建立直角坐标系;
(2)过A作AE⊥BC于E,
∵∠B=60°,AB=6,
∴∠BAE=30°,BE=AB=3,AE===3,
∴A点坐标为(3,3),
∵BC=8,
∴C点坐标为(8,0),
∵AD∥BC,且AD=BC=8,
∴D点坐标为(11,3).
21.分析:建立如图所示的直角坐标系,然后根据各象限和坐标轴上点的坐标特征求解.
解答:解:建立如图所示的直角坐标系,
文庙的坐标为(0,2),开遥县衙的坐标为(﹣2,0),古城墙的坐标为(﹣3,3),日升昌的坐标为(5,﹣1),双林寺的坐标为(9,﹣2).
22.分析:(1)根据三角形面积公式得到 OA2=8,解得OA=4,则OB=OA=4,OC=BC﹣OB=8,然后根据坐标轴上点的坐标特征写出△ABC三个顶点的坐标;【来源:21cnj*y.co*m】
(2)分类讨论:当点P在第一象限,当a>2时,S△PAB=S△AOB+S梯形AOHP﹣S△PBH=2a﹣4;当0<a<2时,S△PAB=S△PBH﹣S梯形AOHP﹣S△AOB=﹣2a+4;
当点P在第二象限,即a<0,作PH⊥y轴于H,如图2,利用S△PAB=S梯形OHPB﹣S△PAH﹣S△OAB求解;
(3)先计算出S△ABC=24,再根据(2)中的分类得到2a﹣4=24或4﹣2a=24,然后分别求出a的值,从而确定P点坐标.
解答:解:(1)∵S△ABO= OA OB,
而OA=OB,
∴ OA2=8,解得OA=4,
∴OB=OA=4,
∴OC=BC﹣OB=12﹣4=8,
∴A(0,4),B(﹣4,0),C(8,0);
(2)当点P在第一象限,即a>0,作PH⊥x轴于H,如图1,
当a>2时,S△PAB=S△AOB+S梯形AOHP﹣S△PBH=8+ a﹣ 6 (a+4)=2a﹣4;
当0<a<2时,S△PAB=S△PBH﹣S梯形AOHP﹣S△AOB= 6 (a+4)﹣8﹣(4+6)a=﹣2a+4;
当点P在第二象限,即a<0,作PH⊥y轴于H,如图2,
S△PAB=S梯形OHPB﹣S△PAH﹣S△OAB= 6﹣ (6﹣4) a﹣8=4﹣2a;
(3)存在.
S△ABC= 4 12=24,
当P(a,6)在第一象限,则2a﹣4=24,解得a=14,此时P点坐标为(14,6);或﹣2a+4=24,解得a=﹣10(舍去);【版权所有:21教育】
当P(a,6)在第二象限,则4﹣2a=24,解得a=﹣10,此时P点坐标为(﹣10,6),
综上所述,点P的坐标为(﹣10,6)或(14,6).
23.分析:(1)由点A(x,y),A′(x﹣3,y),则点A向左平移3个单位得到点A′,所以线段AA′的长度是3;
(2)由点A(x,y),A′(x+2,y﹣1),则点A向右平移2个单位,再向下平移1个单位得到点A′,根据勾股定理即可求出线段AA′的长度;
(3)由tan∠BOC===可知,如果点A′(x′,y′)在△OCB中(包括三角形的边),那么y′≤x′,即2﹣2m≤m,解得m≥,再根据0≤
x′≤4即可求解.
解答:解:(1)已知点A(x,y),A′(x﹣3,y),则线段AA′的长度是3;
(2)已知点A(x,y),A′(x+2,y﹣1),则线段AA′的长度是=;
(3)∵A(0,2),点A′(x′,y′),
∴x′=x+m=m,y′=y﹣2m=2﹣2m.
∵tan∠BOC===,
∴当点A′(x′,y′)在△OCB中(包括三角形的边)时,y′≤x′,
即2﹣2m≤m,
解得m≥,
又0≤m≤4,
∴≤m≤4.
故答案为3;.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
【新北师大版八年级数学(上)单元测试卷】
第三章《位置与坐标》(含答案与解析)
班级:___________ 姓名:___________ 得分:___________
一.选择题:(每小题3分,共36分)
1.下列说法正确的是( )
A.点P(0,5)在x轴上
B.点A(﹣3,4)与点B(3,﹣4)在x轴的同一侧
C.点M(﹣a,a)在第二象限
D.坐标平面内的点与有序数对是一一对应的
2.若P(m,n)与Q(n,m)表示同一个点,那么这个点一定在( )
A.第二、四象限 B.第一、三象限
C.平行于x轴的直线上 D.平行于y轴的直线上
3.如果P点关于x轴的对称点是P′(﹣4,3),那么P点关于y轴的对称点是( )
A.(﹣4,﹣3) B.(4,﹣3) C.(﹣4,3) D.(4,3)
4.把点A(2,﹣3)平移后得到点B(﹣2,3),则平移的过程是( )
A.先向左平移4个单位长度,在向下平移6个单位长度
B.先向左平移4个单位长度,再向上平移6个单位长度
C.先向右平移4个单位长度,在向下平移6个单位长度
D.先向右平移4个单位长度,在向上平移6个单位长度
5.在平面直角坐标系中,点A(2,﹣8)关于原点对称的点的坐标是( )
A.(﹣2,﹣8) B.(﹣2,8) C.(2,8) D.(﹣8,2)
6.Q点(x,y),P点(x,m)是不同的点,则这两点在( )
A.平行于x轴的直线上
B.平行于y轴的直线上
C.第一,第三象限的角平分线上
D.第二,第四象限的角平分线上
7.已知甲、乙两人的身份证号码分别为350500196407280028、350500196807280058,下列信息错误的是( )21*cnjy*com
A.甲、乙同一天出生 B.甲、乙同一天过生日
C.甲、乙异性 D.甲比乙大4岁
8.若图形上一点R(3,﹣4)经过平移后变为R′(﹣2,﹣1),则原图形上另一点S(﹣1,1)平移后的对应点S′的坐标为( )
A.(﹣6,4) B.(4,﹣2) C.(2,﹣4) D.(﹣4,6)
9.△ABC中,A(﹣2,﹣3)、B(﹣1,﹣1)、C(0,1),将△ABC绕B点顺时针旋转90度,则点A对应的点A′的坐标为( )
A.(﹣3,0) B.(3,1) C.(4,1) D.(4,0)
10.如图,Rt△ABC的边AB在x轴上,且A(﹣1,0),B(1,0),∠A=45°,斜边AC以点A为旋转中心,顺时针旋转45°,恰好与x轴相交于D,则点D的坐标是( )
A.(,0) B.(2,0) C.(2﹣1,0) D.(2﹣2,0)
11.如果对某小区参加晨练的人的楼号和门号用有序数对来表示,规定楼号在前,门号在后,在所调查的6个人中,表示的有序数对如下:(9,8),(8,9),(9,7),(7,8),(10,7),(9,10).则这6个人中住在( )号楼的人最多.2·1·c·n·j·y
A.7 B.8 C.9 D.10
12.若A(a,b),B(b,a)表示同一点,那么这一点在( )
A.第二、四象限内两坐标轴夹角平分线上
B.第一象限内两坐标轴夹角平分线上
C.第一、三象限内两坐标轴夹角平分线上
D.平行于y轴的直线上
二.填空题:(每小题3分,共12分)
13.在平面直角坐标系中,P点关于x轴的对称点在第二象限,则P点应在第 象限.
14.已知平面直角坐标系中点B的坐标是(x,y),且xy<0,则点B在第 象限.
15.将点M(a,b)向左平移2个单位长度,再向下平移3个单位长度后,其坐标变为(1,﹣6),则a= ,b= .
16.如图,已知点A(2,3)和点B(0,2),点A在反比例函数y=的图象上,作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为 .
三.解答题(共52分)
17.某市有A,B,C,D四个超市,分别位于一条东西走向的大道附近,如图所示,请建立适当的坐标系,并写出四个超市相应的实际坐标.21cnjy.com
18.已知:A(a,0),B(﹣b,b),C(0,c)满足+|a﹣3|=0且(c+4)2≤0
(1)求四边形OABC的面积;
(2)在直线OB上求一点P,使得S△POC=S△ABC.
19.如图所示,△A′B′C′是△ABC经过平移得到的,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).
(1)请写出三角形ABC平移的过程;
(2)分别写出点A′,B′,C′的坐标;
(3)求△A′B′C′的面积.
20.如图,已知平行四边形ABCD中,∠B=60°,AB=6,BC=8.
(1)建立以B为坐标原点、BC为x轴的平面直角坐标系;
(2)求A、C、D三点的坐标.
21.在如图所示的图形中,请你建立适当的平面直角坐标系,并写出图中五个景点的坐标.
22.如图,在平面直角坐标系中,已知S△ABO=8,OA=OB,BC=12,点P的坐标是(a,6).
(1)求△ABC三个顶点的坐标;
(2)连接PA、PB,并用含字母a的式子表示△PAB的面积;
(3)是否存在点P,使△PAB的面积等于△ABC的面积?如果存在,求出点P的坐标.
23.在平面直角坐标系中,点A(x,y),点A′(x′,y′),若x′=x+m,y′=y+n,即点A′(x+m,y+n),则表示点A到点A′的一个平移.例如:点A(x,y),点A′(x′,y′),若x′=x+1,y′=y﹣2,则表示A向右平移1个单位,再向下平移2个单位得到点A′.
根据上述定义,探究下列问题:
(1)已知点A(x,y),A′(x﹣3,y),则线段AA′的长度是 ;
(2)已知点A(x,y),A′(x+2,y﹣1),则线段AA′的长度是 ;
(3)矩形AOCB在平面直角坐标系中如图所示,A(0,2),C(4,0),点A′(x′,y′),若x′=x+m,y′=y﹣2m(m,n均为正数),且点A′(x′,y′)在△OCB中(包括三角形的边),求m的取值范围.21·cn·jy·com
答案与解析
一.选择题:(每小题3分,共36分)
1.分析:根据y轴上点的坐标特点对A进行判断;根据各象限点的坐标特点对B进行判断;只有a>0时,M(﹣a,a)在第二象限,由此可对C进行判断;根据直角坐标系中点与有序实数对一一对应对D进行判断.【来源:21·世纪·教育·网】
解答:解:A、点P(0,5)在y轴上,所以A选项错误;
B、点A(﹣3,4)在第二象限,点B(3,﹣4)在第四象限,所以B选项错误;
C、当a>0时,M(﹣a,a)在第二象限,所以C选项错误;
D、坐标平面内的点与有序数对是一一对应的,所以D选项正确.
故选D.
2.分析:让两点的横坐标相等,得到相关式子,把一个点的坐标表示为一个字母表示的坐标,判断即可.
解答:解:∵P(m,n)与Q(n,m)表示同一个点,
∴m=n,
∴P点坐标可表示为(m,m),
∴此点应在第一、三象限,
故选B.
3.分析:根据“关于x轴对称的点,横坐标相同,纵坐标互为相反数”求出点P的坐标,再根据“关于y轴对称的点,纵坐标相同,横坐标互为相反数”解答.21*cnjy*com
解答:解:∵P点关于x轴的对称点是P′(﹣4,3),
∴点P为(﹣4,﹣3),
∴P点关于y轴的对称点是(4,﹣3).
故选B.
4.分析:让新点的横坐标减去原来点的横坐标,若是负数,则是向左平移负数的绝对值单位;反之,则是向右平移正数的单位;
新点的纵坐标减去原来点的纵坐标,若是负数,则是向下平移负数的绝对值单位;反之,则是向上平移正数的单位.
解答:解:∵横坐标的变化为:﹣2﹣2=﹣4,
纵坐标的变化为:3﹣(﹣3)=6.
∴平移过程是向左平移4个单位长度,再向上平移6个单位长度.
故选B.
5.分析:根据点A和点B关于原点对称可知,B点的坐标与A点的坐标互为相反数.
解答:解:∵点A(2,﹣8)与B关于原点对称,
∴B点横坐标﹣2,纵坐标为8,
故选B.
6.分析:根据Q点和P点的横坐标相等,纵坐标不等,可判断Q点和P点在平行于y轴的直线上.
解答:解:∵Q点(x,y),P点(x,m)是不同的点,
∴Q点和P点的横坐标相等,纵坐标不等,
∴Q点和P点在平行于y轴的直线上.
故选B.
7.分析:根据省份证号码可知甲、乙两人的出生年月日,分别判断即可得出答案.
解答:解:∵甲、乙两人的身份证号码分别为350500196407280028、350500196807280058,
∴甲、乙同一天生日,但不是同一天出生,
故甲、乙同一天出生错误,故此选错误.
故选:A.
8.分析:先根据R、R′确定出平移规律,然后列式计算即可求出S′.
解答:解:∵点R(3,﹣4)经过平移后变为R′(﹣2,﹣1),
∴平移规律为向左平移5个单位,向上平移3个单位,
∴﹣1﹣5=﹣6,
1+3=4,
∴点S′的坐标为(﹣6,4).
故选A.
9.分析:根据旋转中心为点B,旋转方向顺时针,旋转角度90°,作出点A的对称图形A′,可得所求点的坐标.www.21-cn-jy.com
解答:解:由图中可以看出点A′的坐标为(﹣3,0),故选A.
10.分析:由AB=2、∠BAC=45°知AC=AD==2,根据OD=AD﹣AO=2﹣1可得答案.2-1-c-n-j-y
解答:解:由题意知,AB=2、∠BAC=45°,
∴AC=AD===2,
则OD=AD﹣AO=2﹣1,
即点D的坐标为(2﹣1,0),
故选:C.
11.分析:找到横坐标相同的最多的个数即可.
解答:解:∵楼号在前,门号在后,
∴9号楼的有:(9,8),(9,7),(9,10)三个,最多.
故选C.
12.分析:根据横纵坐标角平分线上点的坐标特点解答即可.
解答:解:∵A(a,b),B(b,a)表示同一点,
∴它们的横纵坐标相等,横纵坐标同为正或同为负;而横纵坐标相等的点在一三象限的内两坐标轴夹角平分线上.21世纪教育网版权所有
故选.
二.填空题(共4小题)
13.分析:根据平面直角坐标系的特点解答.
解答:解:∵P点关于x轴的对称点在第二象限,
∴点P在第三象限.
故答案为:三.
14.分析:由于xy<0得到x>0,y<0或x<0,y>0,即点(x,y)的横、纵坐标的符号相反,然后根据各象限点的坐标特点进行判断.www-2-1-cnjy-com
解答:解:∵xy<0,
∴x>0,y<0或x<0,y>0,
∴点(x,y)在第二象限或第四象限.
故答案为二或四.
15.分析:所求点的坐标应把所给点向右平移2个单位长度,再向上平移3个单位长度得到.
解答:解:∵点M(a,b)向左平移2个单位长度,再向下平移3个单位长度后,其坐标变为(1,﹣6),
∴a=1+2=3;b=﹣6+3=﹣3.故答案填:3、﹣3.
16.分析:解法1:将点A绕着点B顺时针旋转90°得到点D,连接AD,则△ABD是等腰直角三角形,进而得到点D在射线AC上,根据点A(2,3)和点B(0,2),可得D(1,0),再根据待定系数法求得直线AC的解析式,最后解方程组即可得到点C的坐标;
解法2:先过A作AE⊥x轴于E,以AE为边在AE的左侧作正方形AEFG,交AB于P,根据直线AB的解析式为y=x+2,可得PF=,将△AGP绕点A逆时针旋转90°得△AEH,构造△ADP≌△ADH,再设DE=x,则DH=DP=x+,FD=1+2﹣x=3﹣x,在Rt△PDF中,根据PF2+DF2=PD2,可得方程()2+(3﹣x)2=(x+)2,进而得到D(1,0),即可得出直线AD的解析式为y=3x﹣3,最后解方程组即可得到D点坐标.【出处:21教育名师】
解答:解法1:如图所示,将点A绕着点B顺时针旋转90°得到点D,连接AD,则△ABD是等腰直角三角形,
∴∠BAD=45°,
由题可得,∠BAC=45°,
∴点D在射线AC上,
由点A(2,3)和点B(0,2),可得D(1,0),
设AC的解析式为y=ax+b,
把A(2,3),D(1,0)代入,可得
,解得,
∴直线AC的解析式为y=3x﹣3,
解方程组,可得或,
∴C(﹣1,﹣6),
故答案为:(﹣1,﹣6).
解法2:如图所示,过A作AE⊥x轴于E,以AE为边在AE的左侧作正方形AEFG,交AB于P,
根据点A(2,3)和点B(0,2),可得直线AB的解析式为y=x+2,
由A(2,3),可得OF=1,
当x=﹣1时,y=﹣+2=,即P(﹣1,),
∴PF=,
将△AGP绕点A逆时针旋转90°得△AEH,则△ADP≌△ADH,
∴PD=HD,PG=EH=,
设DE=x,则DH=DP=x+,FD=1+2﹣x=3﹣x,
Rt△PDF中,PF2+DF2=PD2,
即()2+(3﹣x)2=(x+)2,
解得x=1,
∴OD=2﹣1=1,即D(1,0),
根据点A(2,3)和点D(1,0),可得直线AD的解析式为y=3x﹣3,
解方程组,可得或,
∴C(﹣1,﹣6),
故答案为:(﹣1,﹣6).
三.解答题(共7小题)
17.分析:以点C为坐标原点建立平面直角坐标系,然后分别写出各点的坐标即可.
解答:解:建立平面直角坐标系如图所示;
A(300,450),B(800,600),C(0,0),D(700,100).
18.分析:(1)根据已知和偶次方、绝对值、二次根式非负性,求出a、b、c值,进而求得A、B、C坐标,通过观察可以发现四边形OABC为直角梯形,利用梯形面积公式求出四边形OABC面积;21·世纪*教育网
(2)首先求出三角形ABC面积,进而知道三角形POC面积,求出点P的横坐标,利用点B求直线OB直线解析式,将点P坐标代入直线OB即可求出点P坐标.21教育名师原创作品
解答:解:(1)∵+|a﹣3|=0且(c+4)2≤0,
∴=0,|a﹣3|=0且(c+4)2=0,
∴a=3,b=﹣3,c=﹣4,
∴A(3,0),B(3,﹣3),C(0,﹣4),
由点的特征知四边形OABC为直角梯形,
∴S四边形OABC=×(OC+AB)×OA,
=×(4+3)×3,
=.
答:四边形OABC的面积为.
(2)S△ABC=×AB×3=×3×3=,
∴S△ABC=,
S△POC=,
设P(x,y)
即:×OC×|x|=,
∴×4×|x|=,
解得x=±,
∴P(±,y)
设直线OB为y=kx,(k≠0),
将点B(3,﹣3)代入,
得k=﹣1,
∴直线OB解析式为:y=﹣x,
将点P代入得:
P(,﹣)或P(﹣,).
19.分析:(1)由平移前后的一对对应点P与P′的坐标,可知横坐标加6,纵坐标加4,根据点的平移规律:右加左减、上加下减,即可求解;21教育网
(2)根据图形直接写出点A′,B′,C′的坐标;
(3)利用△A′B′C′所在的矩形的面积减去四周三个小直角三角形的面积,列式进行计算即可得解.
解答:解:(1)∵△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4),
∴平移前后对应点的横坐标加6,纵坐标加4,
∴△ABC先向右平移6个单位,再向上平移4个单位得到△A′B′C′或△ABC先向上平移4个单位,再向右平移6个单位得到△A′B′C′;
(2)A′(2,3),B′(1,0),C′(5,1);
(3)S△A′B′C′=4×3﹣×3×1﹣×3×2﹣×1×4
=12﹣1.5﹣3﹣2
=5.5.
20.分析:(1)根据题意建立直角坐标系;
(2)过A作AE⊥BC于E,然后求出BE、AE的长,写出点A的坐标,再根据BC的长度写出点C的坐标,求出点D的横坐标,然后写出点D的坐标.
解答:解:(1)如右图建立直角坐标系;
(2)过A作AE⊥BC于E,
∵∠B=60°,AB=6,
∴∠BAE=30°,BE=AB=3,AE===3,
∴A点坐标为(3,3),
∵BC=8,
∴C点坐标为(8,0),
∵AD∥BC,且AD=BC=8,
∴D点坐标为(11,3).
21.分析:建立如图所示的直角坐标系,然后根据各象限和坐标轴上点的坐标特征求解.
解答:解:建立如图所示的直角坐标系,
文庙的坐标为(0,2),开遥县衙的坐标为(﹣2,0),古城墙的坐标为(﹣3,3),日升昌的坐标为(5,﹣1),双林寺的坐标为(9,﹣2).
22.分析:(1)根据三角形面积公式得到 OA2=8,解得OA=4,则OB=OA=4,OC=BC﹣OB=8,然后根据坐标轴上点的坐标特征写出△ABC三个顶点的坐标;【来源:21cnj*y.co*m】
(2)分类讨论:当点P在第一象限,当a>2时,S△PAB=S△AOB+S梯形AOHP﹣S△PBH=2a﹣4;当0<a<2时,S△PAB=S△PBH﹣S梯形AOHP﹣S△AOB=﹣2a+4;
当点P在第二象限,即a<0,作PH⊥y轴于H,如图2,利用S△PAB=S梯形OHPB﹣S△PAH﹣S△OAB求解;
(3)先计算出S△ABC=24,再根据(2)中的分类得到2a﹣4=24或4﹣2a=24,然后分别求出a的值,从而确定P点坐标.
解答:解:(1)∵S△ABO= OA OB,
而OA=OB,
∴ OA2=8,解得OA=4,
∴OB=OA=4,
∴OC=BC﹣OB=12﹣4=8,
∴A(0,4),B(﹣4,0),C(8,0);
(2)当点P在第一象限,即a>0,作PH⊥x轴于H,如图1,
当a>2时,S△PAB=S△AOB+S梯形AOHP﹣S△PBH=8+ a﹣ 6 (a+4)=2a﹣4;
当0<a<2时,S△PAB=S△PBH﹣S梯形AOHP﹣S△AOB= 6 (a+4)﹣8﹣(4+6)a=﹣2a+4;
当点P在第二象限,即a<0,作PH⊥y轴于H,如图2,
S△PAB=S梯形OHPB﹣S△PAH﹣S△OAB= 6﹣ (6﹣4) a﹣8=4﹣2a;
(3)存在.
S△ABC= 4 12=24,
当P(a,6)在第一象限,则2a﹣4=24,解得a=14,此时P点坐标为(14,6);或﹣2a+4=24,解得a=﹣10(舍去);【版权所有:21教育】
当P(a,6)在第二象限,则4﹣2a=24,解得a=﹣10,此时P点坐标为(﹣10,6),
综上所述,点P的坐标为(﹣10,6)或(14,6).
23.分析:(1)由点A(x,y),A′(x﹣3,y),则点A向左平移3个单位得到点A′,所以线段AA′的长度是3;
(2)由点A(x,y),A′(x+2,y﹣1),则点A向右平移2个单位,再向下平移1个单位得到点A′,根据勾股定理即可求出线段AA′的长度;
(3)由tan∠BOC===可知,如果点A′(x′,y′)在△OCB中(包括三角形的边),那么y′≤x′,即2﹣2m≤m,解得m≥,再根据0≤
x′≤4即可求解.
解答:解:(1)已知点A(x,y),A′(x﹣3,y),则线段AA′的长度是3;
(2)已知点A(x,y),A′(x+2,y﹣1),则线段AA′的长度是=;
(3)∵A(0,2),点A′(x′,y′),
∴x′=x+m=m,y′=y﹣2m=2﹣2m.
∵tan∠BOC===,
∴当点A′(x′,y′)在△OCB中(包括三角形的边)时,y′≤x′,
即2﹣2m≤m,
解得m≥,
又0≤m≤4,
∴≤m≤4.
故答案为3;.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
