苏科版八年级上第二章《轴对称图形》提优练习(含14课时,含答案)
文档属性
| 名称 | 苏科版八年级上第二章《轴对称图形》提优练习(含14课时,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-25 19:11:11 | ||
图片预览

文档简介
第2章
轴对称图形
第1课时
轴对称与轴对称图形
1.下列图形中,对称轴的数量小于3的是(
)
2.已知各边相等,各角也相等的多边形叫做正多边形,也称为正边形(这里且为整数).如图,请你探究下列正多边形的对称轴的条数,并填在表格中.
正多边形的边教
3
4
5
6
7
8
对称轴的条数
(1)猜想:正边形有
条对称轴;
(2)当越来越大时,正多边形接近于
,该图形有
条对称轴.
3.小明学习了轴对称知识后,忽然想起了参加数学兴趣小组时老师布置的一道题,当时小明没做出来,题目是这样的:有一组数据排列成方阵,如图.试用简便方法计算这组数据的和.小明想:不考虑每个数据的大小,只考虑每个数据的位置,这个图形是个轴对称图形,能不能用轴对称思想来解决这个问题呢 小明顺着这个思路很快解决了这个题目,请你写出他的解题过程.
第2课时
轴对称的性质(1)
1.如图,把一张长方形纸片沿折叠后,点落在边上的点处,点落在点处,若,则的度数为(
)
A.
115°
B.
120°
C.
130°
D.
140°
2.如图,点关于的对称点分别是,分别交于点,=16
cm,则的周长为
cm.
3.如图,为内部一点,
.
(1)分别画出点关于直线的对称点;
(2)请指出当的度数为多少时,=7,并说明理由;
(3)请判断当的度数不是(2)中的度数时,的长度是小于7还是大于7,并说明你的判断的理由.
第3课时
轴对称的性质(2)
1.如图,点在方格纸的格点位置上,若要再找一个格点,使它们所构成的三角形为轴对称图形,则这样的格点在图中共有(
)
A.
4个
B.
6个
C.
8个
D.
10个
2.如图,在2×2的正方形网格纸中,有一个以格点为顶点的.请你找出网格纸中所有与成轴对称且也以格点为顶点的三角形,这样的不角形共有
个.
3.如图,在由边长为1的正方形组成的6×5方格中,点都在格点上.
(1)在给定的方格中将线段平移到,使得四边形是长方形,且点都落在格点上.画出四边形,并叙述线段的平移过程.
(2)在方格中画出关于直线对称的.
(3)求五边形的面积.
第4课时
轴对称的性质—习题课
7.如图,线段在直线的一侧,请在直线上找一点,使的周长最短.画出图形,保留画图痕迹,不写画法.
2.如图,在直线上找一点,使得与直线的夹角相等.画出图形,保留画图痕迹,不写画法.
3.
(1)如图①,
是内一点,在上分别找点,使得的周长最短.画出图形,保留画图痕迹,不写画法.
(2)如图②,
是内的两点,在上分别找点,使得以为顶点的四边形的周长最短.画出图形,保留画图痕迹,不写画法.
第5课时
设计轴对称图案
1.在一次数学活动课上,小颖将一个四边形纸片依次按如图①②所示的方式对折,然后按图③中的虚线裁剪成图④样式,将纸片展开铺平,所得到的图形是(
)
2.在4×4的方格中,有五个同样大小的正方形按如图所示的方式摆放,移动其中一个正方形到空白方格中,与其余四个正方形组成的新图形是一个轴对称图形,这样的移法共有
种.
3.在3×3的正方形网格图中,有格点三角形和格点三角形,且和
关于某条直线成轴对称,请在如图①~⑥所示的网格中画出六个这样的.(每种方案均不相同)
第6课时
线段、角的轴对称性(1)
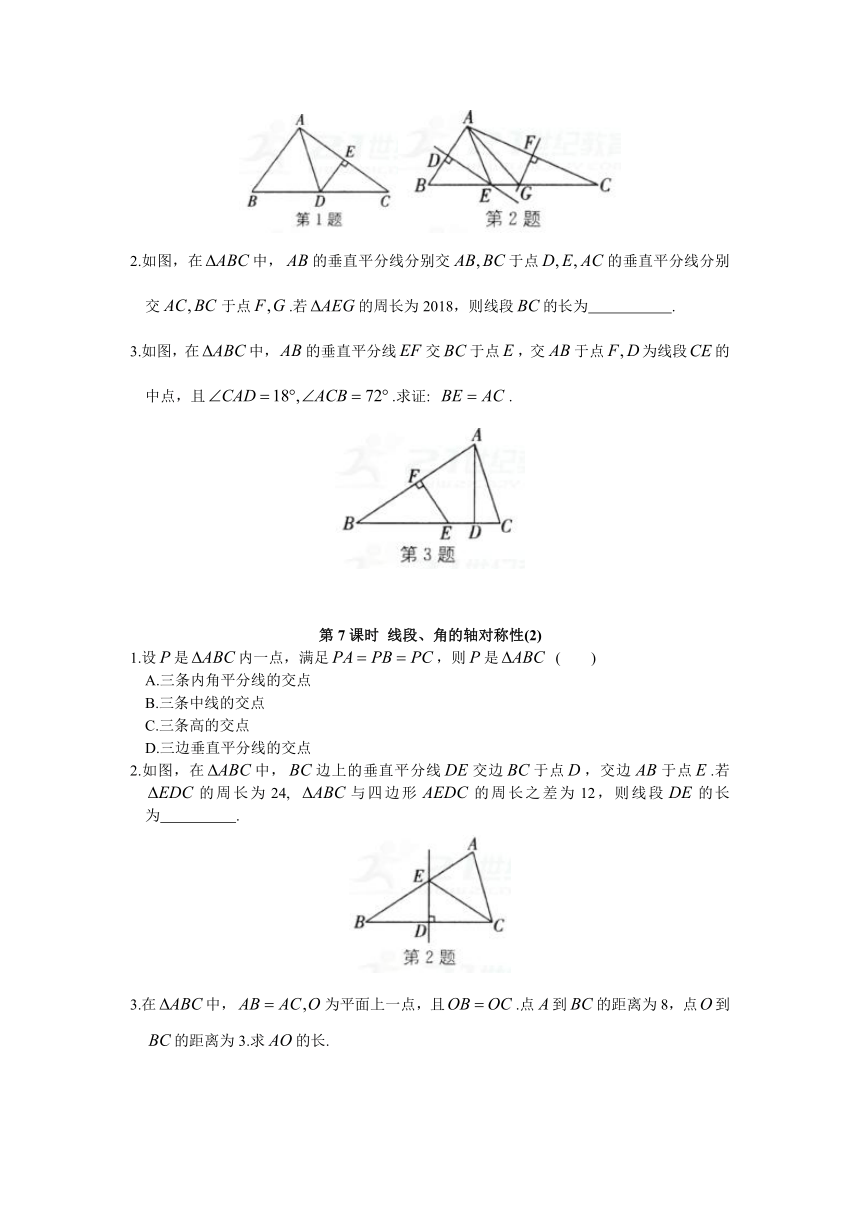
1.如图,在中,的垂直平分线分别交于点=
4
,
的周长为23,则的周长为(
)
A.
13
B.
15
C.
17
D.
19
2.如图,在中,的垂直平分线分别交于点的垂直平分线分别交于点.若的周长为2018,则线段的长为
.
3.如图,在中,的垂直平分线交于点,交于点为线段的中点,且.求证:
.
第7课时
线段、角的轴对称性(2)
1.设是内一点,满足,则是
(
)
A.三条内角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
2.如图,在中,边上的垂直平分线交边于点,交边于点.若的周长为24,
与四边形的周长之差为12,则线段的长为
.
3.在中,为平面上一点,且.点到的距离为8,点到的距离为3.求的长.
第8课时
线段、角的轴对称性(3)
1.如图,的面积为6,=3,现将沿所在直线翻折,使点落在直线
上的点处,为直线上的一点,则线段的长不可能是(
)
A.
3
B.
4
C.
5.
5
D.
10
2.如图,分别平分过点,且与垂直.若=8,则点到的距离为
.
3.如图,为的边的垂直平分线,过点作另外两边所在直线的垂线,垂足分别为,且,作射线.求证:
平分.
第9课时
线段、角的轴对称性(4)
1.如图,的平分线交于点,过点作,垂足分别为.下列结论:①平分;②;③;④.其中正确的是(
)
A.
①②③
B.
①③④
C.
②③④
D.①③
2.如图,是的角平分线,分别是和的高,连接,交
于点.下列结论:①;②;③;④;
⑤垂直平分.其中一定正确的是
.(填序号)
3.如图.在中,,边的垂直平分线交的外角的平分线于点,垂足为,垂足为.求证:
.
第10课时
等腰三角形的轴对称性(1)
1.如图,在中,,分别以点和点为圆心,大于的长为半径画弧,两弧相交于点,作直线,交于点,连接,则的度数为(
)
A.
65°
B.
60°
C.
55°
D.
45°
2.如图,在中,为上一点,为上一点,且,则的度数为
.
3.如图,在中,,
为斜边上的两点,且,求的度数.
第11课时
等腰三角形的轴对称性(1)—习题课
1.已知等腰三角形一腰上的高与另一腰的夹角为60°,则这个等腰三角形的底角的度数为(
)
A.
30°
B.
75°
C.
15°或30°
D.
75°或15°
2.如图,在中,,,在边所在的直线上找一点,使是等腰三角形,此时的度数为
.
3.在中,的垂直平分线与所在的直线相交所成的锐角为40°,求的度数.
第12课时
等腰三角形的轴对称性(2)
1.如图,在中,分别是的平分线,且相交于点,则图中的等腰三角形有(
)
A.
5个
B.
6个
C.
7个
D.
8个
2.在中,,当的度数为
时,为等腰三角形.
3.如图①,在中,的平分线交于点,过点作
交于点.
(1)图中有几个等腰三角形 猜想与之间有怎样的数量关系,并说明理由.
(2)如图②,若,其他条件不变,则图中还有等腰三角形吗 如果有,分别写出来;另外在(1)中与之间的数量关系还存在吗
(3)如图③,若在中,
的平分线与的外角平分线交于点,过点作交于点、交于点.这时图中还有等腰三角形吗 与之间的数量关系又如何 并说明你的理由.
第13课时
等腰三角形的轴对称性(2)—习题课
1.如图,,平分,且
=
2.若点分别在上,且为等边三角形,则满足上述条件的有(
)
A.
1个
B.
2个
C.
3个
D.
3个以上
2.如图,在等边三角形中,相交于点于点,则线段的数量关系为
.
3.如图,为线段上一点,,是等边三角形.相交于点交于点,
交于点,连接.
(1)求证:
;
(2)求的度数;
(3)求证:
.
第14课时
等腰三角形的轴对称性(3)
1.如图,在中,
,垂足分别为.若是的中点,则图中等腰三角形有(
)
A.
1个
B.
3个
C.
4个
D.
5个
2.如图,在四边形中,
,
相交于点分别是的中点.如果,那么的度数为
.
3.如图,在中,,点在边上(不与点重合),
于点,连接为的中点.试猜想与的关系并证明.
第2章
轴对称图形
第1课时
轴对称与轴对称图形
1.D
2.
3
4
5
6
7
8
(1)
(2)圆
无数
3.
从方阵的数据看出,正方形的一条对角线上的数据都是10.若把这条对角线所在的直线作为对称轴,把这个方阵对折,对称轴两侧重合的小正方形内的数据之和都是10,相加后如图所示,这样方阵中的所有数据之和为
第2课时
轴对称的性质(1)
1.A
2.
16
3.
(1)如图,过点画,垂足为,在垂线段的延长线上取一点,使得P,此时点就是点关于直线的对称点,同理画出点.
(2)当时,
理由:如图,连接、
∵点、关于直线对称
∴直线垂直平分
∴,
∵
∴
∴,
同理,
∴
若,则,此时、、三点共线
∴
∴
(3)当时,
理由:∵
∴、、三点不在同一直线上,此时构成
∴.由(2),得
∴
第3课时
轴对称的性质(2)
1.D
2.
5
3.(1)如图,将线段先向右平移1个单位长,再向上平移2个单位长度,得线段(平移过程不唯一).
(2)如图,画点关于直线的对称点,连接、,则即为所求.
(
3)
第4课时
轴对称的性质—习题课
1.
由干线段的长度是固定的,要使的周长最短,只要最短即可.如图,过点作它关于直线的对称点,连接交直线于点,连接、,此时就是周长最短的三角形,∴点即为所求.
2.如图,过点作它关干直线的对称点,连接交直线于点.连接、,此时,∴点即为所求.
3.
(1)如图①,过点分别作关于射线、的对称点、,连接,分别交、于点、,连接、、,此时的周长最短,∴点、和即为所求.
(2)如图②.过点、分别作射线、的对称点、,连接,分别交、于点、,连接、、、,此时四边形的周长最短,∴点、和四边形即为所求.
第5课时
设计轴对称图案
1.A
2.
13
3.要使和于某条直线成轴对称,关键是确定适当的对称轴.再根据轴对称的性质画出符合条件的图案,可以以的正方形网格图的对称轴为对称轴画出所求的,有四个不同位置的三角形;也可以以的边、的中点连线所在的直线为对称轴画出所求的,有一个三角形;还可以把过的顶点与边平行的直线作为对称轴画出所求的,也有一个三角形.如图①~⑥中的即为所求
第6课时
线段、角的轴对称性(1)
1.B
2.
2018
3.
连接,
∵是的垂直平分线
∴
∵在中.,,
∴
即
∵为线段的中点
∴
∴垂直平分
∴
∴
第7课时
线段、角的轴对称性(2)
1.D
2.
6
3.∵
∴点在线段的垂直平分线上
∵
∴点也在线段的垂直平分线上
∴所在的直线即为线段的垂直平分线.
设直线与交于点.由题意,得
如图①.当点、在的同侧时,;
如图②,当点、在的异侧时,
第8课时
线段、角的轴对称性(3)
1.A
2.
4
3.连接、
∵点在的垂直平分线上
∴
∵
∴
在和中
∴
∴点在的平分线上,即平分.
第9课时
线段、角的轴对称性(4)
1.B
2.
①③④⑤
3.如图.在中,,边的垂直平分线交的外角的平分线于点,垂足为,垂足为.求证:
.
3.过点作,垂足为,连接、.
∵
∴
∵平分
∴
在和中,
∴
∴
∵是边的垂直平分线
∴
∵
∴
在和中
∴
∴
∵
∴
第10课时
等腰三角形的轴对称性(1)
1.A
2.
52.5°
3.设
∵
∴
∵的内角和为180°
∴
同理可求
∵在中,
∴
即
整理,得
∵的内角和为180°
第11课时
等腰三角形的轴对称性(1)—习题课
1.D
2.
15°或30°或75°或120°
3.分三种情况讨论:
①当顶角为锐角时,如图①.
∵垂直平分
∴
∵
∴在中,
∵
∴
②当顶角为直角时,,此时,不合题意,舍去.
③当顶角为钝角时,如图②.
∵垂直平分
∴
∵
∴在中,
∵
∴
∵
∴
综上所述,的度数为或
第12课时
等腰三角形的轴对称性(2)
1.D
2.
50°或80°或65°
2.在中,,当的度数为
时,为等腰三角形.
3.
(1)图中有5个等腰三角形:、、、、
与、之间的数量关系是
理由:∵平分
∴
∵
∴
∴
∴
同理可证
∴
(2)若,则图中仍旧存在2个等腰三角形:和,与、之间的数量关系是仍旧存在.
(3)图中存在等腰三角形和,与、之间的数量关系是
理由:∵平分
∴
∵
∴
∴
∴
同理可证
∴
第13课时
等腰三角形的轴对称性(2)—习题课
1.D
2.
3.
(1)如图,∵,都是等边三角形
∴
∵
∴
在和中
∴
∴
(2)如图,由(1),知
∴
∵与的内角和均为180°,且
∴
∵
∴
(3)如图,∵,
∴
在和中
∴
∴
又
∴为等边三角形
∴
∴
∴
第14课时
等腰三角形的轴对称性(3)
1.D
2.
10°
3.
证明:
∵在中,
∴
∵,为的中点
∴
∴
∴
∵,为的中点
∴
∴
∴
∴
又∵,
∴
∴
∵的内角和为180°
∴
∴
轴对称图形
第1课时
轴对称与轴对称图形
1.下列图形中,对称轴的数量小于3的是(
)
2.已知各边相等,各角也相等的多边形叫做正多边形,也称为正边形(这里且为整数).如图,请你探究下列正多边形的对称轴的条数,并填在表格中.
正多边形的边教
3
4
5
6
7
8
对称轴的条数
(1)猜想:正边形有
条对称轴;
(2)当越来越大时,正多边形接近于
,该图形有
条对称轴.
3.小明学习了轴对称知识后,忽然想起了参加数学兴趣小组时老师布置的一道题,当时小明没做出来,题目是这样的:有一组数据排列成方阵,如图.试用简便方法计算这组数据的和.小明想:不考虑每个数据的大小,只考虑每个数据的位置,这个图形是个轴对称图形,能不能用轴对称思想来解决这个问题呢 小明顺着这个思路很快解决了这个题目,请你写出他的解题过程.
第2课时
轴对称的性质(1)
1.如图,把一张长方形纸片沿折叠后,点落在边上的点处,点落在点处,若,则的度数为(
)
A.
115°
B.
120°
C.
130°
D.
140°
2.如图,点关于的对称点分别是,分别交于点,=16
cm,则的周长为
cm.
3.如图,为内部一点,
.
(1)分别画出点关于直线的对称点;
(2)请指出当的度数为多少时,=7,并说明理由;
(3)请判断当的度数不是(2)中的度数时,的长度是小于7还是大于7,并说明你的判断的理由.
第3课时
轴对称的性质(2)
1.如图,点在方格纸的格点位置上,若要再找一个格点,使它们所构成的三角形为轴对称图形,则这样的格点在图中共有(
)
A.
4个
B.
6个
C.
8个
D.
10个
2.如图,在2×2的正方形网格纸中,有一个以格点为顶点的.请你找出网格纸中所有与成轴对称且也以格点为顶点的三角形,这样的不角形共有
个.
3.如图,在由边长为1的正方形组成的6×5方格中,点都在格点上.
(1)在给定的方格中将线段平移到,使得四边形是长方形,且点都落在格点上.画出四边形,并叙述线段的平移过程.
(2)在方格中画出关于直线对称的.
(3)求五边形的面积.
第4课时
轴对称的性质—习题课
7.如图,线段在直线的一侧,请在直线上找一点,使的周长最短.画出图形,保留画图痕迹,不写画法.
2.如图,在直线上找一点,使得与直线的夹角相等.画出图形,保留画图痕迹,不写画法.
3.
(1)如图①,
是内一点,在上分别找点,使得的周长最短.画出图形,保留画图痕迹,不写画法.
(2)如图②,
是内的两点,在上分别找点,使得以为顶点的四边形的周长最短.画出图形,保留画图痕迹,不写画法.
第5课时
设计轴对称图案
1.在一次数学活动课上,小颖将一个四边形纸片依次按如图①②所示的方式对折,然后按图③中的虚线裁剪成图④样式,将纸片展开铺平,所得到的图形是(
)
2.在4×4的方格中,有五个同样大小的正方形按如图所示的方式摆放,移动其中一个正方形到空白方格中,与其余四个正方形组成的新图形是一个轴对称图形,这样的移法共有
种.
3.在3×3的正方形网格图中,有格点三角形和格点三角形,且和
关于某条直线成轴对称,请在如图①~⑥所示的网格中画出六个这样的.(每种方案均不相同)
第6课时
线段、角的轴对称性(1)
1.如图,在中,的垂直平分线分别交于点=
4
,
的周长为23,则的周长为(
)
A.
13
B.
15
C.
17
D.
19
2.如图,在中,的垂直平分线分别交于点的垂直平分线分别交于点.若的周长为2018,则线段的长为
.
3.如图,在中,的垂直平分线交于点,交于点为线段的中点,且.求证:
.
第7课时
线段、角的轴对称性(2)
1.设是内一点,满足,则是
(
)
A.三条内角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
2.如图,在中,边上的垂直平分线交边于点,交边于点.若的周长为24,
与四边形的周长之差为12,则线段的长为
.
3.在中,为平面上一点,且.点到的距离为8,点到的距离为3.求的长.
第8课时
线段、角的轴对称性(3)
1.如图,的面积为6,=3,现将沿所在直线翻折,使点落在直线
上的点处,为直线上的一点,则线段的长不可能是(
)
A.
3
B.
4
C.
5.
5
D.
10
2.如图,分别平分过点,且与垂直.若=8,则点到的距离为
.
3.如图,为的边的垂直平分线,过点作另外两边所在直线的垂线,垂足分别为,且,作射线.求证:
平分.
第9课时
线段、角的轴对称性(4)
1.如图,的平分线交于点,过点作,垂足分别为.下列结论:①平分;②;③;④.其中正确的是(
)
A.
①②③
B.
①③④
C.
②③④
D.①③
2.如图,是的角平分线,分别是和的高,连接,交
于点.下列结论:①;②;③;④;
⑤垂直平分.其中一定正确的是
.(填序号)
3.如图.在中,,边的垂直平分线交的外角的平分线于点,垂足为,垂足为.求证:
.
第10课时
等腰三角形的轴对称性(1)
1.如图,在中,,分别以点和点为圆心,大于的长为半径画弧,两弧相交于点,作直线,交于点,连接,则的度数为(
)
A.
65°
B.
60°
C.
55°
D.
45°
2.如图,在中,为上一点,为上一点,且,则的度数为
.
3.如图,在中,,
为斜边上的两点,且,求的度数.
第11课时
等腰三角形的轴对称性(1)—习题课
1.已知等腰三角形一腰上的高与另一腰的夹角为60°,则这个等腰三角形的底角的度数为(
)
A.
30°
B.
75°
C.
15°或30°
D.
75°或15°
2.如图,在中,,,在边所在的直线上找一点,使是等腰三角形,此时的度数为
.
3.在中,的垂直平分线与所在的直线相交所成的锐角为40°,求的度数.
第12课时
等腰三角形的轴对称性(2)
1.如图,在中,分别是的平分线,且相交于点,则图中的等腰三角形有(
)
A.
5个
B.
6个
C.
7个
D.
8个
2.在中,,当的度数为
时,为等腰三角形.
3.如图①,在中,的平分线交于点,过点作
交于点.
(1)图中有几个等腰三角形 猜想与之间有怎样的数量关系,并说明理由.
(2)如图②,若,其他条件不变,则图中还有等腰三角形吗 如果有,分别写出来;另外在(1)中与之间的数量关系还存在吗
(3)如图③,若在中,
的平分线与的外角平分线交于点,过点作交于点、交于点.这时图中还有等腰三角形吗 与之间的数量关系又如何 并说明你的理由.
第13课时
等腰三角形的轴对称性(2)—习题课
1.如图,,平分,且
=
2.若点分别在上,且为等边三角形,则满足上述条件的有(
)
A.
1个
B.
2个
C.
3个
D.
3个以上
2.如图,在等边三角形中,相交于点于点,则线段的数量关系为
.
3.如图,为线段上一点,,是等边三角形.相交于点交于点,
交于点,连接.
(1)求证:
;
(2)求的度数;
(3)求证:
.
第14课时
等腰三角形的轴对称性(3)
1.如图,在中,
,垂足分别为.若是的中点,则图中等腰三角形有(
)
A.
1个
B.
3个
C.
4个
D.
5个
2.如图,在四边形中,
,
相交于点分别是的中点.如果,那么的度数为
.
3.如图,在中,,点在边上(不与点重合),
于点,连接为的中点.试猜想与的关系并证明.
第2章
轴对称图形
第1课时
轴对称与轴对称图形
1.D
2.
3
4
5
6
7
8
(1)
(2)圆
无数
3.
从方阵的数据看出,正方形的一条对角线上的数据都是10.若把这条对角线所在的直线作为对称轴,把这个方阵对折,对称轴两侧重合的小正方形内的数据之和都是10,相加后如图所示,这样方阵中的所有数据之和为
第2课时
轴对称的性质(1)
1.A
2.
16
3.
(1)如图,过点画,垂足为,在垂线段的延长线上取一点,使得P,此时点就是点关于直线的对称点,同理画出点.
(2)当时,
理由:如图,连接、
∵点、关于直线对称
∴直线垂直平分
∴,
∵
∴
∴,
同理,
∴
若,则,此时、、三点共线
∴
∴
(3)当时,
理由:∵
∴、、三点不在同一直线上,此时构成
∴.由(2),得
∴
第3课时
轴对称的性质(2)
1.D
2.
5
3.(1)如图,将线段先向右平移1个单位长,再向上平移2个单位长度,得线段(平移过程不唯一).
(2)如图,画点关于直线的对称点,连接、,则即为所求.
(
3)
第4课时
轴对称的性质—习题课
1.
由干线段的长度是固定的,要使的周长最短,只要最短即可.如图,过点作它关于直线的对称点,连接交直线于点,连接、,此时就是周长最短的三角形,∴点即为所求.
2.如图,过点作它关干直线的对称点,连接交直线于点.连接、,此时,∴点即为所求.
3.
(1)如图①,过点分别作关于射线、的对称点、,连接,分别交、于点、,连接、、,此时的周长最短,∴点、和即为所求.
(2)如图②.过点、分别作射线、的对称点、,连接,分别交、于点、,连接、、、,此时四边形的周长最短,∴点、和四边形即为所求.
第5课时
设计轴对称图案
1.A
2.
13
3.要使和于某条直线成轴对称,关键是确定适当的对称轴.再根据轴对称的性质画出符合条件的图案,可以以的正方形网格图的对称轴为对称轴画出所求的,有四个不同位置的三角形;也可以以的边、的中点连线所在的直线为对称轴画出所求的,有一个三角形;还可以把过的顶点与边平行的直线作为对称轴画出所求的,也有一个三角形.如图①~⑥中的即为所求
第6课时
线段、角的轴对称性(1)
1.B
2.
2018
3.
连接,
∵是的垂直平分线
∴
∵在中.,,
∴
即
∵为线段的中点
∴
∴垂直平分
∴
∴
第7课时
线段、角的轴对称性(2)
1.D
2.
6
3.∵
∴点在线段的垂直平分线上
∵
∴点也在线段的垂直平分线上
∴所在的直线即为线段的垂直平分线.
设直线与交于点.由题意,得
如图①.当点、在的同侧时,;
如图②,当点、在的异侧时,
第8课时
线段、角的轴对称性(3)
1.A
2.
4
3.连接、
∵点在的垂直平分线上
∴
∵
∴
在和中
∴
∴点在的平分线上,即平分.
第9课时
线段、角的轴对称性(4)
1.B
2.
①③④⑤
3.如图.在中,,边的垂直平分线交的外角的平分线于点,垂足为,垂足为.求证:
.
3.过点作,垂足为,连接、.
∵
∴
∵平分
∴
在和中,
∴
∴
∵是边的垂直平分线
∴
∵
∴
在和中
∴
∴
∵
∴
第10课时
等腰三角形的轴对称性(1)
1.A
2.
52.5°
3.设
∵
∴
∵的内角和为180°
∴
同理可求
∵在中,
∴
即
整理,得
∵的内角和为180°
第11课时
等腰三角形的轴对称性(1)—习题课
1.D
2.
15°或30°或75°或120°
3.分三种情况讨论:
①当顶角为锐角时,如图①.
∵垂直平分
∴
∵
∴在中,
∵
∴
②当顶角为直角时,,此时,不合题意,舍去.
③当顶角为钝角时,如图②.
∵垂直平分
∴
∵
∴在中,
∵
∴
∵
∴
综上所述,的度数为或
第12课时
等腰三角形的轴对称性(2)
1.D
2.
50°或80°或65°
2.在中,,当的度数为
时,为等腰三角形.
3.
(1)图中有5个等腰三角形:、、、、
与、之间的数量关系是
理由:∵平分
∴
∵
∴
∴
∴
同理可证
∴
(2)若,则图中仍旧存在2个等腰三角形:和,与、之间的数量关系是仍旧存在.
(3)图中存在等腰三角形和,与、之间的数量关系是
理由:∵平分
∴
∵
∴
∴
∴
同理可证
∴
第13课时
等腰三角形的轴对称性(2)—习题课
1.D
2.
3.
(1)如图,∵,都是等边三角形
∴
∵
∴
在和中
∴
∴
(2)如图,由(1),知
∴
∵与的内角和均为180°,且
∴
∵
∴
(3)如图,∵,
∴
在和中
∴
∴
又
∴为等边三角形
∴
∴
∴
第14课时
等腰三角形的轴对称性(3)
1.D
2.
10°
3.
证明:
∵在中,
∴
∵,为的中点
∴
∴
∴
∵,为的中点
∴
∴
∴
∴
又∵,
∴
∴
∵的内角和为180°
∴
∴
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
