2017-2018学年沪科版七年级数学上册2.2整式加减 课件
文档属性
| 名称 | 2017-2018学年沪科版七年级数学上册2.2整式加减 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-28 00:00:00 | ||
图片预览











文档简介
课件39张PPT。合并同类项知识回顾举例说明
1.什么叫单项式?
2.什么叫多项式?
3.什么叫整式? 问题2:你认为在上面这个多项式中, 哪些项可以归为一类?问题1:上面的多项式都有哪些项? -4xy2 2xy23x2y 5x2y -3 5归为同一类的项有什么共同特征?创设情境,引入新知 -4xy2 2xy2(3x2y 5x2y)我们把具有如此特征的项称为同类项在多项式中,所含字母相同相同字母的指数也相同所有的常数项也看做同类项同类项,同类项,除了系数都一样归为同一类的项有什么共同特征?自主预习 注意:
1.两个条件缺一不可 ;
2.同类项与系数无关,与字母的排列顺序也无关; 如 - 2xy、5xy与yx
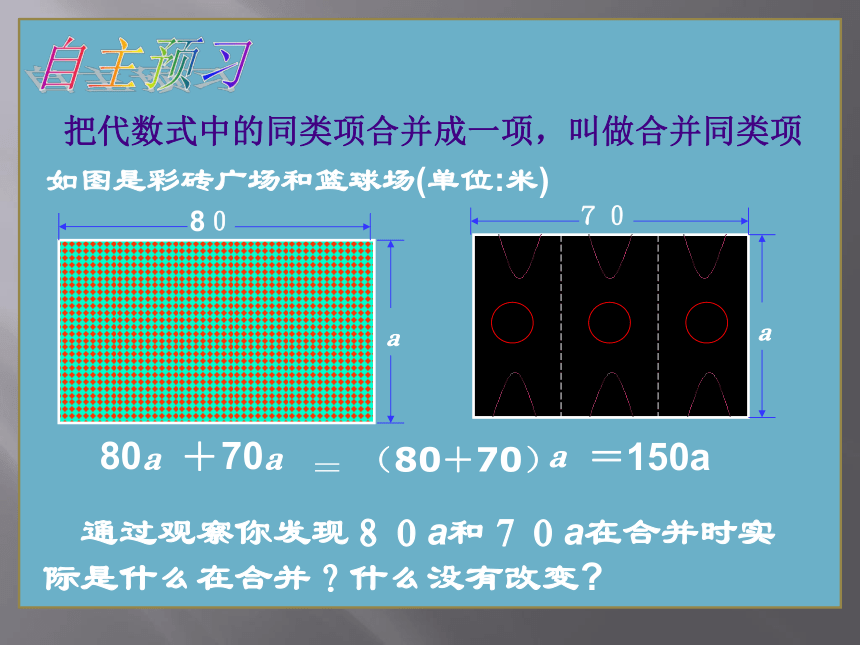
3.所有的常数项都是同类项,如1和-3.如图是彩砖广场和篮球场(单位:米)a=150a 把代数式中的同类项合并成一项,叫做合并同类项 通过观察你发现80a和70a在合并时实际是什么在合并?什么没有改变?(80+70)=自主预习合并同类项的法则: 把同类项的系数_____ , 字母和字母的___________.不要记错呀!简记为:(一加,两不变)
相加指数不变新知运用:
例1.合并下式中的同类项:
4a2+3b2-2ab-3a2+b2自主预习例2:
求多项式3a+abc- c2-3a+ c2的值,其
中a=- ,b=2, c= -3.同 类 项合并同类项自主探究2.完成作业本课本P76第1、2题。 有这样一道题:
当a=0.35,b=-0.28时,求多项式的值:
a3b+2a3-2a2b+3a3b+2a2b-2a3 -4a3b
有一位同学指出:题目中给出的条件a=0.35,b=-0.28是多余的.
他的说法有没有道理?自主探究 判断下列说法是否正确,正确的
在括号内打“√”,错误的打“×”
(1) 与 是同类项( )
(2) 与 是同类项( )
(3) 与 是同类项( )
(4) 与 是同类项( )
(5) 与 是同类项( )随堂练习(1)如果关于字母x的代数式
-3x2 +ax+bx2 +2 x+3合并后不含x的一次项,则下列说法正确的是( ) A. a+b=0 B. a=0C. b=3 D. a=-24D随堂练习(1)本节课学了哪些主要内容?
(2)你能举例说明同类项的概念吗?
(3)举例说明合并同类项的方法.
(4)本节课主要运用了什么思想方法研究问题?知识梳理去括号、添括号知识回顾1.加法的运算定律
2.乘法的运算定律 问题1
图书馆内起初有a名同学,后来了b位同学,1小时后,又来了c位同学,则图书馆内一共有多少位同学。
问题2
若图书馆内原有a名同学.后来有些同学因上课要离开,第一批走了b位同学,第二批又走了c位同学.创设情境,引入新知由问题1得:a+(b+c)=a+b+c
由问题2得:a-(b+c)=a-b-c
问:随着括号的变化,符号有什么变化规律?
再举几个具体数字试试看,概括出去括号法则.1.去括号法则:
(1)如果括号前面是“+”号,去括号时括号里的各项都不改变符号;
(2)如果括号前面是“-”号,去括号时括号里的各项都改变符号;自主预习举例: 例.去括号,再合并同类项。 (1). 4a-(a-3b) (2). a+(5a-3b)-(a-2b) (3). 3(2xy-y)-2xy解:(1) 4a-(a-3b) =4a-a+3b (去括号法则) =3a+3b (合并同类项法则)(2) a+(5a-3b)-(a-2b) =a+5a-3b-a+2b (去括号法则) =5a-b (合并同类项法则) (3) 3(2xy-y)-2xy = (6xy-3y)-2xy (乘法分配律) =6xy-3y-2xy (去括号法则) =4xy-3y (合并同类项法则)例 先去括号,再合并同类项:
(1)8a+2b+(5a-2b)
(2)a+(5a-3b)-2(a-2b) 用式子表示十位上的数是a,个位上的数是b的两位数,再把这个两位数的十位上的数与个位上的数交换位置,计算所得数与原数的和,所得数与原数的和能被11整除吗?解:原来的两位数为10a+b,
新的两位数为10b+a
两个数的和为10a+b+10b+a
=11a+11b
=11(a+b)∴所得数与原数的和能被11整除.自主探究练习1;下列去括号对不对?若不对,请指出错在哪里应怎样改正?
( ) (1) - ( x – 6 ) = - x – 6
( )(2)3a – ( 5b – 2c + 1) = 3a–5b +–1
( )(3) x + 3 ( y – w ) = x + 3y – w
( )(4)x – 2 (– y + g ) = x + 2y + g
( )(5) –( a–2b )+(c–2 ) = - a–2b+c– 2
( ) (6) - a + b = - ( b + a )
( ) (7) 2 + 3 x = - ( 3 x – 2 )
√××××√×随堂练习练习2:去括号,并合并同类项:
( 1)8x-(-3x-5)
( 2 ) a-(5a-3b)+(2b-a)
( 3 ) 3x+1-2(4-x)
( 4 ) –0.5(2x+y)+0.25(4p+q)
(4).求(2x2 -3xy+y2-2xy)-(2x2 -5xy+2y-1)
的值,其中练习3这节课你有什么收获呢?小结:知识梳理(1)如果括号前面是“+”号,去括号时括号里的各项都不改变符号;
(2)如果括号前面是“-”号,去括号时括号里的各项都改变符号;整式的加减知识回顾1.整式加减的步骤有哪些?
2.去括号、添括号的法则。
3.整式的加减运算可以归纳为___和______.创设情境,引入新知1.思考:去括号要注意什么?
并同类项要注意什么?
2.尝试完成
例4. 求整式4-5x2+3x与-2x+7x2-3的和自主预习1.什么叫升幂排列?降幂排列?
2.例5 先化简,再求值。
5a2-〔a2-(2a-5a2)-2(a2-3a)〕,
其中a=4.
解答过程中注意什么?为什么要先化简再求值?
注意:求两个代数式的差时,一定要加括号!!! =2a2-4a+1+3a2-2a+5=5a2-6a+6?解: (2a2-4a+1)-(-3a2+2a-5)求2a2-4a+1 与-3a2+2a-5的差自主探究 2. 求 的值
其中 x=-2, y= 时.→去括号→合并同类项﹜﹜将式子化简再代入数值进行
计算3. 两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是50千米/时,水流速度是a千米/时。
(1)2小时后两船相距多远?
(2)2小时后甲船比乙船多航行多少千米?探究:
顺水航速=船速+水速=______
逆水航速=船速-水速=_______(1) 2小时后两船向距:
(2) 2小时后甲船比乙船多航行:
解:(1) 2小时后两船向距:
2(50+a)+2(50-a)
=100+2a+100-2a
=200(km)
(2) 2小时后甲船比乙船多航行:
2(50+a)-2(50-a)
=100+2a-100+2a
=4a(km) 1.整式的加减运算法则 。
2.升幂排列、降幂排列。
3.比较复杂的式子求值,先化简,再把数值
代入计算。
知识梳理 1. 2x +x+1与A的和是x,则A=( )
A。2x +1 B -2X +1 C 2x -1 D -2X -122222D2.已知a+2b=5,ab=-3,则(3ab-2b)+(4b-4ab+a)=_______.
3.先化简,再求值。
-2-(2a-3b+1)-(3a+2b),其中a=-3 ,b=-2.8随堂练习4.一种笔记本的单价是x 元,圆珠笔的单价是y元,小红买这种笔记本3个,买圆珠笔2支;小明买这种笔记本4个,买圆珠笔3支。买这些笔记本和圆珠笔,小红和小明一共花费多少钱?解法一:小红买笔记本和圆珠笔共花费_________元,小明买笔记本和圆珠笔共花费________元。
小红和小明一共花费________________________.解法二:小红和小明买笔记本共花费___________元,买圆珠笔共花费__________元。小红和小明一共花小红和小明一共花费_____________________.
学习和研究好比爬梯子,要一步一步地往上爬,企图一脚跨上四五步,平地登天,那就必须会摔跤了。
————?华罗庚
结束语
1.什么叫单项式?
2.什么叫多项式?
3.什么叫整式? 问题2:你认为在上面这个多项式中, 哪些项可以归为一类?问题1:上面的多项式都有哪些项? -4xy2 2xy23x2y 5x2y -3 5归为同一类的项有什么共同特征?创设情境,引入新知 -4xy2 2xy2(3x2y 5x2y)我们把具有如此特征的项称为同类项在多项式中,所含字母相同相同字母的指数也相同所有的常数项也看做同类项同类项,同类项,除了系数都一样归为同一类的项有什么共同特征?自主预习 注意:
1.两个条件缺一不可 ;
2.同类项与系数无关,与字母的排列顺序也无关; 如 - 2xy、5xy与yx
3.所有的常数项都是同类项,如1和-3.如图是彩砖广场和篮球场(单位:米)a=150a 把代数式中的同类项合并成一项,叫做合并同类项 通过观察你发现80a和70a在合并时实际是什么在合并?什么没有改变?(80+70)=自主预习合并同类项的法则: 把同类项的系数_____ , 字母和字母的___________.不要记错呀!简记为:(一加,两不变)
相加指数不变新知运用:
例1.合并下式中的同类项:
4a2+3b2-2ab-3a2+b2自主预习例2:
求多项式3a+abc- c2-3a+ c2的值,其
中a=- ,b=2, c= -3.同 类 项合并同类项自主探究2.完成作业本课本P76第1、2题。 有这样一道题:
当a=0.35,b=-0.28时,求多项式的值:
a3b+2a3-2a2b+3a3b+2a2b-2a3 -4a3b
有一位同学指出:题目中给出的条件a=0.35,b=-0.28是多余的.
他的说法有没有道理?自主探究 判断下列说法是否正确,正确的
在括号内打“√”,错误的打“×”
(1) 与 是同类项( )
(2) 与 是同类项( )
(3) 与 是同类项( )
(4) 与 是同类项( )
(5) 与 是同类项( )随堂练习(1)如果关于字母x的代数式
-3x2 +ax+bx2 +2 x+3合并后不含x的一次项,则下列说法正确的是( ) A. a+b=0 B. a=0C. b=3 D. a=-24D随堂练习(1)本节课学了哪些主要内容?
(2)你能举例说明同类项的概念吗?
(3)举例说明合并同类项的方法.
(4)本节课主要运用了什么思想方法研究问题?知识梳理去括号、添括号知识回顾1.加法的运算定律
2.乘法的运算定律 问题1
图书馆内起初有a名同学,后来了b位同学,1小时后,又来了c位同学,则图书馆内一共有多少位同学。
问题2
若图书馆内原有a名同学.后来有些同学因上课要离开,第一批走了b位同学,第二批又走了c位同学.创设情境,引入新知由问题1得:a+(b+c)=a+b+c
由问题2得:a-(b+c)=a-b-c
问:随着括号的变化,符号有什么变化规律?
再举几个具体数字试试看,概括出去括号法则.1.去括号法则:
(1)如果括号前面是“+”号,去括号时括号里的各项都不改变符号;
(2)如果括号前面是“-”号,去括号时括号里的各项都改变符号;自主预习举例: 例.去括号,再合并同类项。 (1). 4a-(a-3b) (2). a+(5a-3b)-(a-2b) (3). 3(2xy-y)-2xy解:(1) 4a-(a-3b) =4a-a+3b (去括号法则) =3a+3b (合并同类项法则)(2) a+(5a-3b)-(a-2b) =a+5a-3b-a+2b (去括号法则) =5a-b (合并同类项法则) (3) 3(2xy-y)-2xy = (6xy-3y)-2xy (乘法分配律) =6xy-3y-2xy (去括号法则) =4xy-3y (合并同类项法则)例 先去括号,再合并同类项:
(1)8a+2b+(5a-2b)
(2)a+(5a-3b)-2(a-2b) 用式子表示十位上的数是a,个位上的数是b的两位数,再把这个两位数的十位上的数与个位上的数交换位置,计算所得数与原数的和,所得数与原数的和能被11整除吗?解:原来的两位数为10a+b,
新的两位数为10b+a
两个数的和为10a+b+10b+a
=11a+11b
=11(a+b)∴所得数与原数的和能被11整除.自主探究练习1;下列去括号对不对?若不对,请指出错在哪里应怎样改正?
( ) (1) - ( x – 6 ) = - x – 6
( )(2)3a – ( 5b – 2c + 1) = 3a–5b +–1
( )(3) x + 3 ( y – w ) = x + 3y – w
( )(4)x – 2 (– y + g ) = x + 2y + g
( )(5) –( a–2b )+(c–2 ) = - a–2b+c– 2
( ) (6) - a + b = - ( b + a )
( ) (7) 2 + 3 x = - ( 3 x – 2 )
√××××√×随堂练习练习2:去括号,并合并同类项:
( 1)8x-(-3x-5)
( 2 ) a-(5a-3b)+(2b-a)
( 3 ) 3x+1-2(4-x)
( 4 ) –0.5(2x+y)+0.25(4p+q)
(4).求(2x2 -3xy+y2-2xy)-(2x2 -5xy+2y-1)
的值,其中练习3这节课你有什么收获呢?小结:知识梳理(1)如果括号前面是“+”号,去括号时括号里的各项都不改变符号;
(2)如果括号前面是“-”号,去括号时括号里的各项都改变符号;整式的加减知识回顾1.整式加减的步骤有哪些?
2.去括号、添括号的法则。
3.整式的加减运算可以归纳为___和______.创设情境,引入新知1.思考:去括号要注意什么?
并同类项要注意什么?
2.尝试完成
例4. 求整式4-5x2+3x与-2x+7x2-3的和自主预习1.什么叫升幂排列?降幂排列?
2.例5 先化简,再求值。
5a2-〔a2-(2a-5a2)-2(a2-3a)〕,
其中a=4.
解答过程中注意什么?为什么要先化简再求值?
注意:求两个代数式的差时,一定要加括号!!! =2a2-4a+1+3a2-2a+5=5a2-6a+6?解: (2a2-4a+1)-(-3a2+2a-5)求2a2-4a+1 与-3a2+2a-5的差自主探究 2. 求 的值
其中 x=-2, y= 时.→去括号→合并同类项﹜﹜将式子化简再代入数值进行
计算3. 两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是50千米/时,水流速度是a千米/时。
(1)2小时后两船相距多远?
(2)2小时后甲船比乙船多航行多少千米?探究:
顺水航速=船速+水速=______
逆水航速=船速-水速=_______(1) 2小时后两船向距:
(2) 2小时后甲船比乙船多航行:
解:(1) 2小时后两船向距:
2(50+a)+2(50-a)
=100+2a+100-2a
=200(km)
(2) 2小时后甲船比乙船多航行:
2(50+a)-2(50-a)
=100+2a-100+2a
=4a(km) 1.整式的加减运算法则 。
2.升幂排列、降幂排列。
3.比较复杂的式子求值,先化简,再把数值
代入计算。
知识梳理 1. 2x +x+1与A的和是x,则A=( )
A。2x +1 B -2X +1 C 2x -1 D -2X -122222D2.已知a+2b=5,ab=-3,则(3ab-2b)+(4b-4ab+a)=_______.
3.先化简,再求值。
-2-(2a-3b+1)-(3a+2b),其中a=-3 ,b=-2.8随堂练习4.一种笔记本的单价是x 元,圆珠笔的单价是y元,小红买这种笔记本3个,买圆珠笔2支;小明买这种笔记本4个,买圆珠笔3支。买这些笔记本和圆珠笔,小红和小明一共花费多少钱?解法一:小红买笔记本和圆珠笔共花费_________元,小明买笔记本和圆珠笔共花费________元。
小红和小明一共花费________________________.解法二:小红和小明买笔记本共花费___________元,买圆珠笔共花费__________元。小红和小明一共花小红和小明一共花费_____________________.
学习和研究好比爬梯子,要一步一步地往上爬,企图一脚跨上四五步,平地登天,那就必须会摔跤了。
————?华罗庚
结束语
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
