2017-2018学年湘教版七年级数学上册课件1.2 数轴、相反数与绝对值(42张PPT)
文档属性
| 名称 | 2017-2018学年湘教版七年级数学上册课件1.2 数轴、相反数与绝对值(42张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 911.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-09-29 07:21:31 | ||
图片预览








文档简介
课件42张PPT。
1.2.1 数轴1℃℃℃50-10观 察 周 围 的 生 活例 1例 2O-1公里1公里2.6公里家外婆家公园学校O-1公里1公里2.6公里家外婆家公园学校O-1公里1公里2.6公里家外婆家公园学校 由例1中带有刻度的温度表和例2中带有公里数的笔直的马路,由此联想,我们是否可以用一条直线上的一些点表示有理数?赶快思考啊!!!从上面的例子受到启发,我们可以用一条直线上的点来直观地表示数.
1、画一条水平放置的直线,在直线上取一点0,把点叫作原点(origin).
2、规定直线上向右的方向为正方向,
3、选取适当的长度作为单位长度,就得到了数轴.如下图所示
总结:这样规定了原点、单位长度和正方向的直线叫作数轴(number axis).如下图表示.
由上可知,任何有理数都可以用数轴上唯一的一个点来表示.
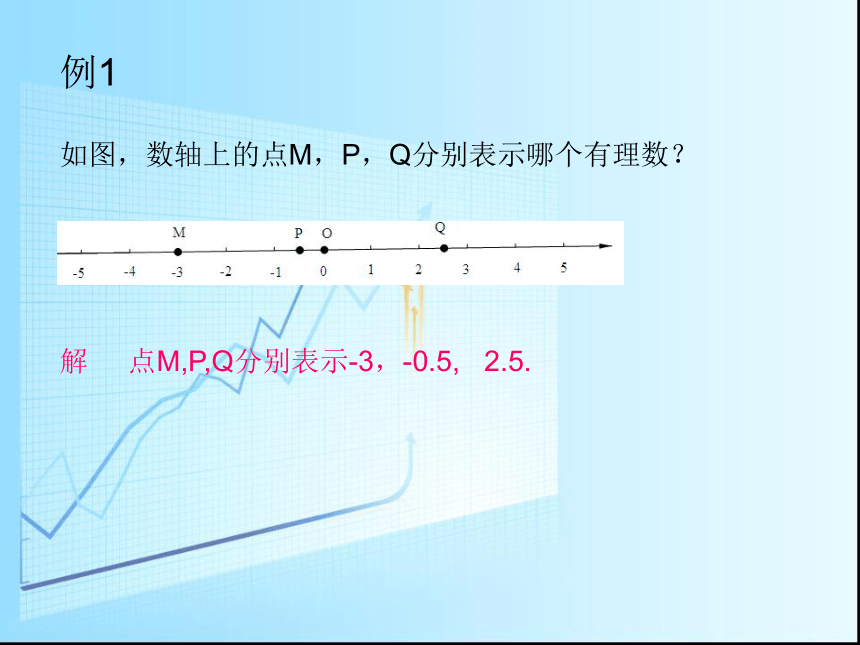
例1如图,数轴上的点M,P,Q分别表示哪个有理数?
解 点M,P,Q分别表示-3,-0.5, 2.5.例2:画一条数轴,并标出表示下列个数的点:
解 所画数轴及各数在数轴上对应的点如图所示.1.填空:
数轴上表示-2的点在原点的 侧,距原
点的距离是 ,表示6的点在原点
的 侧,距原点的距离是 .2.判断:
数轴上的两个点可以表示同一个有理数( )6个单位左右2个单位╳练习:3.下列命题正确的是( )
A:数轴上的点都表示整数
B:数轴上表示5与-5的点分别在原点的
两侧,并且到原点的距离都等于5个
单位长度
C:数轴包括原点与正方向两个要素
D:数轴上的点只能表示正数和零B4.自己画一条数轴,并在数周上表示下列各数的点:-2,
-0.8,0.8,230.82-2 0-0.8思考题:
(1).一个点在数轴上表示的数是-5,这个点先向左边移动3个单位,然后再向右边移动6个单位,这时它表示的数是多少呢?
答:它表示的数是-2. (2).如果按上面的移动规律,最后得到的点表 示的数是2,则开始时它表示什么数?答:开始它表示-1.
正方向数轴的三要素单位长度原点布置作业 数轴的引入,使我们能用直观图形来理解数的有关概念,这就是“数”与“形”的结合,数形结合是一种重要的方法,我们应注意掌握.课堂小结: 1.2.2 相反数1仔细观察:-3-2-10123AB在下图中,数轴上点A和点B表示的数有什么关系?赶快思考啊!!! 点A表示3,点B表示-3,
他们只有符号不同.点A与原点的距离是3,
点B与原点的距离也是3,
他们距离原点的距离是一样的.
总结: 像3和-3那样,如果两个数只有符号不同,那么其中的一个数叫作另一个数的相反数(opposite number),或者说他们互为相反数. 例如,3的相反数是-3,-3的相反数是3,我们把数a的相反数记作-a,于是“-3的相反数是3”就可以记作“-(-2.6)=2.6 ” 即 “ –(-a)=a”. (1)0的相反数是0;
(2)表示互为相反数的两个数的点,在数轴上分别位于 原点的两侧,并且与原点的距离相等.
补充:你明白了吗?例1:画一条数轴,并标出表示下列各数的相反数的点:
3, 1.5, -6.
解 3的相反数是-3;1.5的相反数是-1.5;-6的相反数是6,且-3,-1.5,6在数轴上对应的点分别为A,B,C,如图所示:例2:填空:-(+0.8)=_________;-(-3)=_________.
解 -(+0.8)=-0.8;-(-3)=3.
练 一 练1.填空:
1.3的相反数是 ______ 20的相反数是______
-6的相反数是______ 0的相反数是_______
-(-3)=______ -(9)=_______ -(-0.8)=______-1.3-206300.8-92.选择:
下列几对数中互为相反数的一对为( )
A.-(-8)和-(+8)B.-(+8)与+(-8) C.-(-8)与-(+8)B3.在数轴上标出2,-1, 5,-3及它们的相反数,观察每对相反数所对应的点到原点的距离有什么关系.
解:2的相反数是-2,-1.5的相反数是1.5,-3的相反数是3.它们在数轴上表示如下图所示;
每对相反数所对应的点到原点的距离相等.
课堂小结本节课学习了以下内容:
1.相反数的概念:如果两个数只有符号不同,那么其中一个数叫做另一个数的相反数.
2.-a表示a的相反数.
布置作业: 1.2.3 绝对值01234-1-2-3观察:1 上图中,单位长度为1米,那么大象、两只小狗分别距离原点多远?赶快思考啊!!!聪明的同学们一眼就可以看出来了吧:
大象距离原点4米
两只小狗距离原点3米 一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值(absolute value).
想一想 互为相反数的两个数的绝对值有什么关系?
提示:一对相反数虽然分别在原点两边,但它们到原点的距离是相等的.
想一想 这里的数a可以表示什么样的数?这里的数a可以是正数,负数和0一个数a的绝对值就是数轴上表示数a的点与原点的距离. 一个数的绝对值就是在这个数的两旁各画一条竖线,如+2的绝对值等于2,记作|+2|=2.
数a的绝对值记作|a|. 如图,在数轴上表示-5的点与原点的距离是5,即-5的绝对值是5,记作|-5|=5. 的绝对值是记作议一议 一个数的绝对值与这个数有什么关系?例如:|3|=3,|+7|=7 …………一个正数的绝对值是它本身例如:|-3|=3,|-2.3|=2.3 ………… 一个负数的绝对值是它的相反数0的绝对值是0,即 |0|=0而原点到原点的距离是0例1 求下列各数的绝对值:
127.50做一做写出下列各数的绝对值:
解: 因为正数可用a>0表示,负数可用a<0表示,所以上述三条可表述成: (1)如果a>0,那么|a|=a (2)如果a<0,那么|a|=-a (3)如果a=0,那么|a|=0 a (a>0)0 (a=0)- a (a<0)即:︱a︱=或者:任何一个有理数的绝对值都是非负数.即:例2 若| a |=8.7,求a.
解 因为绝对值等于8.7的有理数有8.7和-8.7
两个,所以a=8.7或a=-8.7.练习: 2.比较大小:│-5│ │-8│;│-0.05│ 0;│-3│ 1.-6 和 +6 ;03. 判断(对的打“√”,错的打“×”):
(1)一个有理数的绝对值一定是正数 ( )(2)-1.4<0,则│-1.4│<0 ( )(3) │-32︱的相反数是32 ( )(4) 如果两个数的绝对值相等,那么这两个数
相等 ( )(5) 互为相反数的两个数的绝对值相等 ( )
0abc则│a│ │c│, │b│ │c│
4. 已知有三个数a,b,c在数轴上的位置如下图所示则a,b,c三个数从小到大的顺序是:c < b < a<<5. 足球比赛中对所用的足球有严格的规定,下面是5个足球的质量检测结果(用正数表示超过规定质量的克数,用负数表示不足规定质量的克数)答:记为-8的足球质量好一些.
因为│-20│=20,│+10│=10,│+12│=12,
│-8│=8,│-11│=11
所以│-8│ < │+10│ < │-11│ < │+12│ < │-20│
也就是说记为-8的足球与规定的质量相差比较小,
因此其质量比较好.-20 +10 +12 -8 -11请指出哪个足球的质量好一些,并用绝对值的知识加以说明.课堂小结一个正数的绝对值等于它本身
一个负数的绝对值等于它的相反数
0的绝对值等于0
互为相反数的两个数的绝对值相等
布置作业:
1、画一条水平放置的直线,在直线上取一点0,把点叫作原点(origin).
2、规定直线上向右的方向为正方向,
3、选取适当的长度作为单位长度,就得到了数轴.如下图所示
总结:这样规定了原点、单位长度和正方向的直线叫作数轴(number axis).如下图表示.
由上可知,任何有理数都可以用数轴上唯一的一个点来表示.
例1如图,数轴上的点M,P,Q分别表示哪个有理数?
解 点M,P,Q分别表示-3,-0.5, 2.5.例2:画一条数轴,并标出表示下列个数的点:
解 所画数轴及各数在数轴上对应的点如图所示.1.填空:
数轴上表示-2的点在原点的 侧,距原
点的距离是 ,表示6的点在原点
的 侧,距原点的距离是 .2.判断:
数轴上的两个点可以表示同一个有理数( )6个单位左右2个单位╳练习:3.下列命题正确的是( )
A:数轴上的点都表示整数
B:数轴上表示5与-5的点分别在原点的
两侧,并且到原点的距离都等于5个
单位长度
C:数轴包括原点与正方向两个要素
D:数轴上的点只能表示正数和零B4.自己画一条数轴,并在数周上表示下列各数的点:-2,
-0.8,0.8,230.82-2 0-0.8思考题:
(1).一个点在数轴上表示的数是-5,这个点先向左边移动3个单位,然后再向右边移动6个单位,这时它表示的数是多少呢?
答:它表示的数是-2. (2).如果按上面的移动规律,最后得到的点表 示的数是2,则开始时它表示什么数?答:开始它表示-1.
正方向数轴的三要素单位长度原点布置作业 数轴的引入,使我们能用直观图形来理解数的有关概念,这就是“数”与“形”的结合,数形结合是一种重要的方法,我们应注意掌握.课堂小结: 1.2.2 相反数1仔细观察:-3-2-10123AB在下图中,数轴上点A和点B表示的数有什么关系?赶快思考啊!!! 点A表示3,点B表示-3,
他们只有符号不同.点A与原点的距离是3,
点B与原点的距离也是3,
他们距离原点的距离是一样的.
总结: 像3和-3那样,如果两个数只有符号不同,那么其中的一个数叫作另一个数的相反数(opposite number),或者说他们互为相反数. 例如,3的相反数是-3,-3的相反数是3,我们把数a的相反数记作-a,于是“-3的相反数是3”就可以记作“-(-2.6)=2.6 ” 即 “ –(-a)=a”. (1)0的相反数是0;
(2)表示互为相反数的两个数的点,在数轴上分别位于 原点的两侧,并且与原点的距离相等.
补充:你明白了吗?例1:画一条数轴,并标出表示下列各数的相反数的点:
3, 1.5, -6.
解 3的相反数是-3;1.5的相反数是-1.5;-6的相反数是6,且-3,-1.5,6在数轴上对应的点分别为A,B,C,如图所示:例2:填空:-(+0.8)=_________;-(-3)=_________.
解 -(+0.8)=-0.8;-(-3)=3.
练 一 练1.填空:
1.3的相反数是 ______ 20的相反数是______
-6的相反数是______ 0的相反数是_______
-(-3)=______ -(9)=_______ -(-0.8)=______-1.3-206300.8-92.选择:
下列几对数中互为相反数的一对为( )
A.-(-8)和-(+8)B.-(+8)与+(-8) C.-(-8)与-(+8)B3.在数轴上标出2,-1, 5,-3及它们的相反数,观察每对相反数所对应的点到原点的距离有什么关系.
解:2的相反数是-2,-1.5的相反数是1.5,-3的相反数是3.它们在数轴上表示如下图所示;
每对相反数所对应的点到原点的距离相等.
课堂小结本节课学习了以下内容:
1.相反数的概念:如果两个数只有符号不同,那么其中一个数叫做另一个数的相反数.
2.-a表示a的相反数.
布置作业: 1.2.3 绝对值01234-1-2-3观察:1 上图中,单位长度为1米,那么大象、两只小狗分别距离原点多远?赶快思考啊!!!聪明的同学们一眼就可以看出来了吧:
大象距离原点4米
两只小狗距离原点3米 一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值(absolute value).
想一想 互为相反数的两个数的绝对值有什么关系?
提示:一对相反数虽然分别在原点两边,但它们到原点的距离是相等的.
想一想 这里的数a可以表示什么样的数?这里的数a可以是正数,负数和0一个数a的绝对值就是数轴上表示数a的点与原点的距离. 一个数的绝对值就是在这个数的两旁各画一条竖线,如+2的绝对值等于2,记作|+2|=2.
数a的绝对值记作|a|. 如图,在数轴上表示-5的点与原点的距离是5,即-5的绝对值是5,记作|-5|=5. 的绝对值是记作议一议 一个数的绝对值与这个数有什么关系?例如:|3|=3,|+7|=7 …………一个正数的绝对值是它本身例如:|-3|=3,|-2.3|=2.3 ………… 一个负数的绝对值是它的相反数0的绝对值是0,即 |0|=0而原点到原点的距离是0例1 求下列各数的绝对值:
127.50做一做写出下列各数的绝对值:
解: 因为正数可用a>0表示,负数可用a<0表示,所以上述三条可表述成: (1)如果a>0,那么|a|=a (2)如果a<0,那么|a|=-a (3)如果a=0,那么|a|=0 a (a>0)0 (a=0)- a (a<0)即:︱a︱=或者:任何一个有理数的绝对值都是非负数.即:例2 若| a |=8.7,求a.
解 因为绝对值等于8.7的有理数有8.7和-8.7
两个,所以a=8.7或a=-8.7.练习: 2.比较大小:│-5│ │-8│;│-0.05│ 0;│-3│ 1.-6 和 +6 ;03. 判断(对的打“√”,错的打“×”):
(1)一个有理数的绝对值一定是正数 ( )(2)-1.4<0,则│-1.4│<0 ( )(3) │-32︱的相反数是32 ( )(4) 如果两个数的绝对值相等,那么这两个数
相等 ( )(5) 互为相反数的两个数的绝对值相等 ( )
0abc则│a│ │c│, │b│ │c│
4. 已知有三个数a,b,c在数轴上的位置如下图所示则a,b,c三个数从小到大的顺序是:c < b < a<<5. 足球比赛中对所用的足球有严格的规定,下面是5个足球的质量检测结果(用正数表示超过规定质量的克数,用负数表示不足规定质量的克数)答:记为-8的足球质量好一些.
因为│-20│=20,│+10│=10,│+12│=12,
│-8│=8,│-11│=11
所以│-8│ < │+10│ < │-11│ < │+12│ < │-20│
也就是说记为-8的足球与规定的质量相差比较小,
因此其质量比较好.-20 +10 +12 -8 -11请指出哪个足球的质量好一些,并用绝对值的知识加以说明.课堂小结一个正数的绝对值等于它本身
一个负数的绝对值等于它的相反数
0的绝对值等于0
互为相反数的两个数的绝对值相等
布置作业:
同课章节目录
